基于深度Q学习策略的旋转机械故障诊断方法研究*

辛 阔,王建国*,张文兴

(1.内蒙古科技大学 机械工程学院,内蒙古 包头 014010;2.内蒙古自治区机电系统智能诊断与控制重点实验室,内蒙古 包头 014010)

0 引 言

随着现代领域生产的发展和科学技术的进步,机械设备的复杂度也大大提高。因此，高效的基于状态的维护(condition-based maintenance,CBM)方法已成为现代机械设备维护的发展趋势[1]。

在工业领域，CBM思想的应用有效地减少了因机械故障所造成的经济损失。机械装备的重要组成部分是轴承和齿轮等部件,而轴承和齿轮对机械设备的工况有比较大的影响,因此，轴承、齿轮的维护成为提高装备使用寿命的关键之一。

近年来,随着人工智能的兴起,有关于机械设备智能诊断方面的研究越来越热。由于能够处理大量数据并且进行辨别,在机械的故障诊断领域,传统机器学习和深度学习有着普遍的应用。这些方法大多包括两个部分:(1)提取故障的特征;(2)对故障状态进行分类。

鄢仁武等人[2]通过对断路器的小波时频图分析,结合卷积神经网络进行了对断路器的故障识别。柳青秀等人[3]提出了一种基于长短时记忆—自编码(LSTM-AE)神经网络的风电机组性能评估及异常检测方法,有效地提高了对风机异常检测的准确性。曹惠玲[4]通过AdaBoost算法及其改进算法的结合,建立了一种多分类的AdaBoost算法,以支持向量机(SVM)为基础分类器,对航空发动机进行了良好的故障诊断。李恒等人[5]利用短时傅里叶变换对振动数据进行了处理,得到了时频谱样本,将其输入卷积神经网络中进行了学习,获得了比较好的识别精度和优良的鲁棒性。吴春志等人[6]利用原始复合故障数据训练了一维卷积神经网络(CNN),使网络有了良好的故障识别效果;并探索了不同卷积核及CNN层数,对网络精度和训练速度的影响。陈仁祥等人[7]提出了一种基于卷积神经网络和离散小波变换的滚动轴承故障诊断方法。

2015年Google DeepMind团队[8]成功将深度学习(DL)和强化学习(RL)结合,并很好地将其应用于游戏控制中,掀起了新一轮强化学习的研究高潮。QIAO Jun-fei等人[9]通过应用深度自编码器提取了图片特征,并使用Q学习策略实现了分类的对手写数字的识别方法,有效增强了准确性,并减少了识别运行时间。MEHRTASH T[10]通过使用强化学习来寻找人脸图像上的特征,从而完成了对人脸的识别。

上述方法虽然都在识别精度上有着良好的表现,但仍存在下列问题:(1)输入信号多为人工经信号处理后的特征向量或图片,这不仅需要比较强的先验知识,而且可能造成对原始信号的破坏;(2)当前所见到的大多数模型未考虑到参杂噪声信号情况下的故障诊断,而在实际生产的复杂环境下难免会有噪声信号,这会大大降低模型的诊断精度和鲁棒性;(3)传统的深度神经网络多存在局部最小值和过拟合等问题,使得模型训练后出现准确率不高且稳定性较差的现象。

为解决上述问题,笔者采用一种端到端的故障诊断方法。该方法使用随机置零策略处理过的振动数据,用于提高模型对不同噪声的鲁棒性;通过训练具有感知能力和决策能力的深度强化学习网络,提高模型对不同噪声环境下的故障识别精度,进而使模型具有良好的抗噪性能。

1 深度强化学习

深度强化学习是将深度学习和强化学习结合的一种通过智能体与环境不断交互的试错算法。深度强化学习使网络既有感知能力又有决策能力,形成了一种更接近人类思维的智能算法。

1.1 卷积神经网络

卷积神经网络是一种模仿生物自然视觉认知机制,一种采用图像卷积计算的深度学习网络框架。典型的CNN主要由:卷积层、池化层和全连接层构成。

卷积层采用矩形卷积核与输入信号的局部感受域进行卷积计算,使用相同数值权重的卷积核对输入数据,并进行扫描,使其参数得到共享。

卷积操作的数学模型为:

g(i)=Wi⊗xi+bi,i=1,2,…,I

(1)

式中:xi—当前的输入特征向量;xi+1—卷积计算后的特征向量;⊗—卷积运算符号;Wi—卷积核的权重;bi—偏置;i—第i个卷积核。

完成卷积操作后,通过激活函数实现非线性变换,以提高模型的表达能力。其表达式为:

yi=f(g(i))，i=1,2,…,I

(2)

式中:yi—激活层输出后的特征;f(·)—激活函数。

卷积运算后特征向量的数量会有较大的增加,虽然可以提高特征提取能力,但同时也会出现维数过大的问题,增加输出的维度。而池化层可以有效地减少参数的数量,池化操作可以有效地保留特征信息,同时降低特征向量的尺寸维度。

CNN中应用最多的是最大池化,其表达式为:

(3)

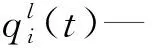
1.2 马尔可夫决策过程

马尔可夫决策过程一般用来描述强化学习任务。马尔可夫决策过程包含四元组,其中:S—状态空间集,s—状态空间集中的一个状态,s∈S;A—动作空间集,a—动作空间集中的一个动作,a∈A;p—动作a被智能体执行后当前时刻状态s转化到下一时刻状态s′的概率;r—动作A被智能体执行后当前时刻状态s转化到下一时刻状态s′所获得的奖励。

马尔可夫决策过程具有马尔可夫属性,即当前时刻下,环境的反馈只取决于上一时刻的状态和动作,与之前更早的时刻没有关联性。

在本文的故障识别任务中,状态s为一维故障信号;动作a为机械故障的类别:0,1,2,…,Y-1,其中:Y—故障类别数量;模型识别结果与故障样本类型是否一致是给予奖励r的重要标准,样本类型与识别结果一致时r取+1,否则r取-1;对于状态转移概率p而言,尽管各个状态之间没有关联,在网络运行时,为避免出现过拟合现象,会任意打乱训练数据样本,且使各个训练数据样本数目均匀分布,状态转移概率也就成为了p=1/Y;且s′只有在动作a被执行后,状态s以概率p转移得到,和前一时刻的状态没有关联,就符合马尔可夫属性。

1.3 策略

强化学习就是为了求解马尔可夫决策过程的最优策略。最优策略可以通过求解最优值函数得到[11],简而言之,强化学习的求解最后演化成了优化贝尔曼方程,其数学模型为:

Rt=rt+rr+1+…+rn
V(st)=E[Rt+γ(Rt+1+γ(Rt+2…))]
V(st)=E[Rt+γV(st+1)]

(4)

式中:γ—折扣系数,是介于[0,1]的常数,γ的存在可以保证模型更容易获取长期累计奖励;Rt—未来累计奖励;r—执行动作后获得的奖励。在训练时,初始化V(s)=0。

上式展示了当前状态值函数V(s)与未来状态值函数V(st+1)的递归关系。显然上式较关注的是状态,但要知道在状态s下,利用某个策略π采用动作a获取的期望回报,就有了Q函数,即:

(5)

当前状态值函数V(s)的表达式为:

V(s)=∑a∈Aπ(a|s)Q(s,a)

(6)

所以,在最优策略下的最优Q函数为:

(7)

(8)

上式经过处理后使用了关于a的指数加权平均[12],即为贝尔曼最优化方程。

在故障诊断任务中,状态空间集S的数量非常大,而有限的空间并不能有效地存储使用状态动作对的Q值。较强的函数泛化能力是深度学习网络的一大特点,可以用于对Q函数进行拟合,记作Q(s,a;θ),其中:θ—神经网络的未知参数。

此处笔者使用了一个权重参数为θ的卷积神经网络,来作为动作值函数的网络模型,并通过该网络模型Q(s,a;θ)模拟动作值函数Q*(s,a),即:

Q(s,a,θ)≈Q*(s,a)

(9)

在执行动作a后,当前状态s以概率P转移到s′,此时的Q函数为:

(10)

式中:r—状态s执行动作a后得到的奖励。

根据ε-贪心策略,笔者根据概率ε选取当前Q值最大的动作,根据概率1-ε随机选择动作后得到Q(s,a),故损失函数为:

L(θ)=(y-Q(s,a;θ))2

(11)

上式可以使Q函数依据ε-贪心策略在最小均方误差下收敛,得到最优Q值函数。

笔者根据式(10)来计算神经网络参数θ的梯度:

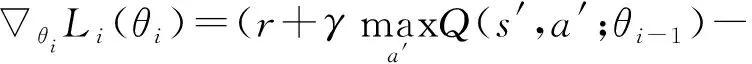
(12)

对于损失函数,笔者采用Adam算法进行训练。其中,动量β1为0.9,平方梯度动量β2为0.999,误差e为10-8。

1.4 ε-贪心策略

在强化学习任务中,对外界环境的探索是智能体获取知识的主要方式,所以在探索和利用之间平衡也就成了强化学习需要解决的问题。探索过多会使模型的收敛速度有所影响,太多的利用又会使强化学习模型进入局部最优。常用的ε-贪心策略多为固定值。本文使用一种随训练步数而变化的方法,使模型在前期多探索,后期多利用。

ε的设定方法为:

(13)

式中:i—当前的步数;T—总步数。

2 随机置零

为使模型有不错的抗噪性能,笔者使用随机置零的方法,即在信号输入后利用Dropout进行处理。在实际工况下,测试信号往往都会掺杂随机噪声,可认为是对测试纯净信号的随机干扰;在输入信号后引入随机置零,可以使原始信号更好地模拟真实环境中的随机噪声环境。

随机置零的具体实现方式如下:

p～Uniform(0.1,0.8)
R～Bernoulli(p)
Z=Y*R

(14)

式中:Y—原始振动信号;Z—随机置零后的振动信号;p—随机置零率,服从均匀分布U(0.1,0.8);R—服从概率为p的伯努利分布。

随机置零的使用可以看作是为原始信号添加随机干扰。当模型学习到这种经过被随机干扰过的样本后,模型的抗干扰性就会有所增强。

当然,随机置零方法也可以丰富训练样本的数量,即使是同一个样本信号,在经过随机置零后,输入模型的信号也很难保持一致。使用随机置零方法破坏了原始信号的局部特征,但可以迫使模型学习其他更为有效的细节特征或样本的整体特征[13]33-34。

随机置零与无监督学习方法中的去噪自编码器有相似之处,都向原始输入信号中加入随机干扰;其与去噪自编码器类似,都可以学习鲁棒性更强的特征。

3 深度Q网络故障诊断模型

此处笔者提出一种基于深度Q网络的智能故障诊断模型,并在抗噪性和提高准确率上进行了探索。

为了使模型得到不错的抗噪性能,笔者加入了随机置零的方法。

文献[13]31中指出,在原始数据输入后为其按一定比例随机置零,当数据被置零后,可以看作为数据引入了噪声;由于传统的深度神经网络多存在局部最小值和过拟合等问题,使得模型训练后存在准确率不高,且稳定性较差的问题。

笔者在深度神经网络中加入了Q学习策略,用来提高模型的识别准确率和稳定性。深度Q网络的故障诊断流程如图1所示。

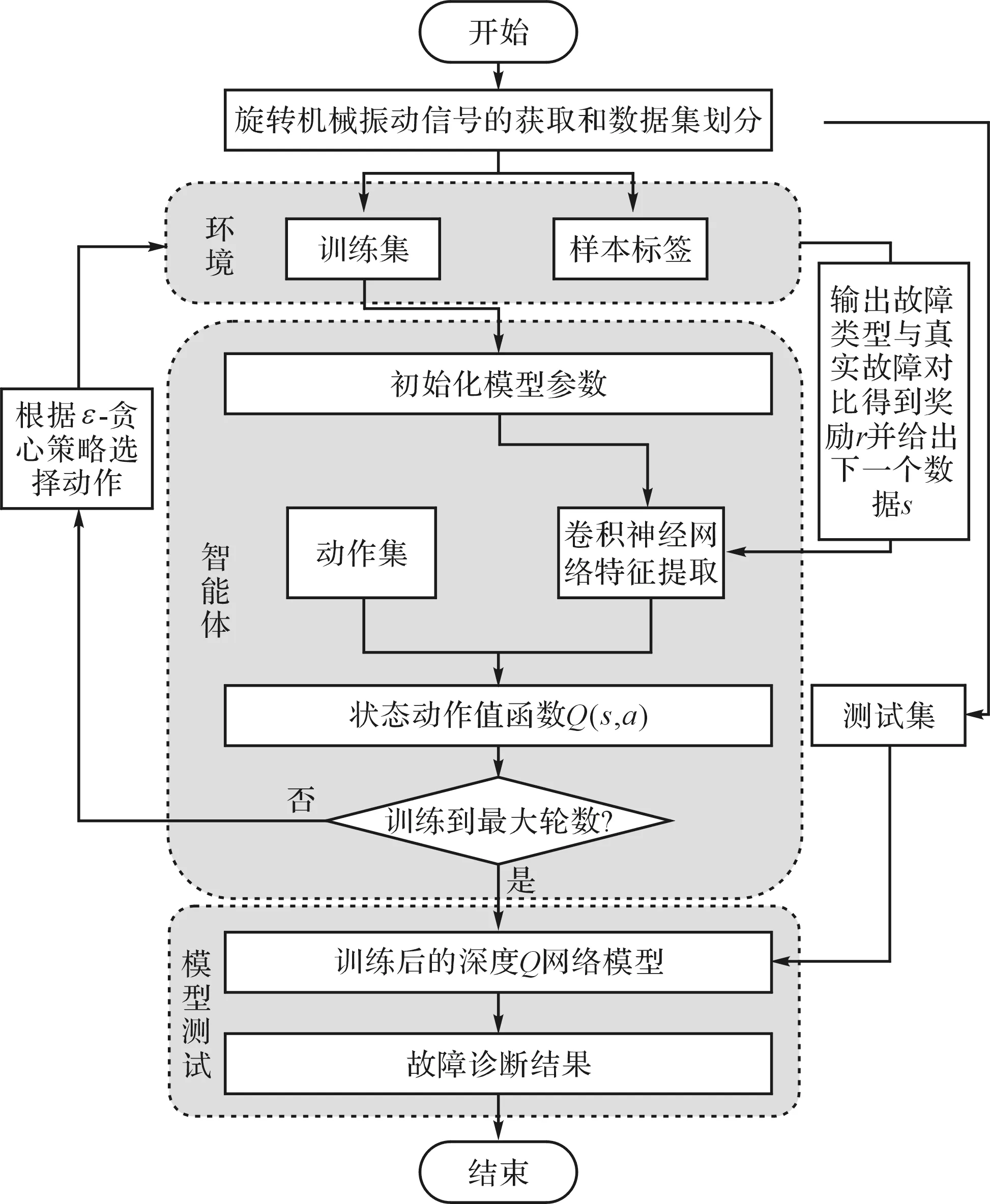
图1 深度Q网络故障诊断流程图

模型通过环境与智能体的交互来实现对故障的智能诊断。首先环境给智能体输入初始数据s,经过卷积神经网络拟合状态动作值函数Q(s,a)输出动作a,与环境中数据s的故障类型做对比,通过给予智能体奖励来更新卷积网络的参数,使模型达到预期效果。

模型的学习过程如下:

(1)初始化拟合Q值函数的权重参数θ;

(2)重复经验轨迹,从1到M:初始化状态(故障样本数据)s;

(3)重复对于当前输入状态(故)s,利用ε-贪心算法选择下一个动作a(某个故障类型);

(4)观察输出动作与环境中该故障数据对应的样本标签是否一致,一致则奖励r=+1,否则r=-1;

(6)对(y-Q(s,a;θ))2使用梯度下降类算法更新网络参数。

4 实验与结果验证

为了验证该模型的有效性,笔者使用SpectraQuest公司设计的实验台进行故障模拟实验。故障诊断试验台如图2所示。

图2 动力传动故障诊断试验台

实验所用齿轮箱为定轴齿轮箱,深沟球轴承的型号为ER-10K,节径D=33.5 mm,轴承的滚动体直径为7.9 mm,接触角α=0^°(该轴承有8个滚动体)。

定轴齿轮箱的结构图如图3所示。

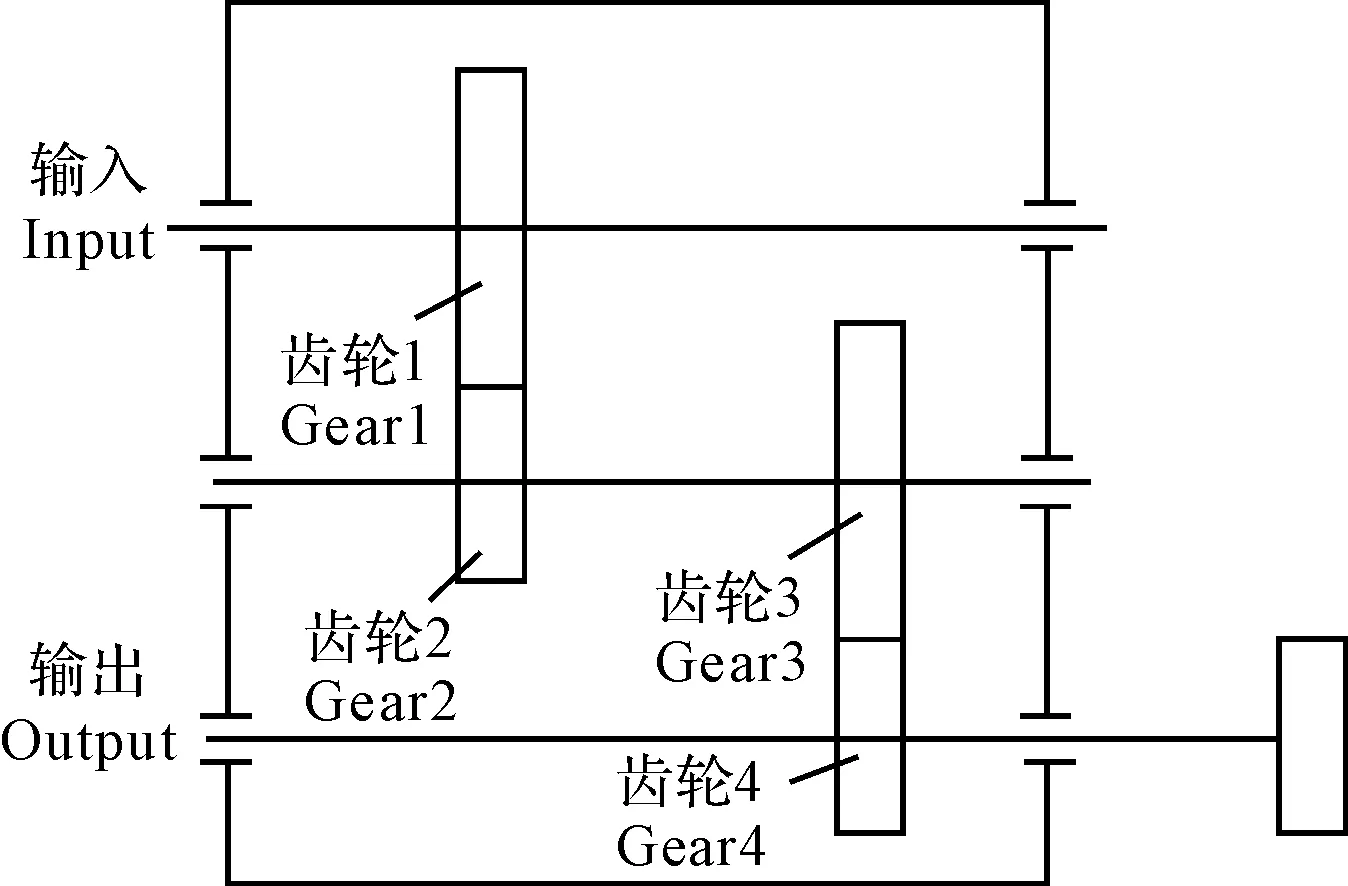
图3 定轴齿轮箱构造图

加速度传感器分别采集水平、垂直、轴向方向上的信号,通过数据采集仪(型号为DT9837)存储在计算机上。数据采集过程中,电机转速为1 200 r/min;轴承数据使用垂直径向采集的故障数据,信号的采样频率Fs为2 560 Hz;齿轮信号的采样频率Fs为5 120 Hz,采样时间均为10 s;

使用的信号故障类型为:外圈故障、内圈故障、正常轴承、滚动体故障、正常齿、磨损齿、缺齿、断齿、齿根裂纹[14]。

4.1 数据处理

模型的输入为一维时域信号。由于深度学习网络需要大批的数据作为训练样本,本文使用样本扩充的方式,其示意图如图4所示。

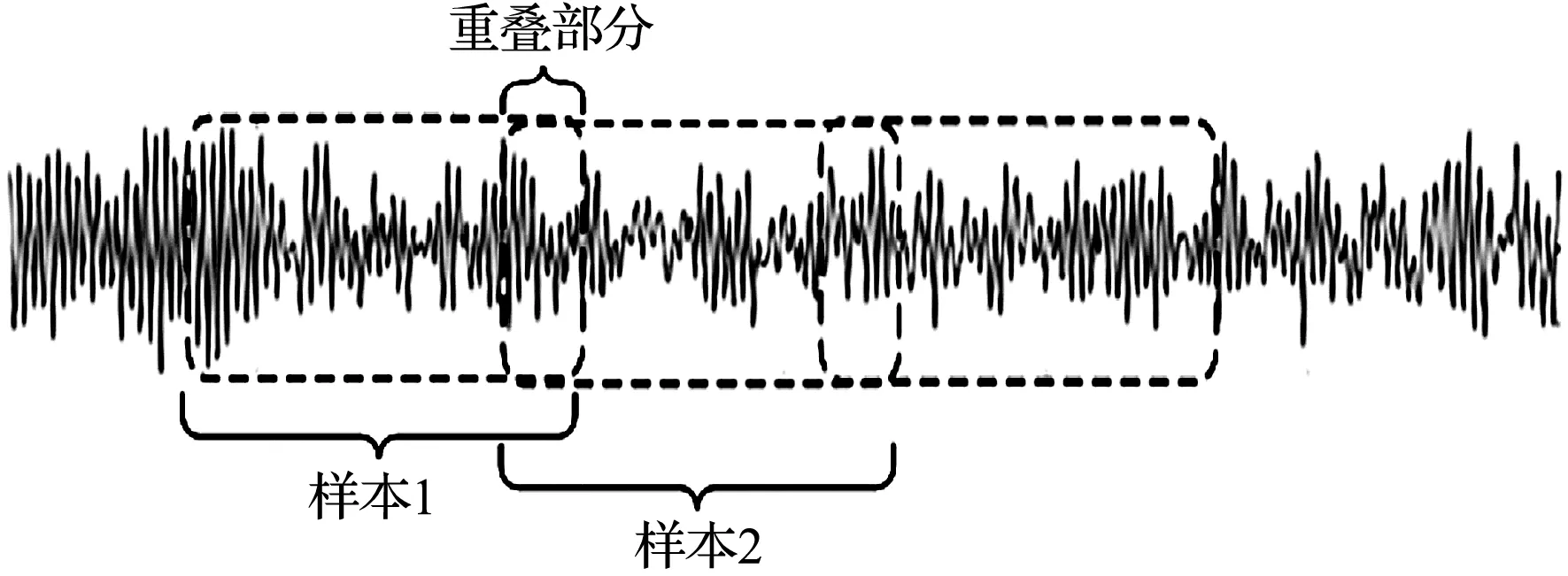
图4 样本扩充示意图

与没有样本重叠分割的方式相比,采用有重叠的样本分割策略,不但可以保留样本相邻数据之间的关联性,也可以满足深度学习方法对样本数量的要求[15]。

为保证在测试样本中有没有被训练的数据,此处取样本长度为1 200,重叠部分长度为300。

4.2 深度Q学习模型可行性验证

为了验证深度Q网络模型在故障识别方面的性能,本文使用上述试验台中采集的轴承数据进行验证实验。所使用的轴承数据包含:内圈故障、外圈故障、滚动体故障和正常轴承4类故障(均未添加负载)。

4种故障类型的时域图如图5所示。

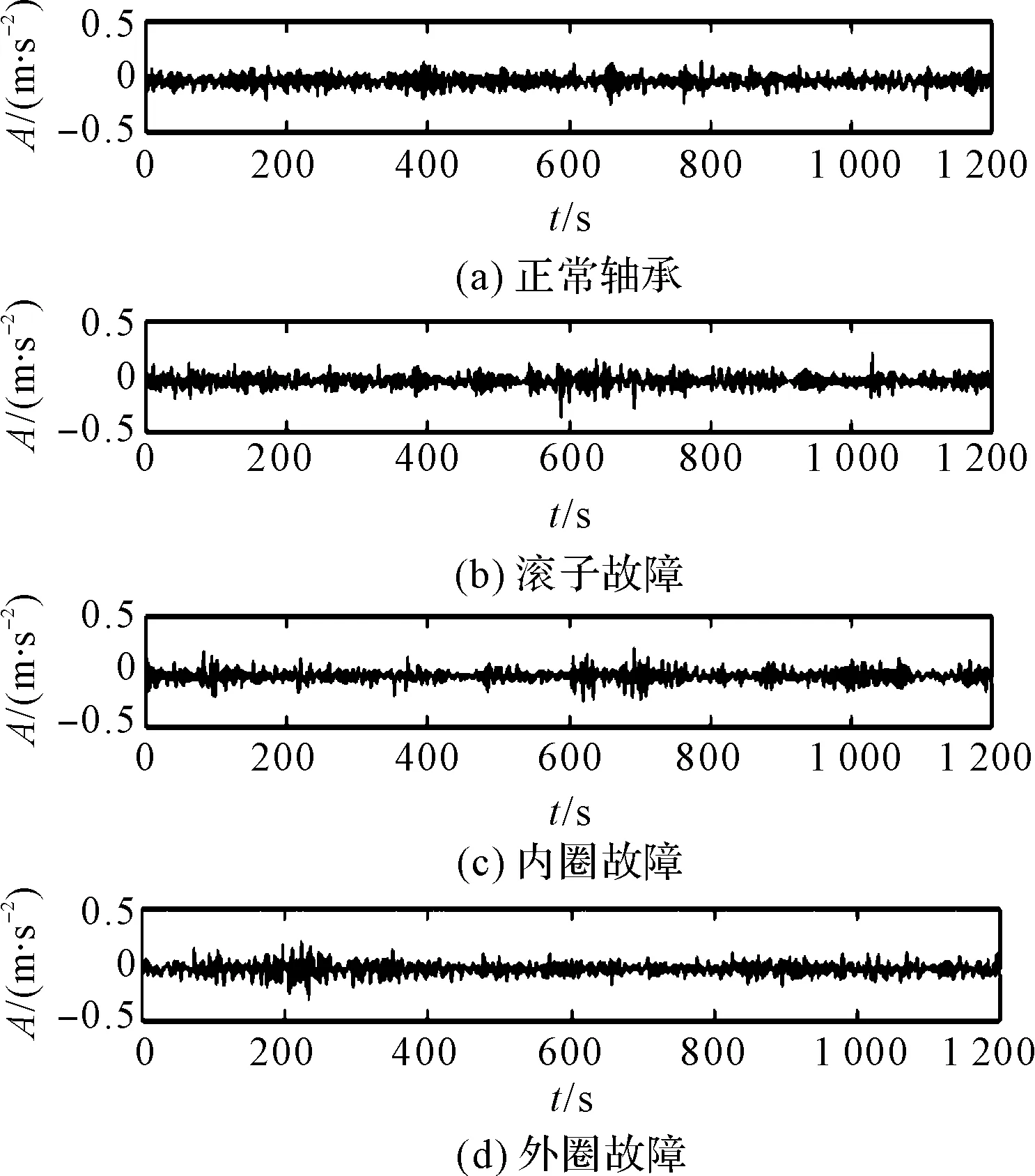
图5 故障时域图

此处,对应4种轴承状态,每种状态取1 000个样本,共4 000个样本,每个样本包含1 200个数据点。其中,90%是训练样本,10%是测试样本。

实验软件环境为:Python+Tensorflow2.0;硬件环境为:Intel i5-8250U。

模型使用的卷积神经网络拟合Q函数结构如图6所示。

图6 卷积神经网络拟合Q函数

本文使用卷积神经网络来拟合Q值函数[16]。第一层卷积层的卷积核大小为,步长为6,共32个特征图(较大的卷积核可以用于有效地提取大尺度下时域信号特征)。

本文将第二、三层卷积层用于提取信号的深层特征,卷积核大小均为5×1,步长为3,网络在该位置的输出由具有局部不变性的卷积层处理;通过对卷积的输出特征使用最大池化,使网络在保持信号本质的同时减少数据量(池化核的宽度均为3×1,步长为2)。

激活层使用的激活函数为Relu。全连接层可以把这些特征都连接起来,并且可以使网络增强学习特征的能力,其中分别包含128个和4个神经元。

在原始数据输入后加入随机置零,即加入一层Dorpout层,置零比例在0.1～0.8之间均匀分布。

模型的训练参数如下:

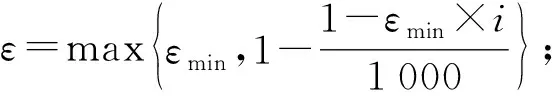
在每轮训练中,该模型每轮设置的步数为512步。由于模型开始时没有学习任何内容,一开始有1/4的概率可以被猜中,也就是首轮的得分应该在-512～-456分之间,模型共训练2 000轮。本文对2 000轮训练的每10轮计算奖励和损失值的平均值。

模型训练后的Q函数累计值随迭代次数的关系,即Q函数累计值变化图,如图7所示。

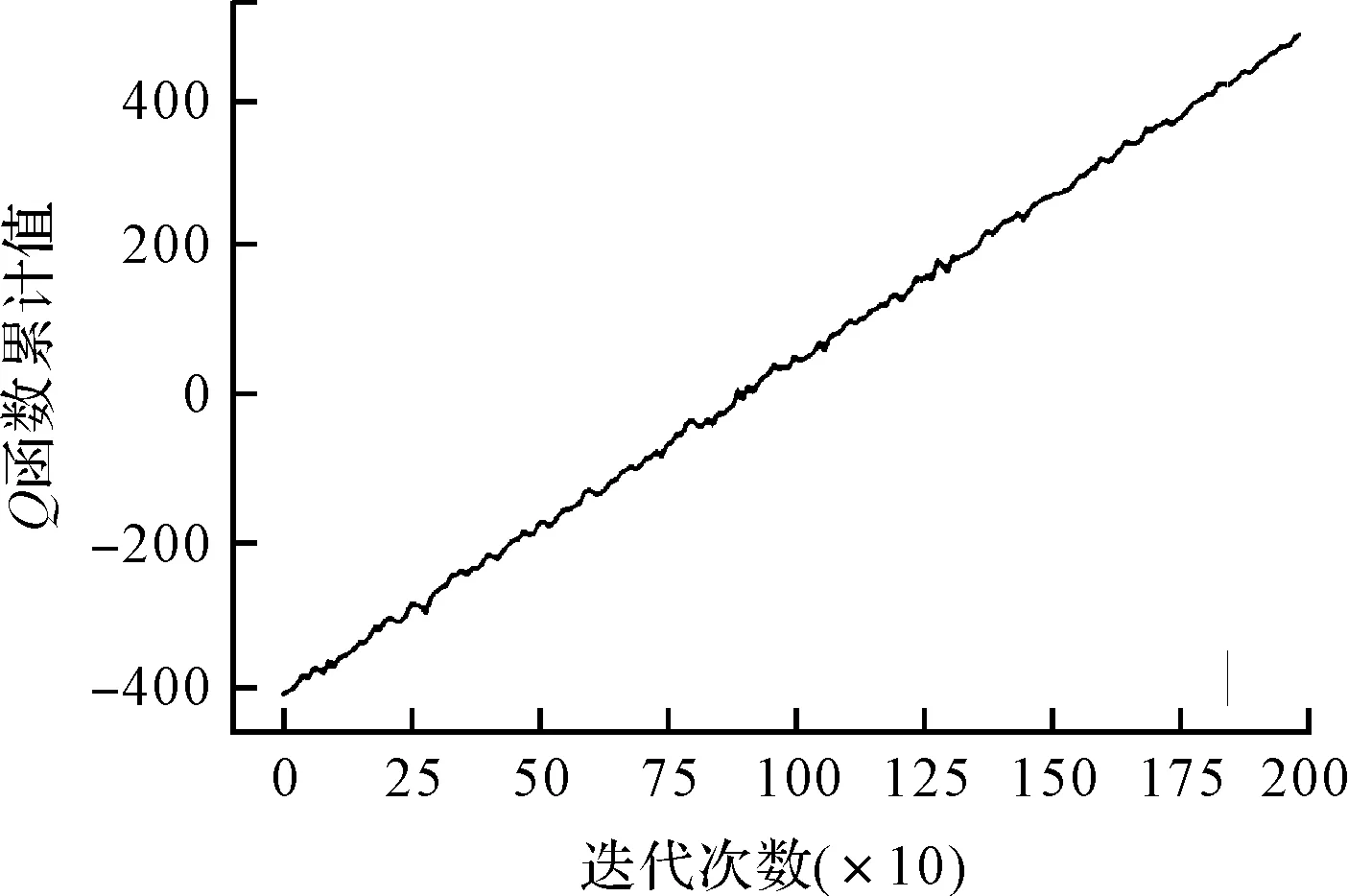
图7 Q函数累计值变化图

由图7可知:模型几乎是线性递增的,最后最高得分达到了488分;模型的识别准确率可以达到98.87%。

损失值变化图如图8所示。

图8 损失值变化图

从图8可以看到:每轮训练后模型的损失值都可以保持在比较低的状态,表明模型每轮训练都学习到了东西;在迭代到150次时,损失值会有明显降幅,模型开始收敛,在训练过程中由于模型不定时“探索”会出现损失值的跳动。

上述实验结果验证了该方法在故障诊断中的可行性。

4.3 探索与利用的平衡

在强化学习任务中,探索与利用的平衡通常由ε-贪心策略来实现。过大或是过小的ε都会极大地影响探索和利用的平衡。研究人员在训练前期可以进行探索,后期可以利用已学到的内容,所以本文在此处使用动态值。

为验证动态值的优势,笔者使用固定ε值进行了比较,其实验结果如表1所示。

表1 ε值对Q函数累计值的影响

由表1可知:当ε=0.75时,模型探索过多,不能被有效利用,Q函数累计值较低;当ε=0.3时,模型不能很好地进行探索,但在充分迭代后,Q函数累计值也可以达到458;使用动态ε值时,可随迭代步数变化,使前期探索后期利用,可以看到Q函数累计值达到了488。

4.4 抗噪能力验证

为研究模型在不同噪声环境下对旋转机械故障的识别能力,笔者在上述模型分中别输入不同信噪比(σSNR)的测试样本。信噪比公式为:

(15)

式中:Psignal,Pnoise—信号的有效功率和噪声的功率。

在采集到的不同故障的测试集中,笔者分别添加了不同信噪比的高斯白噪声。

正常齿轮信号中再加入0 dB噪声后的时域图,如图9所示。

图9 正常齿轮信号加入0 dB噪声

此处仍然利用SpectraQuest公司的试验台数据作为实验数据。样本的具体划分如表2所示。

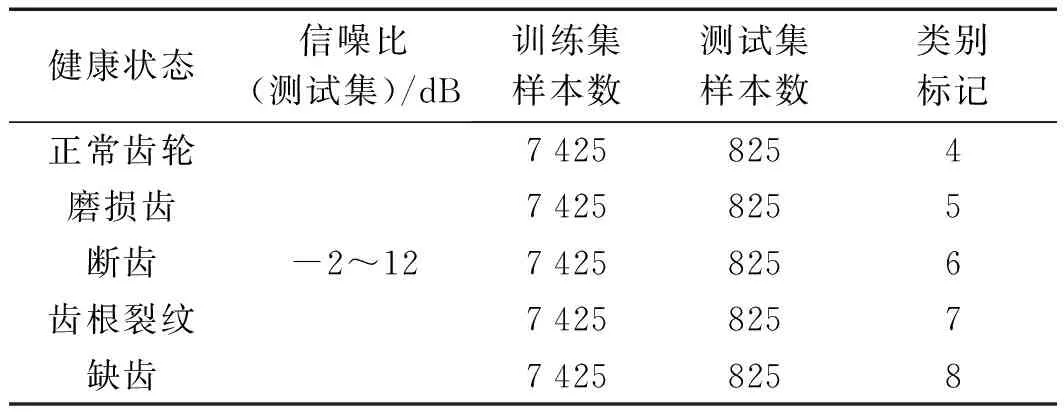
表2 数据集划分

样本共41 250个,其中,训练样本37 125个,测试样本4 125个。测试样本中都包含着数量相同的加噪信号。

本文通过向原始信号随机置零加入Dropout层,以增加模型对噪声的泛化性。

有随机置零策略、没有随机置零策略以及置零比例在0.1,0.3,0.5,0.6时,抗噪性能的对比结果如图10所示。

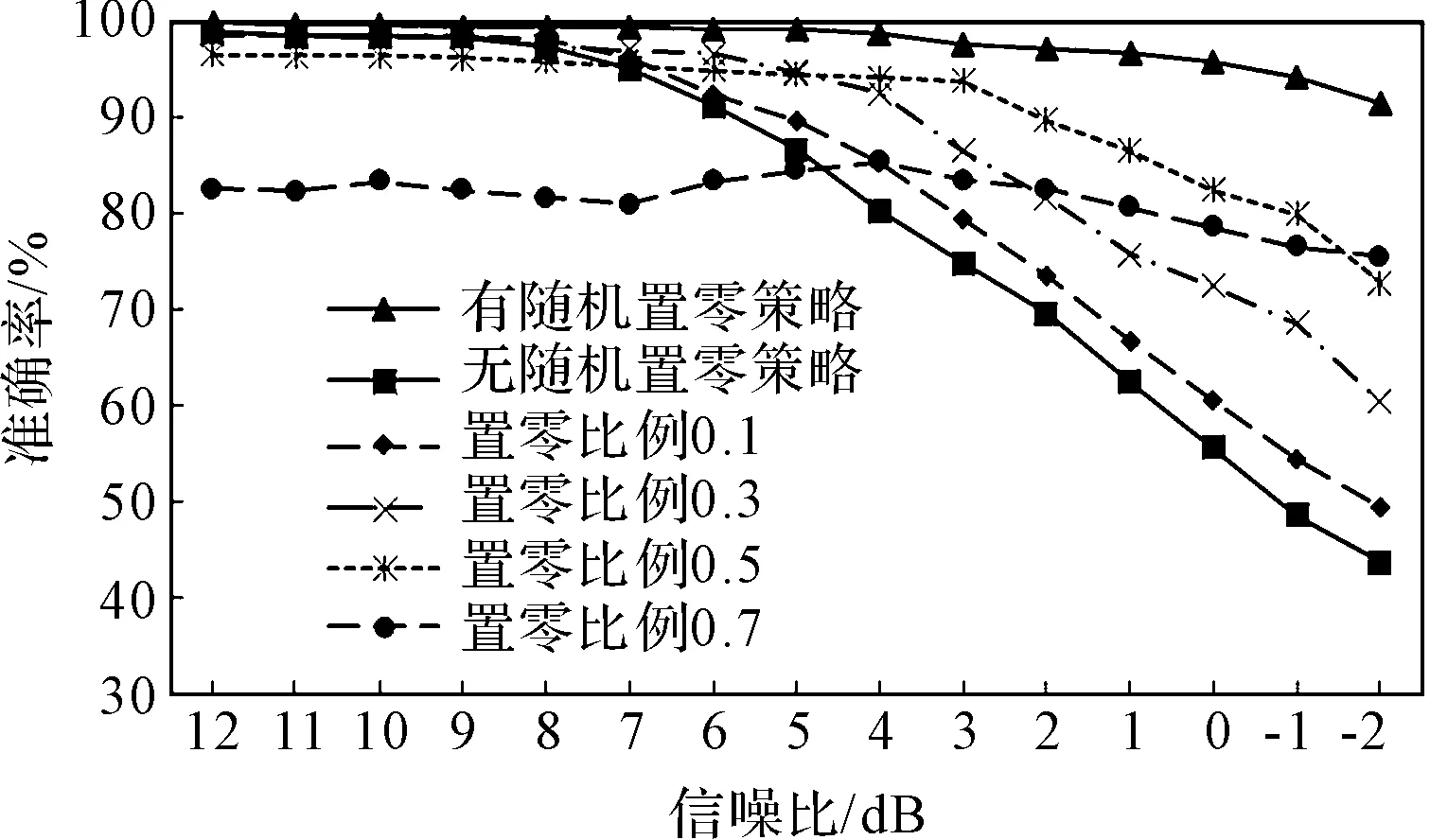
图10 有无随机置零输入信号的诊断性能

从图10中可以看出:模型在没有随机置零输入信号的情况下,故障诊断的识别精度会随信噪比的降低而迅速下降;而在有随机置零输入信号的情况下,模型则表现出了良好的抗噪性。

4.5 美国凯斯西储大学数据验证

由于上述轴承和齿轮的故障数据都是在固定负载下获取的,此处本文使用美国的凯斯西储大学的轴承数据集来验证变载条件下的准确性[17]。

此处利用的数据是驱动端数据,数据中包含轴承正常、滚子故障、内圈故障、外圈故障4种故障状态,每种故障类型各包含(1 hp、2 hp、3 hp、4 hp)4种负载的数据,它们所对应的转速分别是1 797 r/min、1 772 r/min、1 750 r/min和1 730 r/min,大致可以认为是定速;振动数据的采样频率为12 kHz。

对于上述的4种故障类型,每种故障类型都有8 100个样本数据。西储的数据集划分如表3所示。

表3 西储数据集划分

笔者使用经过随机置零处理的数据和没有随机置零的数据训练模型进行测试和对比,其结果如表4所示。

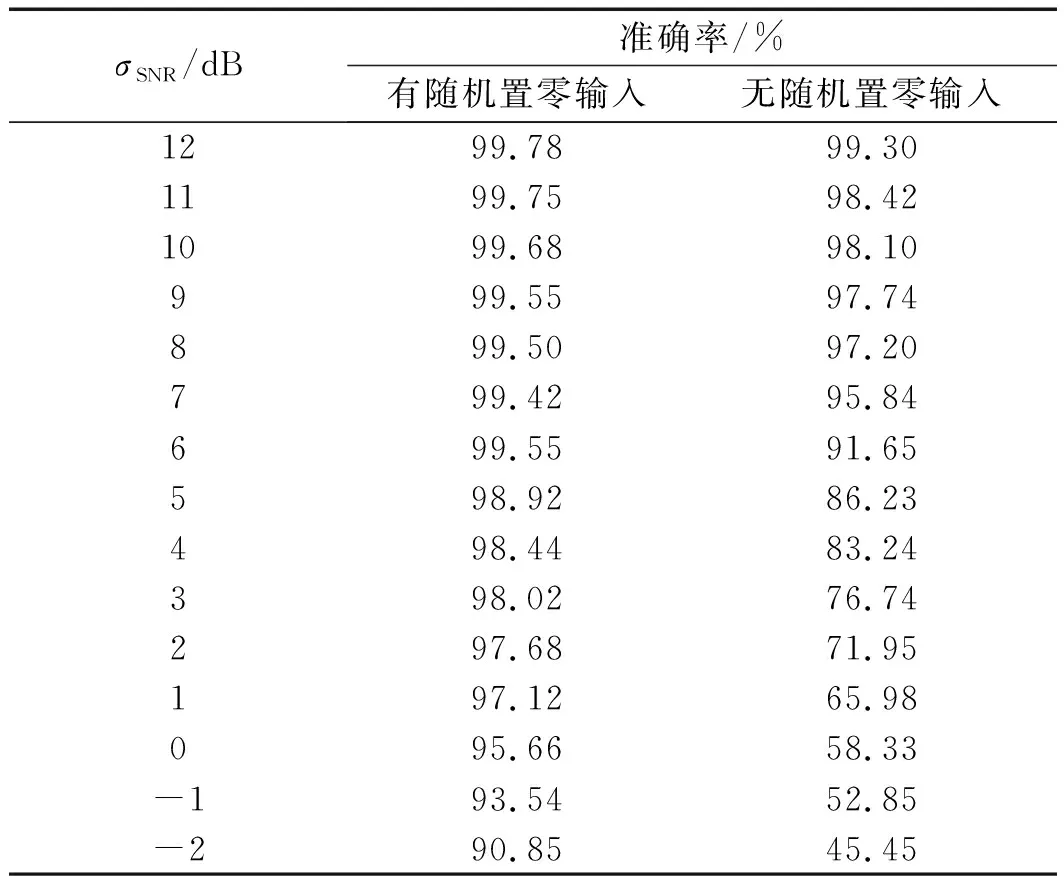
表4 有无随机置零输入时模型的准确率

由表4可知:在测试集上的故障识别准确率方面,经随机置零处理的数据训练的模型均远高于干净信号输入训练的模型,并且模型在信噪比为-2 dB时仍有着90.85%的诊断精度,而采用干净信号输入的模型仅有43.52%的识别准确率;模型在信噪比>2 dB时识别准确率可以达到98%,信噪比>5 dB时模型的识别准确率更是有99%。

由此可见,在变载的条件下,该模型有着较好的识别准确率。

4.6 模型对比实验

本文对一维卷积神经网络(1DCNN)、支持向量机(SVM)、BP神经网络(BP-NN)和本文模型进行对比实验。其中,三层卷积池化层、两层全连接层和Softmax分类层构成了1DCNN,支持向量机采用高斯核函数,BP-NN采用三层网络结构。

模型的训练结果如图11所示。

图11 不同噪声环境下方法诊断性能对比

由图11可知:与1DCNN相比,本文模型在高信噪比时都有着不错的故障识别精度,而当信噪比<2 B时,1DCNN的诊断精度略低于本文的方法,在信噪比为-4 dB时该模型的识别准确率也有78%;

在稳定性方面,1DCNN在噪声比较严重的情况下有2.15%的识别误差,而本文方法则表现相对稳定,误差在0.86%。

与相对典型的SVM、BP-NN相比,本文模型在识别准确率、稳定性上均有不错的优势;而SVM、BP-NN即使在噪声较小的数据集上诊断效果也不佳,其原因主要在于浅层模型无法有效学习特征,同时学习到的特征也没有具备较好的分类特征。

5 结束语

由于传统的旋转机械故障诊断方法需要人工提取故障特征,且受环境噪声的影响较大,笔者提出了一种基于深度Q网络强化学习的故障诊断模型,探索了一种端到端的,基于深度强化学习的旋转机械故障诊断的方法,并使其能够准确且稳定地在噪声环境下和变载条件下对旋转机械进行故障诊断。

该研究过程和结果如下:

(1)该方法使用原始信号作为输入,可有效省去现有方法需要通过人工进行信号处理和特征提取的繁琐过程;

(2)采用随机置零的方法,使模型对不同程度噪声均产生抗噪性,经过训练的模型可以大大地提升其抗噪水平;

(3)通过不同模型的对比实验表明,与1DCNN、BP-NN和SVM相比,在准确度和稳定性方面,本文提出的模型都有着不错的表现。在信噪比>-2 dB时,模型识别准确率可达90%左右;在信噪比>-4 dB时,准确率也可达78%。

在后续的研究中,笔者将探索不同奖励函数对网络的影响,并将其结果与迁移学习相结合,以拓宽该模型在不同设备间的适用性。