基于二阶瞬态提取变换的滚动轴承故障特征提取方法研究*

彭程程

(珈蓝电力科技有限公司,浙江 杭州 311200)

0 引 言

远程带式输送机是一种成本低、效率高、距离远的连续型运输装备,在工业生产领域尤其是能源、钢铁以及煤矿等行业得到了广泛应用。

托辊滚动轴承故障是带式输送机最常见的故障之一,对托辊滚动轴承进行有效的状态监测和故障诊断具有重要的意义[1-4]。

实际工况中,托辊故障轴承振动特性以冲击性特征为主,冲击时刻和冲击幅值具有明显的时变性,这种时变性主要表现在以下两个方面[5-7]:(1)与滚动体、内外圈等部件表面不规则性和滑移效应有关的不可再生现象导致的随机性,即使稳速工况下的轴承其故障点和配合部件之间碰撞产生的冲击成分也不具备严格的周期性,而是呈现一定程度的随机性;(2)托辊在带式输送机中具有支撑作用和承载作用,并在皮带和标准套筒摩擦力的驱动下工作,负载的大小和分布的时变性导致托辊滚动轴承处于变负载、变转速的非平稳工况。

鉴于以上分析,传统的以平稳转速和弱背景噪声为前提的共振解调方法将不再适用于对托辊滚动轴承进行故障诊断[8,9]。

针对变负载、变转速工况下滚动轴承故障特征提取问题,时频分析是一种有效的方法[10-12]。然而由于海森伯格不确定原则,以及时变冲击造成的频率模糊问题,由于时频聚集性差,传统的时频分析往往不能提取到有效的故障特征。对此,诸多学者开展了深入研究,并提出了一些相关的解决方案。

赵德尊等人[13]提出了基于自适应广义解调变换的滚动轴承时变非平稳特征提取方法,该方法从高频共振成分的包络时频谱中提取时频脊线,并构建广义特征指标模型,在无需转速信号的情况下,实现了对非平稳故障特征的有效提取。王宏超等人[14]在改进基于二阶循环统计量的谱相关分析方法的基础上,提出了一种新的具有强抗噪能力的时频分析方法,并利用该方法提取到了更为有效的故障特征。刘东东等人[15]提出了基于故障特征趋势线模板的滚动轴承故障诊断方法,该方法利用线调频小波路径追踪算法,提取瞬时故障特征频率趋势线,然后根据故障特征趋势线搜索轴承故障特征。高冠琪等人[16]提出了一种基于时频挤压的转频估计方法,结合阶比分析,实现了对变转速工况下轴承故障特征的提取。

上述时频分析方法在一定程度上提高了非平稳工况下轴承故障特征提取的精度,然而这些方法都建立在振动信号的瞬时频率在时间轴上具有局部平稳性的前提基础上,与滚动轴承故障信号时变冲击成分短时、快速衰减以及频带宽的特点不匹配。

针对托辊滚动轴承的瞬时非平稳时频特征,YU G等人[17]在同步挤压变换[19]、时间重排同步挤压变换[19]以及瞬态提取变换[20]等高精度二次时频分析技术的基础上,提出了二阶瞬态提取变换方法,该方法能够在复杂噪声干扰的情况下,实现具有良好时频聚集性的时频分析。

本文将上述二阶瞬态提取变换算法应用于远程输送机托辊滚动轴承故障诊断中,在构建的二阶频率变化模型和时频重排算法的基础上,实现高精度的时频分析,准确提取故障信号时变冲击成分的瞬时频率和瞬时幅值等时频特征,进而判断故障类型;在仿真信号和工程实际信号中,分别运用该方法和短时傅里叶变换提取时频特征进行对比,以验证该方法在变负载工况下提取故障特征的准确性和工程实用价值。

1 滚动轴承故障信号建模

当滚动轴承发生故障时,故障点和配合部件之间发生碰撞会产生一个短时、高幅值且快速衰减的冲击,该冲击会随着轴承的运转而形成冲击序列,同时引起系统产生高频共振。

冲击重复的频率就是故障特征频率,即:

fimp=frφ(d,D,nRE,α)

(1)

式中:fr—转轴频率;φ—与故障类型以及轴承几何尺寸有关的常量系数;d—滚动体直径;D—轴承节径;nRE—滚动体个数;α—接触角。

通常的故障特征频率包括:内圈故障频率(ball pass frequency inner race, BPFI)、外圈故障频率(ball pass frequency outer race, BPFO)、滚动体故障频率(ball spin frequency, BSF)以及保持架故障频率(fundamental train frequency, FTF)4种类型。

早期的滚动轴承故障信号往往呈现出一定的周期时变性和循环平稳特性。通常认为,伪二阶循环平稳模型能够比较好地匹配故障信号的复杂特征。

离散故障振动信号可表示为:

(2)

式中:t—离散时间序列;θ—离散角度变量;i—冲击序号;δ—时间延迟狄拉克δ函数;h—冲击响应函数;T—随机变量;Q—表征幅值调制的非负周期函数;N—服从高斯分布的表征幅值随机性的变量。

对变负载、变转速非平稳工况下的滚动轴承故障信号进行建模时,不仅要考虑时间因素的影响,同时,角度因素对模型的准确性也有很大影响。

随着故障点的扩展和故障程度的加深,晚期滚动轴承故障振动信号中的冲击性成分衰减速度有所减弱,冲击持续的时间相对变长,此时的轴承故障信号可用二阶循环平稳模型表示,即:

(3)

式中:PREB—信号中的周期性成分;QREBN[0,1]—经过QREB幅值调制的零均值、单位方差的高斯白噪声,对应故障信号中循环频率为QREB阶数一半的二阶循环平稳成分。

式(2,3)说明:在滚动轴承生命周期的不同阶段,故障信号中的冲击性成分具有不同的特征,该特征可以用来作为判断故障程度和故障类型的一个指标。

2 基于STET的滚动轴承故障特征提取

2.1 二阶瞬态提取变换(STET)

二阶瞬态提取变换,即是在短时傅里叶变换(STFT)的基础上,根据滚动轴承故障信号冲击性成分的时频特征,压缩、重排时频曲线,以达到提高时频聚集性和分辨率的目的。

其信号的STFT变换为:

(4)

式中:g(u-t)—滑动窗。

故障信号中的冲击性成分通常用狄拉克δ函数表示为:

s(t)=Aδ(t-t0)

(5)

式中:A—冲击成分幅值;t0—冲击发生的时刻。

把式(5)代入式(4),可得:

G(t,w)=Ag(t0-t)e-iwt0

(6)

理想情况下,狄拉克δ函数的STFT变换结果应该集中在冲击发生时刻t0,时频分析算法通常使用二维群延迟重排发散的时频能量,为:

(7)

根据式(6,7)得到:

(8)

式(8)说明冲击成分STFT结果的二维群延迟聚焦于发生时刻t0。

根据这种特性,二阶瞬态提取变换首先构建二阶频率变化模型,即:

(9)

借助于窗函数g(t)=e-(2σ)-1t2,式(9)的STFT变换为:

(10)

式(10)的二维群延迟为:

(11)

根据式(11)可得到:

(12)

式(12)提供了一种新的计算二维群延迟的路径,可以定义为:

(13)

(14)

利用式(14)可以得到式(9)的二阶瞬态变换为:

Te[2](t,w)=A(w)eiφ(w)δ(t+φ′(w))

(15)

2.2 故障诊断流程

基于上述分析,笔者给出了基于二阶瞬态提取变换的滚动轴承故障特征提取方法流程图,如图1所示。

图1 故障诊断流程

其具体步骤如下:

(1)获取振动信号,利用STFT得到二维时频特征表示;

(2)根据非平稳工况下故障信号中的时变冲击成分特征,构建二阶频率变化模型;

(3)在第(1)步STFT时频图的基础上,利用二维群延迟算法得到时频聚集性良好、能量集中的高精度时频特征表示;

(4)在估计共振频带的基础上,从步骤(3)高精度时频特征中提取时变瞬态分量;

提起蒋海峰，紫云还真有些不舒服：“老伯，你再这样说，我就生气了。衣服我收下，今后就不要为我乱花钱了。”

(5)计算时变瞬态分量的重复频率,结合轴承不同故障的特征频率,判断故障类型。

3 仿真分析

在变负载工况下,为了验证所提出的算法提取滚动轴承故障特征的有效性,笔者首先构造仿真信号对其进行验证。

根据式(2)中确定的表征滚动轴承早期故障的二阶循环平稳模型构建仿真信号,仿真信号模型参数如表1所示。

表1 仿真信号模型参数

ζ—阻尼系数;fn—系统共振频率;参数fc1,fc2,fm,fd—转频起始频率、终止频率、频率波动范围以及波动频率

确定转频曲线的公式为:

(16)

带式输送机托辊滚动轴承是在运输带的摩擦力驱动下工作,输送量的大小以及位置都是时变量,因此,笔者考虑用转速周期波动模型进行近似仿真;其中,fc1,fc2对应线性变化部分,fd和fm对应周期变化部分。

根据表1相关参数以及式(16),确定的转频曲线如图2所示。

图2 转频曲线

仿真信号波形如图3所示。

图3 仿真信号波形

从图3中可以看出:仿真信号以时变冲击为主要成分,冲击发生时刻和冲击幅值都具有一定的随机波动性,这和滚动轴承的故障特征比较符合。

STFT的变换结果如图4所示。

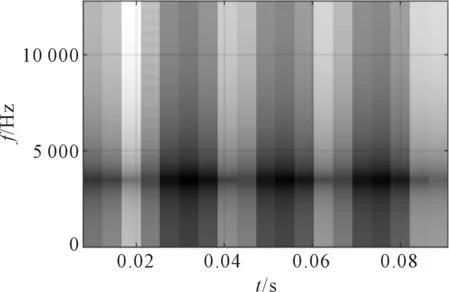
图4 仿真信号STFT

从图4仿真信号的STFT变换结果中,可以看到时变冲击成分的时频特征以及3 500 Hz附近的共振频带,但是由于冲击成分造成的频谱模糊以及能量发散,STFT结果时频聚集性较差,冲击序列时频特征之间存在交叉干扰,难以准确地判断故障信号的时频特征。

仿真信号二阶瞬态提取变换的结果及其局部放大如图5所示。

图5 二阶瞬态提取变换结果

由图5可以发现:(1)相对于STFT变换结果,二阶瞬态提取变换结果的时频能量聚集性大幅提升,可以清晰地展现冲击发生的时刻;(2)由于构建的二阶频率变化模型和信号特征更匹配,每个冲击成分的瞬时频率和瞬时幅值提取也更加精确,冲击成分在共振频率3 500 Hz处产生拐点,并具有最大幅值。

该结果和实际轴承发生故障时产生的高频共振特征相符合。

二阶瞬态提取变换在3 500 Hz附近的切片如图6所示。

图6 时变冲击发生时刻

由图6可知,共振频率切片可以准确对应冲击成分发生的时刻。

4 工程验证

为进一步验证所提算法的有效性,笔者在某电厂远程带式输送机上获取了实际工况下的托辊滚动轴承故障振动信号。

托辊滚动轴承型号为6305,带式输送机托辊如图7所示。

图7 带式输送机托辊

图7中,带式输送机托辊的工作转速为360 r/min左右,其滚动体个数、滚动体直径、节径以及接触角等尺寸参数如表1所示。

计算得到轴承故障特征频率如表2所示。

表2 托辊滚动轴承特征频率

在现场采集实验中,笔者设置采样频率25 600 Hz,采样长度25 600,采集得到的托辊滚动轴承振动信号波形如图8所示。

图8 托辊轴承振动波形

托辊轴承振动频谱如图9所示。

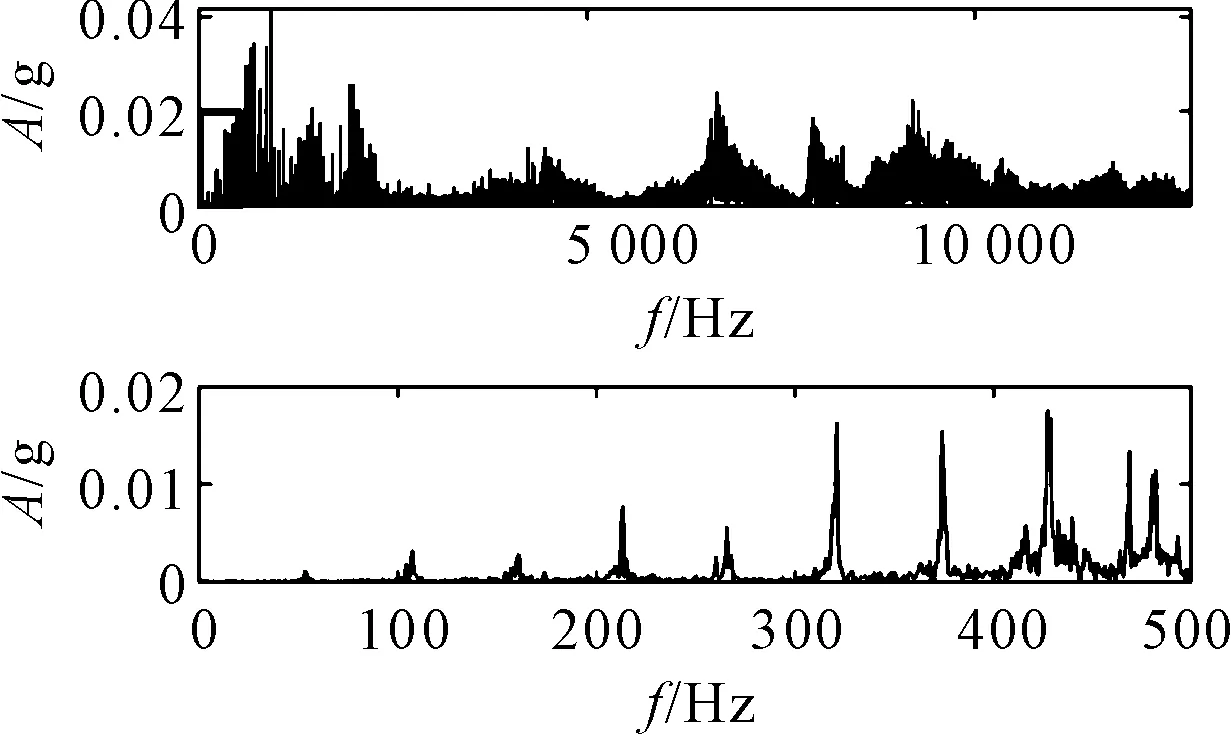
图9 托辊轴承振动频谱

为了清晰展现信号特征,笔者截取0.1 s时长的故障信号作为分析数据,其信号波形如图10所示。

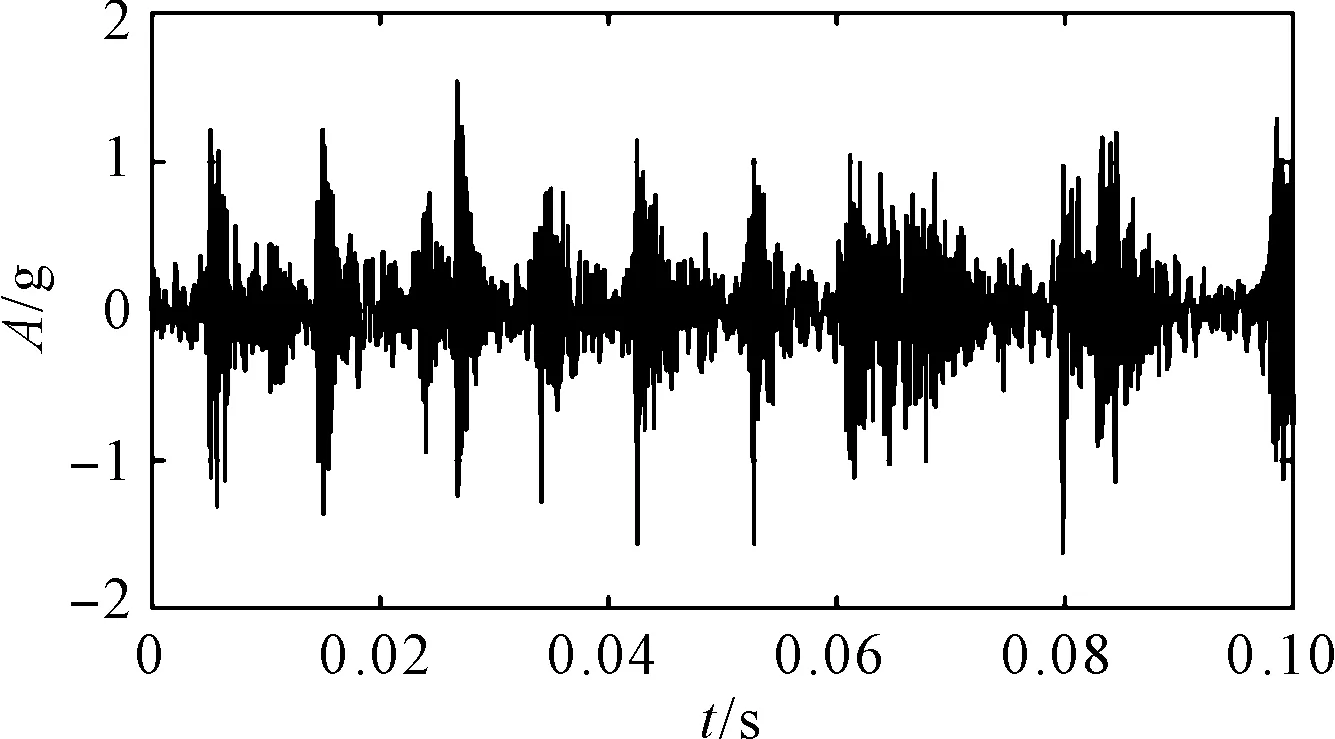
图10 托辊轴承振动波形

由图10可以看到:由于现场复杂的工况和其他振动干扰,托辊轴承故障信号成分复杂,时变冲击成分隐藏在噪声和干扰信号中。

故障信号的STFT变换结果如图11所示。

图11 托辊轴承故障信号STFT变换结果

从STFT时频特征中可以看到多阶倍频成分,但是由于能量发散和聚集性差,从中难以看到信号中时变冲击成分的时频特征。

二阶瞬态提取变换结果及其局部放大图如图12所示。

图12 托辊轴承故障信号二阶瞬态提取变换结果

从图12的二阶瞬态提取变换结果中可以看到:(1)由于现场实际故障信号成分复杂,单一冲击持续时间内,信号中冲击成分的时频分布不再是一条宽频曲线,而是多条频率曲线构成,但是对冲击序列中的不同冲击仍然有比较好的区分能力;(2)二维时频图中瞬时幅值的分布特征和仿真信号类似,在轴承自身共振频带、系统共振频带等多个共振频带内都有明显的峰值。

基于STFT的冲击时刻提取如图13所示。

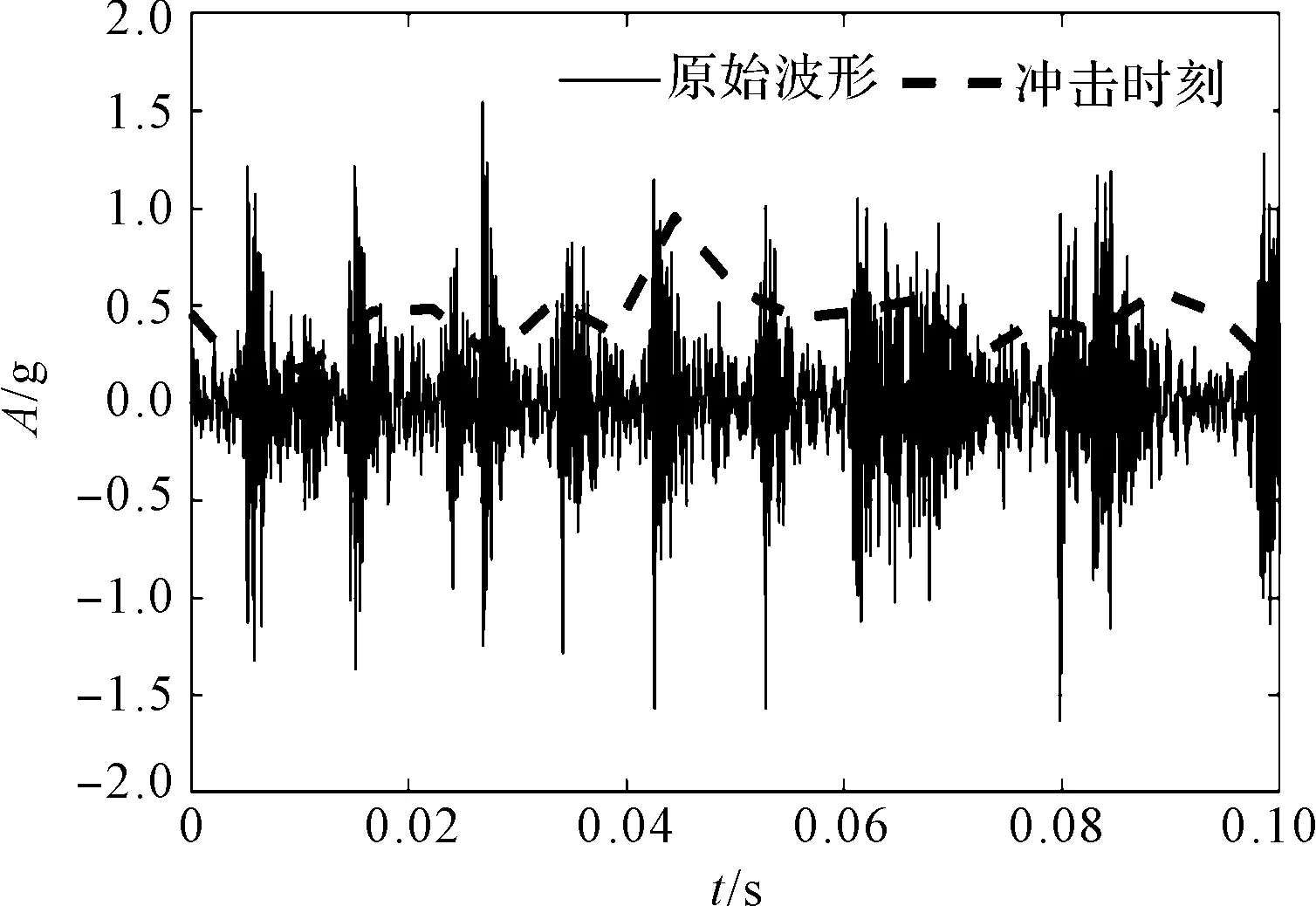
图13 基于STFT的冲击时刻提取

从图13中可以看到,基于STFT的冲击时刻提取结果存在明显的偏差。

基于二阶瞬态提取变换的故障信号冲击成分发生时刻提取结果,如图14所示。

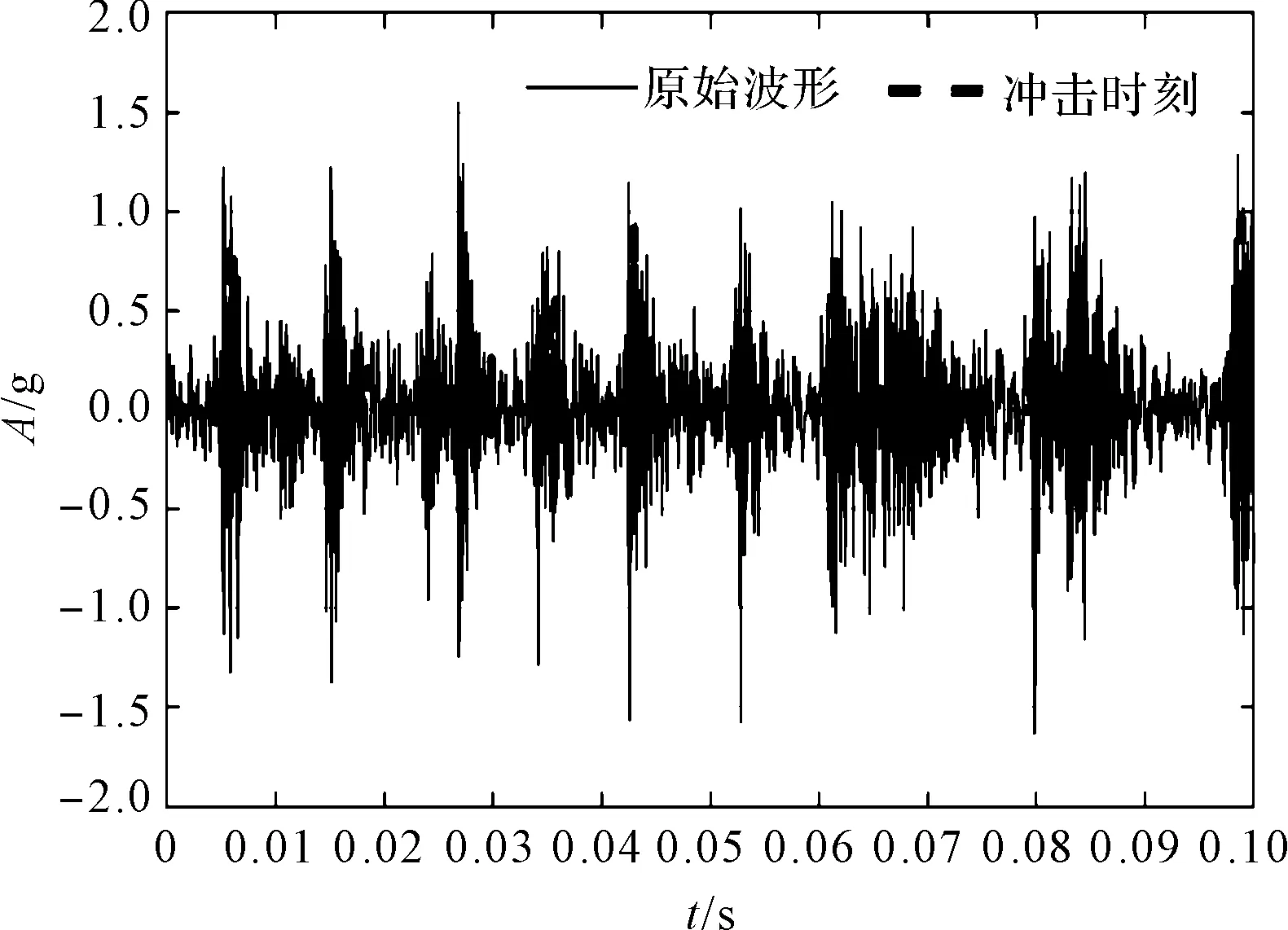
图14 基于二阶瞬态提取变换的冲击时刻提取

在图14中,较为清晰地展现出了冲击发生的时刻;其中,主要冲击成分重复的频率为106.9 Hz和53.32 Hz,分别是托辊滚动轴承内圈故障特征频率26.52 Hz的4倍频和2倍频,由此可以判别该轴承发生了内圈故障。

5 结束语

采用传统的时频分析方法难以提取变负载工况下的远程带式输送机托辊滚动轴承故障特征,针对这样一个问题,本文通过构建能够匹配时变冲击成分频率变化规律的二阶频率变化模型,利用二阶瞬态提取变换,实现了对故障信号高精度的时频特征表示;并利用仿真数据和工程实际数据,对该方法的有效性进行了验证。

研究结果表明:

(1)与时间变化模型相比,本文构建的二阶频率变化模型更符合带式输送机托辊滚动轴承的故障特征,且二阶瞬态提取变换提取得到的时频特征更加准确;

(2)二阶瞬态提取变换结果的时频能量聚集性大幅提升,冲击成分在共振频率处的重复频率对应轴承故障特征频率,可以用作判别轴承故障类型的有效依据。

以上研究结果表明,二阶瞬态提取变换能够提取表征带式输送机托辊轴承故障特征的时频信息。

在下一步的研究工作中,笔者将结合机器学习与人工智能算法,以实现对输送机状态的实时动态监测与故障的智能诊断。