天津市地下水位数据过滤方案分析比较

吴 逊，郭建琴

（天津市水文水资源管理中心，天津 300061）

目前采用的地下水信息接收处理系统在处理地下水位数据时会产生大量误报和漏报。笔者通过讨论天津市地下水动态变化影响因素，对其方案（以下简称原方案）存在的问题进行分析，并以站点特性为基础建立数据过滤方案（以下简称新方案）。最后，选取多个典型站点数据系列，对比2 个方案在数据误报、漏报等方面的差异，并分析其产生原因。

1 地下水位动态变化影响因素

天津市地下水位动态变化主要受气象、水文、地形地质、生态和人类活动等因素综合影响[1]。其中，浅层地下水与降雨蒸发关系密切，一般通过降雨入渗、渠系渗漏、田间灌溉等方式补给；地下水主要通过潜水蒸发、越流排泄和人工开采等方式排泄。深层地下水与人工开采关系密切，主要补给量包括侧向补给量、越流补给量，排泄量主要是人工开采量。

2 原方案数据过滤方式的分析

2.1 原方案数据过滤策略

原方案以前一个正常水位Z0和变幅阈值ΔZ为依据，检查当前水位Z1是否正确。如果Z1在水位上限（Z0+ΔZ）与下限（Z0—ΔZ）之间，那么认为Z1是正常水位，与ΔZ一同作为新的依据检查下一数据；否则，认为Z1是异常水位，将其过滤。

2.2 存在问题及原因分析

假设某站点的正常水位是10 m，在动态过程中存在异常。采用原方案对数据进行过滤，变幅阈值ΔZ设为3 m，过滤结果如图1所示。

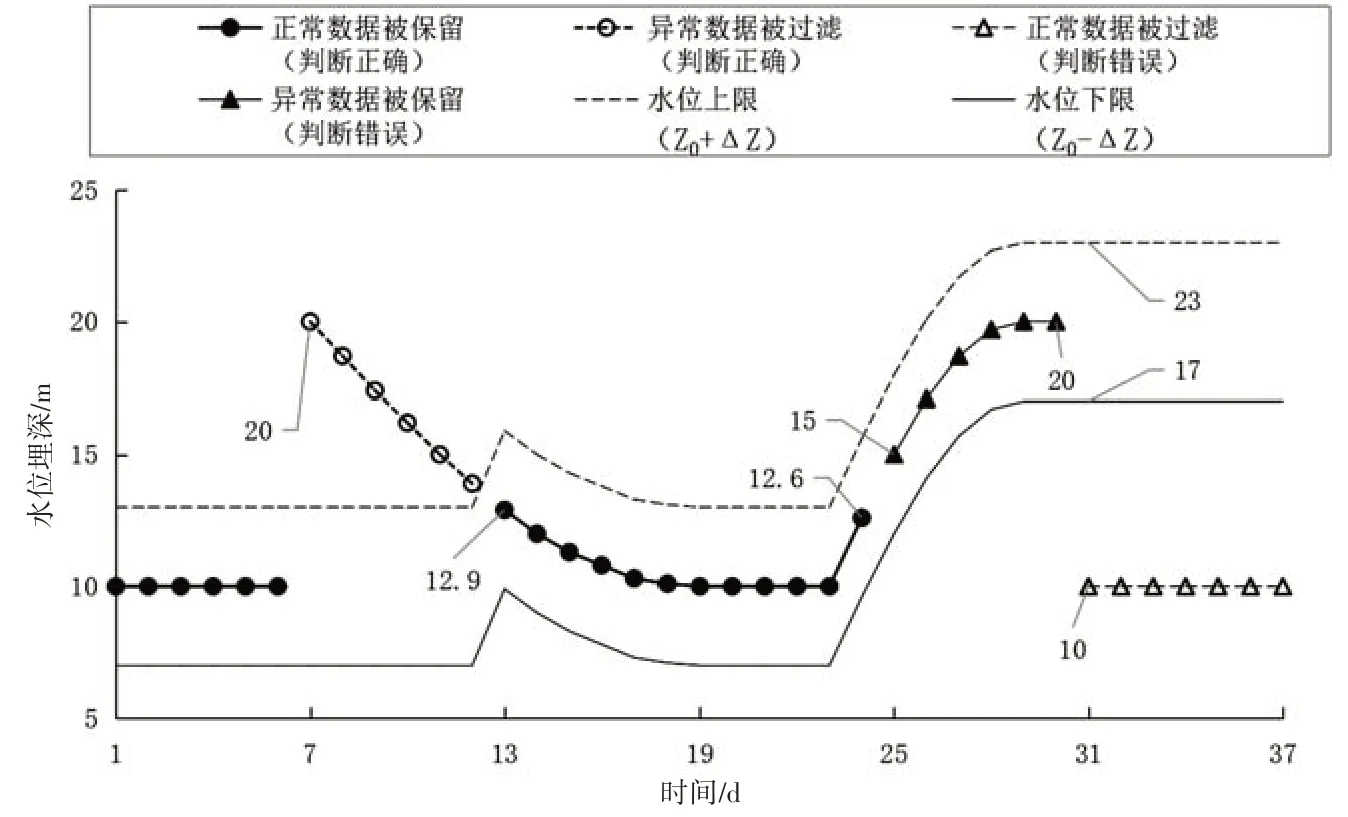
图1 原方案对某站点异常数据的过滤结果

从图1可以看出以下情况：①第7天的数据出现异常，水位达到20 m 超过上限被过滤；第13 天水位为12.9 m，处于上下限之间被保留。此处的判断是正确的。②第25 天的数据出现异常。水位从15 m开始缓慢上升，且始终保持在上下限之间。原方案认为这些数据是正常的，因此没有进行过滤，随后在第31 天将水位上下限分别拉升到23 m 和17 m。此处的判断是错误的。③第31天水位变为10 m，恢复到正常范围。原方案认为此时水位低于下限17 m并将它及之后的数据全部过滤掉。此处的判断是错误的。

在原方案中，为避免遇到②中发生的错误，需要将变幅阈值ΔZ设置的尽量小；当变幅阈值ΔZ太小时，会发生③中的错误；若设置的变幅阈值ΔZ过大，则无法过滤①中的异常数据。因此，原方案存在的不足是无法同时拦截这几类异常数据。

3 数据过滤新方案的建立

3.1 方案目标

为克服原方案的不足，新方案需要从站点特性的角度进行考虑，提取站点特性参数，以此建立阈值进行数据过滤，实现自动处理。

3.2 站点特性分类

站点特性可分为阈值参数和参照参数2 类。其中，阈值参数主要包括相对均值差、振幅、速率等，可参与数据过滤流程；参照参数主要包括相近站点、波动周期、降水、抽水灌溉情况等，可在人工复核阶段提供辅助参考。

3.3 新方案过滤规则

3.3.1 阈值参数选取

为实现数据自动处理，新方案主要选取阈值参数建立过滤规则，从而实现范围控制。阈值参数主要包括相对均值差、波动振幅和速率。

（1）相对均值差。考察实时水位数据与某一时间长度滑动平均值之间的偏差程度。这一偏差的合理区间范围计算如下式所示：

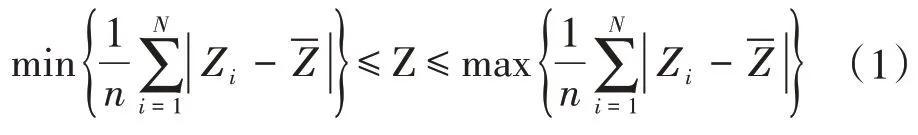
式中：n为天数（d）；N为数据系列的总天数（d）；Z为实时水位（m）；Zi为某一时间点的水位埋深（m）为水位埋深年均值（m）。

（2）波动振幅与速率。这2个参数是临近2个数据间的变化特性，考虑到历史数据的数据间隔一般是1～5 d，实时数据间隔小于1 d。为统一处理，将时间计算单位统一整合为1 d。

3.3.2 新方案的建立

新方案过滤的主要流程是根据站点特性建立过滤阈值，实时对数据进行比对分析，并对阈值进行调整。过滤时，先对多年相对极值进行判断，再对波动振幅和速率进行判断。

4 新方案与原方案过滤效果的评价分析

4.1 典型站点选取与方案应用

为对比分析2种方案的过滤效果，选取4处典型地下水代表站，即宝坻张会庄（站1）、河西物资仓库（站2）、东丽胡张庄（站3）、滨海新区南抛村（站4）。其中，站1和站2为浅层地下水站；站3和站4为深层地下水站。4 处站点均包含典型数据与非典型数据。在对比分析前，所有数据将在2 个方案中分别应用产生2组筛选结果。

一般而言，地下水位比较稳定，为更好表现2个方案在数据处理中的差异，对极值差进行分析。极值差是近1 个月内水位数据的极大值与极小值之间差距的最大值。其计算公式为：

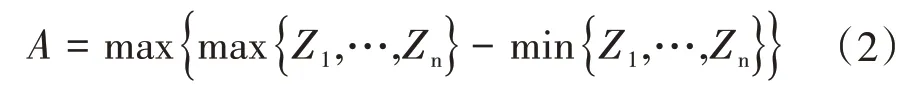
式中：A为水位极值差（m）；n为天数（d）；Z为地下水位埋深（m）。

4.2 基本统计评价

将2 组方案处理后数据的过滤量及统计参数进行对比，结果详见表1。

表1 两方案过滤后统计参数对比

从表1 可以看出以下情况：①过滤量。新方案比原方案过滤的数据少，分别为20.6%（站1）、21.56%（站2）、37.02%（站3）、26.66%（站4）。②均值。两方案的均值与原始数据都比较接近，相对差距分别为-0.05 m（站1）、0.13 m（站2）、-0.1 m（站3）、0.2 m（站4）。③标准差σ。新方案的标准差比原方案更接近原始数据，分别为0.41 m（站1）、0.14 m（站2）、0.07 m（站4）。站3的数据经原方案处理后，标准差增加了0.38 m，数据发生离散；经新方案处理后，标准差接近1 m，数据没有发生离散，表现更好。④极值差。新方案比原方案更加接近原始数据，分别为1.36 m（站1）、0.04 m（站2）、0.00 m（站4）。站3数据被原方案过滤近半，所得极值差代表性较差。

因此，新方案比原方案保留了更多的原始数据特性，与原始水位的动态过程更接近。

4.3 错误统计评价

在2 个方案处理数据时，遗漏错误数据产生的漏报越少，方案的可靠性越高；拦截正确数据产生的误报越少，方案的精确性越高。在人工复核后，两方案误报漏报的情况详见表2。

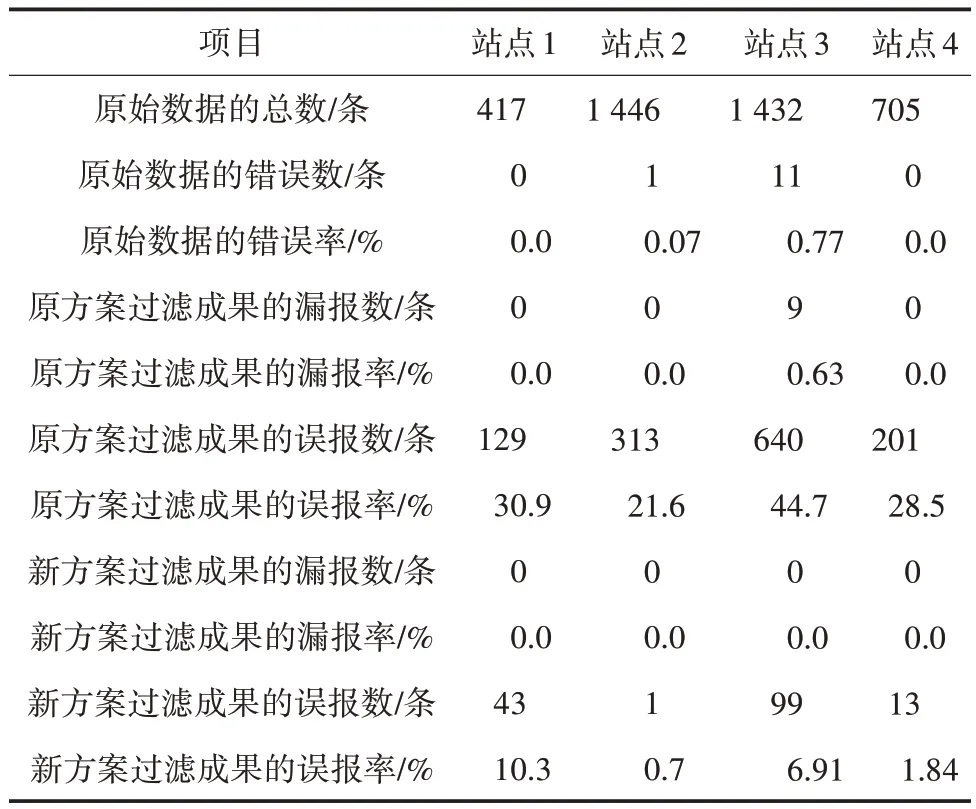
表2 两方案误报漏报统计

从表2 可以看出，新方案的漏报率和误报率均比原方案低。将站3 的原始数据（见图2）、原方案过滤结果（见图3）、新方案过滤结果（见图4）进行对比。

图2 站点3原始数据系列及错误数据位置标记

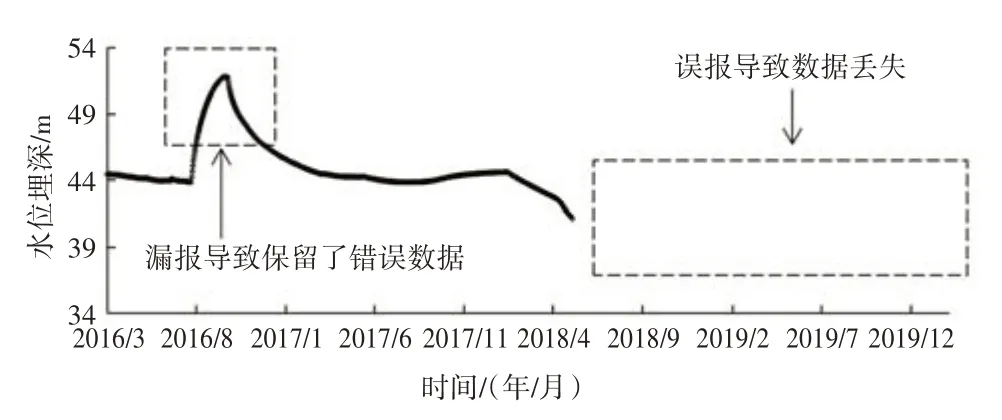
图3 站点3原方案过滤结果及数据漏报误报情况标记

图4 站点3新方案过滤结果及正确识别情况标记

由图2—4可以看到，在原始数据中，2016年8月的地下水位埋深大于49 m，为错误数据。原方案没有过滤这些错误数据，而新方案可以正确识别错误并过滤。2018年4月水位出现波动后恢复到正常水平，原方案将正常数据全部过滤，产生大量误报；新方案及时对正确数据进行了响应，有效地减少了误报。

因此，新方案可以准确判断数据是否正确，更快地响应数据变化，从而及时避免误判，相比原方案在可靠性和精确性两方面都表现更优。

5 结语

笔者首先分析了原方案数据过滤方式、错误产生原因，之后基于站点特性建立数据过滤新方案，最后从基本数据统计分析、错误统计分析2个角度对原方案和新方案的过滤结果进行比较，最终得出以下结论：新方案采取站点特性作为阈值参数比原方案保留了更多原始数据特性，提升了过滤的准确性和响应速度，实现了更低的漏报率和误报率，整体可靠性更高。