基于神经网络的燃气导流器型面优化研究

陈麒齐，姜 毅，王志浩，贾启明

(北京理工大学宇航学院，北京 100081)

0 引言

导流器作为导弹垂直发射防护装置中的重要组成部分，其作用是将燃气排导到远离导弹的方向，防止燃气射流冲击发射装置。由于导流器在发射过程中受到燃气射流的直接冲击，表面温度较高，因而需要对导流器型面进行优化设计，达到保护发射装置安全及延长导流器使用寿命的目的。目前，国内外学者对燃气射流导流器设计和优化理论与技术进行了一系列的研究。盛文成[1]通过数值模拟计算研究了不同形式的导流器对燃气流运动规律的影响。刘念昆[2]分析得出了导流锥折转半径、导流锥宽度、冲击角度和冲击高度可影响燃气流热冲击效果的结论，优化了车载发射导流装置的结构。李荣[3]采用神经网络优选方法对火炮关键参数通过区间优化得到的多个方案进行了寻优。

以车载单面导流器为研究对象，针对导流器高度、导流器折转半径、导流器背板与发射架距离3个结构参数改变引起的热环境表面温度变化进行数值研究，使用BP神经网络方法、RBF径向基神经网络方法建立了导流器型面与表面温度之间关系的代理模型并进行对比，用粒子群优化算法对RBF神经网络代理模型进行寻优，最终对优化结果用数值计算方法进行了验证。

1 理论基础

1.1 流场控制方程

流体力学遵循质量守恒定律、动量守恒定律和能量守恒定律，描述这三大守恒定律的数学方程就构成了流体力学的基本方程组[4]。

质量守恒方程：

(1)

动量守恒方程:

(2)

能量守恒方程：

(3)

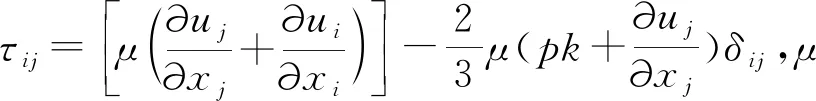
1.2 湍流模型

采用Realizablek-ε湍流模型[5]模拟燃气射流流动，相对于标准k-ε模型而言，Realizablek-ε模型能更真实地反映旋转流动、强逆压梯度的边界层流动以及流动分离等现象[6]。Realizablek-ε湍流模型关于湍动能k的输运方程为：

(4)

关于耗散率ε的输运方程为:

(5)

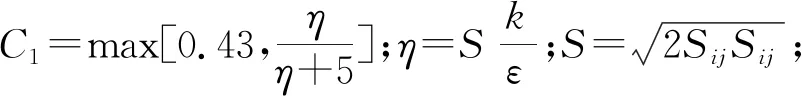
1.3 神经网络模型

采用了BP神经网络和RBF径向基神经网络建立代理模型，进一步采用RBF径向基神经网络对导流器型面进行了优化[7]。

RBF径向基神经网络由输入层、中间层和输出层构成，图1表示神经元数量为k的m输入n输出的RBF神经网络拓扑结构。RBF径向基神经网络中间层隐单元的数量与问题复杂程度相关，隐单元中采用的径向基函数常用的为高斯函数：

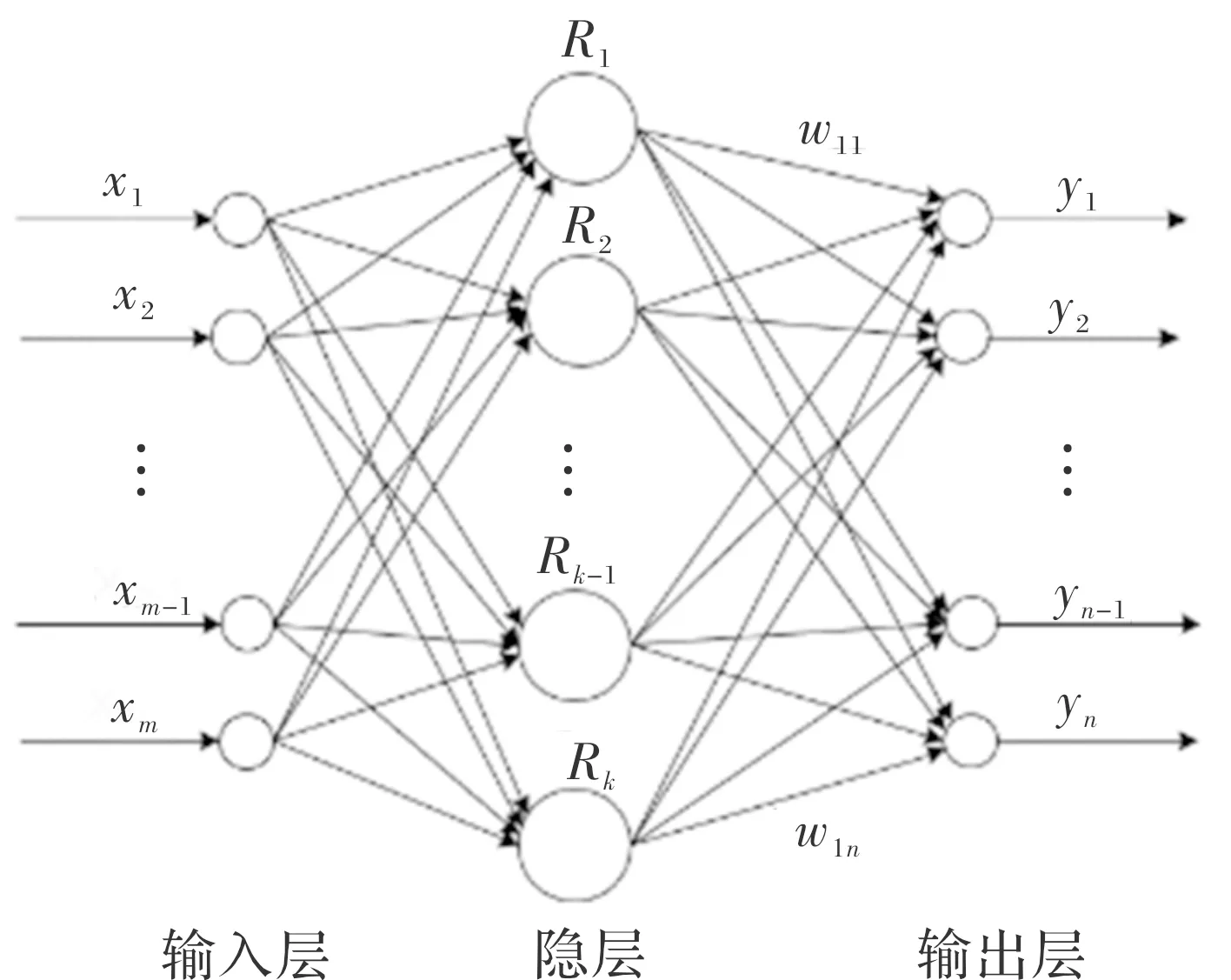
图1 径向基神经网络拓扑结构图

(6)

式中:X为输入向量，其维度为输入个数;Cj为第j个隐单元的高斯函数中心向量;‖·‖为取欧氏范数的运算;σj为该隐单元高斯函数的扩展常数。在n个输出的径向基神经网络隐含层数目为k时，其输入与输出间的关系为：

(7)

式中：ωjl为隐含层到输出层的连接权值；b为输出层阈值,l=1,2,…,n。

2 燃气导流器流场计算分析

2.1 射流计算准确性验证

为了进行射流流场仿真模型计算准确性的验证，建立发动机尾喷管向地面直接喷射燃气流的二维轴对称冲击模型进行定常计算。采用Realizablek-ε湍流模型，选择基于压力基的PISO算法，流场入口边界按照某型发动机设置为压力入口，燃烧室总温3 636.5 K、总压10.5 MPa，环境压强101 325 Pa，温度300 K。发动机内工质视为一种混合燃气，发动机及地面边界为绝热壁面，远离燃气核心区处均设置为压力出口。

图2为射流冲击流场的马赫数分布云图，可以清晰地看出燃气射流在发动机尾喷管出口附近形成了钻石型激波，燃气流在滞止区速度降为0。图3对比了文献[8]中射流冲击效应试验高速摄影图片与流场仿真计算结果的温度分布。仿真计算模拟出了在燃气流撞击地面处滞止区出现高温，随着燃气流向两边流动温度逐渐下降的现象，可以证明文中采用的计算方法得出的计算结果能够反映这一类燃气射流冲击过程流场的真实流动情况。

图2 射流冲击流场马赫数分布

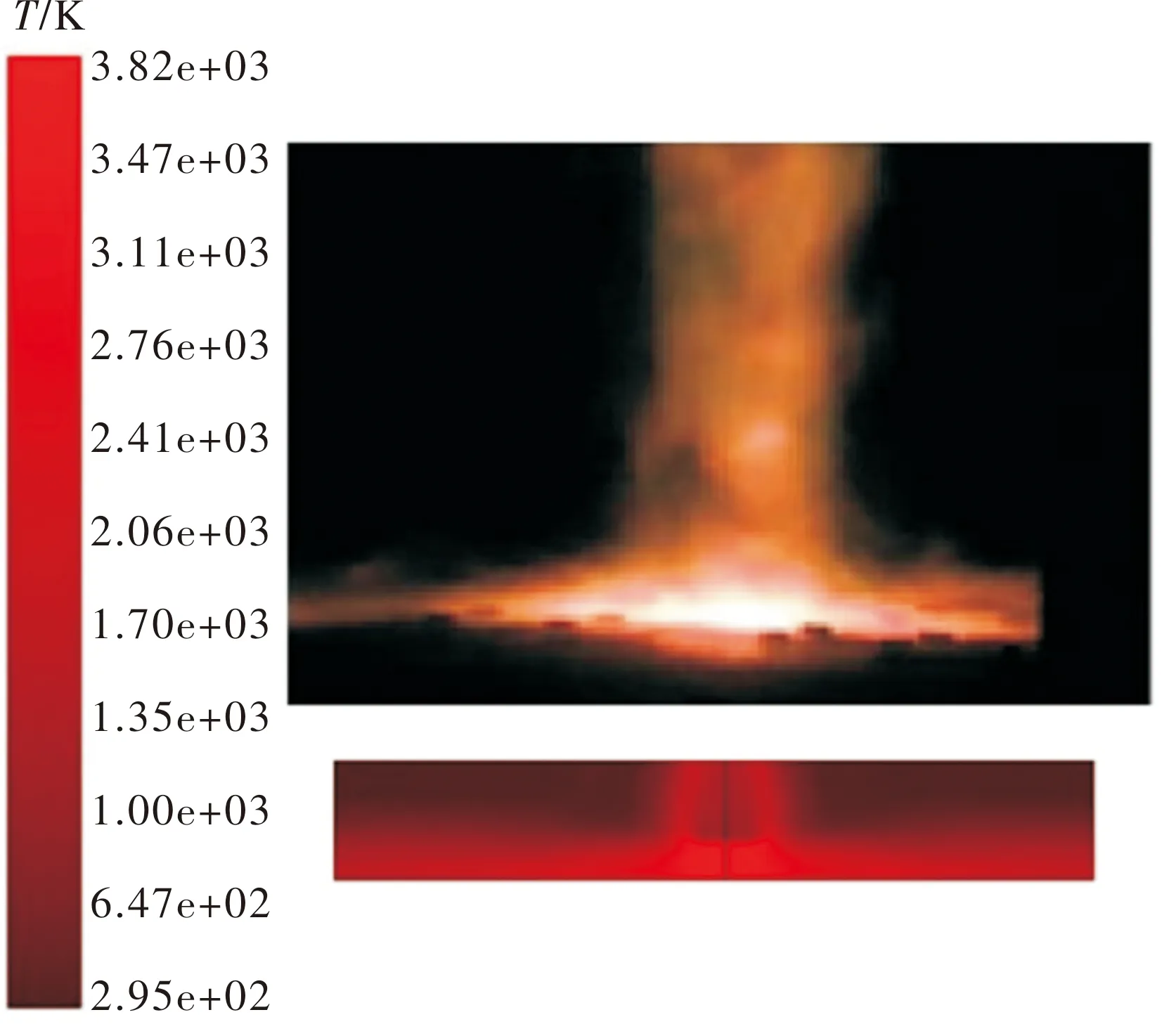
图3 射流冲击效应高速摄影与温度计算结果对比

2.2 导流器流场仿真计算

选择最接近于导弹实际发射角度的87.5°，建立由平台台架、起竖油缸、导轨、导弹和导流器组成的二分之一对称发射流场三维模型。导流器结构如图4所示。发射流场整体模型及边界条件如图5所示。发动机压力入口总温保持3 636.5 K，实时更新发动机总压进行非定常计算，以动网格形式实现导弹在流场计算域中的运动，分析导弹发射过程中燃气射流对于导流器的动态影响过程。

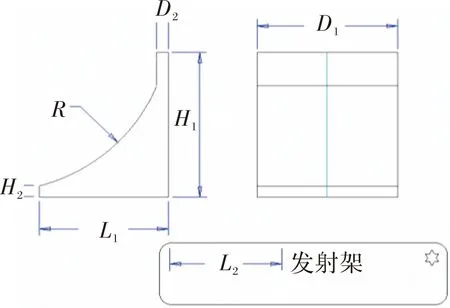
图4 导流器结构模型

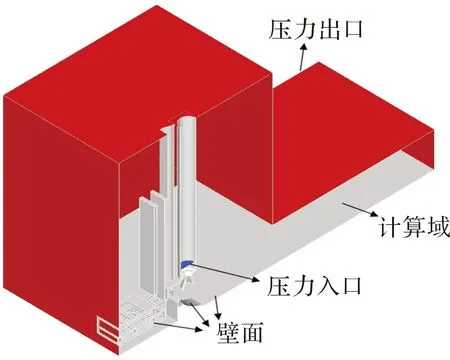
图5 流场整体模型及边界条件

图6所示是导流器表面温度最大值的时间曲线。燃气流初始冲刷导流器时造成导流器表面最高温度瞬时升高，由于射流流动出现短暂降低，然后逐渐升温至最高接近3 600 K，在导弹未开始运动前趋于平稳。随着导弹沿着导轨逐渐远离地面，导流器表面温度逐渐下降，但受燃气流影响的区域面积有所增大，高温区域上移。

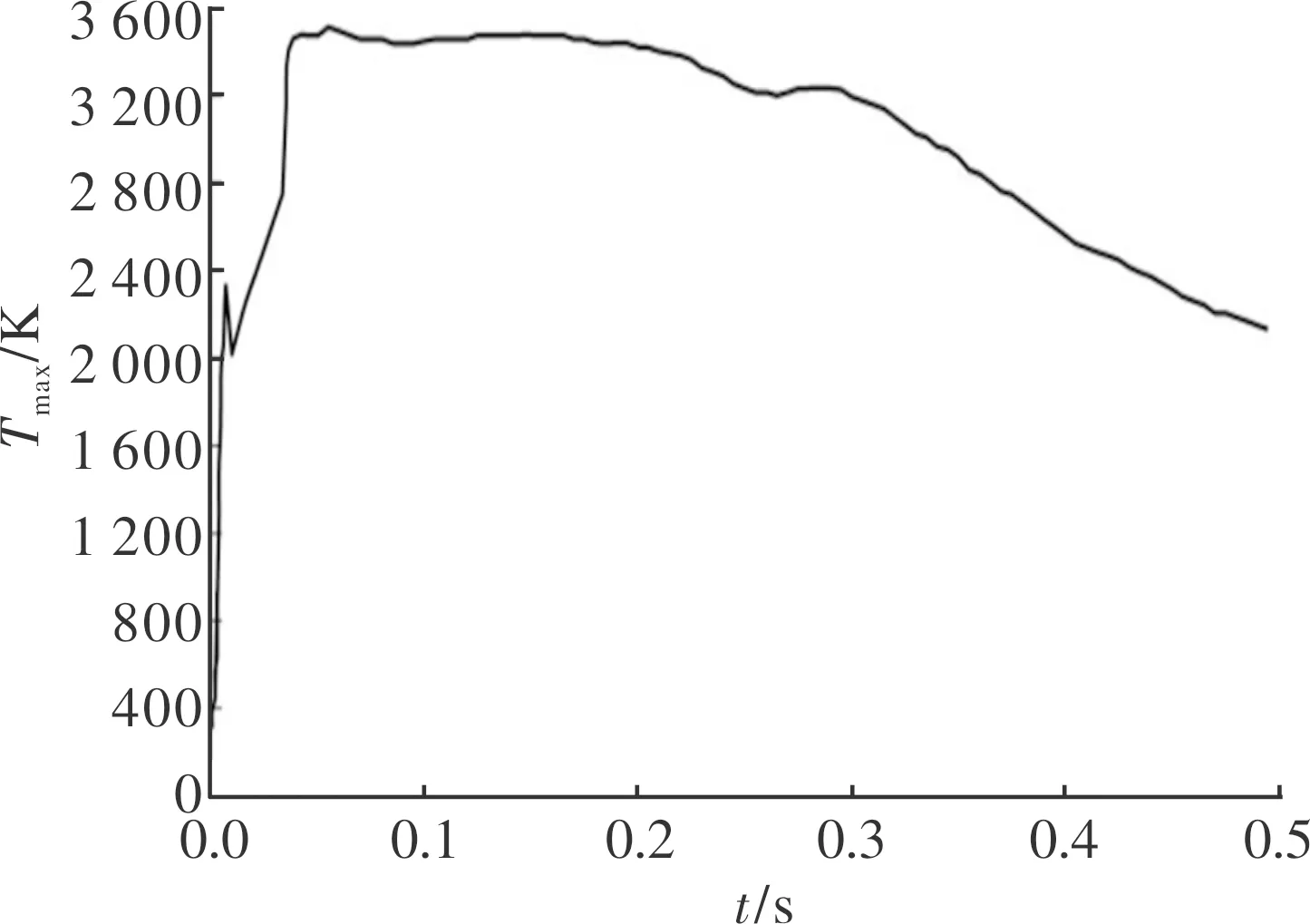
图6 导流器表面温度最大值

2.3 导流器流场影响参数分析

根据导流器流场仿真结果及工程经验，发动机喷管出口与导流器的相对距离、导流器形状以及相对发射架之间的几何关系等结构参数对导流器的导流效果和热环境有很大影响。对导流器长度L1、导流器背板距发射架的水平距离L2及导流器折转半径R三个几何参数对导流器流场的影响程度进行分析，基准模型说明见图4。分析影响程度的评价标准参考文献[9]，以温度-时间积分作为热环境特性的评价指标：

(8)

式中:Tmax为导流器表面最高温度;t0为燃气流初始冲刷到导流器表面的时间点;Δt为监测时间。Δt根据导弹未开始运动的时间选取为0.03 s。

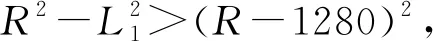
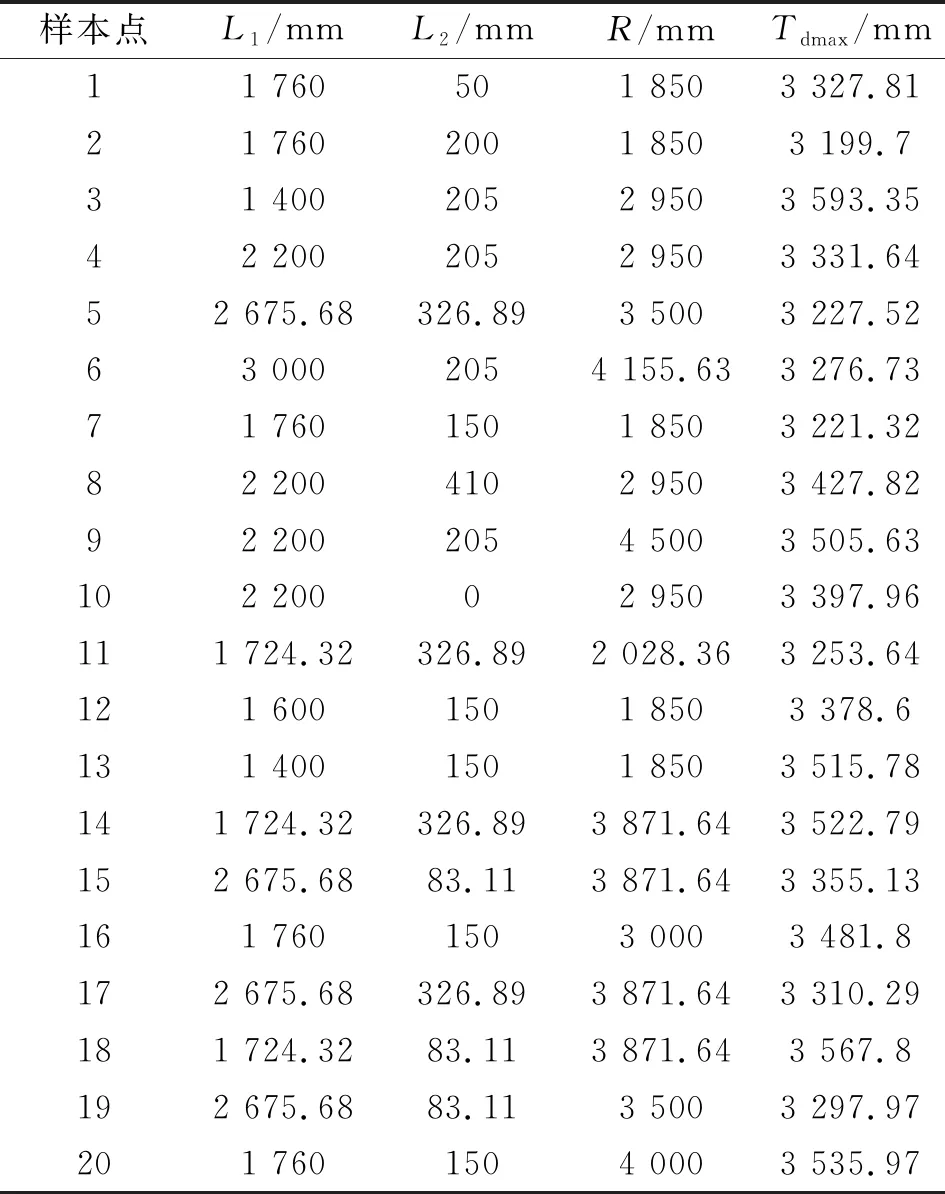
表1 3个参数样本点与输出响应

基于输入输出数据，进一步建立多项式响应面近似拟合分析[11]，得到分别确定L1=2200 mm以及R=3000 mm时，另外两个参数对导流器表面热环境评价指标的影响如图7所示。

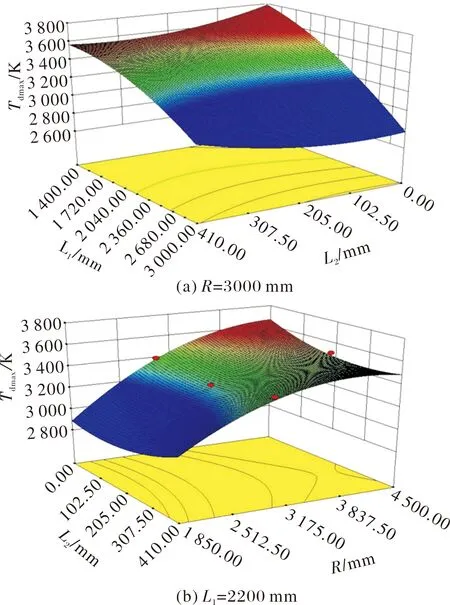
图7 导流器表面热环境响应面

可以看出，随着L1的减小及R的增大，导流器表面热环境评价值变大，导流器受热冲击程度加剧；L2与导流器受热冲击的程度在L2接近250 mm前负相关，超过后正相关，呈现出近似于抛物线性质的关系。

3 燃气导流器型面优化

3.1 神经网络模型对比分析

基于2.3节影响参数的分析结果，选择三参数作为优化参数，以优化导流器的表面热环境作为目标，同时为了满足机动性要求将导流器体积作为优化限制条件之一。

分别建立3个优化参数下的BP神经网络代理模型和RBF神经网络代理模型，对导流器流场热环境进行预测优化并对比分析。经过多次试验，采用5个隐含层神经元，建立导流器的BP神经网络代理模型；选取适当的学习算法求解待定参数Cj，σj，ωjk，确定散布常数为0.5[12]，建立导流器的RBF神经网络代理模型。采用归一化处理后的三参数样本数据进行学习，两种神经网络代理模型训练过程的误差曲线如图8所示。

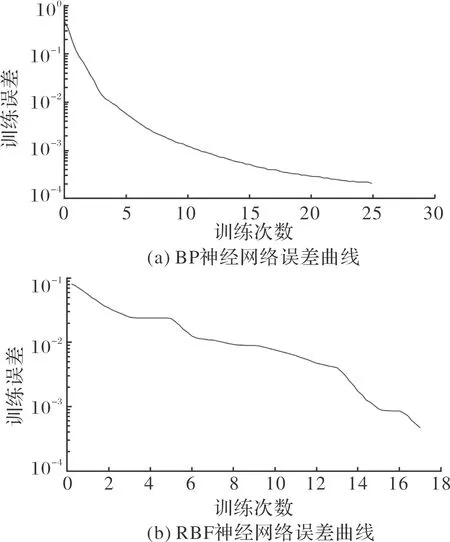
图8 两种神经网络模型误差曲线

BP神经网络建模的决定系数为0.954 2，RBF神经网络的建模结果决定系数为0.995 3。此外，BP神经网络预测过程的稳定性不佳，因此，决定采用RBF径向基神经网络代理模型进行燃气导流器型面的进一步优化。

3.2 优化结果及流场验证分析

利用PSO粒子群优化算法对导流器热环境评价指标和体积进行多目标优化[13]，通过RBF神经网络模型进行优化的结果如表2所示，其中V是导流器体积，εT是经过数值仿真验证得到的值与代理模型值之间的误差。

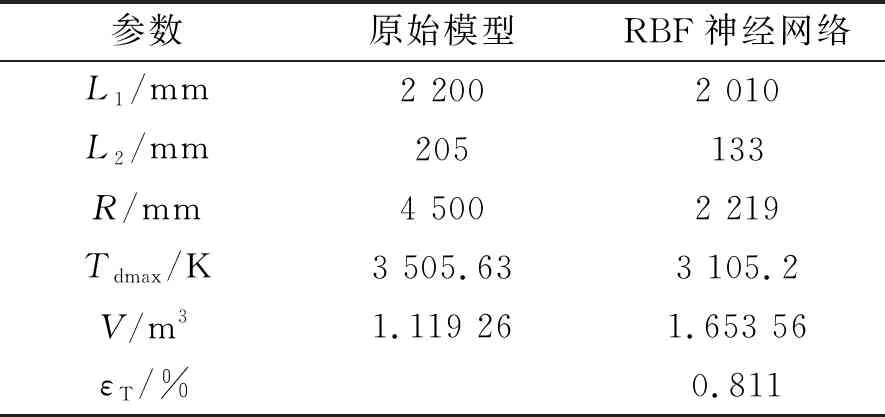
表2 原始模型与优化结果

基于RBF神经网络代理模型优化结果参数，建立相应的导流器三维模型进行流场仿真计算验证。原始模型和RBF神经网络优化模型的导流器表面温度分布如图9所示，两种模型的燃气流场温度分布如图10所示。导流器表面温度最大值与时间的关系如图11所示。

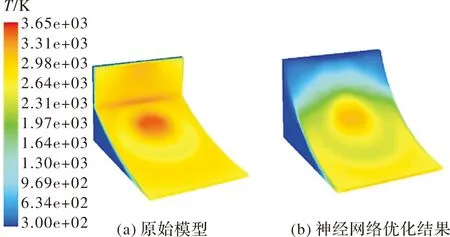
图9 导流器表面温度分布优化前后对比图

图10 燃气流场温度分布图

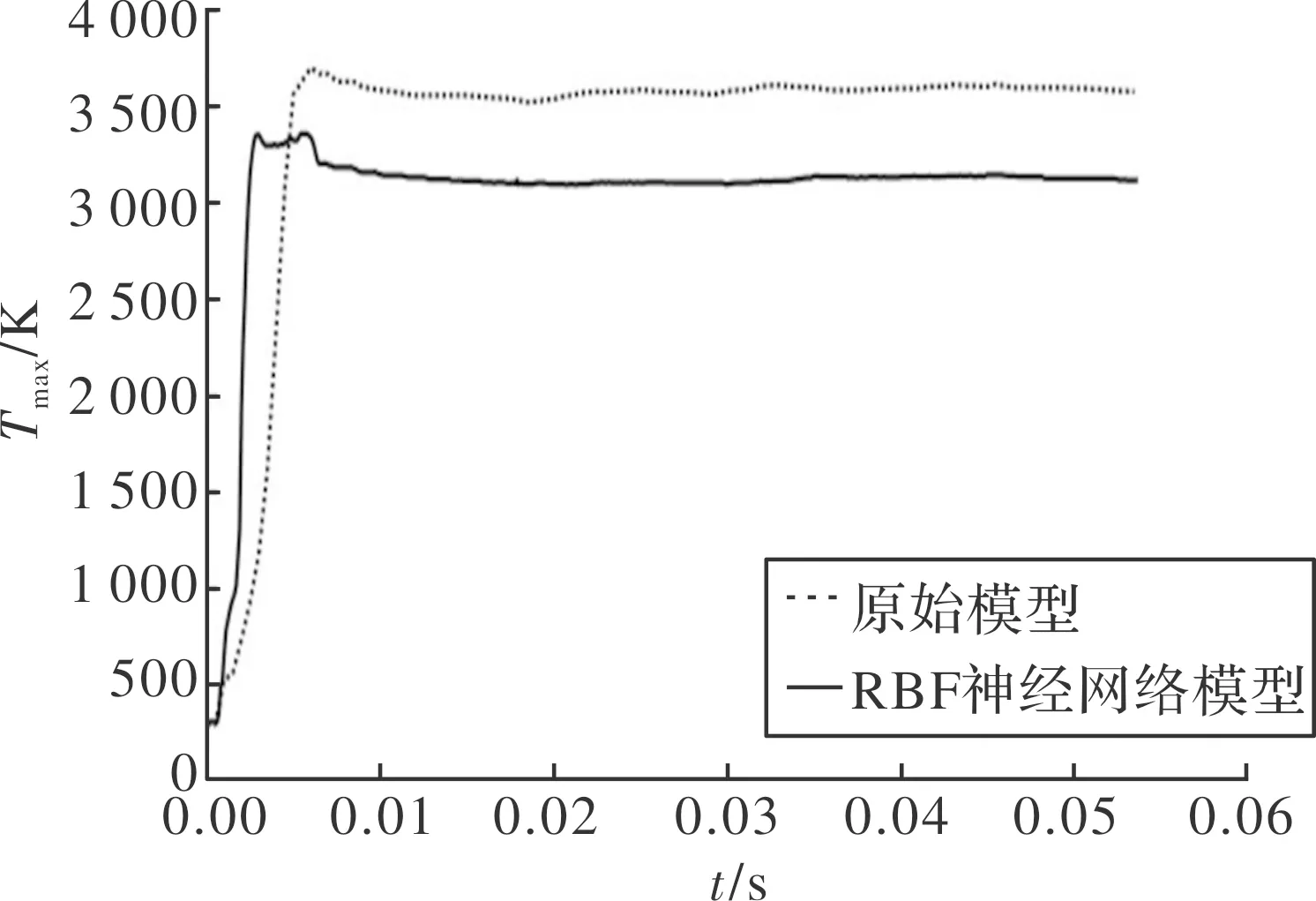
图11 导流器表面温度最大值与时间的关系图

可以看出，经过优化后，在导流器体积满足机动性要求的前提下，导流器表面的最大温度3 105.2 K，明显降低约400 K，导流器表面的整体温度下降，高温区面积减小，热环境得到优化，且导流效果比优化之前更好。优化误差为0.811%，在1%之内，验证了该神经网络模型的准确性。

4 结论

1)随着L1的减小及R的增大，导流器受热冲击程度加剧；L2与导流器受热冲击的程度在L2接近250 mm前负相关，超过后正相关。

2)经过流场计算验证，基于RBF神经网络代理模型的三参数优化，能使导流器表面温度下降约400 K，导流器热环境得到明显改善，能完成燃气排导的设计目的，计算误差在1%之内。