基于AI-AP-PHD滤波的多目标跟踪方法

谭顺成，韩芳林，于洪波

(1 海军航空大学信息融合研究所, 山东烟台 264001;2 南京电子技术研究所, 南京 210039)

0 引言

基于随机有限集理论的概率假设密度(probability hypothesis density，PHD)滤波也称为一阶矩滤波，由Mahler于2000年首次提出[1]，是一种Bayesian框架下的近似多目标滤波方法，其核心思想就是通过递推更新多目标后验概率密度的第一阶统计矩，来代替递推更新多目标全局后验概率密度，从而极大降低了多目标跟踪问题的复杂程度，非常适应于杂波环境下的多目标检测与跟踪，并被成功地用于解决许多工程问题[2-4]。根据实现方式不同，PHD滤波主要可以归为两类：粒子PHD(particle-PHD，PPHD)滤波[5-6]和高斯混合PHD(Gaussian mixture PHD, GM-PHD)滤波[7-8]。其中，PPHD滤波方法由于在非线性非高斯情况下的多目标跟踪方面具有较好的适应性，得到越来越多的重视，文献[9]将辅助粒子滤波(auxiliary particle filter，APF)的思想引入PPHD滤波，通过在高维空间进行采样，使PPHD滤波更加高效。

然而，传统的PHD滤波一般只利用了目标的距离、方位和多普勒等信息(即门限处理后的量测)，而如雷达和红外等很多的传感器，除可提供目标的上述信息，还能提供目标回波信号的强度或幅值等信息。由于目标的回波信号在各时刻具有强相关性，而杂波具有非相关性，若充分利用目标的幅值信息，一方面可强化目标和杂波区别，在滤波过程中尽早的识别出目标和杂波，从而有效改善目标跟踪效果；另一方面，可使目标航迹的形成不仅仅基于目标运动的一致性，还可基于目标回波的相关性，从而有效改善数据互联性能，减少虚假航迹[9-10]。文献[10]将目标的幅值信息引入概率数据互联(probabilistic data association，PDA)滤波，有效改善了杂波环境下的单目标跟踪性能。此外，将目标幅值信息引入目标检测和跟踪，还可有效改善低信噪比情况下的目标检测跟踪性能，是检测前跟踪(track-before-detect，TBD)方法的必经步骤[11]。

基于上述考虑，充分利用目标的幅值信息，构造一种结合目标幅值信息的辅助粒子PHD(AI-AP-PHD)滤波方法，以解决杂波环境下的多目标跟踪问题，仿真结果表明该方法性能优于传统的PHD滤波方法。

1 量测模型

由于量测可能源于目标或杂波，目标检测可描述为窄带高斯噪声条件下慢瑞利幅度调制的窄带信号的假设检验问题[10]：仅有噪声(H0)和存在目标 (H1)。

(1)

杂波和目标幅度的概率密度函数分别为:

(2)

和

(3)

式中：a为杂波或目标幅值；σ2=N0T/4为平均噪声能量;N0为接收到的单边带噪声功率谱密度，T为脉冲间隔；整个脉冲间隔T上的能量ST为：

(4)

式中：d为非对数形式的SNR的期望值,使d=ST/N0。不失一般性，假设噪声协方差σ2=1，那么式(2)和式(3)可写成:

(5)

和

(6)

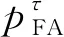
(7)

和

(8)

当目标信噪未知时，假设信噪比在区间[SNRmin,SNRmax]成均匀分布，其中SNRmin和SNRmax分别表示信噪比可能的最小和最大值。依据定义，d=10SNR/10，非对数形式的信噪比的分布函数为:

(9)

其中:

(10)

(11)

(12)

2 AI-AP-PHD滤波算法实现

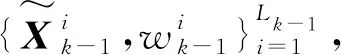
(13)

其中:

(14)

(15)

(16)

(17)

(18)

(19)

(20)

(21)

其中:κk(z)为杂波分布;Rk为量测误差协方差;(xs,ys)为传感器的坐标。

1)计算所有粒子的权重和：

(22)

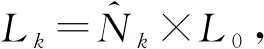
步骤3：粒子集更新。

2)更新粒子权重:

(23)

并进行归一化处理：

(24)

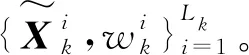
步骤4：多目标状态估计。

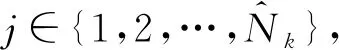
(25)

3 仿真分析

3.1 场景设置

不失一般性，考虑一个二维的仿真场景(仿真参数和仿真结果中，如未做特别说明单位均为归一化的单位)，传感器的观测区间为S=[-200,200]×[-200,200]，任意时刻，目标和杂波可在该区间内随机出现和消失，且目标的运动均符合线性高斯模型:

(26)

其中:

(27)

(28)

N(·|X0,Qb)为均值为X0和方差为Qb的正态分布。

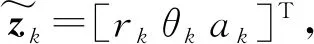
(29)

其中:w1,k和w2,k为相互独立的零均值高斯噪声，且与过程噪声相互独立，其标准差分别为2和0.05;w3,k接近于0。杂波均匀分布在监测区域内，每帧的杂波率λk=μPFA，其中μ=50为门限前的量测个数。

3.2 仿真结果

图1为目标平均信噪比为15 dB、虚警率为0.1时，仿真产生的目标幅度信息，图2和图3分别给出了传统PHD滤波方法和文中的AI-AP-PHD滤波方法仿真结果对比，其中图2(a)和图3(a)为两种各时刻估计的目标数与真实目标数对比，而图2(b)和图3(b)则为各时刻估计的目标位置与真实的目标位置对比。

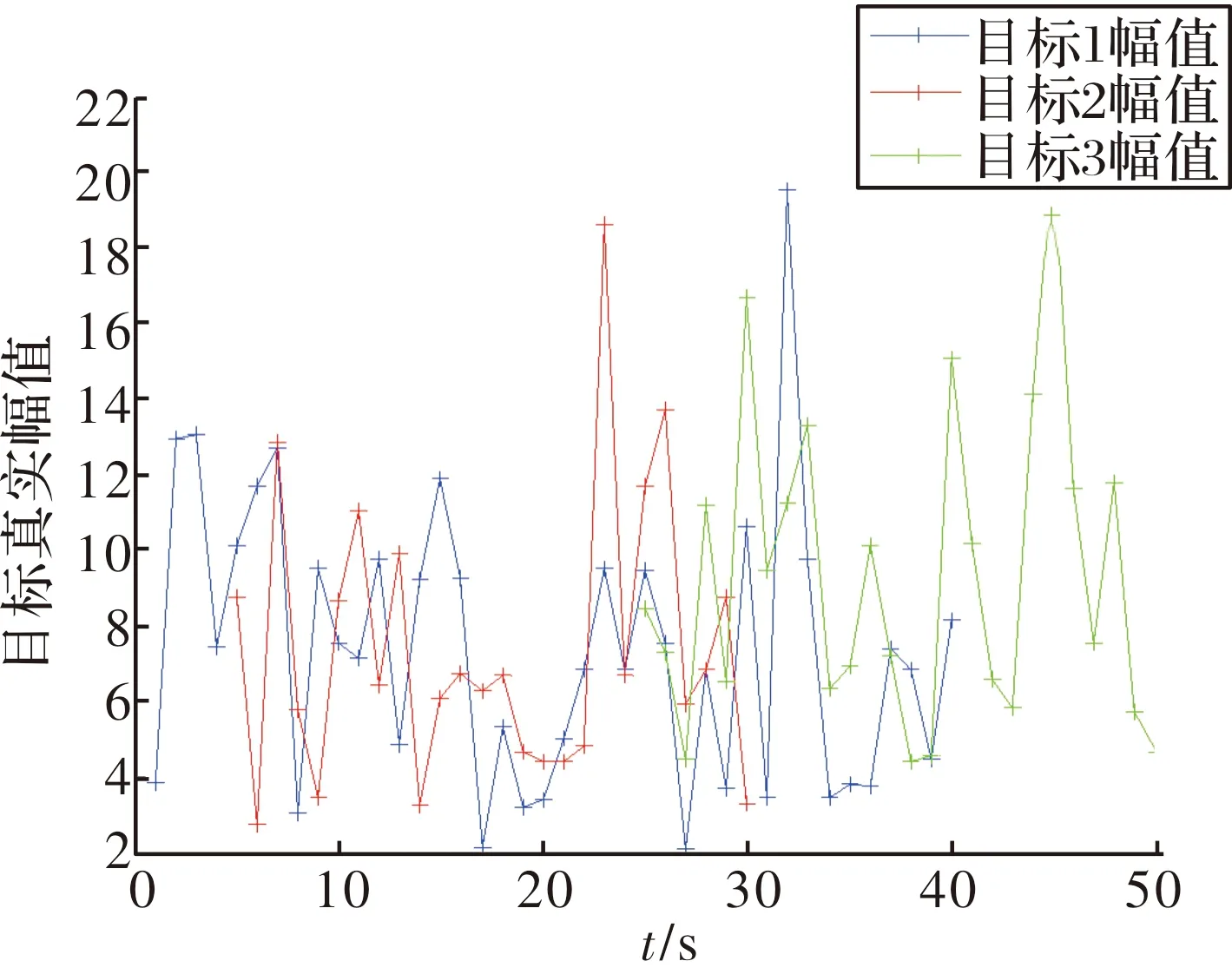
图1 目标幅值(SNR=15 dB，PF=0.1)

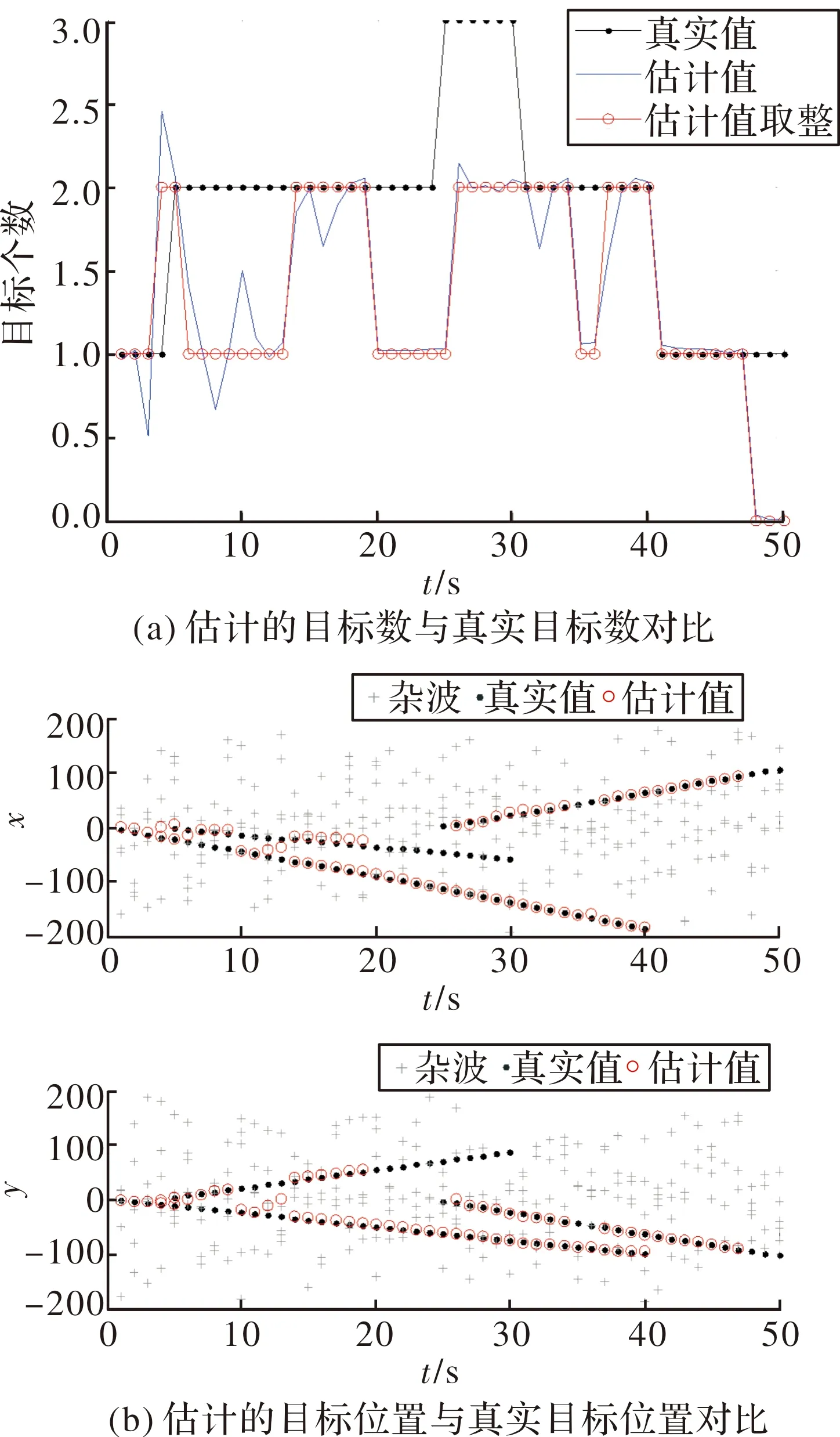
图2 PHD滤波仿真结果

为评估多目标跟踪效果，以最优子模式分配(optimal subpattern assignment,OSPA)距离作为评价指标，其综合考虑了目标定位误差和数量估计误差[12]，图4为两种方法的多目标跟踪误差对比。

从图2可以看出，传统的PHD滤波方法在估计目标数时出现较大的偏差，在较多的时刻均出现了目标漏检甚至丢失的问题，而AI-AP-PHD滤波方法只在个别时刻出现了漏检或虚警，目标正确检测概率明显优于未结合目标幅度信息的PHD滤波方法。此外，如图4所示，除第41 s外，其余时刻AI-AP-PHD滤波方法的多目标跟踪误差明显优于PHD滤波，由图3可知，该时刻AI-AP-PHD滤波并未出现漏检或虚警，目标跟踪结果也正常，该时刻多目标跟踪误差突然增大是因为OSPA计算多目标误差时目标真实状态与估计状态匹配错误，并非算法本身问题。因此，通过结合目标的幅值信息，确实可以有效改善目标的检测跟踪性能。

图3 AI-AP-PHD滤波方法仿真结果

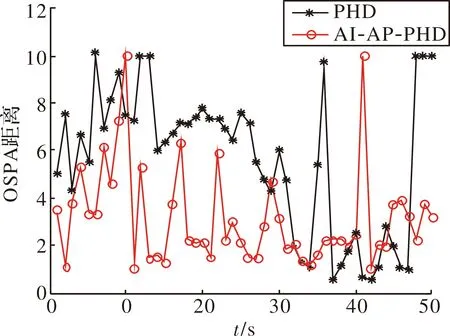
图4 两种方法的多目标跟踪误差对比

4 结论

针对杂波环境下的多目标跟踪问题，充分利用AP-PHD滤波的优势，结合目标的幅值信息，构造一种杂波环境下的AI-AP-PHD滤波方法。仿真结果表明，与传统的PHD滤波方法相比较，文中方法可以明显降低目标漏检概率，从而有效改善多目标的检测跟踪性能。下一步应对多目标跟踪评估准则进行适当的调整，以使其能更加准确反映真实的多目标跟踪误差。