考虑卸荷变形模量的坑底回弹变形计算方法

陈 晓, 董建华, 董和平, 汤小林, 田文通

(1 .甘肃建投土木工程建设集团有限责任公司, 甘肃 兰州 730050;2. 兰州理工大学 土木工程学院, 甘肃 兰州 730050)

0 引言

随着我国城市化发展,城市地下空间的开发利用成为了城市建设发展的一个重要方面[1],尤其是城市地下轨道交通迅速发展,使得建(构)物基坑工程越来越紧邻已有地铁盾构隧道,甚至有些基坑工程横跨已建地铁盾构隧道。地铁盾构隧道上方基坑的开挖,造成坑底土体在竖向卸荷作用下产生竖向隆起变形,过大的竖向位移会致使已建地铁盾构隧道的管片错位开裂,甚至影响隧道结构的安全和地铁的正常营运。《城市轨道交通安全保护区施工管理办法(暂行)》规定:隧道结构绝对沉降量及水平位移量≤20 mm(包括各种加载和卸载的最终位移量)。因此,考虑卸荷作用下的基坑变形计算方法是亟待解决的重要工程问题。

目前,预测基坑回弹变形的方法主要有分层总和法[2-3]、残余应力法[4]和数值分析法[5]等。其中分层总和法因其具有计算简单、力学参数获取方便等特点而被工程广泛应用。然而在规范分层总和法中,土体中附加应力的计算通常以Boussinesq解为基础,其计算结果往往大于实测值[6]。在基坑开挖工程的附加应力计算中,考虑荷载作用于半无限弹性体内部的Mindlin解被认为更符合实际,与此同时,大量的试验研究表明[7-9],卸荷应力路径下,土体的应力-应变特性与加载应力路径作用下有较大差别。基坑在开挖过程中,土体的回弹模量随着土体应力路径的改变而发生变化,而规范分层总和法中采用的固定的土体回弹模量计算坑底的回弹变形与基坑实际分布开挖的特征不符。

为了更合理计算考虑隧道卸荷作用下基坑开挖引起的坑底隆起变形,本文基于Mindlin[10-11]解附加应力公式,通过在基坑开挖面上进行积分,得到均布荷载作用下坑底土体附加应力计算公式,并考虑土体在卸荷应力路径作用下回弹模量的非线性变化,计算了基坑开挖引起的坑底隆起变形值。

1 卸荷引起的坑底附加应力的计算

建立计算模型,如图1所示。以矩形基坑平面中心为坐标原点建立直角坐标系,基坑开挖深度为d,长度为L,宽度为B,嵌固深度为d0,围护结构长度为H(H=d+d0)。

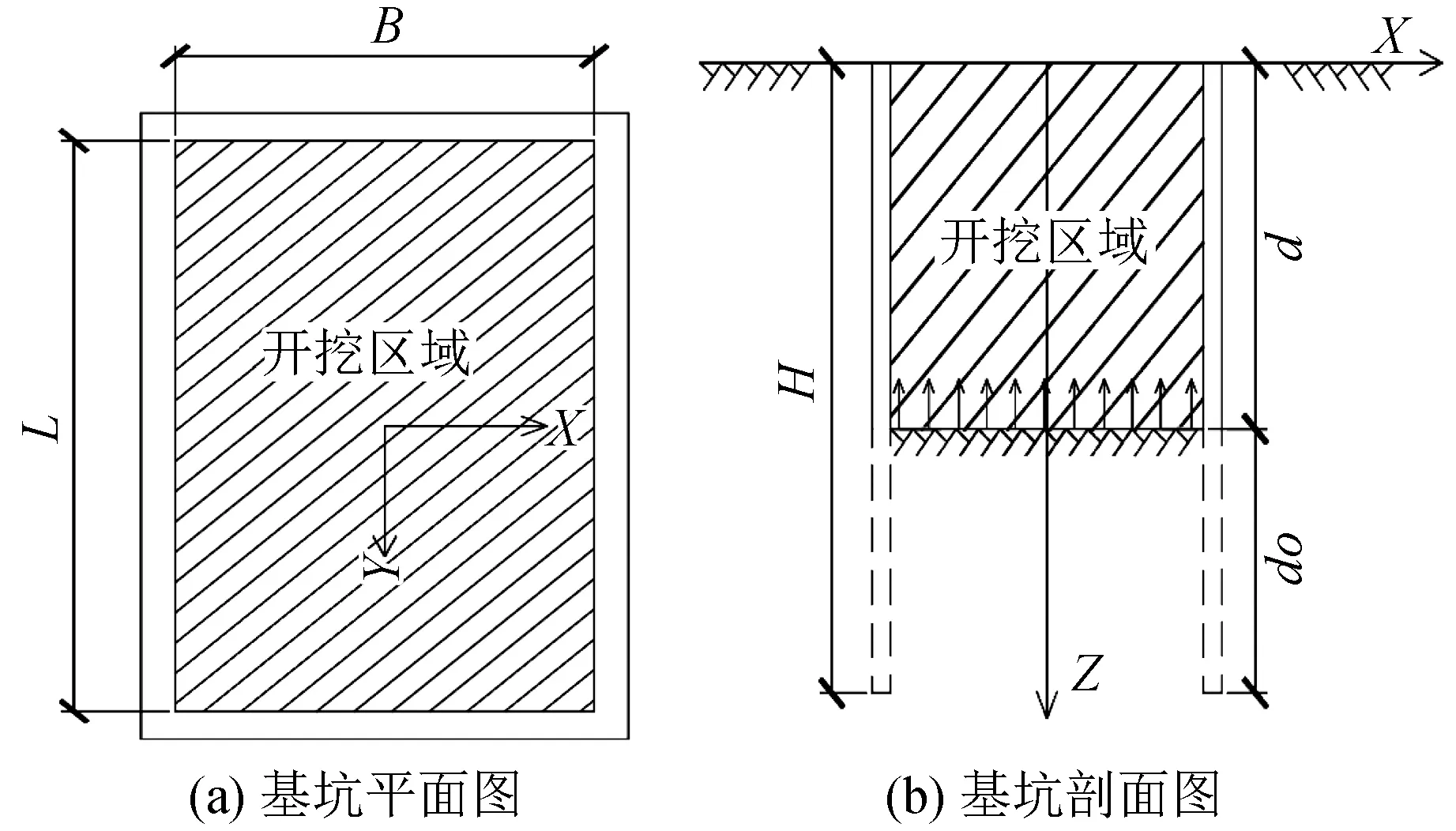
图1 基坑开挖引起坑底回弹计算模型Fig.1 Calculation model of bottom rebound caused by excavation of foundation pit

计算假定:(1)土体为均质、各向同性的半无限空间弹性体;(2)不考虑基坑开挖的时间和空间效应,只考虑基坑开挖引起的附加应力;(3)基坑开挖过程中不考虑降水作用,土体中不存在渗流;(4)当基坑开挖完成后土体应力释放,等效为在坑底开挖面处施加竖直向上的均布荷载;(5)不考虑支护结构的存在对附加应力计算的影响。

1.1 坑底卸荷分析

基坑开挖之前,坑内拟开挖土体对坑底以及侧壁分别产生竖向均布荷载σz0=γd(其中γ为土体重度,d为基坑开挖深度)和三角形分布荷载σh0=K0γd(K0为静止土压力系数,且K0=1-sinφ,φ为土体有效内摩擦角),土体在初始地应力作用下保持平衡。基坑开挖后,由于坑内土体移除,基底的竖向土压力及侧壁的水平向土压力撤除,坑底土体竖向完全卸荷,卸荷量为γd。

与此同时,基坑的开挖往往是在支护结构施作完成或开挖与支护的同步条件下进行,因此在计算基坑开挖卸荷作用引起的坑底附近土体的附加应力作用时,应当考虑支护结构的遮拦效应,即坑底卸荷应力的释放会受到支护结构与土体之间摩阻力影响。该侧摩阻力的计算表达式为[12]:

qs=c′+K0σztanφ′

(1)

式中:qs为单位等效实体侧摩阻力;c′为土体与支护结构之间黏聚力;φ′为土体与支护结构之间的外摩擦角,其取值为c′=(0-2)c/3,φ′=(0-2)φ/3,其中c、φ为土体的黏聚力和内摩擦角[13];σz为基坑开挖面到围护结构底面处的竖向应力。

根据基坑的分层开挖工况,为了便于计算,应将上述侧摩阻力表达式采用平均侧摩阻力进行表示为:

(2)

式中:q′s修正后的单位等效实体侧摩阻力;γ为开挖土体的重度;d为基坑开挖深度;H为围护结构深度。

则基坑开挖后,考虑土体开挖后的残余应力以及支护结构的摩阻力的卸荷应力值为:

(3)

式中:σi为基坑开挖引起坑底第i层土体附加应力值;B为基坑开挖的宽度;L为基坑开挖的长度;其余参数与图1中标注相同。

1.2 坑底卸荷附加应力计算

土体内部作用竖向集中力时引起的附加应力的计算公式早在1936年由美国学者Mindlin推导得到,后来一些学者在该公式的基础上通过积分获得了半无限弹性地基内部作用矩形均布荷载和条形均布荷载作用下的竖向附加应力公式,其中矩形均布荷载作用在半无限弹性体内部时竖向附加应力表达式为:

(4)

式中:B和L分别为矩形荷载的宽度和长度;c为荷载作用深度;z为计算点深度;μ为泊松比;pi为分步卸荷强度,在卸荷条件下方向朝上,数值等于开挖土方的自重,如图2所示。

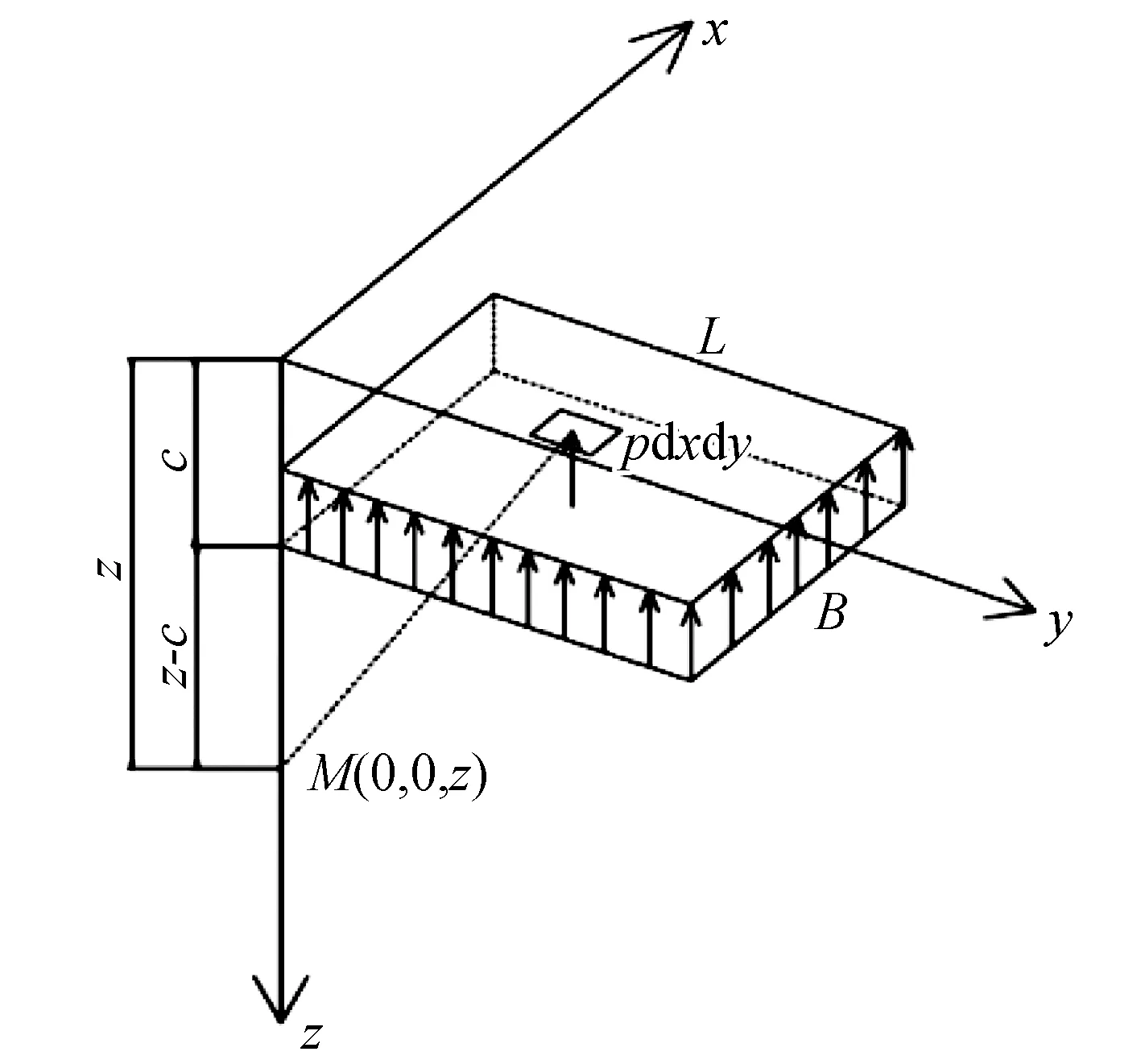
图2 矩形均布荷载条件下附加应力计算模型Fig.2 Calculation model of additional stress under rectangular uniform load

为了计算简便,可以将上式简化表示成为卸荷影响系数与卸荷力之间的关系,即为:

σzi=αiσi

(5)

式中:αi卸荷影响系数;σi为竖向卸荷应力。

1.3 矩形基坑开挖卸荷附加应力的分析

基于Mindlin公式,可以利用角点法来计算基坑分层开挖作用下坑底土体附加应力的分布特征。假设基坑开挖深度为10 m,开挖面积为24 m×24 m,土体重度为20 kN/m3;泊松比μ=0.2。开挖方式为一次性开挖卸荷,卸荷应力为矩形均布应力,下面依次分析矩形基坑开挖卸荷附加应力系数沿坑底以下土体深度方向的变化特征。

由图3可知,矩形基坑开挖卸荷作用下,采用Mindlin(明氏解)和Boussinesq(布氏解)应力公式计算的附加应力在坑底以下土体沿深度的增加均逐渐减小,但采用布氏解计算的附加应力系数明显大于明氏解,且布氏解沿深度方向的递减速率较明氏解大。

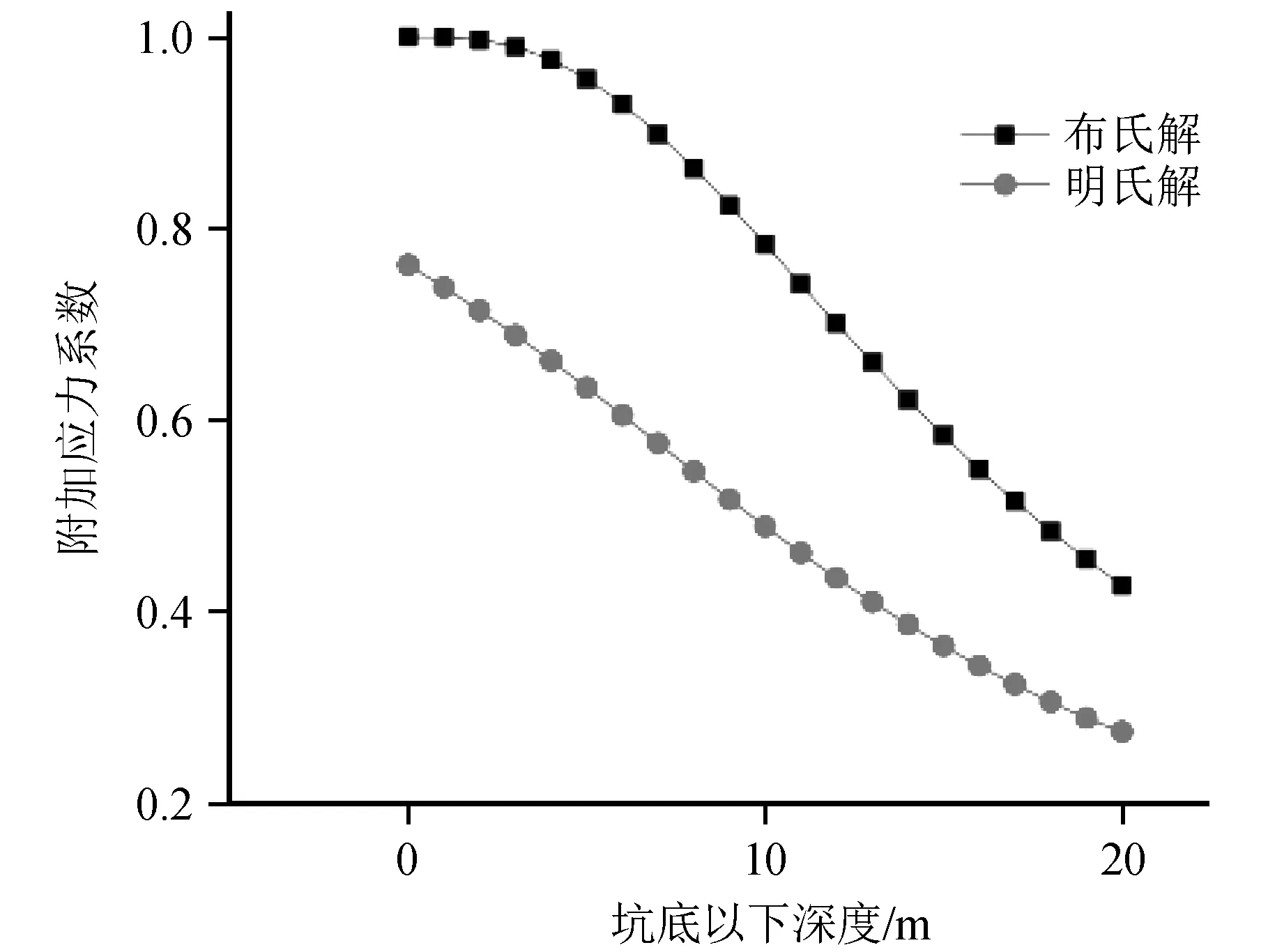
图3 布氏解与明氏解在坑底以下的分布Fig.3 Distribution of Mindlins formula and Boussinesqs formula below the pit bottom

由图4(a)可知,矩形基坑开挖卸荷引起的附加应力系数随着土体泊松比μ的变化而变化,随着土体泊松比μ的增大卸荷附加应力系数逐渐增大,但卸荷附加应力系数沿着坑底以下土体的变化趋势一致。

由图4(b)可知,卸荷附加应力系数与基坑开挖面积有关,随着基坑开挖面积越大,则基坑开挖卸荷影响范围越大,且开挖引起的坑底土体的附加应力也越大,卸荷附加应力系数随着基坑开挖卸荷量的增大而增大,基坑开挖卸荷量越大,其卸荷附加应力系数沿坑底以下土体的减小速率越慢。

由图4(c)可知,矩形接坑开挖卸荷引起的附加应力系数与基坑形状有关,不同基坑开挖形状在基坑开挖面以下土体的卸荷附加应力也不同,其中正方形基坑开挖卸荷附加应力系数大于长方形基坑开挖卸荷附加应力系数,且正方形基坑开挖卸荷附加应力系数沿坑底以下土体的减小速率大于长方形基坑,但两者沿基坑坑底以下土体的变化趋势一致。

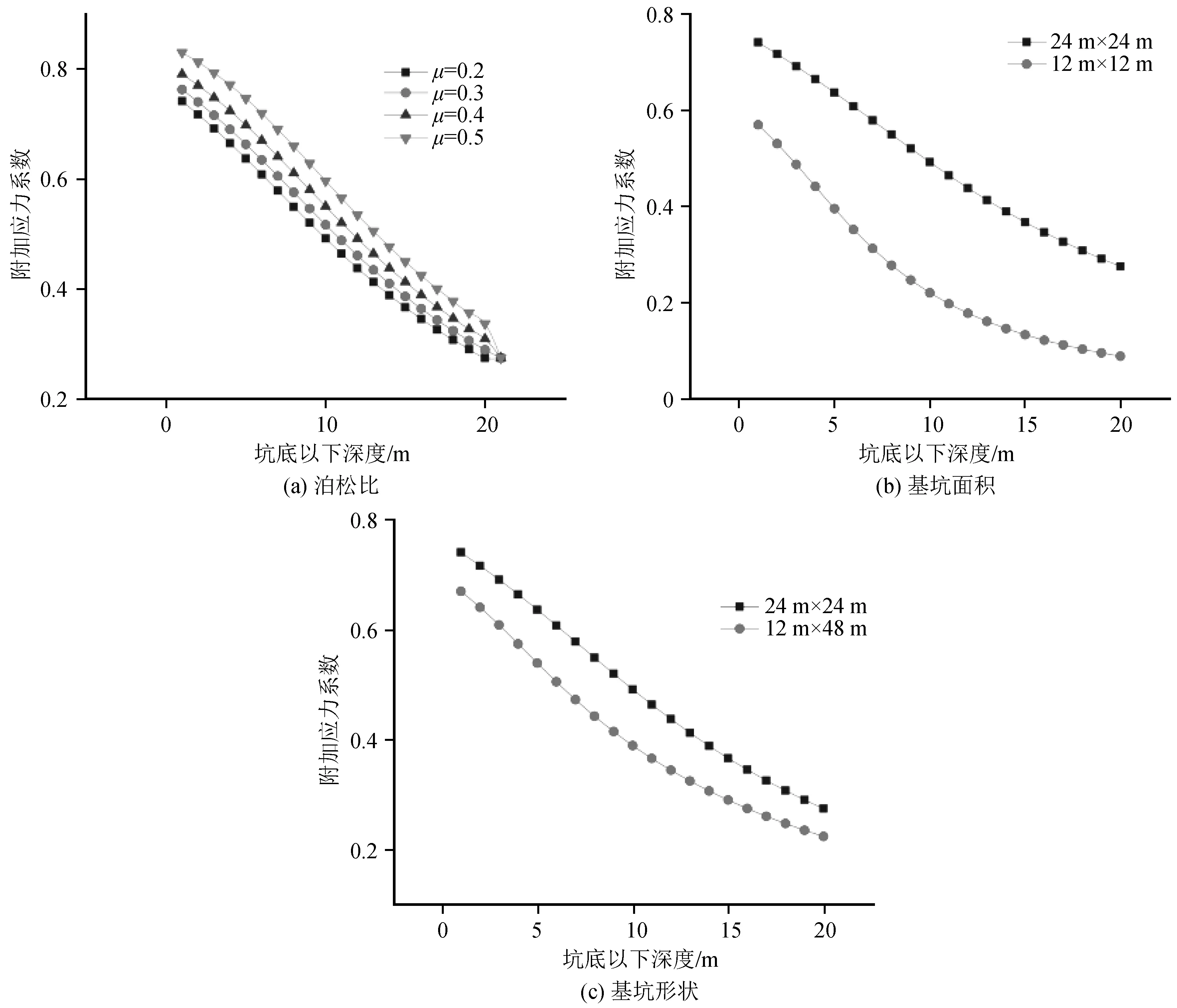
图4 卸荷附加应力系数随泊松比、基坑面积及基坑形状的变化Fig.4 Variation of unloading additional stress coefficient with Poisson's ratio, foundation pit area and the shape of foundation pit

2 开挖卸荷作用下土体的卸荷模量的计算

基坑在开挖过程中,土体的变形模量不是恒定的,而是随着应力状态的改变变形模量也发生变化,因此在基坑开挖变形的计算中,采用传统常规加压条件下土体的弹性模量来计算土体开挖作用下周围环境的变形往往是不准确的。为了准确预测基坑开挖卸荷引起的周围环境的变形,在计算过程中考虑卸荷作用下的土体变形模量的非线性变化是必不可少的。

根据已有文献的研究,土体的卸荷模量不仅取决于土体的物理性质,还与其所经历的应力路径有关。根据大量卸荷试验研究,土体在开挖卸荷应力路径作用下,其应力-应变关系可以用邓肯-张双曲线模型来描述:

(6)

式中:σ1、σ3分别为最大主应力和最小主应力;ε1为轴向应变。

其线性关系可表达为:

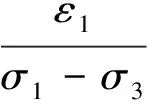
(7)

式中:a、b分别为所拟合的直线的截距和斜率。

从式(7)可知,初始切线斜率为1/a,定义为侧向卸载条件下的初始切线弹性模量Ei=1/a,而b与双曲线的最终渐近线有关。其定义为:

(8)

根据何世秀等[14]的实验研究,土体初始状态下的变形模量与其初始固结压力有关。为了消除土体初始应力状态对卸荷变形模量产生的影响,式(7)可以变形为:

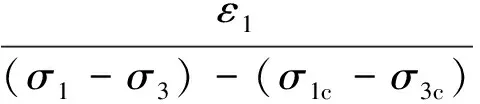
(9)

式中:σ1c、σ3c分别为土体初始固结条件下的轴向压力与围压值,且σ1c/σ3c=K0。定义破坏比Rf为:

(10)

(11)

式中:(σ1-σ3)f为试样破坏时的偏应力;(σ1c-σ3c)为初始偏应力。

将式(11)代入式(10)中可得到:

(12)

将式(12)代入式(9)则可以得到:

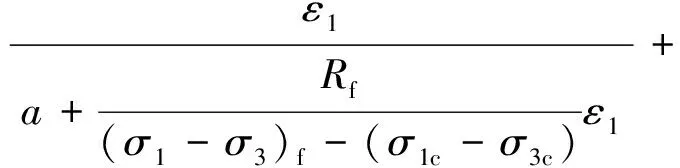
(σ1c-σ3c)

(13)

对式(13)进行求导,可以得到土体的卸荷模量,整理后可得:

(14)

为了将ε1表示成应力的函数形式,将式(9)简化可得:

(15)

将式(15)代入式(14)则:

(16)

将式(12)代入式(16)中化简可以得到:

(17)

根据基坑开挖特点,坑底土体的卸荷应力路径可以将其简化为侧向应力保持不变,轴向卸荷,因此式(17)可以写成:

(18)

根据殷德顺[15]的研究,与邓肯-张模型的推导类似,同样的,假设初始切线模量Ei随着轴向固结压力σ1而变化,且在双对数坐标上呈现直线关系,设直线的截距为k,斜率为n,则Ei的表达式写成:

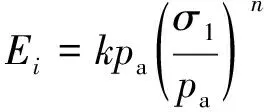
(19)

大量实验研究表明,不同应力路径下土的强度仍然符合摩尔库伦强度准则,因此在侧向卸荷时摩尔库伦强度准则仍旧适用。由莫尔圆可以得出,对压缩破坏试样有:

(20)

将式(19)、(20)代入式(18)得：

(21)

对伸长破坏的试样,根据摩尔库伦准则有:

(22)

将式(19)、(22)代入式(18)中可得:

(23)

3 分层总和法计算坑底回弹变形

采用分层总和法计算基坑开挖隆起的变形,首先要确定基坑开挖卸荷引起的坑度土体的卸荷影响深度和分层计算土层厚度和层数,然后再依次求出土体卸荷应力路径下的土体附加应力和模量,逐层求解开挖卸荷引起的回弹变形,最后求得总的坑底回弹变形值。

3.1 基坑开挖卸荷深度的确定

基坑开挖卸荷引起的坑底隆起变形的计算中,合理确定开挖卸荷作用下土体的卸荷影响深度对于准确计算基坑开挖坑底隆起变形至关重要。基坑开挖卸荷深度的确定,可以依据分层总和法中的附加应力与自重应力的比值来确定,即在卸荷开挖影响深度的计算中,可以采用卸荷附加应力与开挖所产生的总的卸荷量的比值来计算开挖卸荷的影响深度。

分层开挖卸载引起的总的附加应力计算公式为:

(24)

式中:σzij为第j层土在其上第i层土的开挖卸荷作用下所产生的附加应力;σz为第j层土在上覆n层土开挖后所产生的附加应力之和。

同理,分层开挖作用下总卸荷量的计算表达式为:

(25)

式中:pi为第i层土移除时的竖向卸荷量,可以采用式(3)得到。

若:σz/pm≤0.1,则σzj所对应的深度即为开挖卸荷作用所产生的土体最大影响深度。

基坑分层开挖的土层数n的确定,可以根据工程要求的计算精度来合理划分,在满足计算要求精度的基础上,采取合理分层厚度以减少计算量。

3.2 坑底隆起变形计算

根据上述式(5)所确定的开挖卸荷作用下土体中的附加应力以及式(21)确定的卸荷作用下的土体的回弹模量值,结合分层总和法来计算基坑开挖作用下坑底的回弹变形值。

(26)

式中:hi为基坑开挖卸荷影响范围内单层土体的厚度;Eti为式(21)推导的卸荷土体的切线模量。

4 工程实例验证分析

为了对比研究该算法的合理性,本文选取文献[4]软土基坑隆起变形的残余应力分析法中的上海地铁1号线徐家汇车站的基坑进行分析。

徐家汇地铁车站是上海地铁一号线中最大的一个车站,长600 m,宽22 m,基坑开挖深度17 m,地下连续墙厚度80 cm,设置5道支撑。其具体土体参数取值如表1所列。

表1 土层参数信息

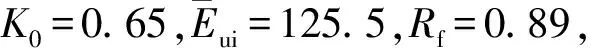
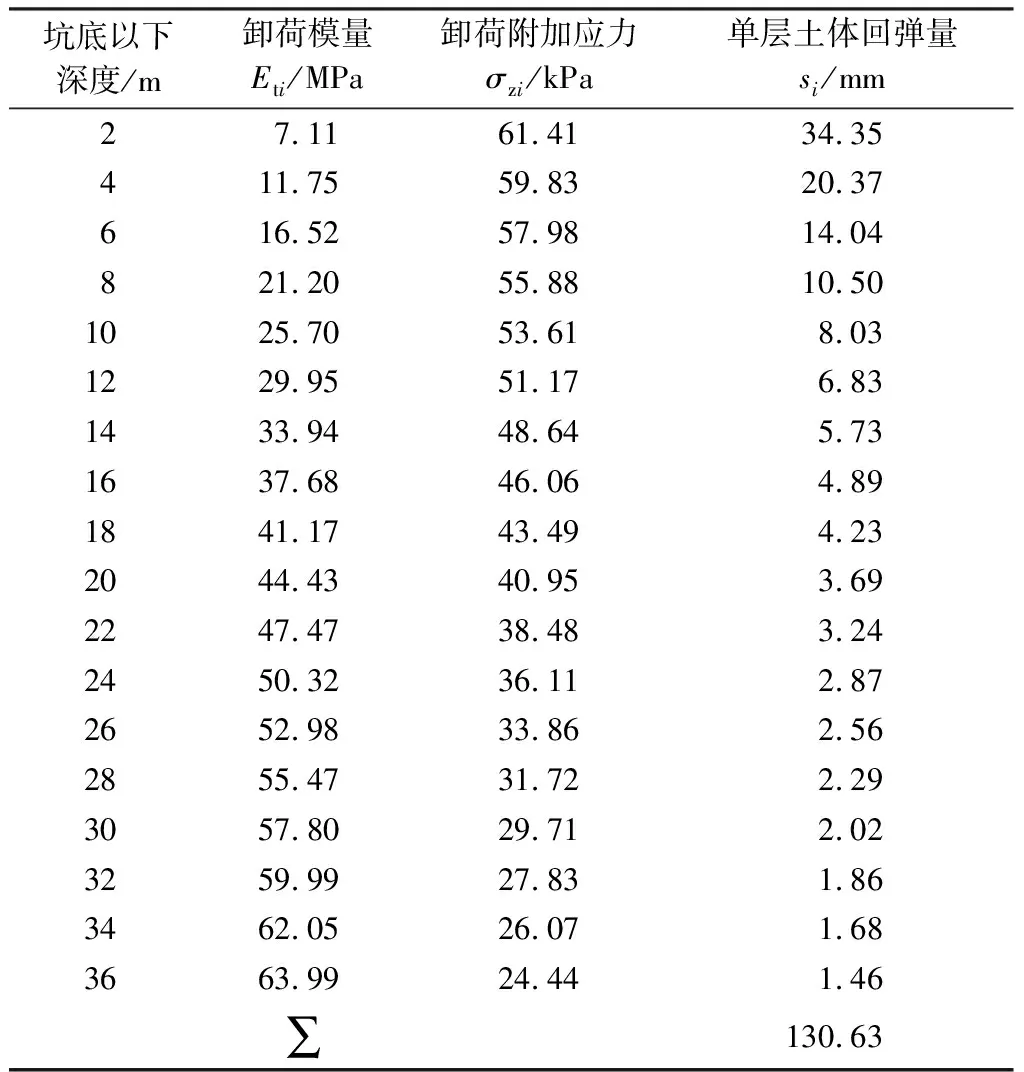
表2 坑底附加应力和变形值的计算

根据表2的结果可知,坑底最大隆起变形量为130.63 mm,该结果与文献[4]中残余应力分析方法的13.6 cm基本一致。而现场实测最大隆起变形值为12～13 cm,说明采用该方法计算基坑开挖回弹变形有较高的准确性,计算结果更加接近工程实际,可以作为预测基坑回弹变形分析的一种有效方法。同时,坑底强回弹区域为坑底以下10 m范围,约为基坑开挖深度的2/3,累计回弹变形量约为80 mm,占总回弹变形量的60%以上。

5 结语

(1) 基坑开挖引起的坑底附加应力计算中,可以采用明氏解和布氏解,矩形基坑开挖卸荷引起的附加应力计算中,采用明氏解得到的附加应力值明显小于采用布氏解,且明氏解计算的附加应力随着泊松比μ变化,即随着泊松比μ越大,卸荷附加应力系数则越大;

(2) 矩形基坑开挖卸荷附加应力系数与基坑开挖面积和基坑开挖形状也有关,基坑开挖面积越大,卸荷附加应力系数值越大,且卸荷附加应力系数沿着基坑深度方向的减小的速率也越大,正方形基坑开挖引起的附加应力系数大于长方形基坑开挖附加应力系数,但卸荷附加应力系数沿着坑底土体深度方向的变化趋势一致;

(3) 开挖卸荷应力路径中,土体卸荷模量随着轴向卸荷量的增大而减小,采用传统恒定加载应力路径下的变形模量值计算坑底回弹变形值会使得计算结果与实测值偏差较大。卸荷应力路径下,土体的应力-应变曲线满足邓肯-张双曲线模型,在基坑开挖卸荷引起的坑底土体的回弹变形的分层总和法计算中,采用基于卸荷应力路径的坑底土体卸荷变形模量更符合基坑的实际情况,计算结果更接近基坑监测值。