季冻区砂性土堤防水分场温度场及水分迁移试验研究

黄荣富, 张宝磊, 史翰超

(1. 黑龙江省生态地质调查研究总院, 黑龙江 哈尔滨 150030;2. 黑龙江省水利水电集团有限公司, 黑龙江 哈尔滨 150001;3. 机械工业第九设计研究院有限公司, 吉林 长春 130011)

0 引言

通过实地调研发现,在渗流、冻融和外部荷载等因素作用下,黑龙江干流堤防内部结构会发生较大变化,融沉、冻胀,强度弱化等一系列不利现象也随之出现,造成了直接危及堤防安全的后果。因此,研究季节性冻土区堤防基的水分场、温度场及水分迁移变化规律,对于阐述堤顶公路破坏机理具有重要意义。

黑龙江干流堤防的环境系统独特,研究黑龙江干流堤防稳定,我们主要考虑了荷载、含水量以及冻融变化等方面。目前国内外学者研究范围主要涉及冻胀和荷载变化,如Harlan[1]于1973年首次提出了土水势梯度是水分迁移的驱动力的结论;随后Fremond等[2]、Lundrdini[3]、Konard等[4]深入系统地研究了热传导、水分迁移模型和热力学性质。徐学祖等[5]于20世纪60年代对水分迁移的驱动力进行了深入研究;毛雪松[6]建立了路基非稳态温度场控制方程;原国红[7]建立了水热耦合数学模型;李杨[8]得出了非饱和冻土水热耦合控制方程。本文通过一种水分迁移的新装置,建立室内堤防物理模型,分析冻土堤防的温度场、水分场变化情况,最后利用ANSYS进行模拟分析。

1 砂性土水分迁移试验研究

1.1 砂性土物理力学性质

试样取自黑龙江干流第三标段。为保证所取试样的代表性,取堤顶以下1.5 m的土柱,用DN20PVC管完整运送回实验室。其物理力学性质列于表1,试验完全按照土工试验方法标准进行[9-11]。

表1 原状堤防砂性土物理力学性质

1.2 试验装置与试样制备

本次实验采用的是从英国引进的土体一维瞬时渗透系数测定仪(SDSWCC Measurement System),图1是改进后的试验装置结构简图。

图1 试验装置结构示意图(单位:cm)Fig.1 Structural diagram of test device (Unit:cm)

1.3 试样制备

本试验是以工程实际工况为前提,试样为重塑土,制备符合SL-1999《土工试验规程》等相关规范的系列规定。

1.4 冻融循环下水热力三场的变化规律

影响季节性砂性土堤防破坏的因素有很多,本文主要从水分补给、温度梯度变化两个方面展开研究。试验采用上一节介绍的水分迁移装置,其主要特点是试验土柱最高可达140 cm,本次试验设置高度115 cm,冻融循环次数为6次,完全可以模拟工程的实际情况。使用一维瞬时剖面法测量非饱和土对应不同冻融循环次数下的温度、含水率和应力变化。自由设置记录间隔,自动采集同一水平面数据读数[12-13]。

图2是1次冻融循环后土柱温度场随时间的变化曲线。

图2 温度场变化曲线Fig.2 Change curve of temperature field

(1) 温度场变化

图3是土柱不同深度的日温度变化曲线,从图中可以看出,土柱冻结深度在1.12 m,在冻结和融化时温度沿深度变化具有明显的滞后现象,且在温度传递的过程中伴有热量交换导致温度传递过程中损失。

图3 土柱日温度变化曲线Fig.3 Daily temperature variation curve of soil column

(2) 水分场变化

图4是一次冻融循环体积含水率随时间的变化曲线。从图中可看出:含水率与温度成正比例关系,且具有明显的滞后现象,以温度和含水率都稳定为标准,含水率滞后大约1～2天的时间,这也证实了在实际堤防中,即使温度开始回升,堤防也会继续发生鼓包、开裂的现象。

图4 水分场变化曲线Fig.4 Change curve of moisture field

2 砂性土堤防水热数学模型

2.1 温度场数学模型

受季节性冻土地区的环境温度影响。堤基土经历着融化-冻结-融化的周期性变化过程,因此堤基也必然存在着温度重分布的变化过程,根据连续运动方程和热力学定律,平面稳态热分析控制方程[14-15]:

(1)

式中:T为冻土的瞬时温度(℃);t为运行时间(s);ρ为冻土密度(kg· m-3);L为冻土中冰水相变潜热(J·kg-1);c为土体比热[J/(kg·℃)];λ为冻土的导热系数[W/(m·K)];ρi为冻土中冰密度(kg·m-3);θi为冻土含冰量(%)。

转换为瞬态热分析矩阵形式为:

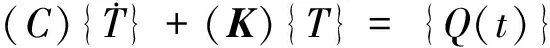
(2)

2.2 水分场数学模型

土冻融过程中根据温度梯度和相变的变化规律,将冻土含水率分为含冰量和含水量考虑。根据质量守恒定律、多孔介质理论和达西定律结合得出水分运动的基本方程[16]:

(3)

式中:θw为冻土中未冻水含量(%);θi为冻土总含水量(%);ρi为水的密度(kg·cm-3);D(θ)为非饱和土水的扩散率其值等于导水率K(θ)和比水容量C(θ)的比值[17]。

水热联系方程:

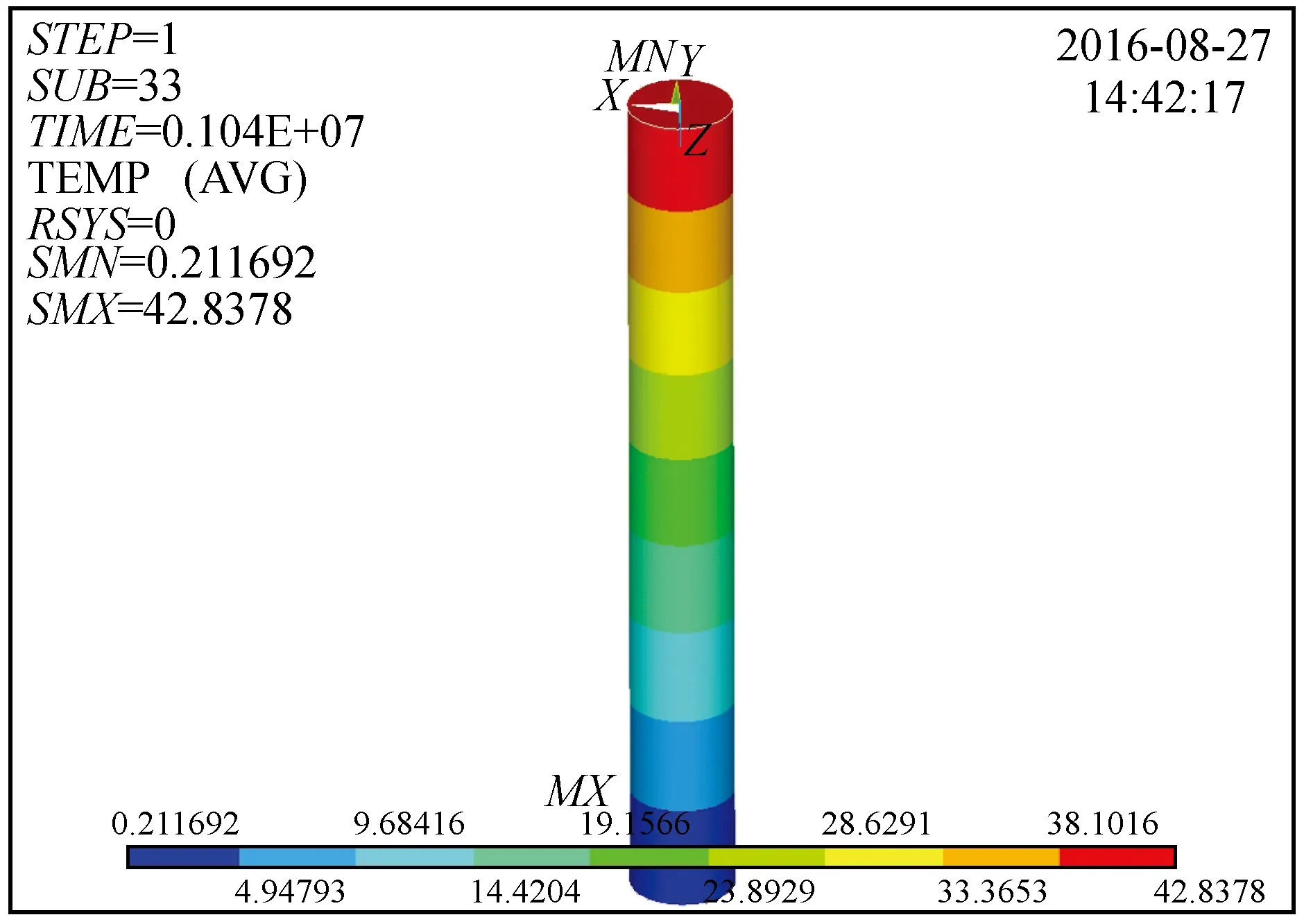
θw=f(T)T

式中:T和Tm是堤防基础温度和冻结温度。

3 ANSYS有限元模拟分析

由于温度变化引起土中一系列参数变化,因此,在ANSYS分析中运用热-应力耦合分析,首先进行瞬态热分析得出系统随时间变化的温度场及其他参数,随后将其作为热荷载进行应力分析,计算时间共计288 h,时间步长1 h。主要参数在第2节均已给出。

分析步骤:定义单元类型及材料属性-建模-生成有限元模型-施加温度荷载-求解-转换求解类型-施加节点温度荷载-压力荷载-边界约束-求解,计算结果如下图所示。

图5为三维实体模型,图中不同颜色代表稳定温度场等温线分布图,由图可知,该系统单项传热稳定时间是12 d,最大冻结深度为111 cm,从整个温度场分布来看其主要相变取发生在地表到地下1 m左右,与实测冻结深度相同。

图5 温度场等温线分布图Fig.5 Isotherm distribution of temperature field

图6为总体温度梯度分布图,从图中可知,待温度场稳定后,顶部最大温度梯度为42.84 ℃,最小温度梯度为0.21 ℃。同时温度梯度从堤顶向下逐渐衰减,到最大冻结深度温度梯度逐渐减小到0。

图6 温度梯度分布图Fig.6 Temperature gradient distribution

图7为热应力耦合后得到的应力分布图,从图中可知应力分布主要受顶部荷载的影响,且顶部出现不均匀沉降,下沉量为5 cm,应力主要集中在上部10 cm内。

图7 应力分布图Fig.7 Stress distribution

4 结论

(1) 堤顶公路破坏主要是由堤身基础冻胀引起的。其首要原因是温度变化导致其含水量分布不均,在堤身内部形成冻胀,产生不均匀沉降,致使堤顶公路受力不均发生破坏。

(2) 黑龙江干流砂性土堤防冻结深度平均1.12 m,且主要相变区在顶部向下1 m深度内变化,最大温度梯度为42.84 ℃,最小0.2 ℃。含水率随温度梯度有明显的滞后现象,冻结稳定后土层内残余含水量为5%。

(3) 给出的数学模型能较好地模拟三场的变化,在软件计算中精度较高,且与实测数据对比误差较小。水分迁移装置室内测试温度变化、含水量变化和应力变化都能较好地模拟室外情况。