基于深度学习的配电网智能检修模型及其求解方法*
程韧俐,吴 新
(深圳供电局有限公司,广东 深圳 518000)
随着风、光等可再生能源不断并入配电网,配电网中的设备、线路规模日益增大,可再生能源发电的随机性、时变性使配电网发生故障的概率变大,引起了国内外专家学者的高度重视[1-2]。
不断增大的配电网规模、高要求的供电可靠性对制定高效、合理的配电网检修方法提出了严峻挑战。对此,国内外专家学者纷纷投入这一研究之中,提出了许多卓有成效的方法,总体上可以分为3 类,第1 类从停电损失、检修费用等经济的角度建立可靠安全的检修模型,第2 类从安全可靠的角度建立停电负荷损失最小的检修模型。
第1 类研究主要从经济的角度建立优化模型,如黄弦超[3]、张粒子[4]、郭建[5]等分别以检修成本、停电损失最小及其之和为优化目标,采用遗传模拟退火、多目标粒子群优化方法进行求解。此类研究实质上侧重经济性,而弱化了检修的可靠性。
第2 类研究主要从可靠性的角度建立负荷转移优化模型,如黄弦超等[6]建立了负荷转移路径和设备检修时间的联合优化模型,期望反复优化得到售电损失最小、停电负荷最小、网损最小的负荷转移方案。黄弦超等[7]以负荷转移方案为目标,加入分布式发电运行方式路径转移优化约束,建立了以分布式电量费用最小、售电损失最小、开关操作费用最小等优化目标,采用遗传算法和启发式算法联合求解该目标的方法。熊小伏[8]、夏莹[9]等从气象因素角度出发,以可靠性指标损失最小为优化目标,建立了不同气象条件下设备故障率、修复时间综合模型,采用遗传算法求解最佳维修计划。黄喜健等[10]从系统的角度,以预算成本和人力资源为约束条件的系统平均停电频率、平均停电时间、失电量的变化量最大为目标的检修模型,采用规格化法向约束方法求解该模型。此类研究的本质是侧重可靠性和安全性,相对降低了经济性。
第3 类研究是在上述2 类研究的基础上提出的,力求解决经济性和可靠性2 方面目标,如许旭锋等[11]建立了上层检修计划表、检修资源安排方案模型,下层为转移或恢复负荷过程的系统状态量和开关状态函数,通过粒子群算法和启发式负荷转移方法分别交叉求解。张静怡等[12]为了提高配电网供电可靠性和经济性,以检修时间、检修方式、检修过程中故障风险最小为目标,建立综合考虑电网安全和检修关系的多目标优化模型。刘志文等[13]建立了上层检修总费用最低为目标、下层停电负荷最小为目标的双层反复迭代求解模型。实际上,此类研究仍以经济性或可靠性某一方面为主目标,另一方面配合优化为子问题,本质上与第1 类、第2 类相同。
对此,以帕累托纳什(Parato-Nash)原理为基础,提出了以可靠性和经济性为目标的帕累托纳什均衡双赢多目标优化模型。其中,可靠性以停电持续时间和停电负荷量作为优化目标,经济性以停电失负荷费用、检修费用、负荷转移网损费用和开关数量操作次数费用为目标。
最近,大数据技术应用在电力系统安全监测、经济调度等领域得到广泛关注[14-16],但尚未看到有关应用人工智能方法求解配电网检修模型的报道出现。因此,采用人工智能中的深度学习方法求解建立的可靠性、经济性帕累托纳什均衡双赢模型。
1 配电网检修经济性模型
配电网检修的核心是在检修时间内使检修总费用最低,包括检修费用、负荷转移网损费用、失负荷费用、开关操作次数费用最低:

式中:f1表示检修费用;f2表示负荷转移网损费用;f3表示失负荷费用;f4表示开关操作次数费用;N表示配电网中检修设备总数;T表示检修时段数量;αij表示设备i在时段j的检修状态;Cij表示设备i在时段j的检修成本;βj表示在时段j的停电成本;Pl表示网损;γj表示时段j的负荷成本;Pj表示时段j的失负荷数量;M表示开关总数;ηij表示时段i开关j的开关操作成本;Kij表示时段i开关j的开关操作次数。
式(1)在优化过程中,还需要一些约束条件,如设备同时检修约束:

式中:Hi表示时段i内同时检修的设备数量;W表示允许同时检修的设备总数。
设备不允许同时检修约束:

式中:Ai和Bi分别表示在时段i内同时的检修设备。
开关操作次数约束:

式中:Kij表示在时段i内开关j操作次数;Ωi表示在时段i内允许的操作次数。
失负荷数量约束:

式中:Pi表示在时段i内失负荷量,Pmiax为其允许的失负荷量上限。
检修时间连续约束:

式中:ti+1-ti表示时段i+1 与时段i的时间间隔;ε表示一个近似0 的数。
2 配电网检修可靠性模型
配电网检修的核心目标是可靠性,降低配电网运行风险,即合理合适的检修计划能够降低停电时间和失负荷量,因此检修过程中的高可靠性就是使停电时间、失负荷量最小:

式中:f5表示失负荷数量;f6表示停电时间;T表示时段总数;H表示设备总数;μij表示时段i内设备j的故障率;κij表示时段i内设备j的修复时间;N表示负荷点总数量;Pijk表示时段i内负荷点k的有功功率;Dij表示时段i内设备j对应的用户数量。
对应于式(2)的优化目标,也存在一定的约束条件,如潮流约束:
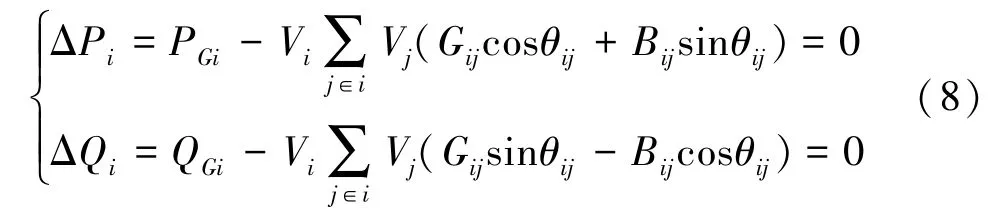
式中:PGi表示节点i注入的有功功率;QGi表示节点i注入的无功功率;Vi表示节点i的电压幅值;Gij表示节点i与j之间的电导;Bij表示节点i与j之间的电纳;θij表示节点i与j之间的相位差。
节点i电压幅值Vi上下限约束:

配电网输电线路l有功功率Pl、无功功率Ql约束:

3 帕累托纳什均衡优化原理
Pareto-Nash 均衡优化原理主要用于多目标优化问题,通过多目标之间的协调,达到多目标均衡最优,用数学模型描述为[17-19]:

式中:fi为第i个目标函数;Xi为第i个变量;gi、hi分别为不等式和等式约束;和分别表示变量的下限、上限。
通过求解式(11),可以得到Parato 最优解。
对于本文第1 部分和第2 部分的目标优化模型,其目标函数主要是经济性和可靠性2 个方面,等式约束和不等式约束详见式(2)~式(6)、式(8)~式(10)。
在Nash 博弈中[20],获得Parato 最优解后还需要从该解中选择一个最优折中解作为最终决策,因此利用基于Nash 均衡点的多目标决策模型对最优折中解进行求解,以获得最佳的经济性和可靠性,其数学模型描述如下:

式中:Hi表示Parato 第i个目标的最优解;hij表示第j个Parato 最优解对应于第i个目标的均衡值,fij为其归一化值;Mobj为目标个数;ξi表示第i个目标的重要程度;υi表示第i个目标值的上限。
式(12)是一个典型的多目标带约束的非线性规划问题,传统主要由粒子群算法、二次规划法等求解,存在陷入局部最优、无法收敛等问题[21]。
对此,在配电网时间、空间都具备同步快速采集设备的基础上,可以利用大数据分析技术及其人工智能技术解决上述问题。
4 深度学习的求解方法
4.1 深度学习方法
人工智能是具有建模、扩展、改善人类行为的一门前沿技术,其目标是利用机器实现人类认知、分类、识别、决策等功能[22]。
深度学习是人工智能中的一种,其本质是含有多层隐含网络及其权值作为反馈修正功能的多输入神经网络,其中的长短期记忆网络(Long Short Term Memory,LSTM)基本结构如图1 所示[23-24]。
图1 所示LSTM 的运行方式为:首先,LSTM 每一个单元通过最左侧的遗忘门接收t时刻输入信息xt及其t-1 时刻LSTM 的隐含信息ht-1,在多个激活函数σ的作用下对输入信息进行过滤,从而获得遗忘门的输出ft,该数值确定长期记忆Ct的历史比例:

图1 深度学习LSTM 内部结构图

式中:wfx、wfh、wix、wih、wcx、wch、wox、woh、wy表示权值系数;bf、bi、bc、bo、by为偏置量。
上述式(13)确定历史输入信息,与此同时,输入门还要决定让部分新信息加入到LSTM 中,包含过滤当前输入信息xt、LSTMt-1 时刻隐含信息ht-1的it以及新内容:

通过式(14)~(15)的过滤信息、增加新信息,可以得到t时刻LSTM 的记忆信息Ct:
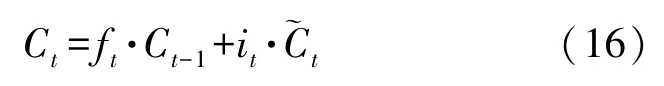
根据t时刻LSTM 的记忆信息Ct,进一步由输出门确定输出到当前状态ht的比例ot和当前状态信息ht:

经过式(18)计算,可以获得输出门当前状态信息ht,最后得到LSTM 网络的输出值:
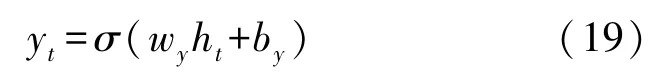
LSTM 中的式(13)~式(19)激活函数σ一般选择sigmoid 函数,通过将变量映射到[0,1]之间以过滤部分信息;bf,bi,bc,bo,by为偏置量。
实际中一般采用多个LSTM 单元,每个LSTM 单元中的输入、输出都可以是多维数据矩阵,从而实现从历史数据中多维度、多神经元、多权值学习,流程为:
(1)从数据库中选择多维历史数据信息,建立多维输入数据向量和对应的多维输出向量,作为历史训练集。
(2)将历史训练集中的输入数据输入到LSTM中,得到预测值。
(3)根据预测值与真实值的误差利用反向传播算法对LSTM 权值,即式(13)~式(15)、式(17)进行学习训练。
(4)训练好的LSTM 权值作为未来的计算,输入数据即可以得到输出值,即得到LSTM 网络的输出值yt。
4.2 深度学习LSTM 求解方法
在配电网长期运行过程中,输电线路、电力变压器、断路器等设备会受到电、热、机械等效应作用,从而产生老化、绝缘损坏等状态,由此产生的配电网运行状态、故障情况等都记录在配电网正常巡检、带电检测、在线试验、环境温度、电网运行状况等过程中,由此可形成式(1)、式(7)目标函数中的自变量,并可以按照传统方法求解出因变量及式(12)中因变量状态空间,从而形成自变量、因变量历史大数据。
将式(1)、式(7)、式(12)形成的自变量、因变量代入式(13)~式(19)中,利用LSTM 的反馈学习修正神经元,可以获得最优收敛数值。
5 算例仿真
以IEEE-RBTS BUS5 配电网系统为例,验证上述算法的正确性,该系统接线图如图2 所示。
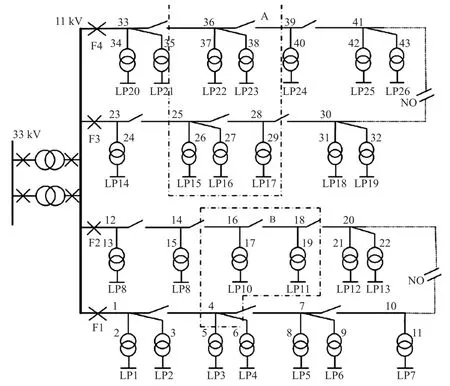
图2 IEEE-RBTS BUS5 接线图
在图2 的配电网中,保护输电线路、变压器的断路器、隔离开关的正常动作率为100%,隔离开关的动作时间为1 h,协调输电线路的正常检修时间为5 h,非正常时间为10 h。
图2 所示配电网电压等级为11 kV,包含26 条馈线,包含常开支路和常闭支路,各馈线的最大容量为5 000 kW,节点电压标幺值上下限为Vmin=0.95,Vmax=1.05。设输电线路7、14、17、28、30、37 需要在15 h 内完成检修,检修时间为2 h,在检修期间内的负荷、电价、检修费用的变化曲线如图3 所示。

图3 配电网负荷、检修费用和电价曲线
经过所提出的深度学习的帕累托纳什均衡算法计算,经济性目标迭代了15 次,可靠性目标迭代了18次,二者得到均衡最优,最优检修结果如表1 所示。
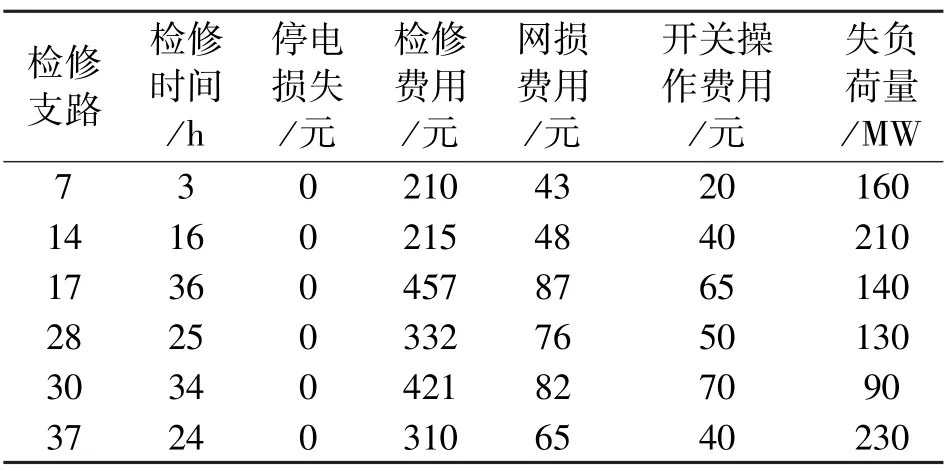
表1 经济性、可靠性检修优化结果
由表1 可见,所有待检修线路的停电负荷全部转移到其他馈线,表明该方法从理论上解决了实际问题。除此之外,与文献[10-12]经济性相比,结果如表2 所示。
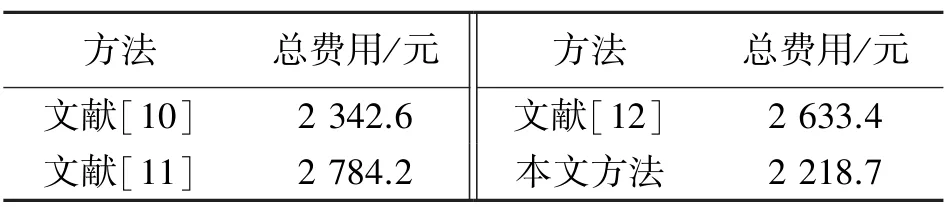
表2 经济性比较结果
由表2 可见,该方法经济性较低,主要原因是考虑了设备检修过程中保证可靠性前提下,在不同时段进行检修,最大化保证可靠性,同时考虑最优负荷转移切换。
6 结论
针对配电网检修过程中的经济性、可靠性问题,基于经济学原理中的帕累托纳什均衡原理,建立了配电网检修经济性、可靠性模型,采用深度学习理论进行求解。通过IEEE-RBTS BUS5 系统进行验证,表明了所提方法的有效性。

