多纤维捕集过程中细颗粒湍流团聚模拟研究

张俪安,刁永发,楚明浩,贾中坚,沈恒根,孙 静

多纤维捕集过程中细颗粒湍流团聚模拟研究

张俪安1,刁永发1*,楚明浩1,贾中坚1,沈恒根1,孙 静2

(1.东华大学环境科学与工程学院,上海 201620；2.甘肃兰菲环保科技有限公司,兰州 730030)

基于随机多层纤维过滤介质算法建立了平板式三维拟态化结构.利用计算流体力学-颗粒群平衡模型(CFD-PBM)对多纤维捕集过程中细颗粒湍流团聚进行数值模拟研究,并采用分区法求解颗粒群平衡方程(PBE).通过控制变量法分析表明:多纤维捕集过程中存在着明显的颗粒团聚行为.粉尘颗粒的团聚程度随停留时间增加而增强,当³/(速度方向模型尺寸长度/入口风速),团聚逐渐趋于稳定;当max·£,入口风速越大,颗粒团聚程度和团聚速率越大,最终的团聚程度取决于入口风速和停留时间;颗粒粒径越大,粉尘颗粒的团聚程度和团聚速率越小.出口颗粒平均粒径与初始粒径相比增长倍数越小.粉尘颗粒体积分数越大,颗粒团聚程度以及团聚速率越大.当= 0.1m/s,p= 1.0μm,VF > 0.003636, Bin-7～Bin-0区间数量浓度对数分布呈线性比例关系.

计算流体力学-颗粒群平衡模型；颗粒群平衡方程；分区法；湍流团聚；多纤维

颗粒物通过呼吸道进入肺部会产生沉积和滞留.粒径在2.5μm以下以及2.5～5.0μm的颗粒物能够进入肺泡,进而干扰肺部的气体交换,损伤肺泡和粘膜,引起肺组织的慢性纤维化等一系列病变,甚至会影响人体免疫功能,呼吸和中枢神经系统[1].目前最常见的去除工业废气中颗粒物的方法是依靠纤维滤料捕集技术.

早期对于多纤维捕集粉尘颗粒的研究主要分为两类,一类集中体现在多纤维建模[2-3],其方法是首先利用SEM、MRI以及X射线断层摄影等技术获得纤维随机分布的微观结构,利用Matlab进行编码生成脚本文件Txt,导入到建模软件生成多纤维过滤介质结构模型,其中,典型的多纤维过滤介质包括平板纤维过滤介质[4-5]、V型褶式纤维过滤介质[6]以及U型纤维过滤介质[7].另一类则体现在多纤维捕集颗粒数值模拟计算方法上.目前基于离散相模型进行数值模拟能方便计算出多纤维捕集效率[8-9]以及颗粒在流场中的运动轨迹[1,10],但是该方法忽略了流场中颗粒对颗粒的相互作用.与此同时,能够计算流场中颗粒与颗粒相互作用的离散单元法多用来研究粉尘颗粒在纤维表面的团聚沉积[4-5],并且计算时Fluent和EDEM两软件之间需要双向耦合,使得该方法计算使用时存在周期时间长的弊端.而基于CFD-PBM方法在计算颗粒之间相互作用的同时不需要考虑双向耦合的问题,因此可以很好的计算出颗粒与颗粒之间的团聚行为[11-13].

通过计算多纤维捕集结构中流体雷诺数Re<1,属于层流运动,运用-湍流模型以及湍流团聚核的合理性假设包括:(1)从宏观角度,袋式除尘内部是复杂的三维湍流流场[14],那么粉尘颗粒在被纤维捕集过程中必然经历着碰撞和湍流团聚行为.同时,根据研究表明[4],工况的改变可能导致纤维捕集过程湍流的变化;(2)若采用层流计算,默认颗粒在流场中不发生碰撞,与实际有一定误差;(3)使用层流和-湍流模型时,多维捕集结构内部的速度分布相同.

为获得纤维捕集过程中更为符合物理真实的气固两相流流动特性,基于CFD-PBM方法对多纤维捕集颗粒过程中流场内颗粒微观变化团聚现象进行系统的研究.同时,颗粒团聚后的破碎问题根据文献[15]研究结果可忽略.在传统欧拉双流体模型的基础上加载群体颗粒模型,综合考虑了停留时间、入口风速、粉尘粒径、以及体积分数对粉尘颗粒湍流团聚的影响.为后续研究纤维捕集过程中的团聚奠定了一定的基础.

1 数值计算模型

1.1 多相流模型

多相流模型采用欧拉-欧拉双流体模型,连续性方程和动量方程如下[5]:

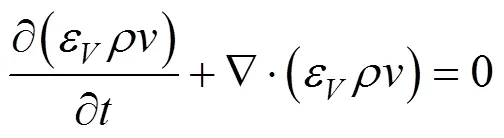
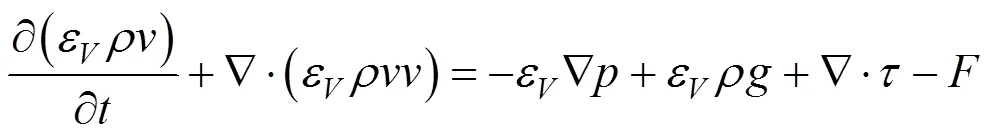
1.2 颗粒群平衡方程

颗粒团聚可以用粒子的聚并动力学方程(General Dynamic Equation,GDE/PBE)来进行描述,即聚并动力学方程如下[16]:

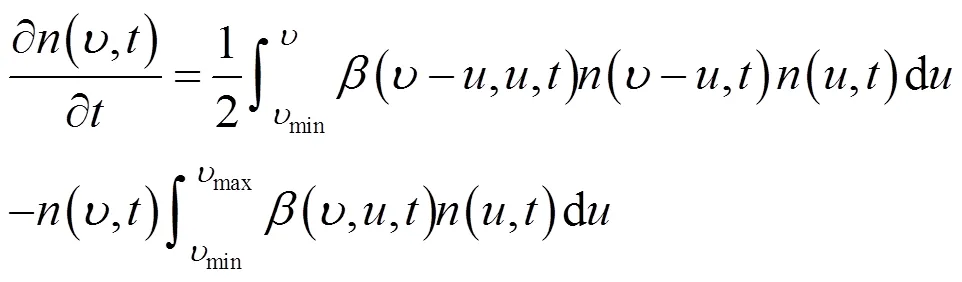
1.3 湍流聚并核函数

通过计算可知K的数值趋于0,根据Saffman和Turner所提出的零惯性颗粒湍流模型来进行描述,颗粒湍流聚并核函数为[17]:

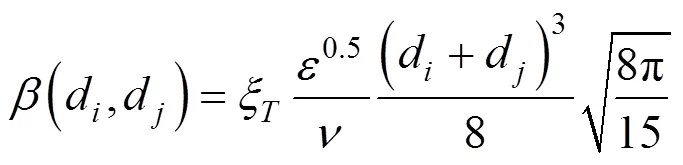
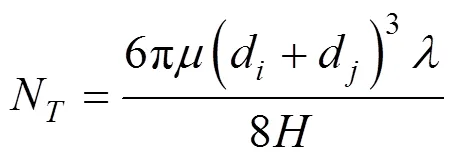
式中:V表示颗粒之间实际发生的碰撞次数与理论上发生碰撞的比例,即聚并系数;N为粘性力与范德华力的比值;为颗粒变形率;表示湍流耗散率, m2/s3;为气体的动力黏度,Pa·s;为气体的运动黏度,m2/s;d和d表示两颗粒的直径,μm;为Hamaker常数.

2 边界条件

2.1 多纤维建模

为建立纤维随机分布,基于Poisson(泊松)随机直线过程[18-19],生成过滤介质三维随机模型的控制算法.直线L用直线到原点的距离X和方向角M描述,随机X可以是任意实数,随机方向角M在[0, π]之间取值.采用Poisson随机过程对相互独立的随机序列(1,1), (2,2),…,(X,M)进行描述,由直线簇L中所有相互交叉的直线(1,1),(2,2),… ,(X,M)构成多纤维结构.对于多纤维的建模引用文献[20]的方法,模型如图1所示:

图1 多纤维过滤介质结构模型

2.2 多纤维捕集模型建立

对颗粒群平衡方程(PBE)采用分区算法,初始颗粒分布为单分散相体系,以入口粉尘粒径为1.0μm为例,Ratio Exponent数值取1.0,根据Gelbard[22]提出的分区方法,将颗粒群大小划分为8个子区间,如表1所示.

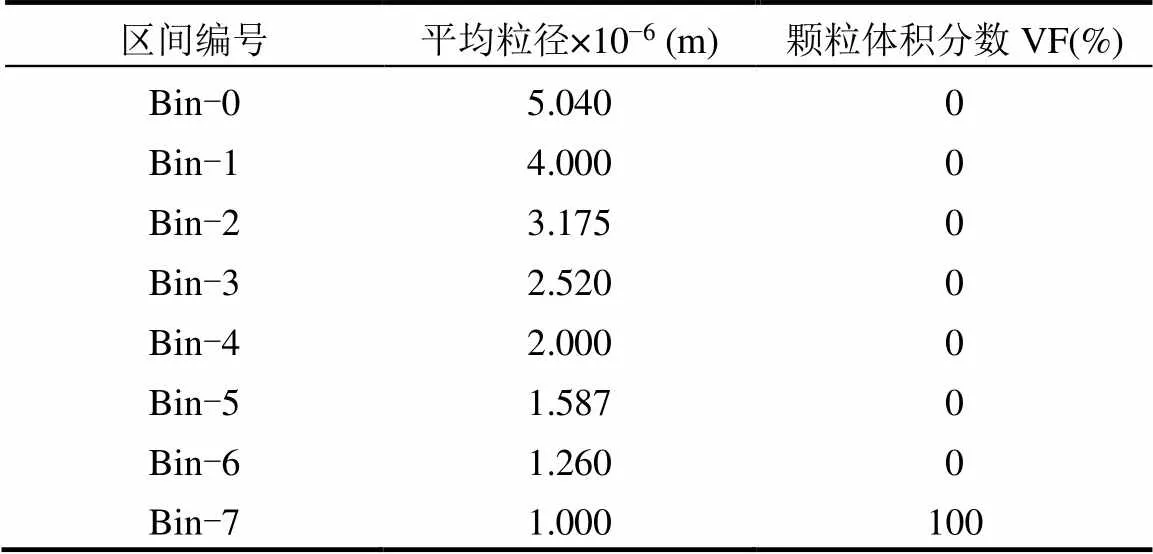
表1 Bin-7～Bin-0区间粒径大小以及区间颗粒初始占比

Bin-7～Bin-0区间粒径大小由初始粒径计算得来,(分区后,相邻区间后一区间颗粒体积与前一区间颗粒体积满足V+1=fV,比例系数1.08£f£3.0).不同初始粒径对应不同组的Bin-7～Bin-0.通过计算, 0.5～5.0μm对应的Bin-7～Bin-0如表2所示.团聚过程为Bin-7→Bin-6→Bin-5→Bin-4→Bin-3→Bin-2→Bin-1→Bin-0.在每个子区间内对群体平衡模型进行积分即可得到一系列离散的方程.同时,使用EWF模型结合计算粉尘颗粒在纤维表面的沉积.

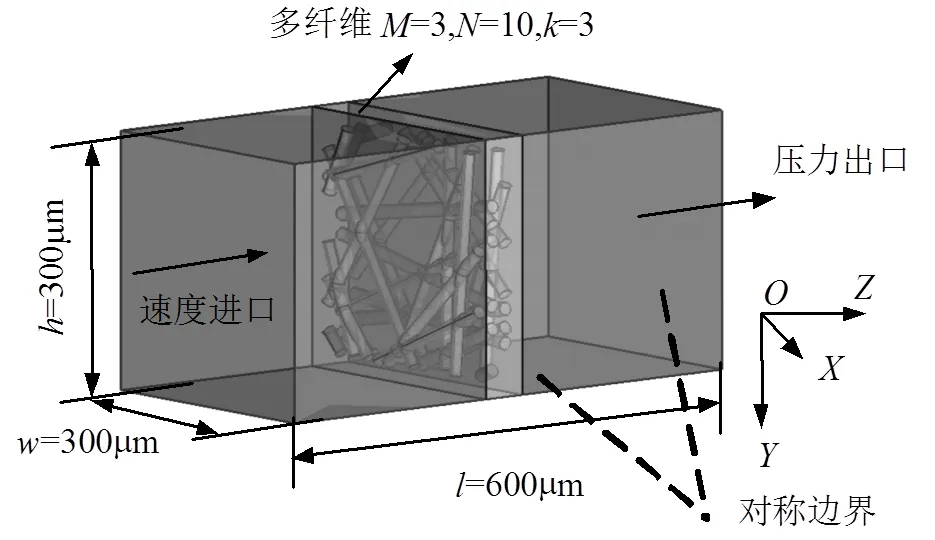
图2 计算区域及边界条件示意

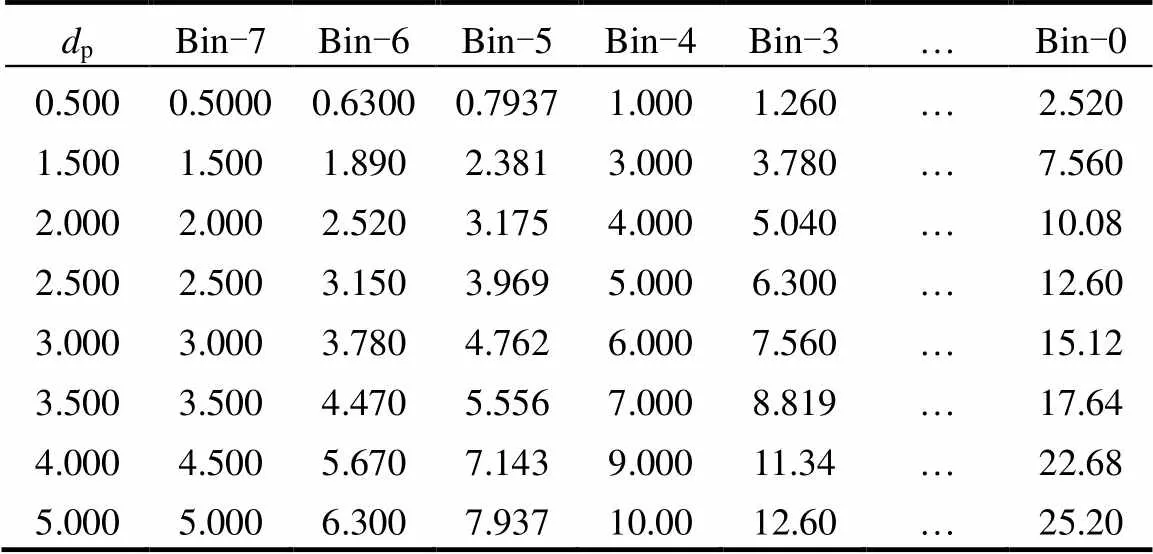
表2 不同初始粒径下Bin-7～Bin-0区间对应的粒径值

3 正确性验证

3.1 网格独立性检验

为排除多纤维网格数量对数值模拟的影响,对其进行了网格独立性检验(=3,=10,=3μm),计算不同网格密度下的压力损失,结果见表3,当网格数量由Mesh1增长到Mesh2时,压降的变化为4.009 %,网格数量由Mesh2增长到Mesh4时,压降的变化为0.5694 %,即多纤维捕集结构网格达到270万左右时,进出口的压降基本保持不变,因此选择270万的网格进行数值模拟计算,计算所使用的网格为四面体非结构化网格,在划分网格时将固体域纤维体定义为Solid,流体域定义为Fluid.

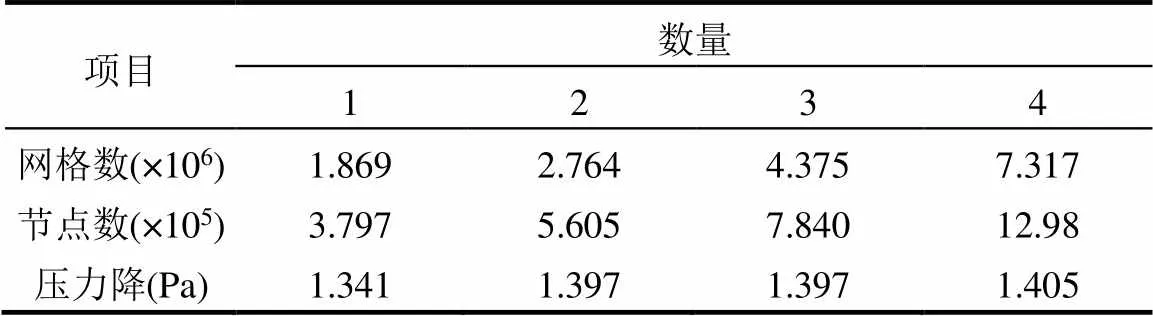
表3 网格独立性检验(v=0.1m/s)

3.2 模型验证

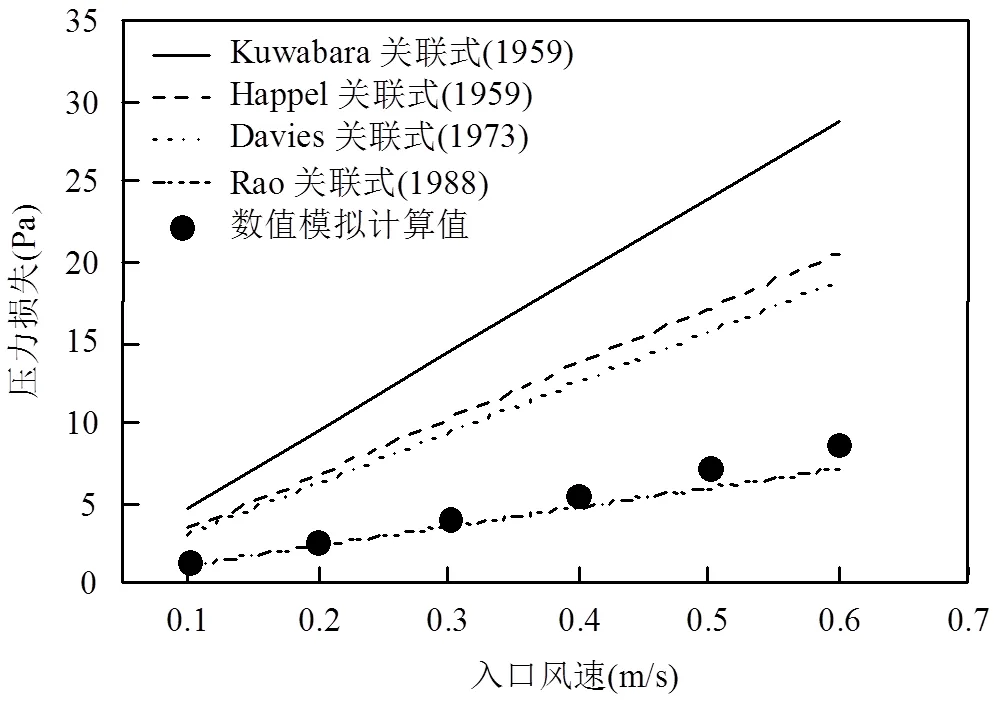
图3 多纤维过滤压降数值模拟与经验公式对比

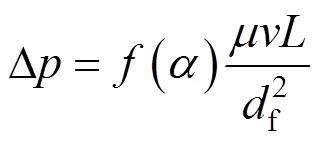
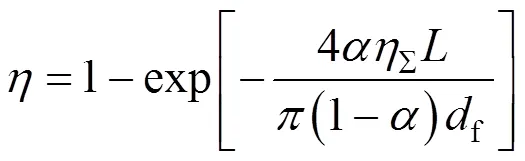
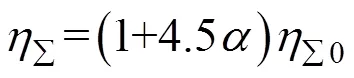
同时,将多纤维过滤效率与经验公式(6)进行对比[1,8-10],由于所研究的粒径范围为0.5～5.0μm,常温[27]下当p=0.5μm时,粉尘颗粒的布朗团聚可以忽略.由图4可知,多纤维对粉尘颗粒进行捕集时,数值计算所得到的趋势与经验公式理论模型基本一致,基于CFD-PBM计算符合数值模拟计算的要求.

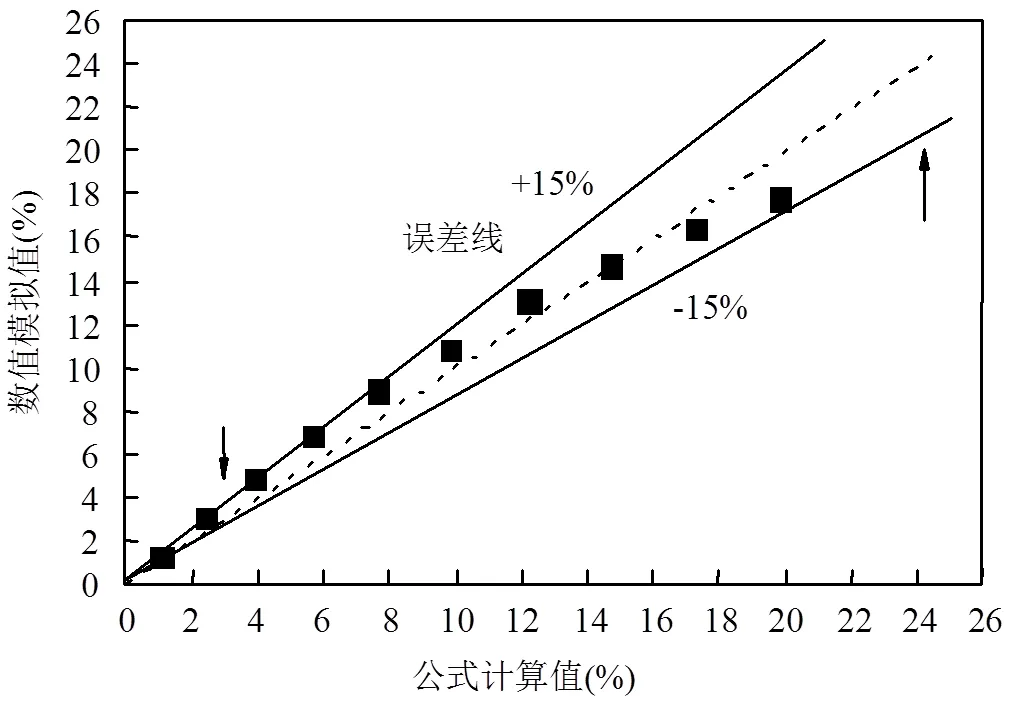
图4 多纤维过滤效率数值模拟与经验公式对比

4 数值计算结果

4.1 捕集过程中停留时间对颗粒湍流团聚的影响

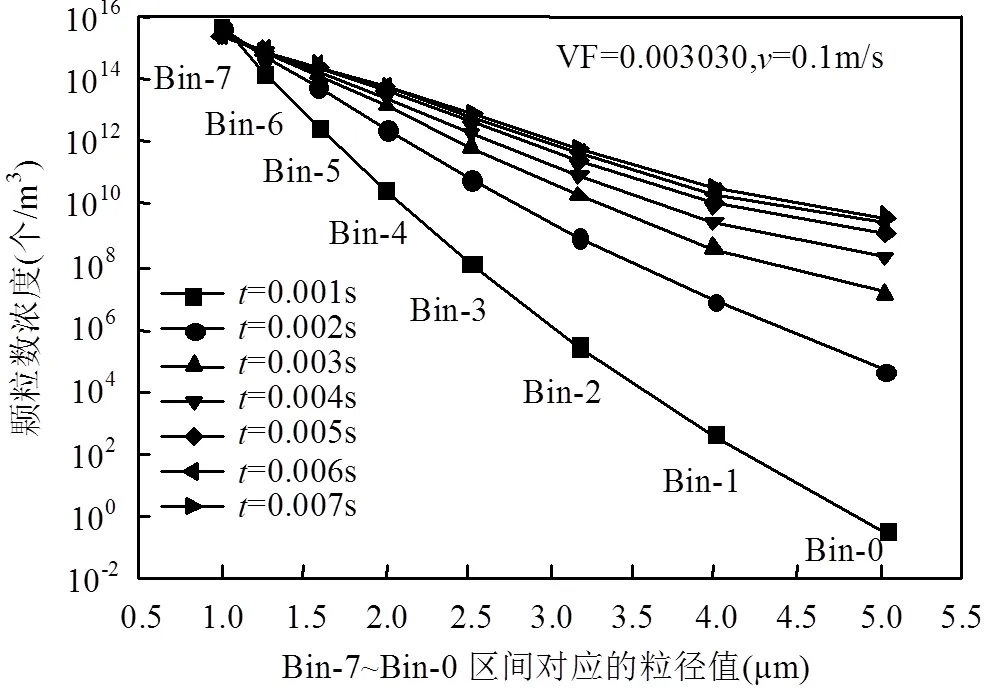
图5 停留时间对颗粒湍流团聚的影响

由图5可知,Bin-7区间颗粒数量浓度减小,Bin- 6～Bin-0区间颗粒数量浓度增加,说明颗粒在多纤维捕集模型中存在明显的碰撞与团聚,随着时间的增加,粉尘颗粒的湍流团聚效果逐渐增强,粉尘颗粒在流场的作用下碰撞后受范德华力发生团聚,粒径逐渐向大颗粒偏移.当³/,团聚逐渐趋于稳定.粒径段越靠近初始颗粒,达到稳定所需要的时间越短,小粒径段颗粒相比较于大粒径段颗粒团聚速率较大.但单位时间内小粒径段颗粒数量浓度变化百分比较小.

4.2 捕集过程中入口风速对颗粒湍流团聚的影响

由图6可知,团聚呈现出不同的三段规律,Ⅰ段(Bin-7区间),入口风速越大,稳定后Bin-7区间颗粒数量浓度越大,表现出入口风速越大,颗粒团聚程度越小;Ⅱ段(Bin-6～Bin-2区间),入口风速越大,稳定后Bin-6～Bin-2区间颗粒数量浓度越小,表现出入口风速越大,颗粒团聚程度越小;Ⅲ段(Bin-1～Bin-0区间),入口风速越大,稳定后Bin-1～Bin-0区间的数量越大,表现出入口风速越大,颗粒团聚程度越大.

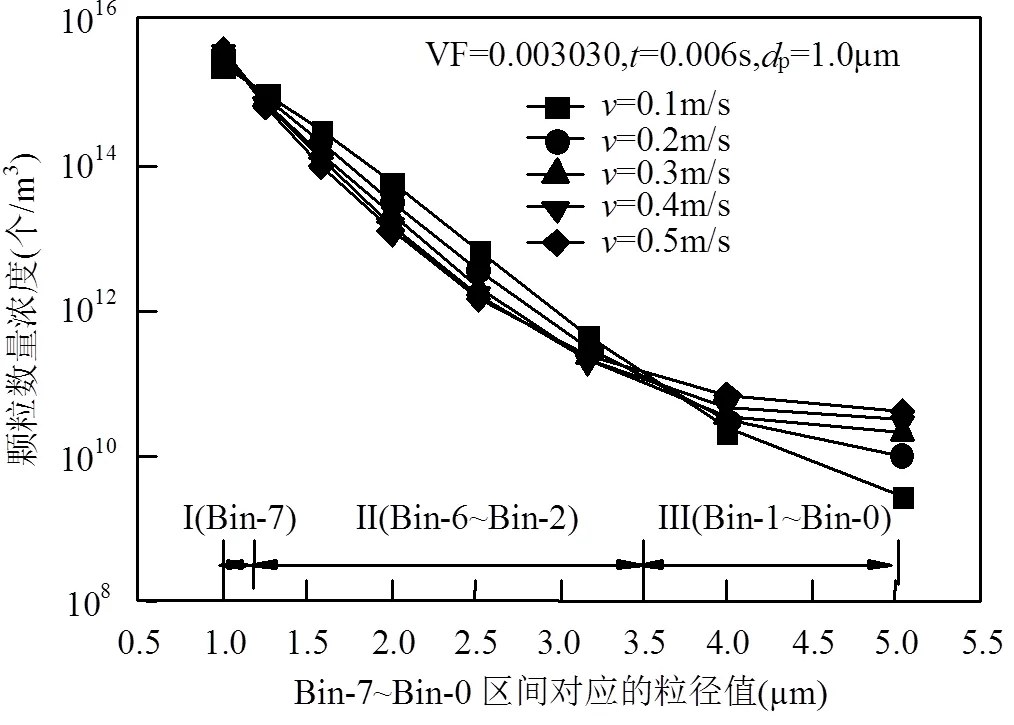
图6 入口风速对颗粒湍流团聚的影响

图7(a)表示Bin-7区间颗粒数量浓度在不同入口风速下随停留时间变化曲线.入口风速越大,Bin-7区间颗粒数量浓度随停留时间下降越快,即团聚速率越大,但稳定后Bin-7区间颗粒数量浓度越大,这是因为速度增大导致颗粒在纤维捕集结构中停留时间减少.通过图7(b)和(c)可知,速度越大,粉尘颗粒的团聚速率越大,唯一不同的是稳定后7(b)中颗粒数量浓度大小与速度大小呈负相关,7(c)中呈正相关,根据图5的规律,Bin-0相比于Bin-3区间颗粒粒径较大,单位时间内的Bin-0区间数量浓度变化百分比要大于Bin-3区间,速度增加导致停留时间减小,对于7(b)中的小颗粒,速度增加导致的颗粒数量浓度的增加量小于因为停留时间减小损失的颗粒数增加量;对于7(c)中的大颗粒,速度增加导致的颗粒数量浓度的增加量大于因停留时间减小损失的颗粒数增加量.

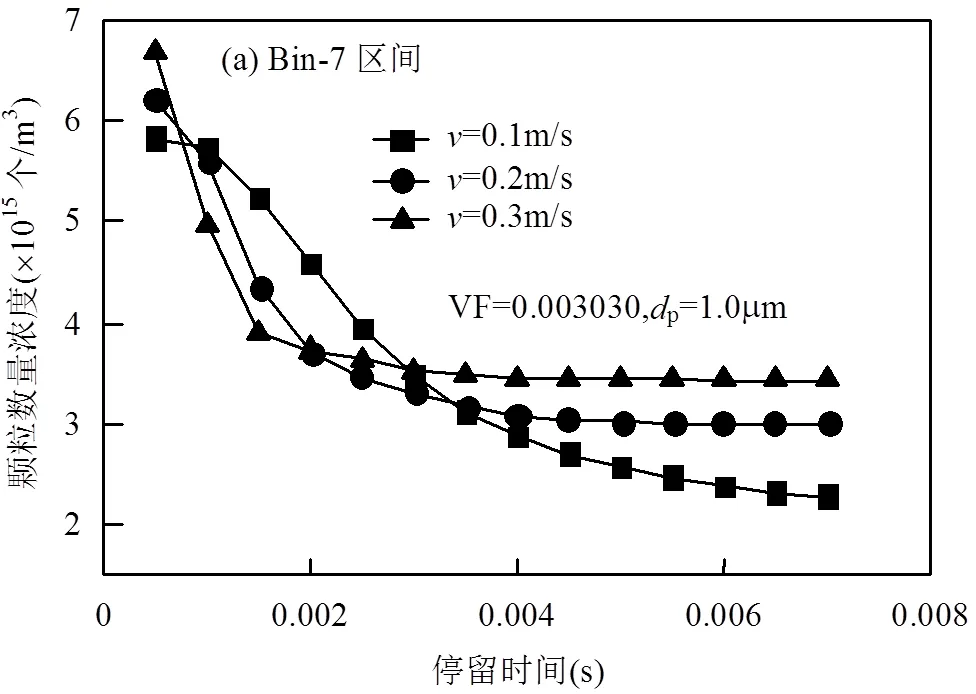
随着入口风速的增加,湍流耗散率是逐渐增加的,由于在湍流团聚核中,颗粒的团聚与湍流耗散率成正比,故湍流耗散率越大,粉尘颗粒的团聚速率越大,但最终的团聚效果取决于入口风速和粉尘颗粒在流场中的停留时间,当max·£,入口风速越大,颗粒团聚程度越大.

4.3 捕集过程中入口粒径对颗粒湍流团聚的影响

由图8可知,入口粒径越大,团聚稳定后Bin-7区间与Bin-0区间颗粒数量浓度的数量级差距越大,说明入口粒径越大,粉尘颗粒的团聚程度越小.

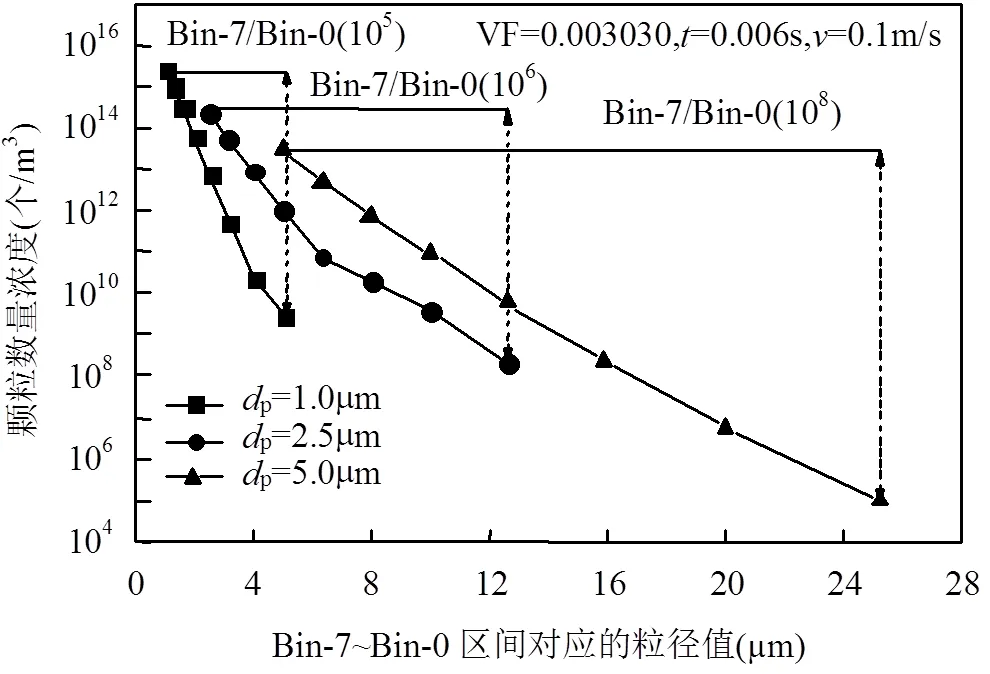
图8 粉尘粒径对颗粒湍流团聚的影响

由图9可知,出口平均粒径随时间都呈现先增加后趋于平稳的趋势,不同粒径的粉尘颗粒达到团聚稳定的时刻不同,入口粉尘颗粒粒径越大,流场中的颗粒数目越少,相同时间内碰撞几率减小,团聚速率减小.同时,出口处平均粒径与原粒径相比增加的倍率越小,这是因为颗粒粒径越小,扰动性越强,在流场中跟随性好,使得流场中的粉尘颗粒更容易发生碰撞,而对于大粒径颗粒,不容易受到扰动, 在流场中跟随性较差,再加上流场中的颗粒数目由于粒径增大减少,直接导致颗粒间碰撞几率减小,颗粒的团聚程度减小.

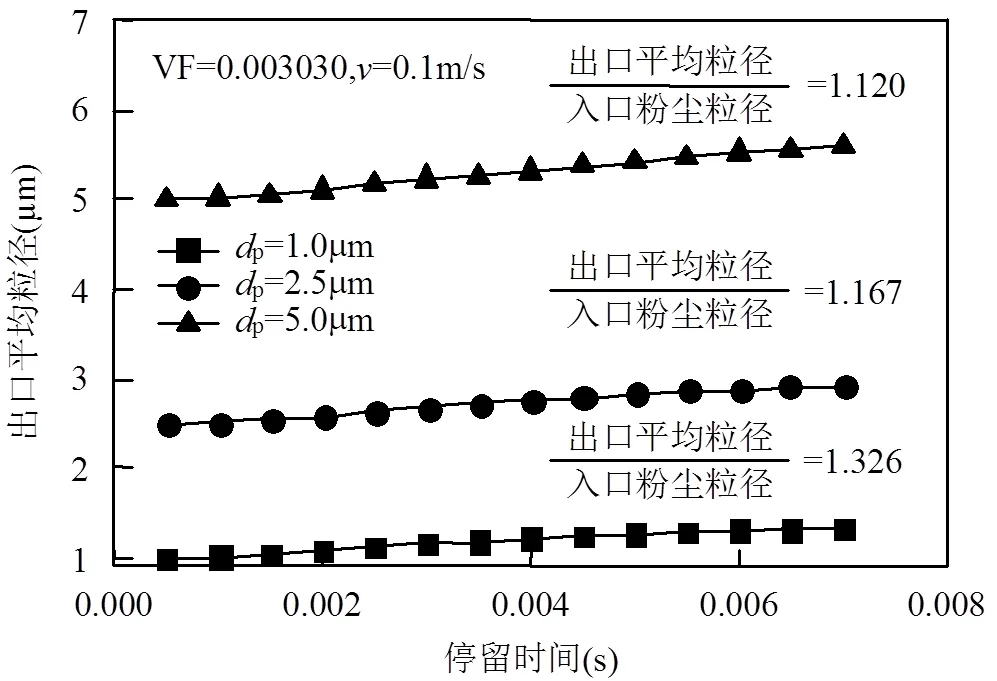
图9 出口平均粒径随停留时间变化曲线

4.4 捕集过程中体积分数对颗粒湍流团聚的影响

图10表明,粉尘颗粒的体积分数越大,粉尘颗粒在流场中的团聚效果越明显,团聚程度越大.这是由于粒径不变时,体积分数增大直接导致流场内颗粒数目增加,增加了粉尘颗粒碰撞的几率.同时,粉尘颗粒体积分数越大,单位时间内Bin-7区间颗粒数量浓度下降越快,即向大颗粒转化的速度越快,说明粉尘颗粒体积分数越大,粉尘颗粒的团聚速率越大,团聚程度越大.当=0.1m/s,p=1.0μm, VF>0.03636, Bin-7～Bin-0的颗粒数量浓度对数分布成线性比例关系.

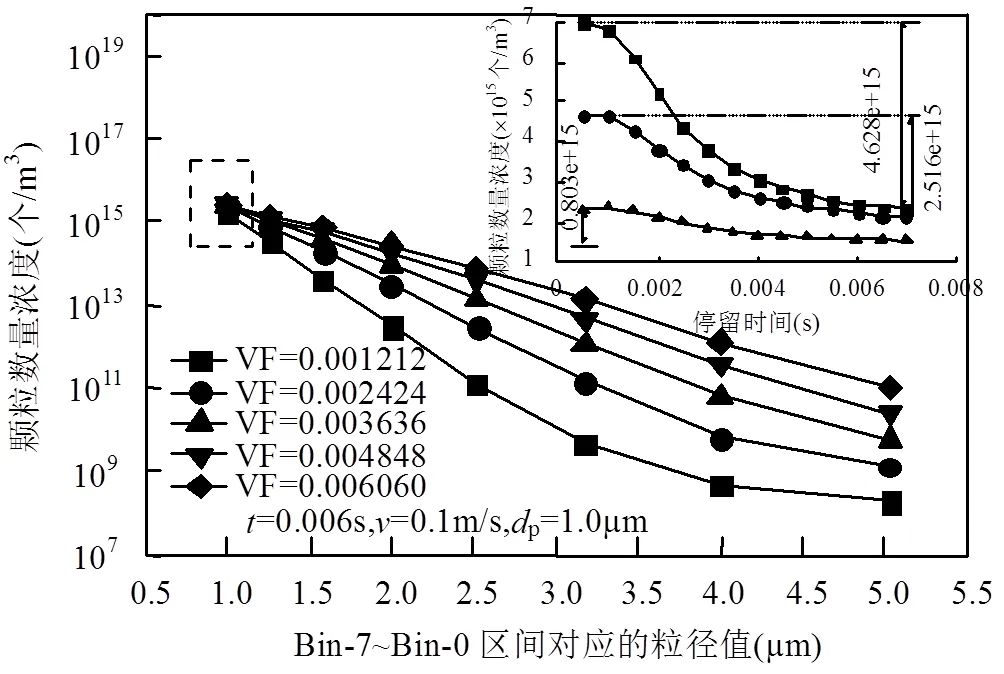
图10 粉尘体积分数对颗粒湍流团聚的影响

5 结论

5.1 粉尘颗粒在流场的作用下碰撞后受范德华力的作用发生湍流团聚,粒径逐渐向大颗粒偏移,当³/,团聚逐渐趋于稳定.小粒径段颗粒相比较于大粒径段颗粒团聚速率较大. 但单位时间内小粒径段颗粒数量浓度变化百分比较小.

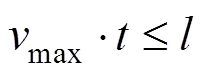
5.3 入口初始粉尘粒径越大,出口处平均粒径与初始粒径相比增加的倍数越小,即团聚程度和团聚速率越小;粉尘颗粒体积分数越大,颗粒之间碰撞的几率越大,粉尘颗粒的湍流团聚速率以及团聚程度越大,当=0.1m/s,p=1.0μm,VF>0.03636,Bin-7～Bin-0的颗粒数量浓度对数分布成线性比例关系.

[1] Li W, Shen S N, Li H, et al. Study and optimization of the filtration performance of multi-fiber filter [J]. Advanced Powder Technology, 2016,27:638-645.

[2] Zhu X J, Qian F P, Lu J L, et al. Numerical study of the solid volume fraction and pressure drop of fibrous media by response surface methodology [J].Chemical Engineering & Technology, 2013,36(5): 788-794.

[3] Saleh A M, Hosseini S A, Vahedi Tafreshi H, et al. 3-D microscale simulation of dust-loading in thin flat-sheet filters: A comparison with 1-D macroscale simulations [J].Chemical Engineering Science, 2013, 99(32):284-291.

[4] Yue C, Zhang Q, Zhai Z Q. Numerical simulation of the filtration process in fibrous filters using CFD-DEM method [J]. Journal of Aerosol Science, 2016,101:174-187.

[5] Qian F P, Huang N J, Zhu X J, et al. Numerical study of the gas-solid flow characteristic of fibrous media based on SEM using CFD-DEM [J]. Powder Technology, 2013,249:63-70.

[6] Subrenat A, Bellettre J, Cloirec P L. 3-D numerical simulations of flows in a cylindrical pleated filter packed with activated carbon cloth [J]. Chemical Engineering Science, 2003,58(22):4965-4973.

[7] Chen D R, Pui D Y H, Liu B Y H. Optimization of pleated filter designs using a finite-element numerical model [J]. Aerosol Science and Technology, 1995,23(4):579-590.

[8] Bucher T M, Tafreshi H V, Tepper G C. Modeling performance of thin fibrous coatings with orthogonally layered nanofibers for improved aerosol filtration [J]. Powder Technology, 2013,249:43-53.

[9] Hosseini S A, Tafreshi H V. 3-D simulation of particle filtration in electrospun nanofibrous filters [J]. Powder Technology, 2010,201(2): 153-160.

[10] Zhou J W, Zhang L, Zhang B, et al. Study on filtration performance of elliptical fiber with different arrangements [J]. Journal of Engineered Fibers and Fabrics, 2020,15:1-11.

[11] Che Y, Tian Z, Liu Z, et al. A CFD-PBM model considering ethylene polymerization for the flow behaviors and particle size distribution of polyethylene in a pilot-plant fluidized bed reactor [J]. Powder Technology, 2015,286:107-123.

[12] Cai L L , Liu Z Q , Mi S , et al. Investigation on flow characteristics of ice slurry in horizontal 90° elbow pipe by a CFD-PBM coupled model [J]. Advanced Powder Technology, 2019,30(10):2299-2310.

[13] 郑建祥,许 帅,王京阳.基于CFD－PBM积分矩量法旋风分离器中颗粒聚团的数值模拟 [J]. 流体机械, 2016,44(11):30-35.

Zheng J X, Xu S, Wang J Y. Numericle simulation of particle aggregation in cyclone separator using quadrature method of moments in CFD-PBM [J]. Fluid Machinery, 2016,44(11):30-35.

[14] 潘 伶,杨燕珍.袋式除尘器内部流场的数值模拟 [J]. 环境工程学报, 2012,6(8):2750-2754.

Pan L, Yang Y Z. Numerical simulation of flow field in bag filter [J]. Chinese Journal of Environmental Engineering, 2012,6(8):2750-2754.

[15] 张文斌,祁海鹰,由长福,等.碰撞诱发颗粒团聚及破碎的力学分析 [J]. 清华大学学报(自然科学版), 2002,42(12):1639-1643.

Zhang W B, Qi H Y, You C F, et al. Mechanical analysis of agglomeration and fragmentation of particles during collisions [J]. Journal of Tsinghua University (Science and Technology), 2002, 42(12):1639-1643.

[16] Piskunov V N, Golubev A I, Barrett J C, et al. The generalized approximation method for modeling coagulation kinetics-Part 2: Comparison with other methods [J]. Journal of Aerosol Science, 2002, 33(1):65-75.

[17] Saffman P G, Turner J S. On the collision of drops in turbulent clouds [J]. Journal of Fluid Mechanics, 1956,1(1):16-30.

[18] 斯奈德D L.随机点过程 [M]. 北京:人民教育出版社, 1982, 325−336.

Snyder D L. Random point processes [M]. Beijing: People's Education Press, 1982:325−336.

[19] Van Lieshout M N M. An introduction to planar random tessellation models [J]. Spatial Statistics, 2012,1:40−49.

[20] 黄乃金,钱付平,查文娟,等.基于微观结构的褶式滤芯拟态化模型及其过滤性能的数值模拟 [J]. 过程工程学报, 2014,14(3):402-408.

Huang N J, Qian F P, Zha W J, et al. Modeling of the pleated filter based on microscopic structure and numerical simulation of its filtration characteristics [J]. The Chinese Journal of Process Engineering, 2014,14(3):402-408.

[21] Hosseini S A, Tafreshi H V. On the importance of fibers' cross- sectional shape for air filters operating in the slip flow regime [J]. Powder Technology, 2011,212(3):425-431.

[22] Gelbard F. Sectional representations for simulating aerosol dynamics [J].Journal of Colloid and Interface science, 1980,76:541-556.

[23] Davies C N. Air filtration [M]. New York: Academic Press Inc, 1973.

[24] Happel J. Viscous flow relative to arrays of cylinders [J]. AIChE Journal, 1959,5(2):174-177.

[25] Kuwabara S. The forces experienced by randomly distributed parallel circular cylinders of spheres in a viscous flow at small Reynolds number [J]. Journal of the Physical Society of Japan, 1959,14(14): 527-532.

[26] Rao N, Faghri M. Computer modeling of aerosol filtration by fibrous filters [J]. Aerosol Science and Technology, 1988,8(2):133-156.

[27] 张俪安,刁永发,楚明浩,等.单纤维捕集过程中亚微米颗粒的布朗团聚[J]. 中国环境科学, 2021,41(4):1548-1554.

Zhang L A, Diao Y F, Chu M H, et al. Brownian aggregation in the process of submicron particles captured by single fiber [J]. China Environment Science, 2021,41(4):1548-1554.

Study on turbulent aggregation characteristics in the process of fine-particle captured by multi-fiber.

ZHANG Li-An1, DIAO Yong-fa1*, CHU Ming-Hao1, JIA Zhong-Jian1, SHEN Heng-Gen1, SUN Jing2

(1.School of Environmental Science and Engineering College, Dong Hua University, Shanghai 201620, China；2.Gansu Lanfei Environment Protection Co., Ltd. Lanzhou 730030, China)., 2021,41(10)：4572～4578

This paper established the flat 3-D mimic structure that was based on the random multi-fiber filter media algorithm. The computational fluid dynamics-population balance model (CFD-PBM) was used to simulate the turbulent aggregation of fine particles during the multi-fiber capture. The partition method was used to solve the population balance equation (PBE). The analysis by the controlled variable method shows that there was apparent particle aggregation behavior in the multi-fiber capturing process. The particle aggregation degree increased with the increasing residence time and gradually stabilizes while³/(dimensional length along with the flow field direction/inlet velocity). Whenmax·£, the larger the velocity inlet, the larger the particle aggregation degree and the aggregation rate, but the final aggregation degree depends on the velocity inlet and residence time; the larger the particle diameter, the smaller the particle aggregation degree and the aggregation rate. Also, the smaller the ratio of the average particle diameter of the outlet compared with the initial particle diameter. The larger the volume fraction of dust particles, the larger the particle aggregation degree and the aggregation rate. When=0.1m/s,p=1.0μm, VF > 0.003636, the number concentration logarithmic distribution between Bin-7～Bin-0 shows a linear proportional relationship.

computational fluid dynamics-population balance model；population balance equation；partition method；turbulent aggregation；multi-fiber

X513

A

1000-6923(2021)10-4572-07

张俪安(1990-),男,安徽省淮北人,东华大学博士研究生,主要从事工业烟气PM2.5控制技术研究.发表论文4篇.

2021-02-09

国家重点研发计划项目(2018YFC0705300);中央高校基本科研业务费重点项目(2232017A-09);中央高校基本科研业务费专项资金、东华大学研究生创新基金项目(CUSF-DH-D-2020067);兰州市人才创新项目(2019-RC-7)

* 责任作者, 教授, diaoyongfa@dhu.edu.cn