基于MATLAB的锂离子电池SOC相关参数辨识

李晓锋

（郑州工程技术学院 机电与车辆工程学院，河南郑州 450037）

引言

石油是一种不可再生能源，其作为传统燃料应用于车辆上，一方面加剧了能源危机，另一方面也产生了大量的污染，使生态环境恶化。与传统汽车相比，电动汽车是新能源汽车家族中比较重要的一员，因其独特的优势越来越受到重视。电动汽车的动力来源是电池，因此对电池能量状态的精确计算十分重要，常用SOC（state of charge）作为电池的量度指标[1]；SOC表示电池中可提取的剩余容量与总容量的百分比，类似传统汽车的燃油表。因此SOC的精确估计对电池设计人员和电池用户至关重要。然而，电池的容量受很多因素的影响，如充放电电流、放电时间、放电终止电压、电解液温度、电池存储时间、电池使用周期等。

近年来，人们提出了许多估算电池SOC的方法，典型的方法有：（1）安时积分法：通过测量电流对时间积分，这种方法会因电流测量的精确度和电池的老化而导致误差越来越大，需要定期校准；（2）开路电压法：利用开路电压OCV与SOC之间的相关曲线来间接测量SOC，OCV的大小受电池静置时间的影响，对车辆运行中SOC的估计会产生较大误差[2]。

目前对SOC估计采用最多是卡尔曼滤波算法以及由其衍生出的扩展卡尔曼算法、无迹卡尔曼算法、自适应卡尔曼算法等。无论哪一种算法，都是以等效电路模型为基础，通过辨识相应的参数，然后再进行相应的计算得到[3]，本研究主要通过使用分层技术与MATLAB拟合工具箱相结合，对参数进行辨识[4]。

1 常用的等效电路模型

电池的充放电过程，是化学能和电能相互转化的过程。在对电池SOC估算之前，需要建立适合的电池模型。常见的锂离子电池模型有化学模型、神经网络模型和等效电路模型。等效电路模型是将电池内部的化学反应过程用电压、电阻、电容等电学元件来模拟电池的对外输出特性。等效电路模型又有Rint模型、PNGV模型、Thevenin模型和RC模型等[5]。RC模型又根据RC关联支路个数的不同，有整数阶（如一阶RC等效电路模型、二阶RC等效电路模型、三阶RC等效电路模型等）和分数阶等[6]。考虑到精度和计算量两方面的特点，本研究采用二阶RC等效电路模型。如图1所示。

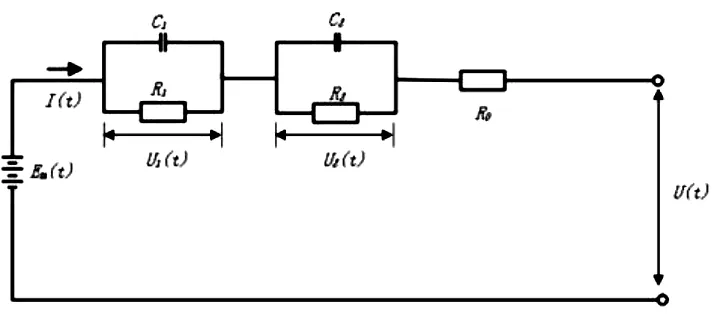
图1 2阶RC等效电路模型

由图1，根据基尔定律，可得出如下方程：

图中：Em是电压源，R0为电池内阻，R1、C1分别为表征欧姆极化的极化电阻和极化电容，R2、C2分别为表征浓差极化的极化电阻和极化电容，U(t)为电池端电压。本研究忽略了电池自放电对端电压U(t)的影响。图中的 Em、R0、R1、C1、R2、C2参数都不是定值，会随着电池的状态发生变化。下面对式（1）中的Em、R0、R1、C1、R2、C2通过试验进行分析辨识。

2 试验结果

通过对18650锂离子电池做脉冲放电试验，得到相应的试验数据，结合分层技术和MATLAB对上述参数进行辨识。在本试验中，采用的试验设备为新威分容柜；试验电池的额定容量为2000 mAh，额定电压4.2 V，采用脉冲放电倍率为1 C，即2000 mA，每次放电时间为10 min（即每次放出10%的容量），然后停置60 min，放电终止电压设置为3.2 V，获得的试验图形如图2所示。

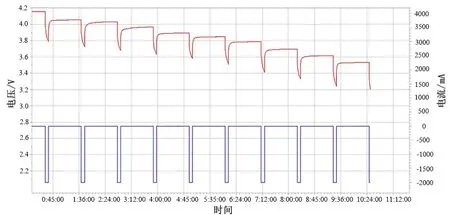
图2 放电试验电压、电流与时间的关系曲线

3 参数辨识

选取任一SOC下的脉冲响应进行分析，如图3所示。从图3所示脉冲图形中可以看出开路电压Em和电池内阻 R0的变化以及 R1、C1、和 R2、C2的响应，其他SOC下的脉冲响应与此类似。

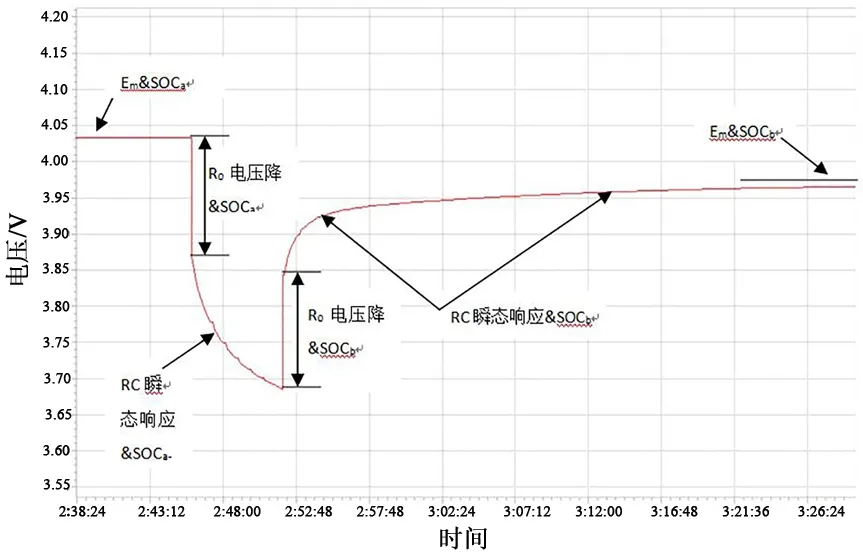
图3 任一SOC下的脉冲图形

分析每个脉冲下的数据，可以得到开路电压Em与SOC的一一对应关系（见表1），并通过MATLAB曲线拟合工具箱进行多项式拟合[7]，可以得到Em与SOC的多项式关系（见公式（1））和相应的图形关系（如图4）。

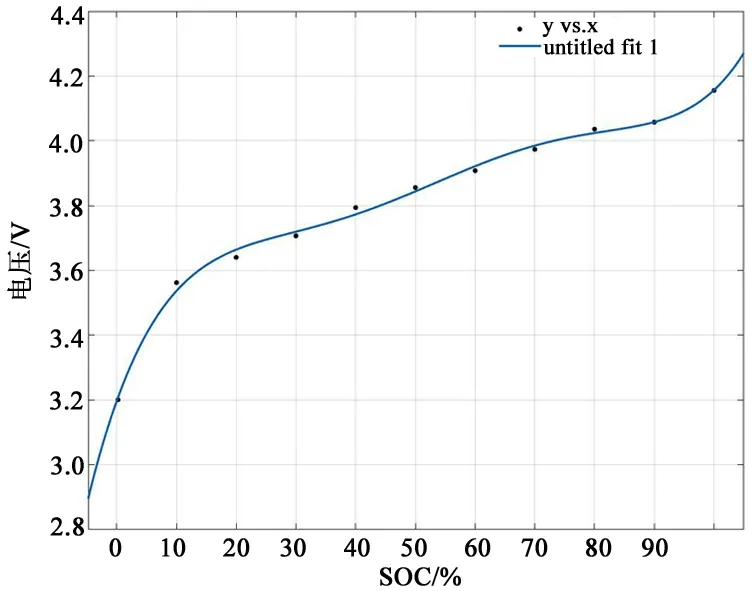
图4 Em与SOC的关系曲线

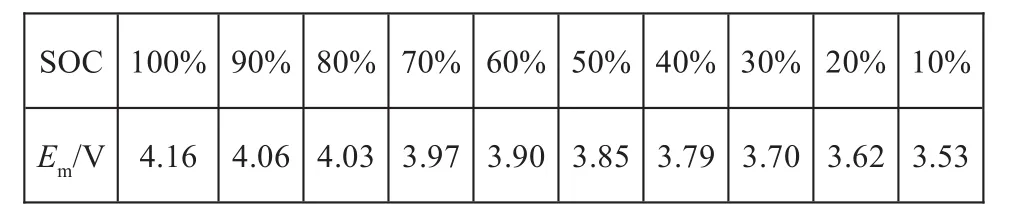
表1 开路电压Em与SOC的对应关系

开路电压Em与SOC的多项式关系：

3.1 利用分层技术辨识R0

由于试验数据量太大，而且每个SOC下的脉冲响应都有相似的特点，可以把数据按照每个脉冲或每个级别的SOC进行分类评估，即所谓分层技术[9，10]，具体如图5所示。

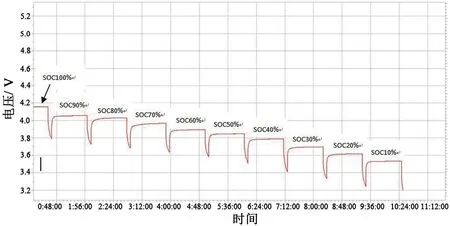
图5 分层估计技术图形

利用上述的分层技术，求得第一个SOC级别下的内阻R0，对每个SOC级别下的R0取平均值，可得到R0和SOC的一一对应关系，然后通过拟合工具箱进行拟合，可以得到R0和SOC的图形关系，如图6所示。

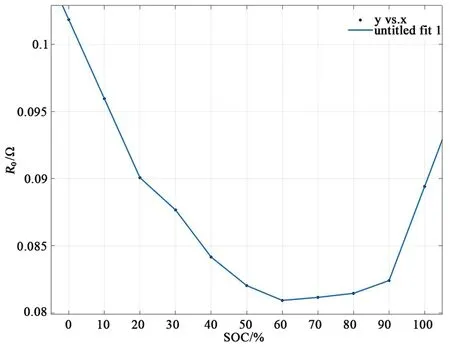
图6 Rm与SOC的关系曲线

3.2 时间常数τ1和τ2的参数辨识

在脉冲放电过程中，RC的动态响应属于零输入响应，对应的公式如下：

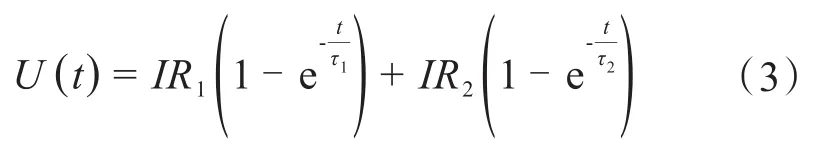
在停置过程中的RC响应属于零输入响应，对应的公式如式（4）所示。

把静置过程中的试验数据导入MATLAB曲线拟合工具箱，按照指数零输入响应公式进行拟合，可以得到 τ1和τ2的数值。得到的τ1和τ2的数值和SOC的一一对应关系如表2所示，相应的图形如图7，8所示。

图7 时间常数τ1与SOC的关系

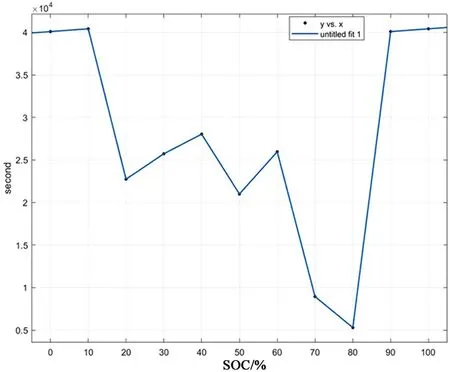
图8 时间常数τ2与SOC的关系

表2 时间常数τ1，τ2与SOC的一一对应关系

3.3 R1、R2的参数辨识

将每个SOC级别下脉冲放电数据导入MAT‐LAB曲线拟合工具箱，把求得的τ1和τ2的数值代入零状态响应指数公式，可拟合出每个SOC级别下的R1和R2的值，如表3所示，相应的图如图9，10所示。

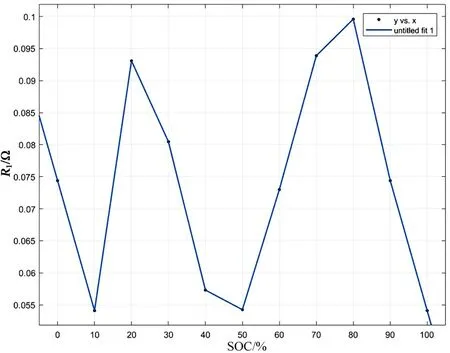
图9 R1与SOC的关系

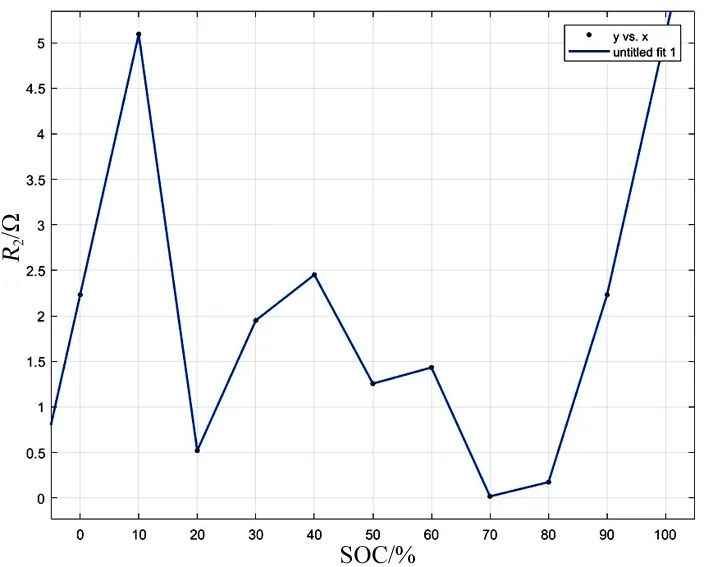
图10 R2与SOC的关系

3.4 C1、C2的参数辨识

利用公式τ=RC，结合表2和表3中所得到的每个 SOC 级别下的 τ1、τ2和 R1、R2可得到相应的 C1、C2，结果如表4所示，相应的图形如图11，12所示。

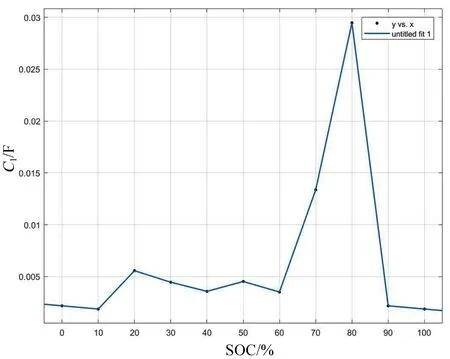
图11 C1与SOC的关系

表3 R1，R2与SOC的一一对应关系

表4 C1，C2与SOC的一一对应关系

图12 C2与SOC的关系

4 结束语

详细介绍了对SOC估算前需要进行的相关参数辨识，利用MATLAB得到了各参数与SOC之间的关系。接下来的任务是通过卡尔曼滤波算法对SOC进行在线最优估计，这是后续研究的主题内容。