溴化镧探测器探测效率刻度及影响因素分析

杨体波 王 敏 代光明 曹 彧 廖光辉 范新洋

（成都理工大学核技术与自动化工程学院 成都 610059）

计算地层中各元素的含量、确定矿物成分是地质矿产勘探中的一项重要工作。随着测井技术的发展，基于核探测与分析的地层元素测井［1−4］技术在地层岩性识别中得到了较为广泛的应用。由于具有能量分辨率高、温度性能好等诸多优点［5−6］，溴化镧探测器（LaBr3:Ce晶体）在地层元素测井中取代了传统的碘化钠探测器。在地层元素测井中，所需要测量的俘获γ 射线与非弹性γ 射线的能量范围较大（100 keV～10 MeV），一般实验室所用的放射源发出的γ 射线的能量在2 MeV 以下，如果采用有源效率刻度，难以实现高能区的刻度［7］。无源效率刻度则是一种快捷、方便、准确的方法，利用蒙特卡罗软件，可以实现对溴化镧探测器的无源效率刻度，确定出γ射线全能峰效率与能量之间的关系曲线。全能峰效率是评价探测器性能好坏的一项重要指标，影响全能峰效率的因素有很多，比如γ射线的能量、晶体尺寸、反射层厚度、外壳厚度等。钟丁生等［8］使用MCNP（Monte Carlo N Particle Transport Code，基于蒙特卡罗方法的用于计算三维复杂几何结构中的中子、光子、电子或者耦合中子/光子/电子输运问题的通用软件包）软件研究了溴化镧探测器几何因素对探测效率的影响，结果表明：增大晶体的几何尺寸，探测效率增大，当晶体尺寸增大到一定程度时，探测效率值趋于稳定；谢希成等［9］利用MCNP 软件模拟了不同尺寸溴化镧晶体的全能峰探测效率，与实验所得值进行对比，其误差在7%以内，并且通过拟合得到了点源效率函数；邓中华等［10］利用MCNP 软件通过模拟获得了溴化镧探测器能量线性曲线、探测效率曲线，与实验值的相对误差在5%以内；姚剑峰等［11］通过MCNP 模拟获得了不同探测器厚度、晶体半径以及源距对应的全能峰效率，实现了对探测器的无源效率刻度；卢毅等［7］采用蒙特卡罗方法计算了不同尺寸溴化镧闪烁体的吸收效率以及峰总比曲线，并 对ø50 mm×10 mm 的LaBr3: Ce 探测器在0～10 MeV 的能段进行了效率刻度；Favalli 等［5］研究了LaBr3: Ce 闪烁探测器在宽能量范围（200～5 000 keV）下的全能峰效率；Yang 等［12］基于高纯锗探测器比较了三种效率刻度方法，即实验室有源效率刻度、实验室无源效率刻度软件、半经验公式与数值模拟相结合，证明了有源效率刻度是最准确的方法，同时，随着高效计算技术的进步，无源效率刻度、半经验公式和数值模拟相结合的方法仍有望得到更广泛的运用。

以上研究中，对探测器进行无源效率刻度时，只是考虑了晶体尺寸的大小、源距等参数对全能峰效率的影响，并没有考虑反射层厚度以及探测器外壳厚度对全能峰效率的影响；在研究晶体尺寸大小对全能峰效率的影响时，也没有分析晶体长度与晶体半径对全能峰效率的具体影响。在此基础上，本文利用MCNP 软件研究了反射层、探测器外壳、晶体半径、晶体长度对全能峰效率的影响，并根据模拟结果选择最优参数，针对地层元素测井中所使用的溴化镧探测器（LaBr3: Ce 晶体尺寸为ø3.18 cm×10.16 cm）进行了无源效率刻度。

1 理论基础与模型建立

1.1 理论基础

全能峰效率εp定义为γ谱全能峰下包含的计数与放射源在相同时间内发射的γ 射线计数的比值［13］，即：

式中：Npeak为全能峰计数，即能谱上全能峰的面积；Nγ为放射源发出的γ 射线总计数。实测时，根据能谱找到所需要的全能峰和对应的道址范围，计算其面积，再减去本底计数即可得到全能峰计数，也可以直接通过测量软件读出全能峰计数。利用MCNP 软件进行模拟时，通过输出文件读出归一化的概率即可得到全能峰效率。全能峰效率是描述探测器性能的一个重要指标，它主要与探测器的种类、γ射线的能量以及测量时的源距等因素有关，利用式（2）［14］可以计算全能峰效率值：

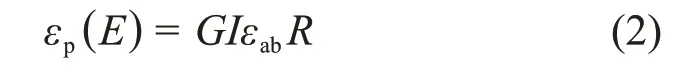
式中：G为几何效率；I表示放射源发出的γ射线经探测器Al壳、MgO反射层衰减后到达探测器晶体表面时的强度因子；εab为探测器晶体对γ 射线的吸收效率，对于不同能量的γ射线，其吸收效率不同；R为峰总比，即探测器的输出能谱中，全能峰计数与总计数的比值，也可以通过MCNP软件模拟得到。I可以通过式（3）［15］计算得出；

式中：μ为线性衰减系数，cm−1；x为衰减物质的厚度，cm，在计算时μ、x分别对应探测器Al壳和MgO反射层的线性衰减系数和厚度。吸收效率εab由式（4）［14］计算：

此时，μ、x使用LaBr3:Ce 晶体的线性衰减系数、厚度；几何效率G由式（5）［14］计算得到：

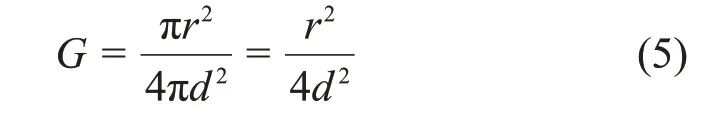
式中：r为探测晶体的半径，cm；d为源距，cm，即源到探测器之间的距离。线性衰减系数μ与质量衰减系数μm的关系可以由式（6）［16］得出：

式中：ρ为衰减物质的密度，g∙cm−3；μm为质量衰减系数，cm2∙g−1，可以通过WinXcom软件获得。

1.2 模型建立

参考实际的溴化镧探测器尺寸，在MCNP 中构建的探测器模型如图1所示。以探测器Al壳左端面圆心为原点（0，0，0），点源位置设置为（−5，0，0），源距为5 cm，模拟能量为0.662 MeV的137Cs源，溴化镧晶体直径为3.18 cm，晶体长度为10.16 cm，晶体外面包裹一层MgO反射层，其厚度为0.05 cm，最外层为Al壳，其端面厚度为0.1 cm，侧面厚度为0.25 cm，右侧端面为SiO2光导，厚度为0.2 cm。计数卡采用F8脉冲计数卡，将能量划分为1 024道来记录γ光子的能量分布，模拟运输的粒子数为5×107。

图1 溴化镧探测器模型Fig.1 Model for the lanthanum bromide detector in the MCNP calculation

2 探测效率影响因素

本文主要研究溴化镧探测器的端面Al壳厚度、侧面Al 壳厚度、MgO 反射层厚度、晶体长度以及晶体半径等参数对全能峰效率的影响。

2.1 端面Al壳厚度对全能峰效率的影响

研究端面Al 壳厚度对全能峰效率的影响时，γ射线能量设置为0.662 MeV，源距为5 cm，MgO反射层厚度为0.05 cm，侧面Al壳厚度为0.25 cm，只改变端 面Al 壳的 厚度（0.05 cm、0.10 cm、0.15 cm、0.20 cm、0.25 cm、0.30 cm、0.35 cm、0.40 cm），结果如图2所示。

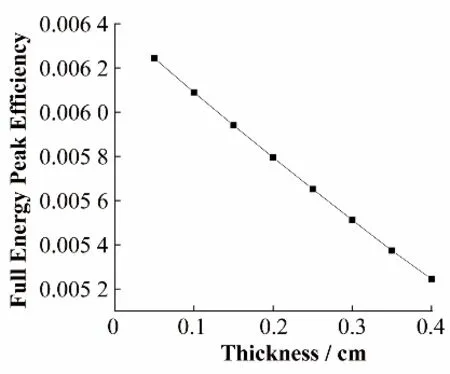
图2 端面Al壳厚度对全能峰效率的影响Fig.2 Effect of the thickness of Al shell in end-face of the detector on the full-energy peak efficiency

由图2可知，Al壳的厚度会影响全能峰效率；随着Al壳厚度的增加全能峰效率降低，设计探测器尺寸时，在考虑保护作用与屏蔽β射线的前提下，可以尽量降低Al壳的厚度，以提高全能峰探测效率。

2.2 侧面Al壳厚度对全能峰效率的影响

研究侧面Al 壳厚度对全能峰效率的影响时，γ射线能量设置为0.662 MeV，源距为5 cm，MgO反射层厚度为0.05 cm，端面Al 壳厚度为0.1 cm，只改变侧 面Al 壳的 厚度（0.05 cm、0.10 cm、0.15 cm、0.20 cm、0.25 cm、0.30 cm、0.35 cm、0.40 cm），结果如图3所示。

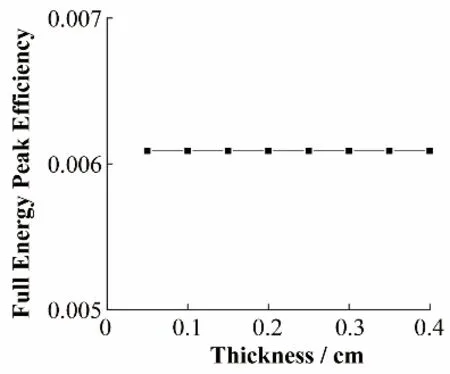
图3 侧面Al壳厚度对全能峰效率的影响Fig.3 Effect of the thickness of cylindrical Al shell of the detector on the full-energy peak efficiency

由图3可以看出，当端面Al壳厚度一定时，改变侧面Al壳的厚度不会影响全能峰探测效率，在地层元素测井中使用溴化镧探测器时，可以适当增加侧面Al壳的厚度以提高对探测器的保护效率。

2.3 MgO反射层对全能峰效率的影响

模拟MgO 反射层对全能峰效率的影响时，γ 射线能量设置为0.662 MeV，源距为5 cm，端面Al壳厚度为0.1 cm，侧面Al 壳厚度为0.25 cm，分别模拟了MgO 反射层的端面和侧面厚度同时为0.01 cm、0.03 cm、0.05 cm、0.07 cm、0.10 cm、0.15 cm、0.20 cm的情况，模拟结果如图4所示。

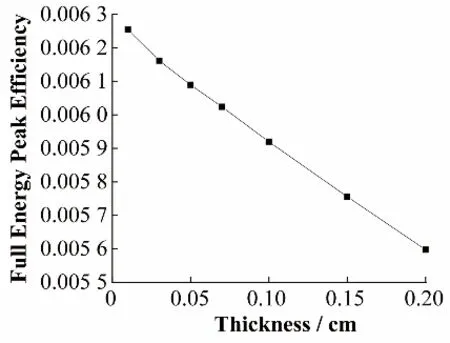
图4 MgO反射层对全能峰效率的影响Fig.4 Effect of the thickness of the MgO reflective layer on the full-energy peak efficiency

从图4 中可以看到，增加MgO 反射层的厚度，全能峰效率随之下降，其趋势呈一条直线，为了提高探测器的探测效率，在保证起到反射目的的情况下，可以降低MgO反射层的厚度，一般取0.05 cm。

2.4 晶体尺寸对全能峰效率的影响

LaBr3:Ce晶体尺寸大小对全能峰效率的影响主要包括两部分：晶体长度的影响和晶体半径的影响，模拟时γ 射线能量设置为0.662 MeV，源距为5 cm，端面Al壳厚度为0.1 cm，侧面Al壳厚度为0.25 cm，MgO 反射层厚度为0.05 cm，分别模拟了晶体长度为2.54 cm、5.08 cm、7.62 cm、10.16 cm，晶体半径为1.59 cm、3.81 cm、4.77 cm、6.36 cm、7.95 cm、9.54 cm、11.13 cm的情况，模拟结果如图5所示。

从图5 可以看出，在γ 射线的能量为0.662 MeV、源距为5 cm的情况下，随着晶体半径的增加，全能峰效率逐渐增加，但是增加的幅度越来越小。这是由于当晶体半径较小时，点源相对探头的立体角较小，几何效率较底；随着晶体半径的增加，点源相对探头的立体角增加，几何效率逐渐增加，从而全能峰效率也随之增加；当半径增加到某个数值后，再增加半径，其立体角的变化很小，此时全能峰效率的变化也较小。同时也可以看到，当晶体半径一定时，随着晶体长度的增加，全能峰效率也会增加。晶体长度的增加会使得γ射线与晶体发生反应的概率增加，更容易使其能量全部沉积于晶体中，进而提高全能峰效率。由于增加晶体半径比增加晶体长度对探测效率的提升更加显著，在地层元素测井中，如果地层孔径的尺寸允许，应尽量增加晶体半径大小以提高探测效率。

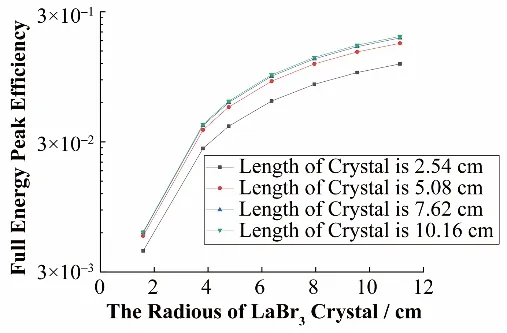
图5 晶体尺寸对全能峰效率的影响Fig.5 Effect of the LaBr3:Ce crystal size on the full- energy peak efficiency

为了进一步探究晶体半径以及晶体长度对全能峰效率的影响，分别改变晶体的长度与半径（1.27 cm、2.54 cm、3.81 cm、5.08 cm、6.35 cm、7.62 cm）进行模拟，晶体长度与半径的变化步长设置为1.27 cm，对比晶体长度和半径变化对全能峰效率的影响，所得结果如图6所示。

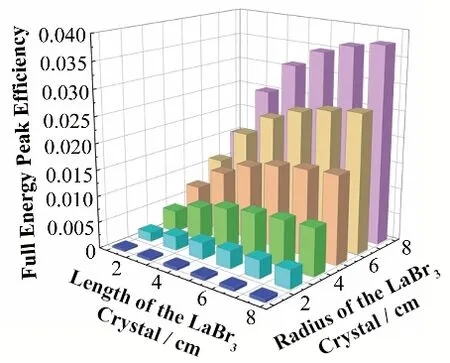
图6 对比晶体长度变化和半径变化对全能峰效率的影响Fig.6 Comparison of the effects of length and radius of the crystal on the full-energy peak efficiency

由图6 可知，晶体长度变化和半径变化对全能峰效率的影响并不相同，当半径较小时（<3.81 cm），晶体长度的变化对全能峰效率的影响较小；当晶体半径较大时（3.81～7.62 cm），随着晶体长度的增加，全能峰效率也随之增加，但增加的趋势逐渐减缓。晶体半径变化对全能峰效率的影响较大，随着晶体半径的增加全能峰效率也随之增加；相比于晶体长度较小（1.27 cm）的情况来说，当晶体长度较大时（>2.54 cm），晶体半径变化对全能峰效率的影响更显著。

3 效率刻度

对影响全能峰效率的因素进行研究和分析后，对溴化镧探测器进行了无源效率刻度，获得全能峰效率和能量之间的关系曲线。模拟时，源距设置为5 cm，端面Al 壳厚度为0.1 cm，侧面Al 壳为0.25 cm，MgO 反射层厚度为0.05 cm，LaBr3:Ce 晶体尺寸为ø3.18 cm×10.16 cm。对地层元素测井中的非弹性散射γ射线、俘获γ射线进行分析后，发现γ射线的能量主要分布在100 keV～10 MeV之间，因此将模拟的γ 射线能量设置为：0.1 MeV、0.3 MeV、0.5 MeV、0.8 MeV、1.0 MeV、1.5 MeV、2.0 MeV、2.5 MeV、3.0 MeV、3.5 MeV、4.0 MeV、4.5 MeV、5.0 MeV、6.0 MeV、7.0 MeV、8.0 MeV、9.0 MeV、10.0 MeV，结果如图7所示，通过拟合获得了刻度曲线及其参数，如式（7）所示：

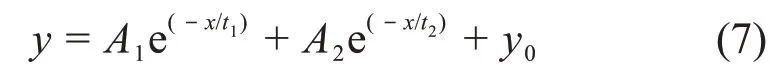
式中：y为全能峰效率；x为γ 射线的能量，MeV。其中，参数A1= 0.020 05，A2= 0.00394，t1= 0.382 65，t2= 2.78106，y0= 3.384 23 × 10−4。从图7 中可以看出，随着γ 射线能量的增加，全能峰效率呈下降趋势，这是由于能量越高的γ射线越容易穿透晶体，并没有在晶体中沉积能量而被记录下来，全能峰效率随之降低。

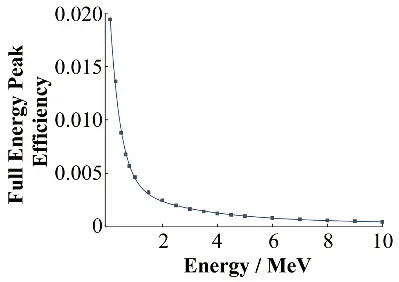
图7 溴化镧探测器全能峰效率刻度曲线Fig.7 Curve of full-energy peak efficiency calibration of the LaBr3 detector

为了确保模拟结果的准确性，首先通过理论公式计算进行验证。图8 为WinXcom 软件得到的LaBr3:Ce 晶体和Al 对不同γ 射线的质量衰减系数，由于MgO 的质量衰减系数图与Al的质量衰减系数图8（b）比较相似，避免重复而没有进行展示。通过式（6）可以求出LaBr3:Ce 晶体和Al 对不同γ 射线能量的线性衰减系数。

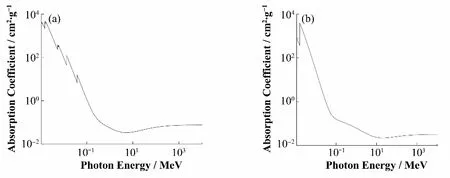
图8 LaBr3:Ce晶体(a)和Al (b)对不同能量γ射线的质量吸收系数Fig.8 Mass absorption coefficient of the LaBr3:Ce crystal (a) and Al (b) vs. gamma ray energy

通过MCNP模拟得到了不同能量的γ射线对应的峰总比，并与文献［14］中给出的标准数据进行了对比，在参考标准数据时，某些能量对应的峰总比在文献中并没有给出具体数值，根据拟合的曲线通过插值法得到。对于某些晶体来说，峰总比的值可以通过模拟的方式得到，在保证模型准确性的情况下，模拟数据可以直接用来计算全能峰效率。以上工作得到了LaBr3:Ce 晶体、Al、MgO 的质量衰减系数和峰总比，结合式（2～6）可以计算全能峰效率值（表1）。

通过表1 可以看出，峰总比的模拟值和理论值的误差在6% 以内，全能峰效率的模拟值与理论值的误差在7%以内，表明了模拟数据的可靠性。

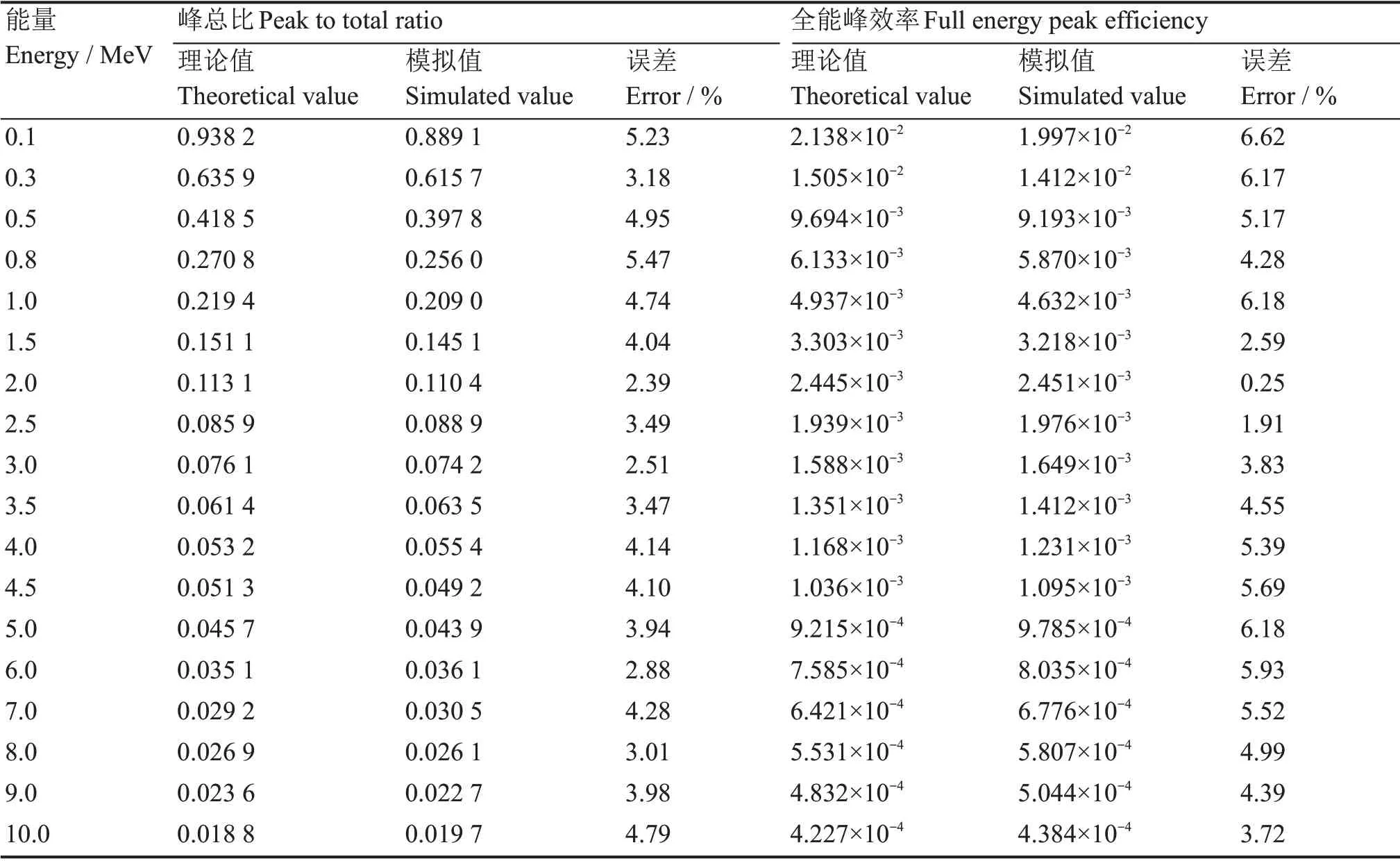
表1 峰总比和全能峰效率的模拟值与理论值Table 1 Simulated and theoretical values of peak to total ratio and full-energy peak efficiency of the LaBr3 detector

为了进一步验证数据的准确性，利用LaBr3:Ce探测器分别对152Eu、60Co、137Cs 源进行了测量，源距为5 cm，与模拟时的参数保持一致，根据测量的能谱计算了全能峰效率值，进行效率刻度。三种放射源发出的γ 射线能量主要在121.78～1 408.93 keV 之间，将其能量代入模拟得到的刻度曲线中，计算出全能峰效率值，与利用实测谱求得的全能峰效率进行对比，结果如表2所示。

从表2可以看出，实验值与模拟值的误差在6%以内，进一步证明了模拟的准确性。对于不具备有源效率刻度条件的实验室来说，无源效率刻度是一种可靠的方法。

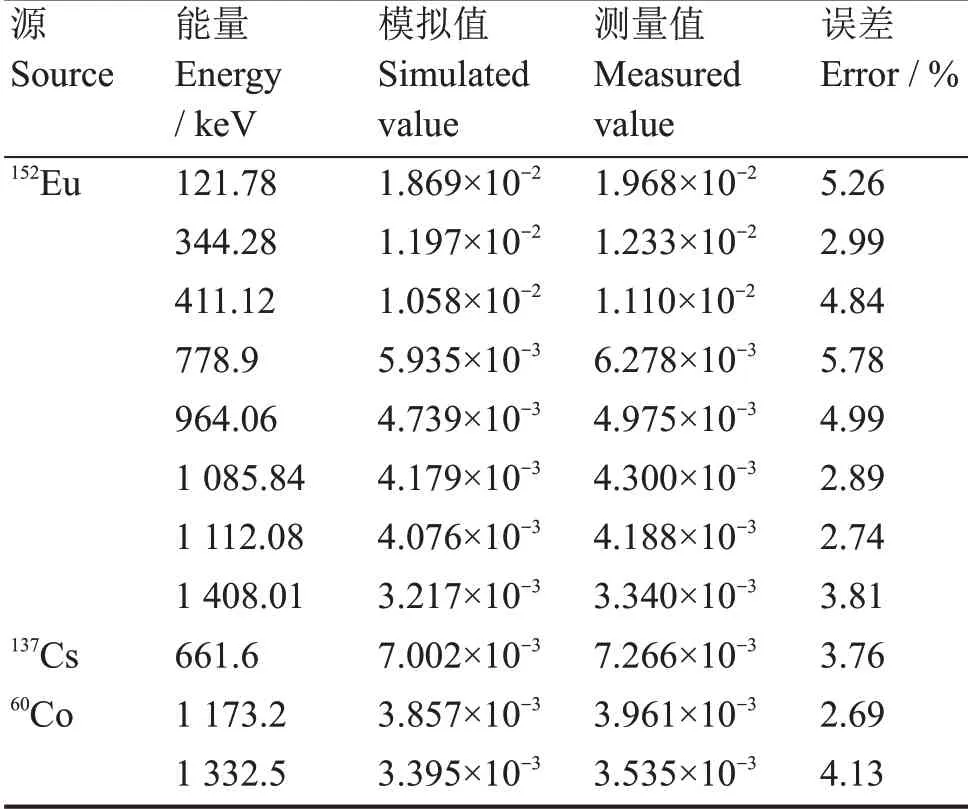
表2 全能峰效率实验值与模拟值Table 2 Simulated and measured values of full-energy peak efficiency of the LaBr3 detector

4 结语

运用MCNP5软件研究了溴化镧探测器Al壳厚度、MgO 反射层厚度、晶体长度和晶体半径对全能峰效率的影响，针对地层元素测井中使用的溴化镧探测器（LaBr3:Ce晶体，ø3.18 cm×10.16 cm），获得了100 keV～10 MeV能区的全能峰效率刻度曲线，并与理论计算结果和实测结果进行了对比，得出以下结论：

1）增加Al 壳厚度和MgO 反射层厚度会降低全能峰效率。

2）增加晶体的长度和半径都会提高全能峰效率，且晶体半径的变化对全能峰效率的影响较大；晶体长度变化对全能峰效率的影响效果在不同晶体半径时相差较大，当晶体半径较小时，长度变化对全能峰效率的影响较小，随着半径的增加，长度变化对全能峰效率的影响逐渐增加，但是增加的幅度逐渐降低。

3）为了提高探测效率，对于地层元素测井中使用的LaBr3:Ce探测器，在孔径允许的情况下，应尽量增加晶体的半径、降低端面Al 壳和MgO 反射层的厚度；为了更好地保护探测器，可以适当增加侧面Al壳的厚度。

4）全能峰效率刻度的模拟结果与理论计算结果和实测结果之间的误差分别在7%和6%以内，证明了模拟结果的可靠性，同时也为实验室进行无源效率刻度提供了一定的参考。