基于SA-BP算法的蒙西电力现货市场价格预测

王金鑫，蒋子彦，王 琪，李 东，于福荣，刘 海，任婧媛

（1.北京京能电力股份有限公司，北京 100020；2.华北电力大学，北京 102206）

0 引言

目前我国电力现货市场尚处于初步探索阶段，电价机制、报价机制、市场规则等尚未成熟，蒙西电力现货市场于2019-06-26正式投入模拟试运行。在市场条件下，准确预测电力现货市场的电价能够辅助发电企业开展高质量的报价决策工作，对发电企业具有重要意义。

目前，短期的电价预测方法主要有时间序列法、神经网络法、组合预测法以及混合预测法。时间序列法通常采用历史电价作为样本建立回归模型，再用样本外的数据进行模型测试及电价预测。文献[1-2]将电价序列分为工作日序列与节假日序列，对两种序列分别建立ARMA-GARCH模型，最后对电价进行预测。文献[3]在研究了电价的波动规律后，根据电价序列特点建立ARMAX模型，并采用ARMAX模型进行电价预测。然而由于影响电价的因素众多，仅考虑单一变量的ARMAX模型存在一定的局限性。人工神经网络可以通过模拟人类大脑结构与功能来处理多变量问题。文献[4]采用人工神经网络进行电价预测，但易陷入局部优化，且预测效果并未显著优于时间序列法。

鉴于仅通过单一模型进行电价预测具有局限性，有学者尝试利用多个模型从不同角度开展预测，再将预测结果组合起来，形成了组合预测法。还有学者直接将多个模型组合起来共同进行电价预测，提出了混合预测法。文献[5]利用多元线性回归模型和反向传播网络组合模型对电价分别进行预测，然后根据预测值和权系数求得最终结果。文献[6-12]采用基于人工神经网络的混合模型对电力市场短期电价进行预测，均取得良好的效果。以上文献均未对国内电力现货市场进行过短期电价预测。

本文结合蒙西电力市场的特征以及影响电价预测的因素，采用模拟退火算法（Simulated Anneal⁃ing，SA）与BP神经网络相结合的混合模型对蒙西电力市场实际电价数据进行短期预测。算例结果证明了本文所提出方法的有效性。

1 SA-BP神经网络电价预测算法

1.1 SA算法

SA算法是基于Monte-Carlo迭代求解策略的一种随机寻优算法，由Metropolis算法和退火过程两部分组成。SA算法源于固体退火原理，温度升高时，固体内部的粒子内能增大，变为无序状；当温度缓缓降至固体冷却，粒子内能降低，并逐渐变得有序；最后在常温时达到基态，内能最小，每个粒子温度达到平衡状态。

SA算法利用Metropolis准则来控制温度下降的过程，以求全局最优解。其计算见公式（1）：?式中：P（i）—转移概率；

E（i）—粒子在i状态时的能量；

E（j）—粒子在j状态时的能量；

T—粒子温度。

SA算法流程如图1所示。

图1 SA算法流程

1.2 BP神经网络算法

BP神经网络可以通过模拟人类大脑结构与功能来处理多变量问题，且具有良好的学习能力。BP神经网络由输入层、隐藏层、输出层组成，是一种单向传播的多层前向网络。其优点在于泛化能力良好，可以很好地处理非线性问题；仅通过自身的训练就能以给定的输入得到接近期望值的结果，无需给出输入与输出之间的映射关系。BP神经网络结构如图2所示。

图2 BP神经网络结构

1.3 SA-BP神经网络算法

BP神经网络在对阈值和权值调整时采用梯度下降法，这种方法使得误差只能往降低的方向进行，容易陷入局部最优化。BP神经网络对初始网络权重较为敏感，当初始化权重不同时，可能误差信号不是只向降低的方向进行，从而避免陷入局部最优化。

本文将BP神经网络中的梯度下降法与SA算法中的随机扰动相结合，生成一种新的神经网络阈值与权值调整方法，在利用梯度法降低BP神经网络误差的同时，借助SA算法来解决BP神经网络容易陷入局部最优的困境，改善BP神经网络的收敛特性，从而实现对电价的有效预测。其计算流程如图3所示。

图3 SA算法与BP神经网络混合模型流程图

具体实现如下：首先设定一个神经网络，令初始矩阵R=[R1R2R3R4]为神经网络的初始权值与阈值组成的矩阵。其中由输入层与隐藏层之间权值组成的列向量为R1；由神经网络隐藏层阈值组成的列向量为R2；隐藏层与输出层之间权值组成的列向量为R3，输出层组成的列向量为R4。当神经网络在采用梯度下降法训练后达到局部最优，其权值和阈值停止调整。此时权值与阈值组成的矩阵变为R（i）为使其跳出局部最优，进行随机扰动，再对权值和阈值重新进行调整。随机扰动公式见式（2）：

式中：R（i+1）—经扰动后神经网络权值和阈值组成的新矩阵，i=1，2，3，…，k（k为正整数）；

rrand—随机函数；

R（i）—经训练后神经网络权值与阈值组成的矩阵。

2 影响电价预测的因素分析

输入变量的选择及输入数据的处理对电价预测的准确性影响重大，因此就这两方面分别进行讨论，以提高电价预测精度。

2.1 输入变量的选择

电力现货市场中影响电价的因素诸多，如负荷水平、供给情况、历史电价、电网结构、环境因素等。事实上，两个相似日的电价时间序列往往具有较强的关联性。如图4所示，两个相似日96时段电价变化趋势、电价水平都呈现较强的关联性。除历史电价外，负荷变化对电价的影响也较大。导致电价波动的因素如节假日、温度、气候、突发事件等，都已经包含在负荷波动这个主要因素中。

图4 蒙西电力现货市场两个相似日电价对比

在实际电力现货市场中，历史电价与历史负荷也是比较容易获取的数据，因此选择历史电价与历史负荷作为模型的输入变量。

2.2 输入数据的处理

由于蒙西电力市场高载能产业发达、需求弹性相对较大，且新能源装机占比高、外送电量大，故其市场出清电价受新能源出力及外送电量的影响较大。为减少输入变量选择和输入数据处理两个因素对电价预测的影响，将输入数据中的统调负荷、全网新能源出力、外送计划预处理为净负荷，其计算公式见式（3）:

式中：P—净负荷；

L—统调负荷；

E—外送计划；

R—新能源出力。

为了加快模型的训练速度和收敛性，再对输入数据进行归一化处理，将数据映射到[0，1]之间。归一化公式见式（4）：

3 算法实例

3.1 电价预测

选取蒙西电力市场2020-12-01—2020-12-24，2304个时段的日前和实时历史电价及其对应的负荷作为训练样本，预测2020-12-25—2020-12-29，480个时段的市场出清电价，480个时段的日前市场预测电价与实际电价的对比见图5，实时市场预测电价与实际电价的对比见图6，日前市场与实时市场每日的预测误差如表1所示。采用MAPE（平均绝对误差百分比，用M表示）描述预测误差，其计算见公式（5）：

式中：n—样本个数；

—预测电价；

yi—实际电价。

通过图5、图6和表1可以看出，日前市场在12月27日电价有剧烈波动，误差较大，其余时间预测误差在允许范围内；实时市场在12月25日至12月27日出现较多“尖峰”电价，其预测精度有待进一步提高，其余时间预测误差处于允许范围。由于实时市场电价的波动性显著高于日前市场电价，所以实时市场电价的精度并不高。总体来看，SA-BP神经网络模型对日前市场电价预测的效果可以接受，能对蒙西电力市场进行有效预测。

图5 日前电价预测值与实际值对比

图6 实时电价预测值与实际值对比

表1 日前及实时市场MAPE预测结果 %

3.2 误差分析

对相似日平均电价预测法、多项式拟合模型、BP神经网络算法、SA-BP神经网络算法四种方法的预测结果采用MAPE进行误差对比，结果如图7、图8所示。

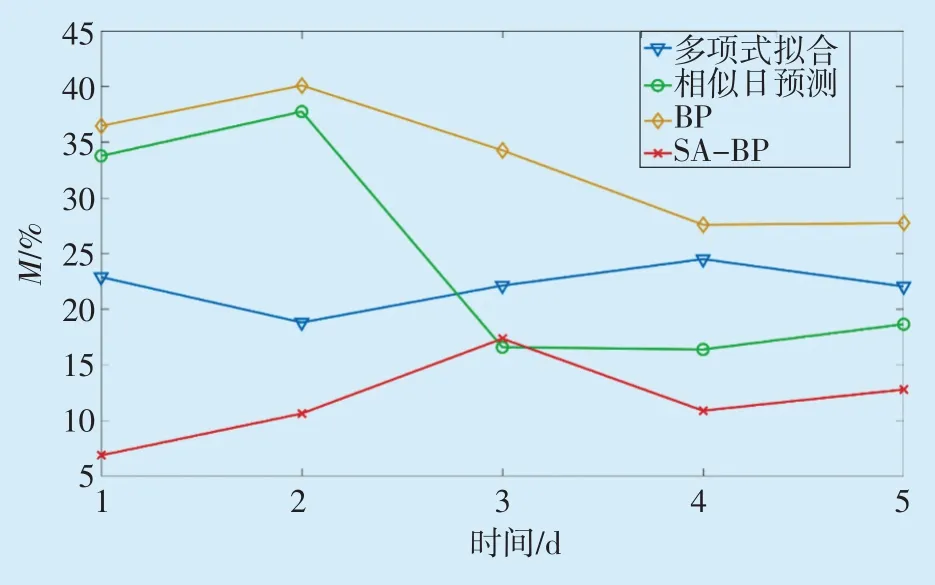
图7 四种方法日前预测电价MAPE对比

从图7、图8可以看出，不论日前市场还是实时市场，SA-BP神经网络模型的预测误差均小于其他三种方法，说明SA-BP神经网络模型电价预测方法比传统方法的预测精度高。

图8 四种方法实时预测电价MAPE对比

4 结束语

考虑影响电价的因素与蒙西电力市场的特点，提出将输入数据预处理为净负荷；针对传统BP神经网络易陷入局部优化的特点，使用梯度下降法与随机扰动机制相结合的方法对BP神经网络进行训练，使其跳出局部优化陷阱。并对蒙西电力现货市场的日前市场电价与实时市场电价进行预测，其预测精度说明该方法适用于蒙西电力现货市场的电价预测。

此算法还可以从以下方面进一步完善：SA算法的参数取值、随机扰动方式、降温方式。参数取值、随机扰动方式、降温方式的多种组合，本文采用传统经验选择，具体哪种选择更为科学有待进一步研究。