基于数据驱动的移动目标卫星任务规划*

温 新，顾 玥

(1.北京航空航天大学 自动化科学与电气工程学院·北京·100191；2.上海航天控制技术研究所·上海·201109)

0 引 言

利用太空卫星观测地面是获取地面信息的重要手段。随着科学技术的发展，军事、经济等领域和各个行业对航空、航天技术的需求不断增加。由于卫星地球观测的范围广，时间性强，并且对地理和国界没有限制，卫星对地球观测的关注和需求已越来越多。

卫星遥感器和地面接收站为卫星地球观测任务提供了极大的便利。与此同时，地面目标的复杂性和对地球观测精度要求的提高也对卫星地球观测任务构成了巨大挑战。因此，如何最大限度地挖掘资源价值，充分利用各种资源获取最大效益，已成为卫星任务规划系统中的一个重要问题。根据遥感观测任务的需求，卫星任务规划需要在约束条件下分配卫星资源和地面站资源。因此，卫星任务规划的目的是为资源分配和活动安排制定最佳的解决方案，使其成为可满足观察需求的最优解。

Mohaed研究了Spot5卫星的日常调度问题，并通过遗传算法直接解决了基本问题。Baek应用了一种新的遗传算法模拟了实际的卫星任务调度问题[1]。上述算法可用于解决实际的卫星任务规划问题，但其主要考虑的是固定地面目标，仍然缺乏对移动目标的观测方法。同时，任务冲突的处理没有与遗传算法进行有效的结合,这导致了算法的效率低下，不利于卫星的任务规划。

本文考虑了用于移动目标观测的卫星任务规划，以克服上述缺点。首先，提出了一种改进的长短期记忆神经网络(Modified Long Short-Term Memory，M-LSTM)移动目标轨迹预测算法，以获取运动目标在未来的信息；随后，利用获得的信息构建了相应的任务规划模型，并设计了约束满足型遗传算法(Constraint Satisfaction Genetic Algorithm，CSGA)，以解决该问题并获得任务规划结果；同时，本文使用了Python环境和STK工具模拟和验证了所设计的算法。

1 M-LSTM轨迹预测算法

移动目标观测需要预测目标的轨迹和位置，这需要从大量的历史轨迹数据中挖掘出潜在的规律。深度学习是近年来流行的人工智能算法，它具有大量的权重矩阵和复杂的参数，可用于拟合大数据之间的对应关系。因此，本文利用深度学习中的长短期记忆神经网络(Long Short-Term Memory，LSTM)算法解决了轨迹预测问题。针对本文研究问题的数据特点，对传统的LSTM算法进行了改进，以适应大量数据的模型。本文主要从两方面进行了改进：动态调整学习率和进行多层次训练，并对传统的LSTM模型结构进行了调整，形成了M-LSTM轨迹预测算法。

1.1 基于LSTM神经网络结构的轨迹预测模型

轨迹预测模型的结构如图1所示。整个航迹预测模型由四部分组成：输入层、LSTM层、Dense层和输出层。输入层是一个简单的输入节点，其主要功能是将运动目标的经度时间序列和纬度时间序列输入到轨迹预测模型中，其内部没有任何运算；LSTM层是整个轨迹预测模型的核心，其包括多层LSTM单元结构。LSTM层包括输入门、输出门和遗忘门，它们的功能是选择或遗忘输入层中的输入时间序列，以达到长时间序列预测的目的；Dense层和输出层是常见的神经网络结构，其主要功能是将轨迹预测结果的特征整合到LSTM层中，并输出轨迹预测结果。

图1 轨迹预测模型Fig.1 The track prediction model

损失函数(也被称为目标函数)由图1中的变量表示。损失函数用于评估轨迹预测模型中预测轨迹序列与实际轨迹序列之间的拟合程度。在求解LSTM算法的过程中，神经网络可通过损失函数不断拟合轨迹预测结果。

在该轨迹预测算法模型中，将运动目标的经度时间序列和纬度时间序列混合在一起进行预测。因此，损失函数可以均方误差的形式进行定义。损失函数可用如下方式表示

(1)

1.2 M-LSTM轨迹预测算法的训练

M-LSTM航迹预测算法训练的主要目的是通过不断更新权重矩阵来提高预测航迹序列与真实航迹序列之间的拟合程度。模型的训练以神经网络中的反向传播思想为基础，拟合程度可根据损失函数的大小进行评定。

M-LSTM轨迹预测算法模型的训练过程主要包括三个部分：前向传播、反向传播和梯度更新。

根据1.1节中的轨迹预测算法模型，输入数据需要被分为训练集和测试集。在执行训练时，轨迹预测模型的输入为训练集中的训练轨迹序列。在第一次正向传播之后，可获得训练集的预测轨道序列。损失函数可用于进行轨迹预测模型的反向传播和梯度更新，由此可以提高训练集中的预测轨迹序列与真实轨迹序列之间的拟合程度。当拟合程度足够好时，将测试集中的轨迹序列代入经过训练的轨迹预测模型，可获得整个算法的最终预测轨迹序列。

(2)

(3)

输入门、遗忘门和输出门的前向计算可以用如下公式表示=

σ

(,)=

σ

(-1++)
=

σ

(,)=

σ

(-1++)
=

σ

(,)

σ

(-1++)

(4)

式中，、、、、、分别是对应的权重矩阵。、、分别表示、、的偏置项。,、,、,分别表示

t

时刻、、的线性输出。

σ

表示激活函数，如下所示

(5)

LSTM层输出轨迹状态的获取需要首先获得LSTM单元的轨迹状态，两者可以表示为

(6)

式中，和-1分别表示

t

和

t

-1时刻的LSTM单位轨迹状态，°表示矢量之间对应元素的相乘。

LSTM层的反向传播过程是误差项沿与时间相反的方向传递的过程。每个参数的误差项的计算如下式所示

(7)

将误差项传递到任意时间

k

的公式如下所示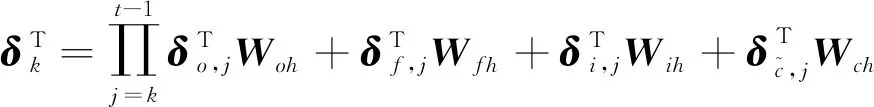

(8)

为了达到轨迹预测的目的，需要不断更新LSTM轨迹预测模型中的权重矩阵，以不断提高预测轨迹序列与真实轨迹序列之间的拟合程度。对于模型中的每个参数，它们的梯度表示每个时刻的梯度之和。梯度更新的计算可以简化为式(9)

(9)

式中，表示的权重矩阵，表示的权重矩阵，表示偏置项。为了提高预测精度，可以采用动态调整学习率的方法。学习率在梯度下降法中即为步长

η

(10)

使用单一的学习率易导致学习率在训练后期相对较大，进而造成准确率抖动，无法获得更优良的预测模型，因此有必要在训练过程中随着训练次数增加而减小学习率。训练初期的损失函数很大，需要更大的学习率以加快训练。训练后期的损失函数变化很小，需要使用更小的学习率，以防止准确率来回抖动。经过实验验证，本文采用的等距下降法可对学习率进行调整，得到的预测效果最佳。等距下降法的具体方法为：每经过50轮的学习步长，学习率减小至上一轮的50%。

同样地，为了提高预测精度，可采用多层次训练的方法。将搭建好的神经网络模型反复训练3次，每次训练时将由上一次模型训练而得到的最佳权值矩阵加以保存，重新设置模型初始学习率，并将其加载到新的模型中进行训练。由于加载了之前训练结果的优良特征，就不需要从零开始训练神经网络。采用这种学习方法，不需要在短时间内修改过多的权重，只需进行微调便可获得更为精确的学习模型，从而提高预测的准确率。

2 CSGA任务规划算法

2.1 CSGA任务规划算法的模型

(1)任务描述

在获得移动目标的预测轨迹之后，卫星任务规划可以描述为：在遥感设备(资源集合

M

)数量有限的前提下，在指定的时间内安排了

n

个点的目标观测任务的执行方案。

移动目标卫星观测具有时间跨度大、观测持续时间短、观测次数少的特点。由于资源能力、用户要求和调度时间的限制，所有可见时间窗口有可能未被完全安排。每个可见时间窗口都有其相应的权重，表示该可见时间窗口中观测任务完成时的可用收益。如果不能完全安排所有可见时间窗口，则必须生成总收益较大的方案。

最佳的任务规划方案应满足以下条件：

1)每一个活动只能在自己的满足约束条件的时间窗口内被执行；否则，认为该活动未被执行；

2)每一个活动执行只能占用满足其要求的资源中的一个资源，且执行过程不能被中断；

3)每一个资源在任何时候都只能同时执行一个活动；

4)所安排执行的活动的总权值最大。

(2)约束条件描述

根据第(1)节中的任务描述，移动目标观测的卫星任务规划需要满足以下约束：

1)可见性约束

由于移动目标的观测特性，所有卫星观测活动都需要在卫星与移动目标之间的可见时间窗口内被执行，并且要执行的观测任务必须在初始任务序列中。公式表示如下

task

∈{

w

,

w

,…,

w

}

(11)

式中，

task

表示要执行的观测任务，

n

表示观测时间窗口的编号，

w

表示初始任务序列中的第

i

个可见时间窗口，

w

可以用下式描述

w

={[

wb

,

wf

],

target

}

(12)

式中，

wb

和

wf

分别是该可见时间窗口的开始时间和结束时间，

target

表示第

k

个移动目标的信息。

2)可见时间窗口的时间约束

考虑到有效载荷的使用约束条件和卫星平台约束条件，只有持续时间大于

T

分钟的可见时间窗口才能被视为有效可见时间窗口。此约束可由以下公式描述|

wf

-

wb

|≥

T

(13)

3)卫星传感器约束

卫星只有一个观察传感器。该卫星只能执行侧摆和俯仰机动，并且在一个时间段内只能观察到一个有效目标。该约束可以由下式描述

(14)

4)观测任务次数约束

考虑到任务要求和卫星执行能力，观察任务的数量存在最大数目限制。该约束可由下式描述

tasknum

≤

task

_

size

(15)

式中，

tasknum

表示已执行任务的总数，

task

_

size

表示观察任务的最大数量。

(3)目标函数

最优化规划的目标函数可以根据任务要求给出。根据以上描述，移动目标观测任务规划的目标是该方案的总收益最大化。因此，目标函数可由下式表示

(16)

s.t.|

wf

-

wb

|≥

T

(17)

tasknum

≤

task

_

size

(18)

(19)

式中，

F

(

X

)表示任务规划方案

X

的总收益值。

c

(

w

)表示可见时间窗口

w

的权重。

u

(

w

)表示

w

在该方案中是否被执行，

u

(

w

)可由下式表示

(20)

2.2 CSGA任务规划算法

根据上一节描述的移动目标卫星任务规划模型，需要根据模型的特征设计相应的任务计划算法。遗传算法当前被广泛应用于各个领域，并且很适合解决这类优化问题。由于任务的复杂性，需要对传统的遗传算法进行改进，以满足与移动目标观测相对应的约束和冲突任务处理问题，从而可以获得最优解。主要的改进为设计及加入了冲突消除算子，并设计了相应的选择算子。

(1)编码方式

DNA编码是遗传算法需要首先解决的问题。由于仅存在被执行或未被执行两种任务观测状态，因此最终期望的任务规划方案是与时间序列相关的执行序列。本文结合上一节所提到的目标函数，以可见时间窗口为单位对初始任务序列进行了编码，编码结构如图2所示

图2 DNA编码结构Fig.2 The DNA encoding structure

(2)适应度函数

适应度函数可用于评估个体的收益值，以指导遗传算法中的对优良个体的选择。根据第(1)节所述的目标函数，适应度函数可以表示为下式

(21)

式中，

pop

表示种群中的第

j

个个体。

(3)种群初始化

采用随机生成方法初始化种群。每个DNA都是在DNA长度相同且种群大小恒定的条件下随机产生的，种群大小为

pop

_

size

。

(4)冲突消除算子

根据第(1)节描述的移动目标卫星任务规划模型，每种资源一次只能执行一项观察活动。因此，由于时间窗口存在冲突，有些任务无法同时被完成。如果最终个体在DNA中的基因位置上存在时间冲突，则该个体是不可行的方案。因此，必须消除个体冲突的基因位，并获得尽可能无冲突的最终可行方案。结合移动目标卫星观测的特点，专门设计了冲突消除算子来处理时间窗口冲突，以提高效率和得到最终可行的求解结果。将冲突消除算子的结果嵌入选择算子中，判断时间窗口是否存在冲突的标准如下所示

wf

≥

wb

≥

wb

or

wf

≥

wf

≥

wb

(22)

冲突消除算子可以表示为伪代码1中所示的伪代码

伪代码1:冲突消除算子Input: The initial task sequence X={w1,w2,…,wn}Output: Conflict task sequence C= {(m1,n1),(m2,n2),…,(mk,nk)}1: function conflict (n, X)2: C=Ø3: for i in (1,2,…,n):4: for j in (1,2,…,n):5: if wfj≥wbi≥wbj:6: C add (wi,wj);7: else if wfj≥wfi≥wbj:8: C add (wi,wj);9: for every (wi,wj) in C:10: check for duplicate combinations of (wi,wj) in C;11: delete duplicate;12: return C

(5)选择算子

选择算子从整个种群中选择更好的个体，并将其保留到下一代，这些个体用于指导整个种群的进化方向。本文采用轮盘赌选择法，每个个体被选中的概率与其适应度函数的值呈正比。选择函数可以表示为

(23)

式中，

P

(

pop

)表示个体

pop

被选中的概率。

为了满足移动目标卫星观测的特点和约束，本文设计了一种独特的选择算子。可在选择算子中执行约束计算和处理，并在该算子中导入冲突消除算子的计算结果以处理冲突。由此，可以准确地选择满足约束条件且无冲突的个体。

选择算子可以表示为伪代码2中所示的伪代码。

(6)遗传算子

遗传算子基本采用传统遗传算法进行操作，交叉算子使用在任务级别的单点交叉点。将交叉概率设置为

α

，只有满足交叉概率的个体才能进行交叉操作。变异算子使用基本位置变异法。设定变异概率为

β

，并对满足变异概率的单个基因位置进行变异操作。DNA复制采用了两代竞争法。每次生成子代个体时，都要比较子代和父代个体之间的适应度函数值，更为优秀的个体将被保留在种群中。

伪代码2:选择算子Input: Population pop, The maximum tasks number task_size, The minimum observation time Tmin, Conflict task sequence C, Fitness function F(x)Output: The new population pop_new1: function selection (pop,task_size, Tmin,F(x),C)2: for i in (1,2,…,pop_size):3: for j in (1,2,…,n):4: if wfpopij-wbpopijtask_size:9: P(popi)=0;10: else:11: for j in (1,2,…,n):12: if u(wj)=1:13: if wj in C:14: check conflict task wc of wj:15: if u(wc)=1:16: P(popi)=1;17: select pop_new in pop with {P(pop1),P(pop2),…,P(poppop_size)};18: return pop_new

3 仿真试验及结果分析

3.1 仿真环境

仿真是在Python环境中采用STK工具执行的。本文定义了具有三种移动目标的场景，以测试本文提出的算法的效率。该场景开始于2016.01.01.00:00:00，结束于2016.12.31.23:59:59，仿真参数如表1、表2、表3和表4所示。卫星俯仰角范围为-60°～60°，卫星侧摆角范围为-20°～20°。当卫星位于被观测目标上方且被观测目标的太阳高度角大于5°时，卫星处于可观测时间。

表1 移动目标参数Tab.1 Moving targets information

表2 M-LSTM算法参数Tab.2 M-LSTM algorithm parameters

表3 CSGA算法参数Tab.3 CSGA algorithm parameters

表4 卫星参数Tab.4 The satellite parameters

3.2 仿真结果

仿真结果包含了M-LSTM轨迹预测结果和CSGA任务规划结果。

(1)轨迹预测结果

轨迹预测结果和轨迹预测误差如图3、图4所示。

图3 轨迹预测结果Fig.3 The track prediction results

(a)采用M-LSTM算法的仿真结果

图3展示了STK中的所有轨迹预测结果。图4为用等步长采样法对所有三种目标进行的轨迹预测误差，图4(a)为采用M-LSTM算法的仿真结果，图4(b)为采用普通LSTM算法的仿真结果。图4(a)显示，大多数轨迹点的误差值都在40km之内。经计算，当卫星观测拍摄视场的半径为40 km时，图4(a)中每个目标的预测精度如下：目标A为86.8%，目标B为94.5%，目标C为94.0%，整体精度为91.9%。图4(b)显示，轨迹点的误差值分布较为分散，误差较大的点众多。经计算，当卫星观测拍摄视场的半径为40 km时，图4(b)中每个目标的预测精度如下：目标A为56.3%，目标B为67.6%，目标C为63.5%，整体精度为62.8%。当卫星在图4中的采样点时刻观测船只目标时，只要预测点与真实目标位置的距离在40km之内，卫星按照预测点对目标进行观测，就可以在观测视场内拍摄到预期目标，这样就完成了对目标的观测，表示预测成功。通过对比仿真可以看出，M-LSTM算法较普通LSTM算法在很大程度上提升了算法精度，达到了预期效果。由于目前大多数观测卫星的拍摄视场半径都达到了40km，由此可见预测效果非常出色。

(2)任务规划结果

在获得了第(1)节所述的移动目标轨迹预测结果后，移动目标任务规划的部分结果如表5所示。

表5 任务规划结果(部分)Tab.5 Mission planning results (partial)

任务规划的仿真结果如表5所示，该方案的适应度函数值为4096。根据此模型计算得出的最大适应度函数值为4240，因此收益百分比为96.6%。经过对比仿真，在此场景下应用普通遗传算法进行求解存在大量冲突时间窗口，观测数目也不满足要求，收益百分比普遍低于50%。由此可见，CSGA算法的效果更加优良。

由于求解过程具备不确定性和波动性，可采用多次仿真取平均值的方法获得更加准确的结果。本文进行了100次蒙特卡洛仿真实验，基本参数如表4所示，结果如图5所示。

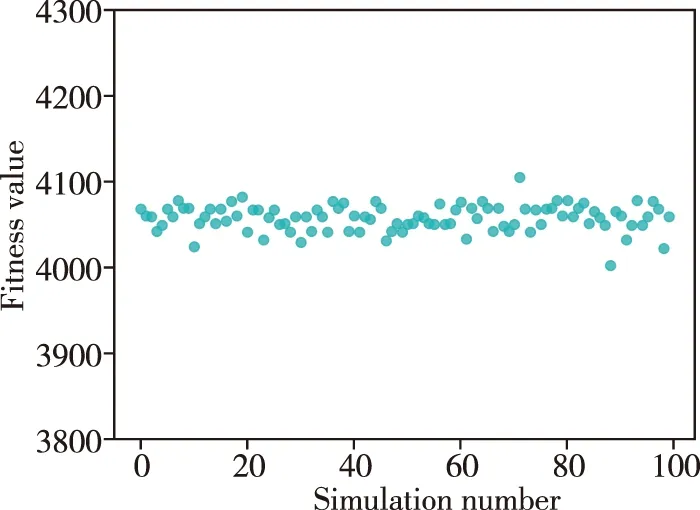
图5 蒙特卡洛仿真实验结果Fig.5 Monte Carlo simulation experiments results

如图5所示，100次实验结果的适应度函数值主要集中在4000～4100，平均值为4057.59。因此，收益百分比已达到95.7%。仿真结果表明，该算法可以很好地解决该问题。

4 结 论

本文提出了将M-LSTM算法和CSGA算法进行结合来实现移动目标观测的卫星任务规划的可行方案，所提出的算法解决了预测移动目标信息以及卫星观测任务规划的问题。仿真结果表明，M-LSTM算法可预测出较好的结果、误差较小，而CSGA算法适用于任务计划且收益率很高。综上所述，本文提出的模型和算法具有较强的实际应用价值。