基于MATLAB的系统稳定性分析的演示程序设计

燕丽鸽，孙园志，王志鹏（通讯作者）

（南阳师范学院物理与电子工程学院 河南 南阳 473061）

1 引言

系统若要实现其自身的功能，必须具有稳定系统。若一个系统的输入是有界的且输出也是有界的则该系统为稳定系统。若系统不是稳定系统，其输出无界，此时系统为非线性系统；设备无法承受极大的输出，进而系统不仅不能处于我们所需的工作状态，也可能会损毁设备[1]。因而，事先判断系统是否稳定就格外重要。判断系统是否稳定的方法有很多，在控制理论中，判断系统是否为稳定系统的判据为传递函数的极点在复平面左边。

利用经典传统方法判断一个系统的稳定性，是复杂且繁琐的，且难以达到证明目的。其一是因为计算量太大，难以高效进行；其二是传统方法无法得到强信服力的图形来支撑观点加以论证。若是人工计算，可能只是判断是否稳定，而不能准确地画出直观的图形以及得到一些准确的数据。所以，人们提出很多辅助方法来帮助判断系统稳定性，例如劳斯判据、绘制根轨迹、波特图等[2]。在控制系统稳定性时，由于精准数值的要求使解得该系统的阶跃响应是困难的，且难以描绘精确直观的频率响应曲线，所以便可借助电脑软件MATLAB进行计算以及描绘曲线，同时也可以对系统性能有某些影响的参数进行研究[3]。

此外，MATLAB该软件实验界面友好，操作很简单，图形界面设计一目了然，所占内存小，容易上手使用，还可用于系统分析和系统设计的教学实验。在MATLAB的GUI窗口图形界面可以自主设计，通过设计界面、调用函数完成演示。通过观察GUI演示界面可以简单、快速、直观、有效地判断一个系统是否稳定。在MATLAB软件中，其函数库提供了大量的数学公式，可省去人工计算，大大减少误差，并且极大地方便进行各种计算及描绘图形；库中还包含有图形绘制的函数，这样便得到足以支撑论证且精确的图形，使得经典控制中判断系统稳定性变得简单[4]。

2 演示程序的总体结构

根据《信号与系统》课程的一些知识，若一个连续或离散系统是有界输入有界输出，那么该系统是稳定的。在众多的经典系统中，可以通过多种方法来判断一个系统是否稳定[1]，在本文中选取了零极点图[5]、根轨迹法、波特图[6]这3种方法来进行演示。该演示程序设计的总体结构框图见图1，点击每一个按钮，都可以分别打开不同的系统稳定性分析子模块。

图1 演示程序设计的主页面图

3 子模块介绍

3.1 零极点图

在一个线性是不变系统中，若系统的传递函数H（s），其所求解的所有极点均位于复平面的左半平面内，出现在时域响应e的指数部分，因为传递函数极点的实部都小于0，伴随着时间函数的逐渐变大，其结果会逐渐趋于0，因此该系统是稳定的。对应在时域中，极点的实部小于0，是个振荡衰减的函数，最后一定会稳定。

在离散系统中，在求解其所对应的系统函数H（z）后，其收敛域包含单位圆，则该系统是稳定系统；若对系统输入任意有界的序列，系统输出也是有界的，那么该系统是稳定的。

演示程序设计的零极点图图形界面见图2。

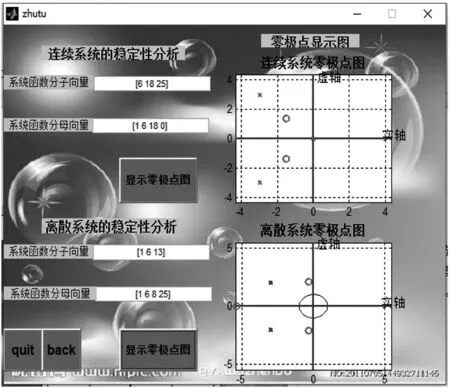
图2 演示程序设计的零极点图图形界面

该GUI程序可以通过在动态文本框里输入系统函数的分子、分母向量后，点击对应按键，可以分别对应显示连续、离散系统的零极点图显示在坐标轴上，通过点击back按键，可以返回到主界面，若不再进行演示，通过点击quit按键退出GUI程序演示界面。

利用零极点图判断连续系统稳定性的回调函数如下：

axes(handles.axes1)；

a1=handles.axes1；

cla(a1)；

plot([-x x]，[0 0]，'b-'，'LineWidth'，2)；

hold on；

plot([0 0]，[-y y]，'b-'，'LineWidth'，2)；

plot(real(p)，imag(p)，'rx'，'LineWidth'，2)；

plot(real(q)，imag(q)，'ro'，'LineWidth'，2)；

利用零极点图判断离散系统稳定性的回调函数如下：

axes(handles.axes2)；

a2=handles.axes2；

cla(a2)；

hold on；

w=0:pi/200:2*pi；

b=exp(i*w)；

plot(b)；

plot([-x x]，[0 0]，'LineWidth'，1.5)；

plot([0 0]，[-y y]，'LineWidth'，1.5)；

plot(real(p)，imag(p)，'rx'，'LineWidth'，2)；

plot(real(q)，imag(q)，'ro'，'LineWidth'，2)；

3.2 根轨迹法

绘制根轨迹的主要思路就是根据其特征方程的性质与零极点和参数的关系，总结根轨迹的规律便可画出根轨迹图和变化趋势。继前言，描制图形依然可用MATLAB绘出；在其函数库中，直接提供了求取函数零极点的函数以及绘制根轨迹的函数（rlocus、rlocfind、pzmap等），所以我们可以根据所绘制的零极点图在平面的分布情况直接判断该系统是否稳定[2]。

演示程序设计的根轨迹法图形界面见图3。

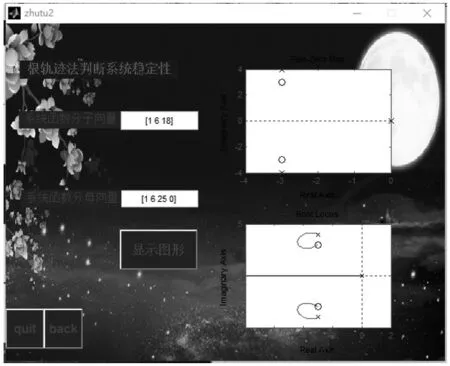
图3 演示程序设计的零极点图图形界面

该GUI程序可以通过在动态文本框里输入系统函数的分子、分母向量后，点击显示图形按键，可以在两个坐标轴上显示零极点图和根轨迹图，通过点击back按键，可以返回到主界面，若不再进行演示，通过点击quit按键退出GUI程序演示界面。

根轨迹法的回调函数：

g=tf(A，B)；

axes(handles.axes2)；

ax_2=handles.axes2；

cla(ax_2)；

hold on；

rlocus(g)；

axes(handles.axes1)；

ax_1=handles.axes1；

cla(ax_1)；

hold on；

pzmap(g)；

3.3 波特图

波特图又称对数频率特性曲线，波特图是线性系统的传递函数对频率的半对数坐标图。利用波特图可以观察系统的频率响应，包括幅频响应和相频响应曲线图[2]。利用波特图进行稳定性判定的依据是：幅值裕度GM＞0且相角PM裕度＞0，但是使用该判据进行稳定性判定必须满足一个前提条件：系统的开环传递函数必须为最小相位系统。

演示程序设计的波特图图形界面见图4。

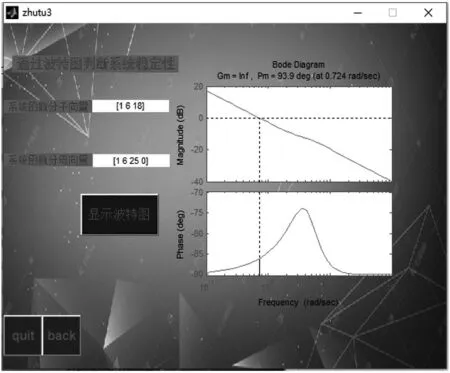
图4 演示程序设计的零极点图图形界面

该GUI程序可以通过在动态文本框里输入系统函数的分子、分母向量后，点击显示波特图按键，可以显示出该系统的波特图以及频率图，通过点击back按键，可以返回到主界面，若不再进行演示，通过点击quit按键退出GUI程序演示界面。

波特图的回调函数：

g=tf(A，B)；

axes(handles.axes1)；

ax_1=handles.axes1；

cla(ax_1)；

hold on；

bode(g)；

margin(g)；

4 结语

本文采用了计算机 MATLAB软件，通过GUI窗口设计，调用函数的方法进行系统稳定性的判断。采用了系统的开环传递函数，求解其函数特征方程的零、极点、闭环特征根，在时域、频域中绘制图形，对系统稳定性进行判别研究。设计了零极点、根轨迹、波特图的GUI界面，可以实现对系统稳定性的判定，具有操作简单、显示直观、易懂、精准的优点，避免了传统方法的繁琐、不准确以及一些误差，更便于使用。在此过程中，既避免了繁琐的分析计算过程，极大地提高了可信度，又可通过计算机绘制图形，得到有信服力的图形来支持论证，让结果更加严谨，且拥有更高的真实性[7]。亦可实现投入课堂讲学的使用，通过实际的操作让学生们更好地理解相关知识，提升课堂效率和提高课堂质量。