乡村振兴战略下我国乡村旅游PPP项目激励约束机制研究
王金萍,刘宗飞,赵伟峰
(安徽科技学院管理学院,滁州 233100)
乡村旅游是乡村振兴战略的重要抓手。近年来,中央部门和地方政府紧密围绕实施乡村振兴战略,聚焦全国乡村旅游的开发和建设,促进乡村旅游产业提质升级,陆续出台了一系列重要纲领性文件,助推乡村旅游的高质量发展。2019年,《国务院关于促进乡村产业振兴的指导意见》提出要优化乡村休闲旅游业,培育多元融合主体;《关于金融支持全国乡村旅游重点村建设的通知》进一步提出要鼓励和引导民间投资通过PPP、公建民营、政府增信、产业基金等方式参与乡村旅游基础设施建设和运营。PPP(Public-Private-Partnership)即政府与社会资本合作,通过优势互补、风险共担、利益共享,引导社会资本参与公共服务或产品的供给,彼此形成的一种伙伴合作关系[1-2]。PPP模式作为一种优化的投融资模式,以实现各参与方“双赢”或“多赢”为合作理念,充分发挥政府和社会资本的优势。在乡村旅游中引入PPP模式可以有效解决长期以来乡村旅游开发中资金困乏、村民运营乡村旅游项目专业性不足等问题,推动乡村旅游的可持续发展[3]。
1 委托代理理论概述
经典的委托代理理论在20世纪30年代由美国经济学家伯利和米恩斯提出,认为现代公司的发展出现了“所有权和经营权”两权分离的现象[4]。委托代理关系便是随着所有权和经营权的逐渐分离而产生的。杰森和麦克林认为委托代理关系是一种契约,一个或多个行为主体指定另一个行为主体为其提供服务,并根据提供服务的数量和质量给予相应的报酬,委托方是委托人,被委托方为代理人[5]。委托代理理论建立在非对称信息博弈论的基础上,强调委托人和代理人信息不对称和利益不一致,是制度经济学契约理论的主要内容之一[6]。PPP模式下,政府和社会资本通过签订契约,委托社会资本参与公共服务或产品的供给,形成委托代理关系,政府是委托人,社会资本是代理人[7]。在乡村旅游PPP项目中,政府和社会资本目标函数不一致,政府较为关注社会效益,而社会资本更为关注经济效益,且二者之间信息不对称,政府拥有更多的信息资源,但政府不容易观察到社会资本工作的努力程度,目标的不一致及信息的不对称容易引起机会主义行为[8]。在信息不对称前提下,社会资本作为理性经纪人,以最大化自身利益为目标而忽略项目整体利益,政府不能直接观测到社会资本的行动,只能通过其行动结果片面评价社会资本是否尽最大努力工作[9]。建立有效的激励与约束机制可以限制社会资本在乡村旅游PPP项目中的投机行为,在保障社会资本基本利益的同时实现社会公共福利最大化。
2 不对称信息下模型构建
2.1 模型假设

假设2:假定签订特许经营合同时规定基础收益标准为X0,政府将根据乡村旅游PPP项目最终收益支付社会资本报酬,支付给社会资本的固定报酬设为W,当x>X0时,政府将会激励社会资本的付出,超额收益激励系数用β表示。乡村旅游PPP项目采用线性合同,社会资本收益函数设为S(x)=W+β(x-X0)。
假设3:乡村旅游PPP项目中政府的使命是为了社会福利最大化而努力,面对风险时表现为风险中性,社会资本竭尽全力保证自身利益最大化,面对不确定性时表现为风险规避,效用函数为U(x)=-e-ρx,其中ρ衡量绝对风险规避程度,x是实际货币收入[10]。
假设4:假定乡村旅游PPP项目政府监督成本函数为M(p)=mp2,其中m是监督工作成本系数,m值越大,政府监督成本越大;p是监督水平,即政府部门能发现社会资本达不到合同要求的概率,p值越大,监督成本也越大。若社会资本达不到合同约定质量、安全、环保等标准,将给予处罚(X0-x)F0,F0为政府对社会资本的处罚系数,则处罚期望函数表示为E(F)=E[p*(X0-x)F0+(1-p)*0)]=pF0(X0-x)。
2.2 激励模型构建
假定在不对称信息下的激励模型中政府较为容易观察到社会资本努力程度及努力效果,观测成本较低,不需要约束社会资本,政府监督成本为0,不引入M(p)及F(x)。
2.2.1 政府部门收益函数 由假设3,政府部门风险中性,政府部门收益等于乡村旅游PPP项目总收益扣除支付给社会资本的报酬,收益函数表达式g1:
g1=x-S(x)=x-[W+β1(x-X0)]=(1-β1)(a∂1+ε)-W+β1X0
(1)
政府部门的期望效用函数等价于其确定性收益,即:
E(g1)=E[(1-β1)(a∂1+ε)-W+β1X0]=(1-β1)a∂1-W+β1X0
(2)

(3)
社会资本的期望效用函数等价于其确定性收益,即:
(4)

(5)
除了满足社会资本的最低保留效用之外,在信息不对称和自利的情况下政府只能在一定程度上观测到社会资本的努力程度∂1,社会资本出于自身利益的考虑,会选择使自身效用最大化的努力水平。
对社会资本的期望效用函数求∂1的偏导数:
老大妈推着婴儿车走了,突然,苏母问他:婷婷是不是也快生了?苏穆武不解地:生什么?苏母说:外孙呀!结婚前她不是说怀孕了吗?苏穆武恍然地:我把这档子事差点忘了。苏母沉吟地:奇怪,怎么一点看不出来呢?
(6)
在满足约束条件(I.R)和(I.C)的前提下,政府的期望是使其效用最大化,即max[(1-β1)a∂1-W+β1X0]
(7)
构建拉格朗日函数L1(β1,λ1),政府部门期望效用的最大化等价于求L1(β1,λ1)的最大值,构建函数:
(8)
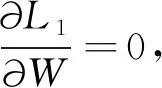

(9)
2.3 激励-监督模型构建
不对称信息下的激励-监督模型假定政府较为不易观察社会资本努力程度及努力效果,观测成本较高,激励-监督模型相比激励模型引入了政府监督成本函数M(p)及F(x),两种模型的强调重点不同,监督模型政府需要花费更多的心思约束社会资本,而激励模型则要花费很多的报酬激发社会资本的积极性。
2.3.1 政府部门收益函数 由假设3,政府部门风险中性,政府部门收益等于乡村旅游PPP项目总收益扣除支付给社会资本的报酬S(x)、政府监督工作成本M(p)再加上发现社会资本努力成果不符合合同约定时的处罚金额F(x),收益函数表达式g2:
g2=x-S(x)+F(x)-M(p)=(1-β2-pF0)(a∂2+ε)-W+β2X0+pF0X0-mp2
(10)
E(g2)=(1-β2-pF0)a∂2-W+β2X0+pF0X0-mp2
(11)
2.3.2 社会资本收益函数 此处社会资本净收益考虑了社会资本行为不符合合同约定时被处罚金函数F(x),收益函数表达式p2:
(12)
此种情况下,社会资本的期望效用函数为:
(13)
此模式下政府效用函数的最大化同样也受到激励相容约束和参与约束条件的影响。同理,对社会资本的期望效用函数求∂的偏导数:
(14)
在满足约束条件(I.R)和(I.C)的前提下,政府的期望是让其效用最大化,即:
max[(1-β2-pF0)a∂2-W+β2X0+pF0X0-mp2]
(15)
构建拉格朗日函数L2(β2,λ2),政府效用最大化等价于求L2(β2,λ2)最大值:
L2(β2,λ2)=(1-β2-pF0)a∂2-W+β2X0+pF0X0-mp2
(16)

(17)
(18)
3 模型求解结果分析
3.1 社会资本的努力水平
3.2 合同设置的激励系数
3.3 社会资本的风险感知度

3.4 政府部门的监督强度
4 小 结
乡村旅游开发中引入PPP模式较好地缓解了美丽乡村建设中的资金不足,提高乡村旅游产品或服务的供给效率,减轻了政府的财政压力。在乡村旅游PPP项目中建立有效的激励机制可以激发社会资本努力工作,而将激励策略与约束策略结合则更大程度地激发社会资本的努力水平,两者形成合力,保证美丽乡村开发建设的顺利推进。在委托代理基础之上,综合考虑政府和社会资本信息不对称的情况,构建不对称信息下的激励模型与激励-监督模型,深入探讨了多元参数影响下两种模式的社会资本最优努力水平及最佳激励系数。结果表明,两种模式的社会资本努力水平、合同设置的激励系数、社会资本风险感知度以及政府部门的监督强度方面均存在差异。激励模式下的社会资本努力供给小于激励-监督模型下的社会资本努力供给,两种模式下激励系数的数量关系则相反。另外,当风险感知度逐渐增高时,社会资本会降低努力水平以尽可能规避风险,政府应适当降低对社会资本的激励系数,反向促进社会资本积极工作;当政府耗费较多的资源实施监督工作、发现社会资本不利行为处罚力度较高时,社会资本工作积极性较高;政府开展监督工作所花费成本越高时,政府的监督积极性大打折扣,社会资本努力成本越高时,滋生消极工作情绪,政府更需加强监督力度。在乡村旅游PPP项目中激励机制与约束机制不是对立面,而是应该站在同一条战线,加强协作,共同推进PPP模式在乡村旅游开发中的作用,为实现乡村振兴助力。

