基于模糊数学的高维稀疏数据聚类统计方法设计
周燕茹
(巢湖学院 数学与统计学院,安徽 巢湖 238000)
随着数据库管理系统的应用范围越来越广,企业或其他机构均积攒了海量数据[1].对数据实施聚类统计处理能够判断数据间的相似度,从而获取重要的数据特征信息.然而,数据维度与稀疏度成反比,数据对象会分布于各个维度子空间内,传统的聚类方法在这方面的聚类效果较差,原因是距离函数容易无效、算法复杂度高与聚类中心选择过于随机等[2-3].且传统的数据分析工具仅具备查询与统计等作用,难以高效聚类高维稀疏数据.
一直以来,高维稀疏数据聚类统计方法始终是数据挖掘方面的一大难题[4].邵俊健[5]等人针对高维数据聚类效果较差问题,设计了一种具有抗噪性能适用高维数据的增量式聚类统计方法,提升其抗噪性能与聚类效果;武森[6]等人针对数据对象易于划分至更大类内问题,设计了一种基于拓展差异度的高维数据聚类统计方法,有效缩短聚类时间.然而在实际应用中发现,随着现阶段数据量及其复杂度的提高,上述两种方法在聚类统计稀疏度较低的数据集时效果仍然较差.
模糊数学是一种分析模糊性情况的数学方法,主要用于模糊聚类分析与模糊综合评判等.其中,最为常用的是模糊C均值算法(Fuzzy C-means,FCM).为此,本研究以FCM算法为基础,设计了基于模糊数学的高维稀疏数据聚类统计方法,以期提升聚类统计效果.
1 高维稀疏数据聚类统计方法设计
1.1 FCM算法
FCM算法是模糊数学的分支,该算法以模糊思想表示对象和簇间的关系.对象y对于集合A的模糊隶属度函数是hA(y),hA(y)∈[0,1],在数据聚类过程中,将聚类获取的簇当作模糊集合,FCM算法目标函数的表达公式如下:
(1)
其中,聚类中心编号为i;数据点编号为j;模糊组的聚类中心为ci;hij∈[0,1];加权指数为m∈(1,∞);i与j之间的欧几里德距离为dij=‖yj-ci‖2.
FCM算法的具体处理步骤如下:
步骤1:获取聚类数量c(2≤c≤n),样本数量为n,确定m(2≤m≤∞)的值;初始化隶属矩阵H得到H(T),将T作为迭代的标记.初始化需要符合的要求如下:
(2)
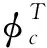
(3)
(4)
其中,聚类中心编号是k.
步骤4:对比分析每次优化后隶属矩阵的差距,若‖H(T+1)-H(T)‖<εT,那么完成聚类统计,隶属矩阵差距的标准数值是εr;若‖H(T+1)-H(T)‖>εT,设置T=T+1,返回至步骤2.
1.2 改进的模糊聚类算法与聚类统计方法设计
1.2.1 优化初始聚类中心
为避免陷入局部最优,在FCM算法运算过程中,需要反复初始化聚类中心,延长聚类统计时间.为解决这一问题,本研究利用特殊的初始聚类中心选取方法,获取数据集凸包边界中的初始聚类中心,确保各聚类中心距离较远,避免出现局部最小值的情况.具体步骤如下:
步骤1:求解数据集的平均值,将与该值距离最远的数据点当成首簇聚类中心;
步骤2:计算首簇聚类中心与全部数据点间的距离;
步骤3:按照贪心选择策略选取首簇聚类中心以及平均值较远的数据点,将其当成第二簇聚类中心,直到得到k簇聚类中心为止;
步骤4:以平均值为目标,令全部聚类中心向其移动,移动间距为两者距离的10%,提升聚类的收敛速度[7].
1.2.2 类间中心点影响
由于FCM算法并未分析各类别数据簇中心点间的彼此排斥影响,导致该算法难以对高维稀疏数据实施聚类,通过添加权重机制[8]改进FCM算法,使其适用于高维稀疏数据的聚类统计.将已知类与未知类均添加至FCM的目标函数内,变更后的目标函数为:
(5)
其中,未知类内第i簇聚类中心为Pi;已知类内第k簇聚类中心为Rk;权重为wj;第j个数据点包含在i内的程度为αij;j包含在k内的程度为βkj;聚类中心数量为l.α与β需符合的条件如下:
(6)
通过拉格朗日乘子法计算:
(7)
其中,拉格朗日乘法算子为λ.
计算G(H,T,P,λ)内变量Pi的偏导,过程如下:
(8)
根据公式(8)可得到:
(9)
依据同样方法求解G(H,T,P,λ)内变量αij与βkj的偏导,公式如下:
(10)
(11)
其中,簇的编号分别为a与b.
通过引入权重机制提升FCM算法中各类簇的聚类中心竞争剩余数据点间重叠范围内的特征空间.通过加权指数m决定簇心间的排斥力,该值与排斥力成正比[9].
1.2.3 优化余弦距离
虽然FCM算法具备较优的聚类低维数据集性能,但在聚类高维稀疏数据时,其效果不佳[10].由余弦距离替换FCM算法中的欧几里德距离,计算公式如下:
(12)
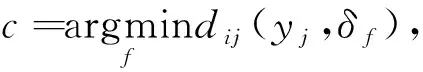
(13)
根据公式(13)可得到:
(14)
在每个数据块很小(对象很少)的情况下,为各簇划分的对象数量同样较少[11],说明χc也较小.针对各簇仅存在一个对象的现象,获取:
(15)
其中,高维稀疏数据向量为yj,该向量中仅包含非常少的非零元素.这就说明yj和剩余数据间常用词的数量明显低于各数据内存在的词数量[12].通过二进制方法加权内yj的词,若yj内存在单词,那么yji=1;若yj内不存在单词,那么xji=0,针对这一情况可获取:
(16)
得到:
(17)
在高维稀疏数据内数据块不大的情况下,通过‖φc‖2确定d(xj,φc).同时,由于‖φc‖2的值与yj没有关系,为避免全部对象划分到和聚类中心存在最小欧几里德距离的相同簇内,在各次迭代结束时[13],需标准化处理聚类中心,公式如下:
(18)
标准化处理聚类中心时,对象与聚类中心的距离通过公式(12)右侧的最后一项确定,它属于yj与φc间的内积,确保FCM算法中的h存在意义,针对FCM算法存在:
(19)
更改上述公式获取:
(20)

(21)
为解决模糊聚类内yj在全部簇内的隶属度非常接近问题,需要归一化处理各目标矢量[15],使其变成单位范数‖yj‖=1.欧几里德距离公式变更为:
(22)
在yj归一化成单位长度的情况下,FCM算法的全部迭代过程中,优化完成的聚类中心归一化已改为基于余弦距离的FCM算法.基于此,以余弦距离替换原有的欧几里德距离,提高高维稀疏数据聚类统计效果.由此,通过优化模糊数学中的FCM算法实现了对高维稀疏数据的聚类统计.
2 实验与分析
2.1 实验设置
为验证上述设计的基于模糊数学的高维稀疏数据聚类统计方法的实际应用性能,设计如下实验.将文献[5]中的具有抗噪性能适用高维数据的增量式聚类统计方法(方法1)和文献[6]中的基于拓展差异度的高维数据聚类统计方法(方法2)作为对比,要个具体点的方向本文方法共同完成性能验证.
将HR(Hit-rate,命中率)与ARI(Adjusted Rand Index,调整兰德指数)作为衡量3种方法聚类统计性能的指标,HR的取值范围是[0,0.3],ARI的取值范围是[0,1],两者的取值均与聚类效果成正比.其中,HR的取值高于0.2则代表该方法具备较优的聚类效果,ARI的取值高于0.5则代表该方法具备较优的聚类效果.
在某网络中随机选取6个真实数据集作为实验对象,数据集的具体信息如表1所示.

表1 数据集的具体信息
2.2 性能分析
为确保3种方法具备可比性,在随机分块完成时,每次使用3种方法过程中所利用的随机分块需要具备一致性.利用3种方法聚类统计上述数据集,测试3种方法在数据总量不同分块时的ARI值,测试结果如表2所示.

表2 3种方法在不同分块时的ARI值
当数据集维度较小时,3种方法分块数量越大,ARI值越大,聚类统计效果越好;当数据集维度较大时,3种方法的分块数量越小,ARI值越大,聚类统计效果越好.合理划分分块大小,可提升3种方法的聚类效果.根据表2可知,当数据集维度以及分块比例不同时,本文方法的ARI值明显高于另外两种方法,本文方法的ARI值波动范围是0.50至0.81,方法1的ARI值波动范围是0.06至0.54,方法2的ARI值波动范围是0.13至0.58.上述实验证明:本文方法在不同数据集维度及分块比例时的ARI值最高,且最低ARI值也高于标准值0.5,聚类统计效果较优.
测试3种方法在聚类统计不同稀疏度等级的数据集时的HR值及执行时间,测试结果如图1与表3所示.
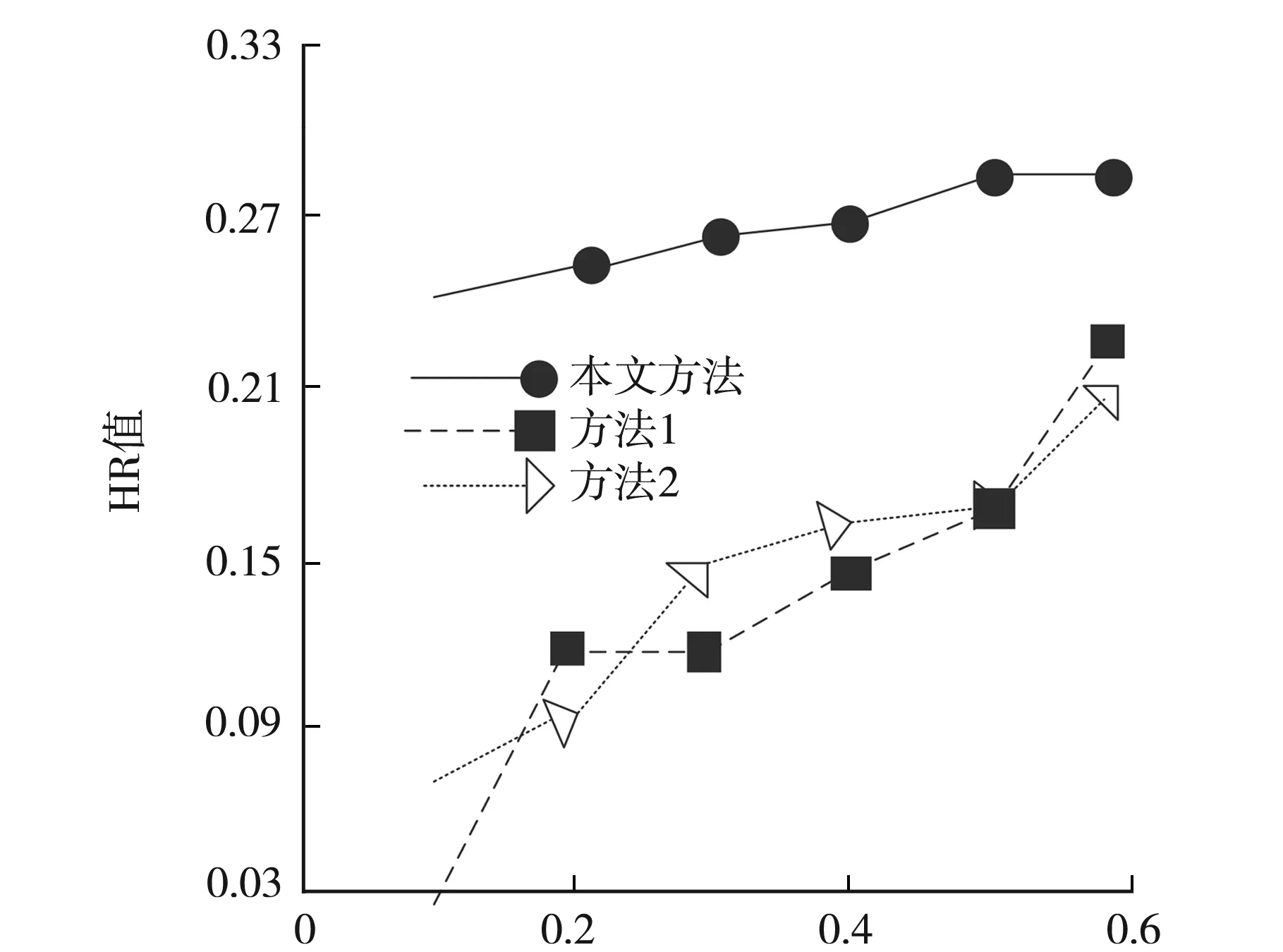
稀疏度等级图1 HR值测试结果
数据集稀疏度等级越低代表其越稀疏.由图1可知,随着稀疏度等级的逐渐提升,3种方法的HR值均有所增长,在不同稀疏度等级时本文方法的HR值均最高、变化幅度最小,且最低HR值也在0.2之上,其余两种方法仅有在稀疏度等级为0.6时其HR值才超过0.2.上述实验证明:在聚类统计不同稀疏度等级的数据集时,本文方法的HR值最高,且受稀疏度影响较小.

表3 聚类统计执行时间(μs)
根据表3可知,在数据集稀疏度等级较低时,方法1与方法2无法完成聚类统计.随着稀疏度等级逐渐提升,3种方法的聚类统计执行时间逐渐缩短,本文方法的执行时间最少.上述实验证明:本文方法适用于稀疏度较低的数据聚类统计,且聚类统计效率较高.
3 结 论
设计了基于模糊数学的高维稀疏数据聚类统计方法,以FCM算法为基础,在此基础上加以改进,解决局部最优问题,合理划分数据集的分块比例,从而提升了聚类统计效果,也降低了数据集稀疏度等级对聚类统计效果的影响,提升了聚类统计效率.

