有轨电车基于工况识别的强化学习能量管理策略

莫浩楠 杨中平 林 飞 王 玙 安星锟

（北京交通大学电气工程学院 北京 100044）

0 引言

随着城市建设规模的不断扩大，人们对轨道交通的需求越来越高，环境保护意识也不断增强。由于有轨电车相比于电动客车具有载客量大、运行速度快、污染少等优点，因此大力发展有轨电车将会缓解城市交通压力，提高出行效率[1]。其中车载储能的供电方式改善了城市景观，提高了出行的安全性[2]，然而单一的储能元件难以满足有轨电车在运行时能量和功率的全部需求，需要结合高能量密度和高功率密度的储能元件进行混合储能。

混合储能系统需要提供有轨电车全部牵引能量以满足其在运行过程中的速度需求，并且能够充分吸收再生制动能量，实现能量循环利用。其中能量管理策略的设计至关重要，其首要任务是在满足驾驶员需求功率前提下，实现对动力源功率优化分配，使整车性能最佳。然而，实际驾驶工况的不确定性和扰动性极大地增加了能量管理策略的设计难度。为此，开发高效、适应性强的能量管理策略是目前研究的关键问题。

近年来，针对混合储能系统的能量管理策略有多种，主要分为两大类：基于规则的能量管理策略和基于优化的能量管理策略。其中，基于规则的能量管理策略分为逻辑阈值法[3-4]、比例法[5]、模糊控制法[6-7]等，主要通过系统需求功率及储能系统的状态进行判断，从而做出实时的功率分配。该类方法由于控制逻辑简单、实用性强、实时响应快，在工程领域受到了广泛的应用。但控制逻辑的设定主要依据设计人员的工程经验，无法实现优化控制，若规则设置不合理，则会降低系统的控制效果。

基于优化的能量管理策略主要有全局优化[8-10]和实时优化[15-21]的策略。其中全局优化的算法需提前获知整个行驶工况，计算量大，无法直接应用于实时控制系统。常见的做法是根据离线优化的结果提取相应的规则，转换为在线的能量管理策略，或者通过结合驾驶工况识别和模型预测控制等技术提高能量管理策略的适用性。文献[8-9]针对动态规划优化结果无法实时应用的问题，从优化结果提取相应的规则，提出新的基于规则的能量管理策略。这种以离线指导在线的方法未考虑驾驶条件变化较大时对能量管理策略产生的影响。文献[11-12]采用神经网络对驾驶工况进行实时识别，结合全局优化算法的结果提取功率分配规则，并存储于控制模块中以供不同工况选择。这种方法虽然对不同工况下的能量管理策略进行了优化，但其优化结果受限，不能实现准确控制。为了使得能量管理策略更加适应当前驾驶工况，文献[13-14]引入了模型预测算法，将整个行驶工况内的全局最优问题转换为预测时域内的局部优化问题，通过滚动优化不断更新预测时域内未来行驶状态，获得优化结果。但这种方法很大程度上依赖对未来工况预测的精准性，并且不能得到全局最优解。

目前，机器学习、深度学习等人工智能算法已经应用到了混合储能实时能量管理策略中。强化学习是一种机器学习算法，在机器人控制、交通运输和运筹学等领域有着广泛的应用[15]。文献[15-18]将强化学习应用到求解插电式混合动力车辆的能量管理问题中。通过强化学习离线优化结果对储能系统进行实时控制，并较好地优化了燃油经济性。强化学习对工况变化具有一定的鲁棒性，但它的优化性能只有在相似的工况中才能得到保证。文献[19-21]引入了Kullback-Leibler偏异率，通过实时递归算法更新需求功率状态转移概率矩阵，开发基于强化学习的在线能量管理策略，使其更加适应当前驾驶工况，提高了能量管理策略的适用性和鲁棒性。

由于有轨电车起停频繁且系统功率等级高，通过在线更新强化学习策略的方法在有轨电车中受到限制。本文针对有轨电车的驾驶工况及大功率应用场合，提出了基于工况识别的强化学习能量管理策略。

本文首先对有轨电车混合储能系统进行介绍，根据实车驾驶历史数据构建了有轨电车驾驶工况；然后通过强化学习算法得到了不同驾驶工况下的能量管理策略，并采用改进的学习向量量化（Learning Vector Quantization,LVQ）神经网络对当前的驾驶工况进行识别，有轨电车根据当前识别的工况选择相应的最优控制表实时做出决策；最后采用实车运行数据进行仿真与实验，验证了该策略的有效性及可行性。

1 有轨电车储能系统建模与工况构建

1.1 混合储能系统建模

对于混合储能系统而言，不同的储能元件通过不同的储能方式连接到公共直流母线上，通过双向DC-DC变换器控制不同的电压等级之间的功率流动。由于钛酸锂电池安全性高、能量密度和功率密度兼具，超级电容充放电速度快、功率密度高且循环寿命长，为此，本文采用钛酸锂电池和超级电容进行混合储能，由戴维南定理可知，储能系统串并联以后其等效电路模型依然不变，系统拓扑结构如图1所示。

图1 混合储能系统拓扑结构Fig.1 Topology of hybrid energy storage system

该拓扑钛酸锂电池系统通过DC-DC并联到直流母线，超级电容系统直接并联到直流母线。钛酸锂电池功率可通过DC-DC直接控制，可以通过控制电池的充放电电流，延长其寿命周期，适用于以超级电容为主要供电的场合。其中，钛酸锂电池系统使用模型为一阶模型，采用Arbin单体测试仪测得其单体开路电压Vcbocv、内阻Rcbo、极化电阻Rcbp随荷电状态（State of Charge,SOC）变化曲线如图2所示。

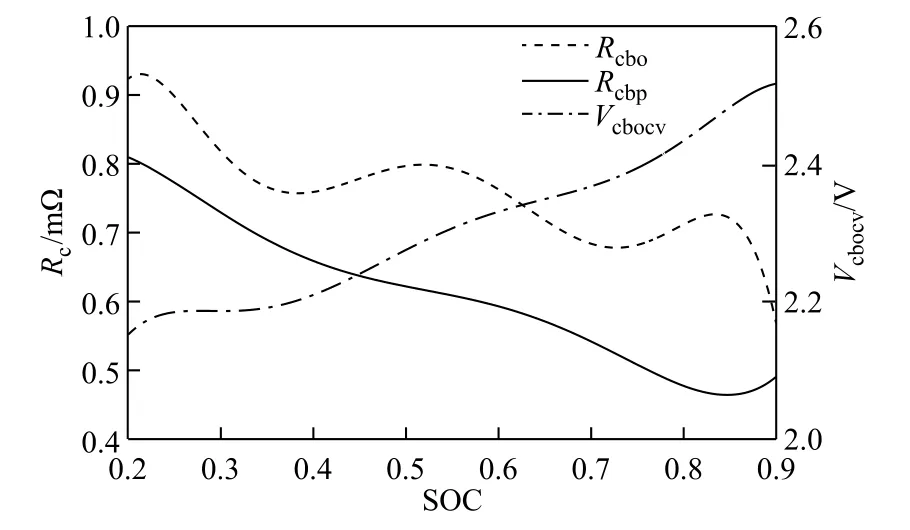
图2 Rcbo、Rcbp和Vcbocv随SOC的变化曲线Fig.2 Rcbo,Rcbp and Vcbocv vs.SOC

锂电池系统离散化的电流、极化电压、外电压和时间常数表达式为

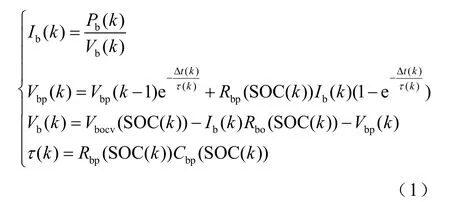
式中，k为离散时间常数；Ib为锂电池系统电流；Δt为时间间隔；τ为时间常数；Rbp、Cbp、Rbo分别为电池系统的极化电阻、极化电容、欧姆内阻；Vbocv、Vb、Vbp分别为电池系统开路电压、端电压及极化电压；Pb为锂电池系统端的功率。

本文使用安时积分法计算钛酸锂电池系统荷电状态SOC，表达式为

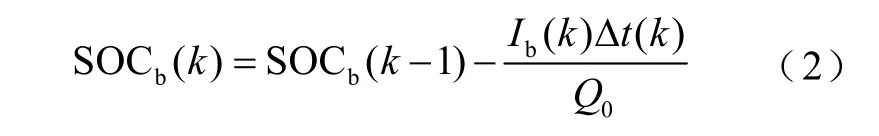
式中，Q0为钛酸锂电池系统总电荷量。

超级电容系统采用模型为内阻阻值不变的串电阻模型。超级电容系统离散化的开路电压、外电压和电流表达式为

式中，Vscocv、Vsc分别为超级电容系统的开路电压与端电压；Isc为超级电容系统的电流；Rsc为超级电容系统内阻；Csc为超级电容系统容值；Psc为超级电容系统端的功率。

采用电压平方的关系表达超级电容系统的SOC，表达式为

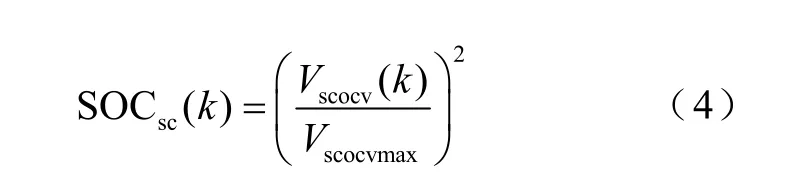
式中，Vscocvmax为超级电容系统的额定电压。

1.2 有轨电车驾驶工况构建

本文提取武汉东湖线有轨电车连续运行10天的数据，包括工作日与周末。该数据从有轨电车车载监测装置中获取，记录有轨电车自出库至回库的全部运行状态，采样频率为1Hz。有轨电车运行时间为6:30～22:00，发车间隔约为6min，运行时长为15.5h。采用短行程分析法对有轨电车驾驶工况进行构建。不同于非轨道交通车辆，有轨电车的运行路径固定，且在运行时需遵循发车间隔、限速等要求，有较为明显的规则性。定义有轨电车起点和终点的加速度和速度都为0的时刻之间的行程为短行程，如图3所示。将数据处理后得到2 782个短行程。

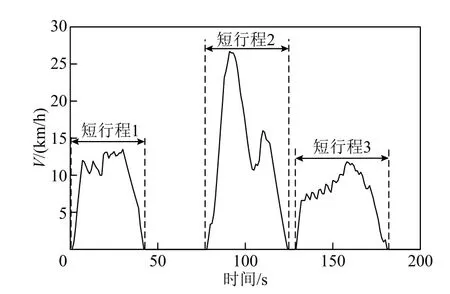
图3 短行程分割示意图Fig.3 Schematic diagram of short stroke division

提取每段短行程的特征参数，选取15个重要特征参数反映有轨电车短行程的运行信息，代表性特征值见表 1。定义低速vlow∈(0,20]km/h，中速vmid∈(20,40]km/h，高速vhigh＞40km/h。

表1 代表性特征值Tab.1 Representative eigenvalue

为了消除单位不同带来的影响，将原始特征参数进行标准化处理，并采用主成分分析法对标准化后的数据进行降维处理以减小数据重叠。选择累积贡献率达到80%以上前四个主成分代表原始变量。主成分贡献率见表2。

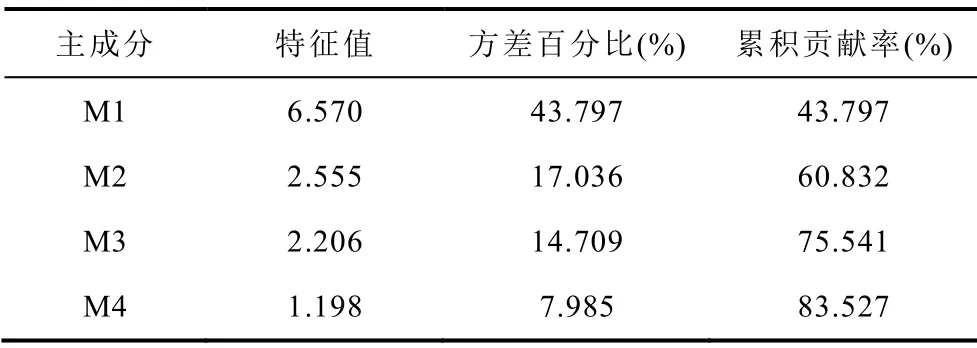
表2 主成分贡献率Tab.2 Principal component contribution rate

根据东湖线有轨电车的行驶状况，可以将短行程片段划分为三类，采用K均值聚类进行分析，其聚类结果及各工况特征参数见表3。

由表3可以看出，三种工况特征参数区分明显，对各工况特征参数进行分析。工况一数目最少，平均运行速度、平均加速度和减速度绝对值、高速运行时间占比最高，称为高速工况。工况二平均运行速度、平均加速度和减速度绝对值最低，低速运行时间占比高达86.18%，称为低速工况。工况二特征参数介于工况一和工况三之间，称为中速工况。

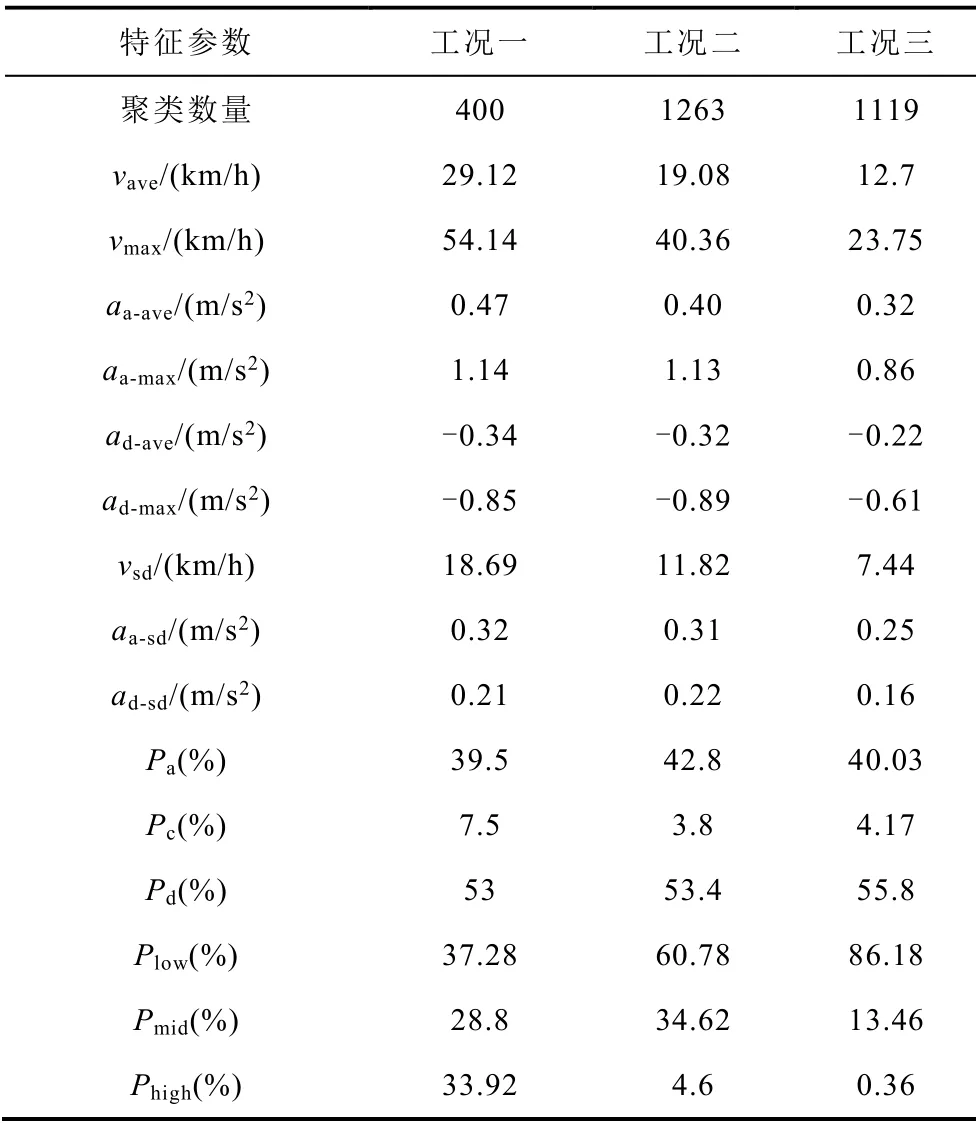
表3 工况聚类结果及特征值Tab.3 Working condition clustering results and eigenvalues

2 基于工况识别的强化学习能量管理策略

强化学习（Reinforcement Learning,RL）是一种自适应最优控制方法，其目的是在观察和分析系统行为的基础上，通过试错学习作出最优决策，以改进系统性能，得到的策略是状态到动作的映射，与时间无关，因而可以直接应用到在线控制。对于混合动力有轨电车而言，运行过程中的牵引制动功率是一个随机状态，这样一个随机过程满足马尔可夫性质，即从一个状态转移到另一状态的概率只与当前系统所处状态有关，与之前系统所处状态无关。因此，混合动力有轨电车的能量管理问题本质上是一个马尔可夫决策过程（Markov Decision Process,MDP）。

2.1 目标函数及约束条件

有轨电车能量管理问题可以表示为在约束范围内最小化目标函数的约束优化问题，目标函数选择储能系统的能量损失。

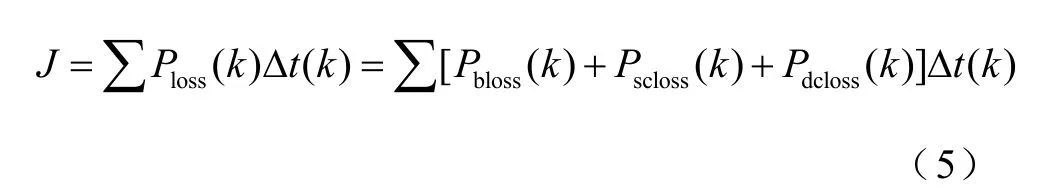
式中，Ploss为储能系统总损耗；Pbloss为电池内阻损耗；Pscloss为超级电容内阻损耗；Pdcloss为DC-DC损耗。各系统损耗通过式（6）计算。

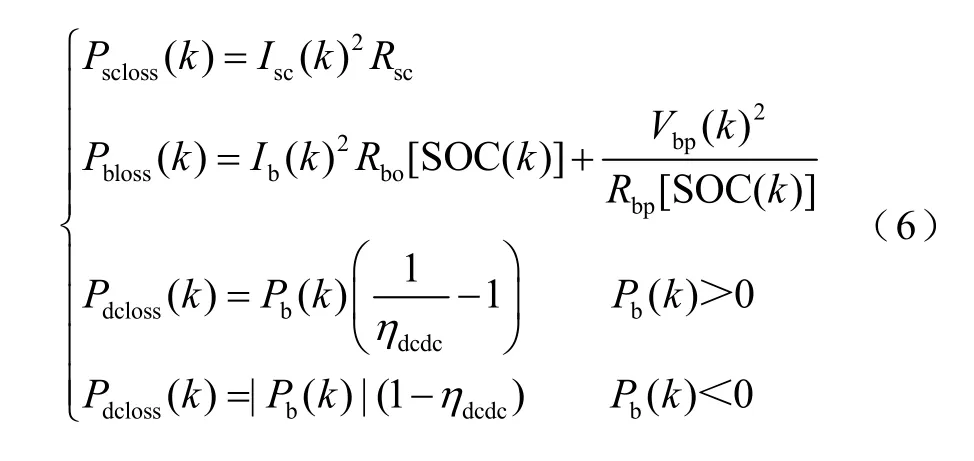
式中，ηdcdc为DC-DC转换器的效率。

为了保证储能系统工作在合理范围内，能量管理问题受到以下约束条件的限制。

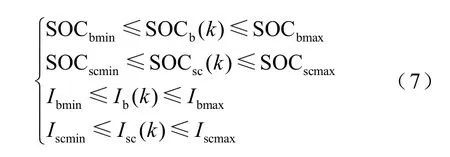
式中，SOCbmax和SOCbmin分别为电池系统荷电状态的上、下限；SOCscmax和SOCscmin分别为超级电容系统荷电状态的上、下限；Ibmax和Iscmax分别为电池和超级电容系统的最大放电电流；Ibmin和Iscmin分别为电池和超级电容系统最大充电电流。

2.2 转移概率矩阵

基于强化学习能量管理策略的一个基本步骤是对列车运行过程中的需求功率进行建模。需求功率变化可以看作是一个平稳的马尔可夫过程，而需求功率状态转移概率矩阵可以通过式（8）最邻近法和最大似然估计法计算。

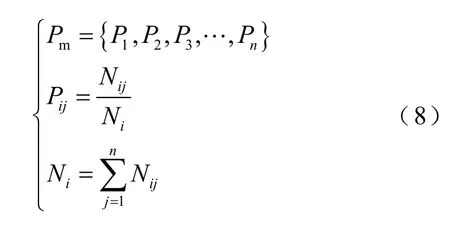
式中，n为需求功率状态数量；Pij为在一定速度下功率Pi到Pj的转移概率；Nij为Pi到Pj的次数；Ni为状态Pi产生的总次数。

计算不同驾驶工况下的状态转移概率过程如图4所示，根据1.2节构建的三种驾驶工况提取状态转移概率。

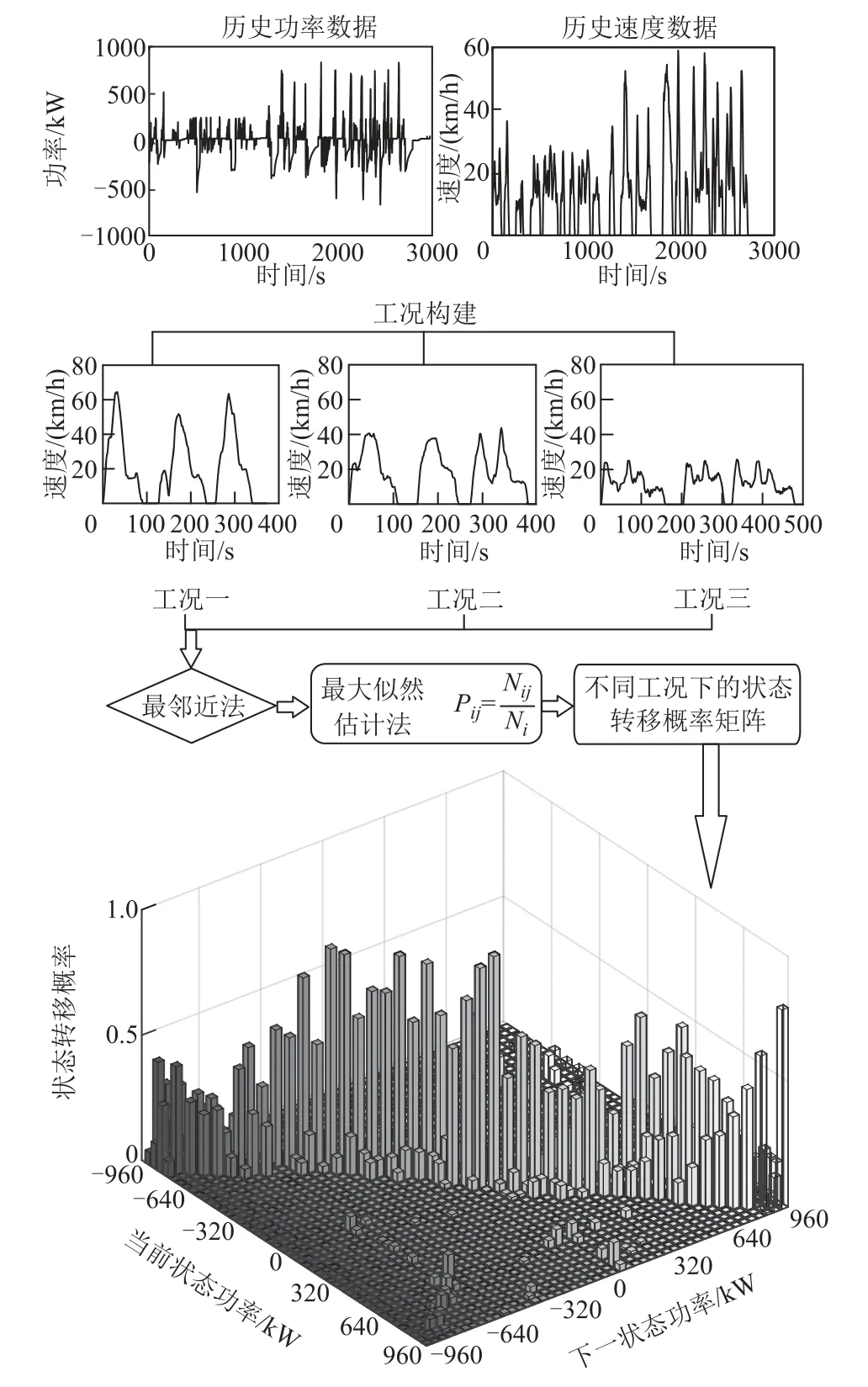
图4 不同工况状态转移概率计算过程Fig.4 Calculation process of state transition probability under different working conditions

2.3 基于工况识别的强化学习控制策略建立流程

对于有轨电车能量管理问题，选择有轨电车运行速度、有轨电车功率需求、电池SOC和超级电容SOC作为状态变量：st∈S= {V,Preq,SOCb,SOCsc}。电池输出功率为决策变量：at∈A={Pbat}。即时奖励定义为功率损耗的倒数：rt∈R= {1 /Ploss(st,at)}。

基于强化学习的控制策略是一个从状态到动作的映射函数π：S-A，当π被用作一系列完整的决策策略时，状态s的最优值被定义为折扣回报函数的期望之和，即

式中，γ∈ [0,1]为折扣因子。

根据状态转移概率及贝尔曼最优方程的定义，可以将式（9）改写为

基于给定的最优值函数，可通过式（11）计算最优策略。

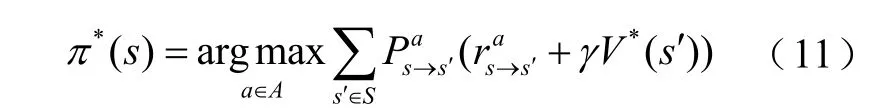
对于状态s和动作a所对应的值函数可用Q来表示，即

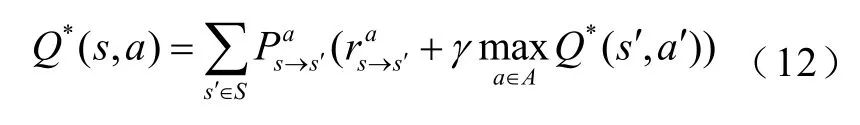
在Q-learning算法中，Q值可以按照式（13）进行更新。

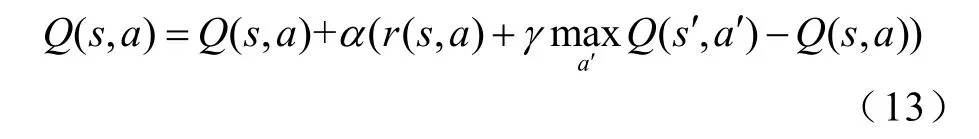
式中，n为迭代次数；α为算法中的学习率，α∈ [0,1]。学习率越大收敛速度越快，但会导致过拟合问题。本文选择的学习率为。

由于不同工况下的功率状态转移概率有较大差异，若直接依据历史行驶数据构建状态转移矩阵，会使系统控制性能下降，降低鲁棒性。为使得能量管理策略能更加适应有轨电车复杂驾驶工况，将具有相似的马尔科夫链模型的驾驶工况进行归类，并采用改进的LVQ神经网络进行工况识别，以规避驾驶工况变化较大时对能量管理策略的影响。如图5所示，LVQ神经网络主要由输入层、竞争层和线性输出层组成，通过不断训练输入层和隐含层之间的权值进而获得更好的分类结果。输入层的15个输入节点分别对应行驶工况的15个特征参数，竞争层选择80个神经元，线性输出层神经元个数为3，对应着期望识别的三种工况。

图5 LVQ神经网络训练结构Fig.5 LVQ neural network training structure

由于LVQ 网络的初始权值向量对网络训练的影响很大，为了获得良好的初始权值，提高网络分类性能，本文采用粒子群算法对网络初始权值进行优化，目标函数为训练数据预测误差。

式中，Ti为神经网络训练输出数据；Yi为神经网络预测数据；abs(·)为绝对值函数。

采用移动时间窗口的形式进行工况数据的更新，识别窗口T=120s，预测窗口Tf=20s。通过实时计算时间窗口T内的工况特征参数进行工况识别，作为未来Tf窗口的驾驶工况。对东湖线某天一段时间内的实车数据进行实时工况识别，识别结果如图6所示。

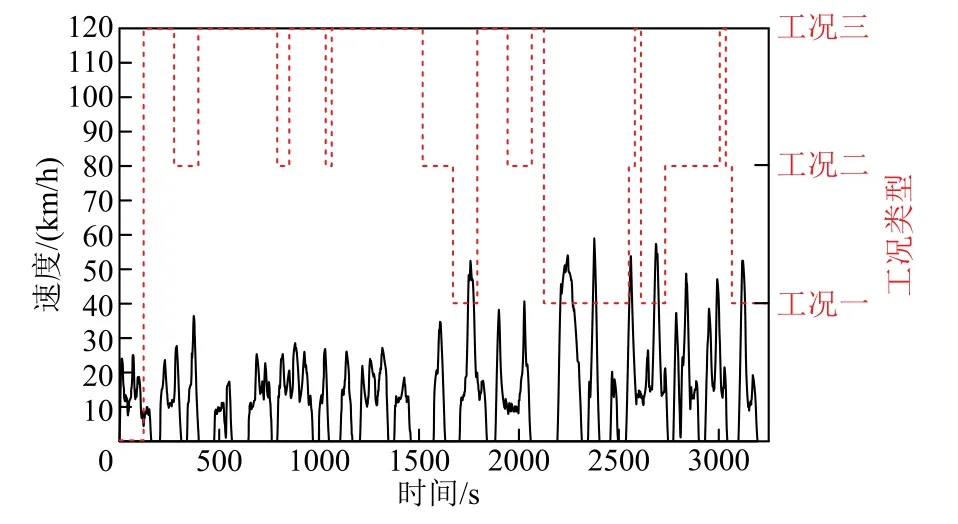
图6 工况在线识别结果Fig.6 Working condition online recognition result

由于采用移动窗口的形式进行工况识别，窗口内的特征参数可能和当前短行程的特征参数有一定的差异，使得识别结果出现一定的误差，但由于不同工况特征参数差异较大，LVQ神经网络能够大致识别工况类型。

基于工况识别的强化学习能量管理策略流程如图7所示，主要包括离线优化求解和在线实时控制两个流程。在线实时控制时，通过截取时间窗内的实际工况信息进行在线工况识别，有轨电车根据当前识别工况、运行速度、需求功率及储能系统SOC并结合该类工况下的最优控制表实时输出电池需要承担的功率。

图7 基于工况识别的强化学习能量管理策略建立流程Fig.7 Process of establishing RL energy management strategy based on working condition recognition

3 案例分析

3.1 仿真条件及优化结果分析

本文以东湖线实车驾驶工况，采用遍历方法对混合储能系统进行容量配置，得到满足边界条件的储能系统参数见表4。

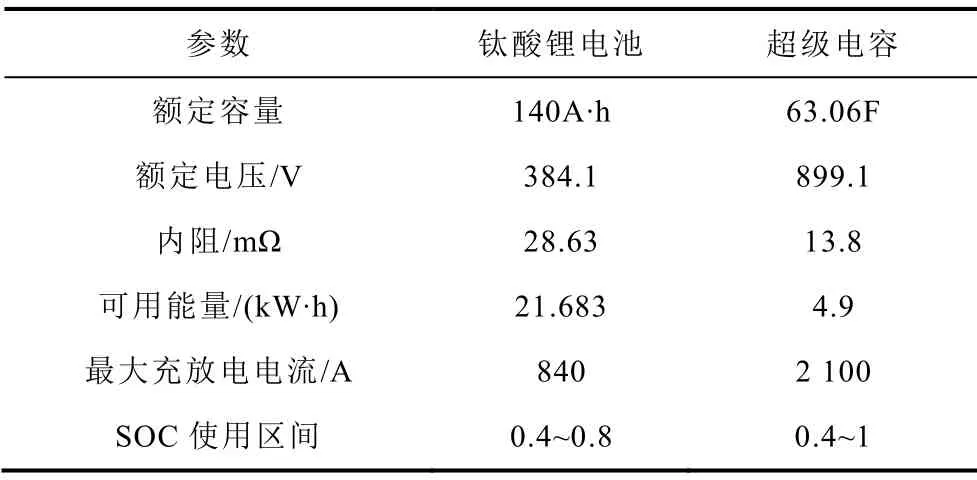
表4 储能系统参数Tab.4 Energy storage device parameters

以工况一为例，图8给出在速度为40km/h时强化学习算法中每500次迭代后的Q值平均误差变化曲线。选择折扣因子为0.9，并采用贪婪概率1-[1/lg(n/100+2.8)]进行动作选择。在迭代初期，随机选择动作概率较大，主要选择探索环境扩充样本，随着训练次数的上升，随机选择动作概率逐渐减小，经过充分“试错”学习之后，由探索环境状态逐渐转为利用知识状态。当迭代次数为5 000万次时，Q值平均误差逐渐趋近于0，算法达到收敛。

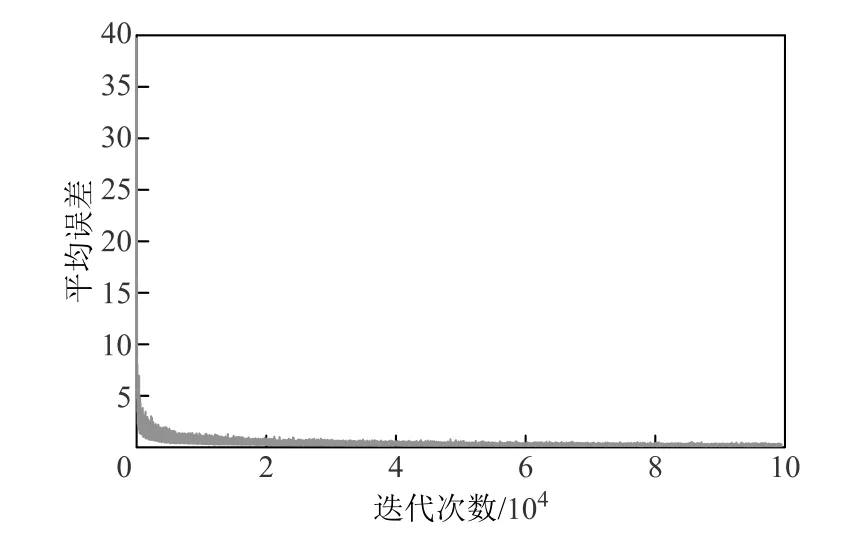
图8 每500次迭代Q值平均误差Fig.8 Mean discrepancy of Q value per 500 iterations

图9为在工况一条件下，速度为40km/h，不同需求功率等级下的动作变量变化情况。从图中可以看到，钛酸锂电池输出功率随着钛酸锂电池SOCb、超级电容SOCsc和需求功率变化而变化，具有一定的变化趋势，但无明显的规则。当系统牵引功率较小时主要由超级电容提供功率，且超级电容SOCsc较低时，电池提供较高功率。当系统制动功率较小且超级电容SOCsc较高时，主要由电池吸收制动功率。当系统牵引、制动功率较高时，由于电池额定功率限制，电池和超级电容分别承担相应的功率。

图9 不同状态下动作变量分布Fig.9 Distribution of action variables in different states

需要注意的是，由于有轨电车到站充电的过程不具有马尔科夫性，由强化学习得到的能量管理策略只在有轨电车运行过程中使用，到站进行恒流充电，采用优先超级电容充电策略。

3.2 能量管理策略验证及对比分析

以一条实车驾驶数据作为输入条件，如图10所示，来验证工况识别的强化学习能量管理策略的优化效果，其中充电站以500A恒流充电。

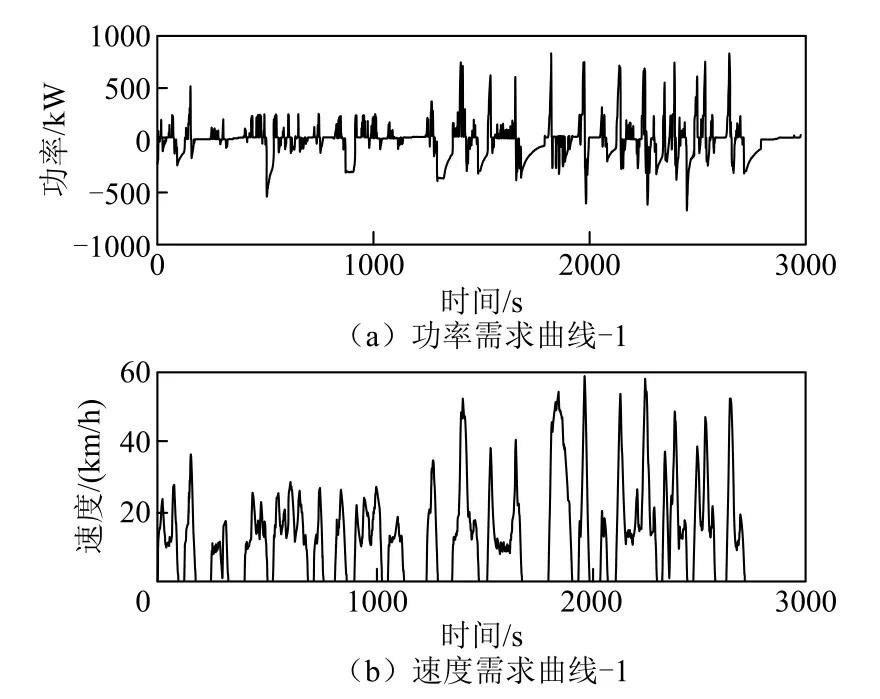
图10 实车驾驶曲线-1Fig.10 Real vehicle driving curve -1

图11为储能系统功率分配曲线及SOC曲线，从中可以看出，由于钛酸锂电池系统SOC充足，制动功率基本都由超级电容系统吸收，且在牵引工况时，充分利用超级电容供电，减少了电池的使用，在一定程度上可以增加电池的使用寿命并降低储能系统损耗。

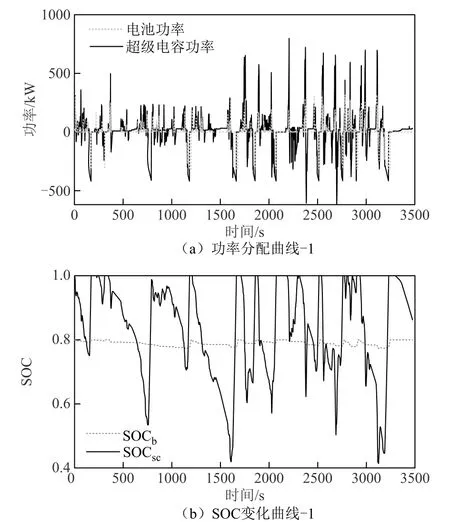
图11 储能系统功率分配曲线及SOC变化曲线-1Fig.11 Energy storage system power distribution curve and SOC change curve -1

为进一步验证基于工况识别的RL策略的有效性，将其与无工况识别的RL策略和基于规则的最优比例法进行对比。

图12a对三种策略超级电容的SOC 进行了对比。三种方法SOC轨迹均有差异，由于超级电容SOC使用范围限制，其SOC都在0.4～1。可以看出基于RL的策略充分使用了超级电容。

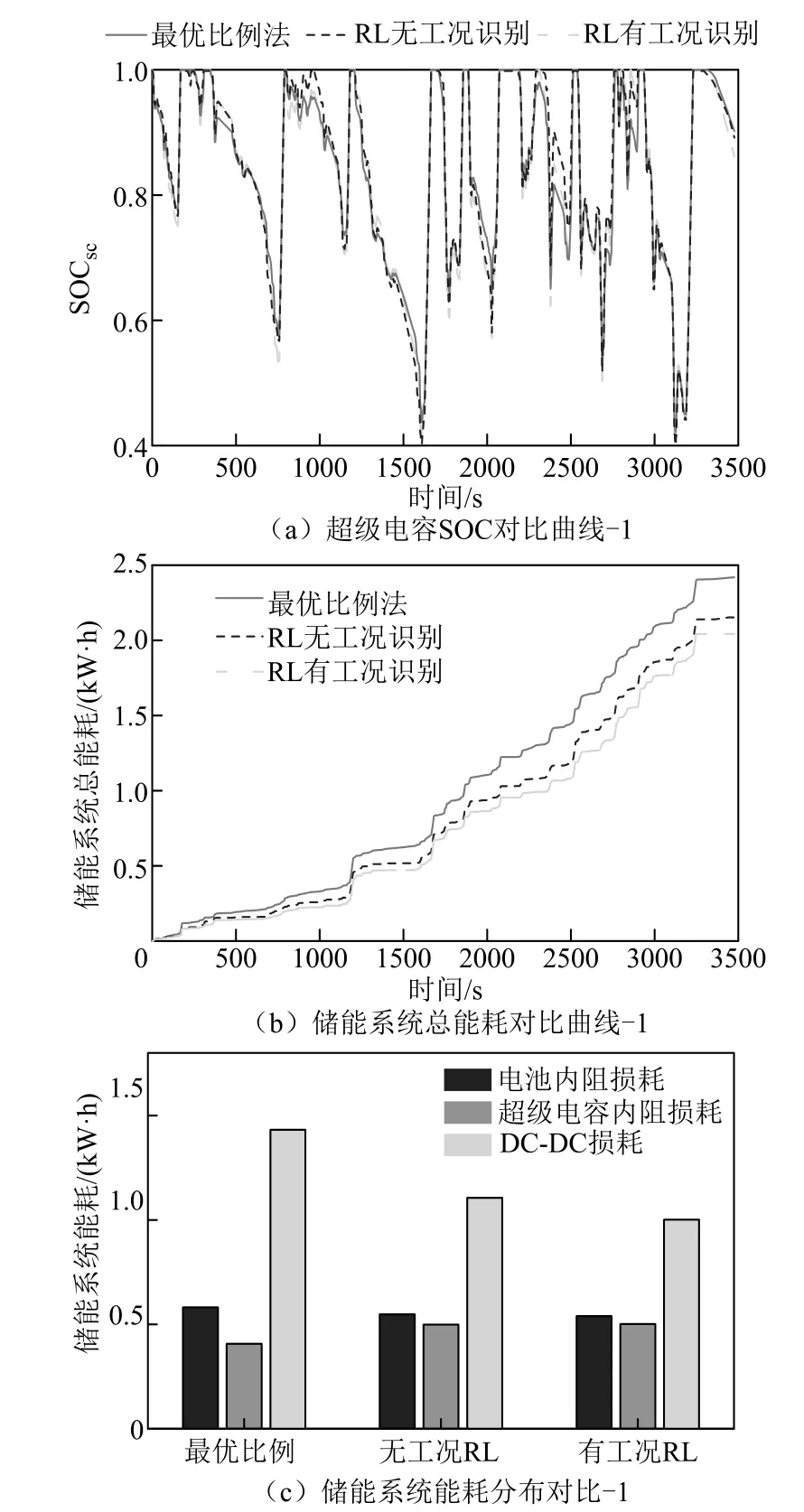
图12 三种策略下超级电容SOC及总能耗对比-1Fig.12 Comparison of super capacitor SOC and total energy consumption under three strategies -1

图12b和图12c对三种策略储能系统能耗进行了对比。从储能系统能耗分布来看，基于RL的策略电池内阻损耗和DC-DC损耗都会减小，超级电容内阻损耗会增加，但储能系统总能耗都会减小。三种策略下储能系统能耗对比见表5。从表5中可以看出，无工况识别的RL策略总能耗降低11.2%，有工况识别的RL策略总能耗降低了15.7%，均能减少储能系统能量损失，提高系统效率。可以看出，在进行强化学习离线优化时，对有轨电车驾驶工况进行聚类分析，将具有相似马尔科夫状态转移概率的工况归为一类，可以得到更好的节能效果。

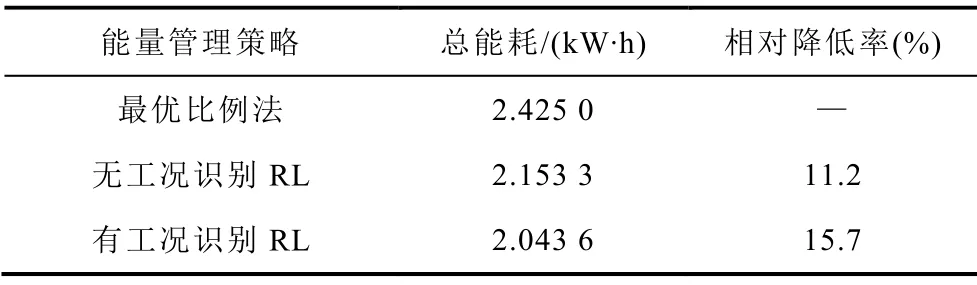
表5 三种能量管理策略下的储能系统能耗对比-1Tab.5 Comparison of energy consumption of EMS under three energy management strategies -1

为充分验证基于工况识别强化学习策略的适应性，将求得的策略应用于东湖线另外一条实际驾驶工况，其中充电站以1kA恒流充电，如图13所示。

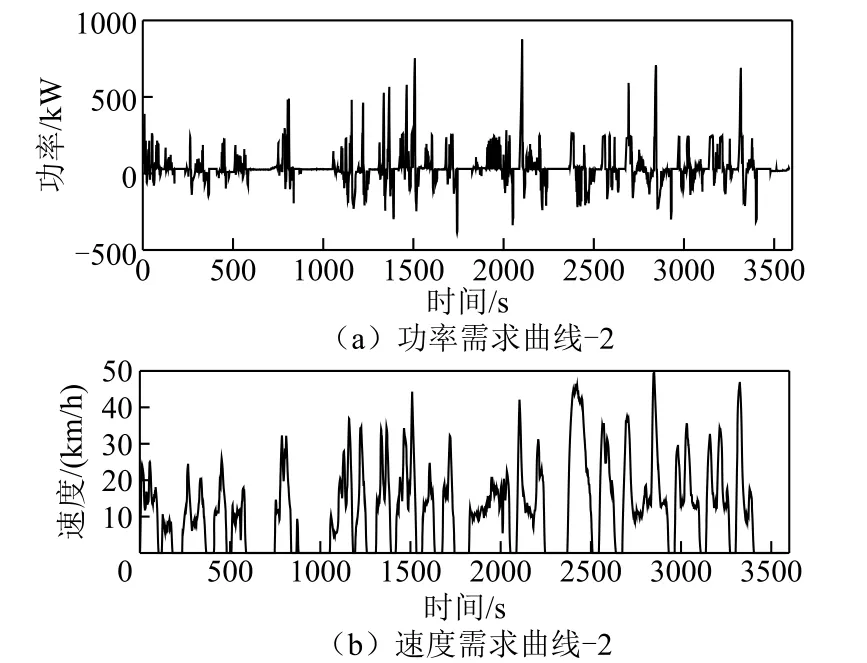
图13 实车驾驶曲线-2Fig.13 Real vehicle driving curve -2

得到的基于工况识别的强化学习策略适应性验证工况的功率分配曲线及储能系统SOC曲线如图14所示。

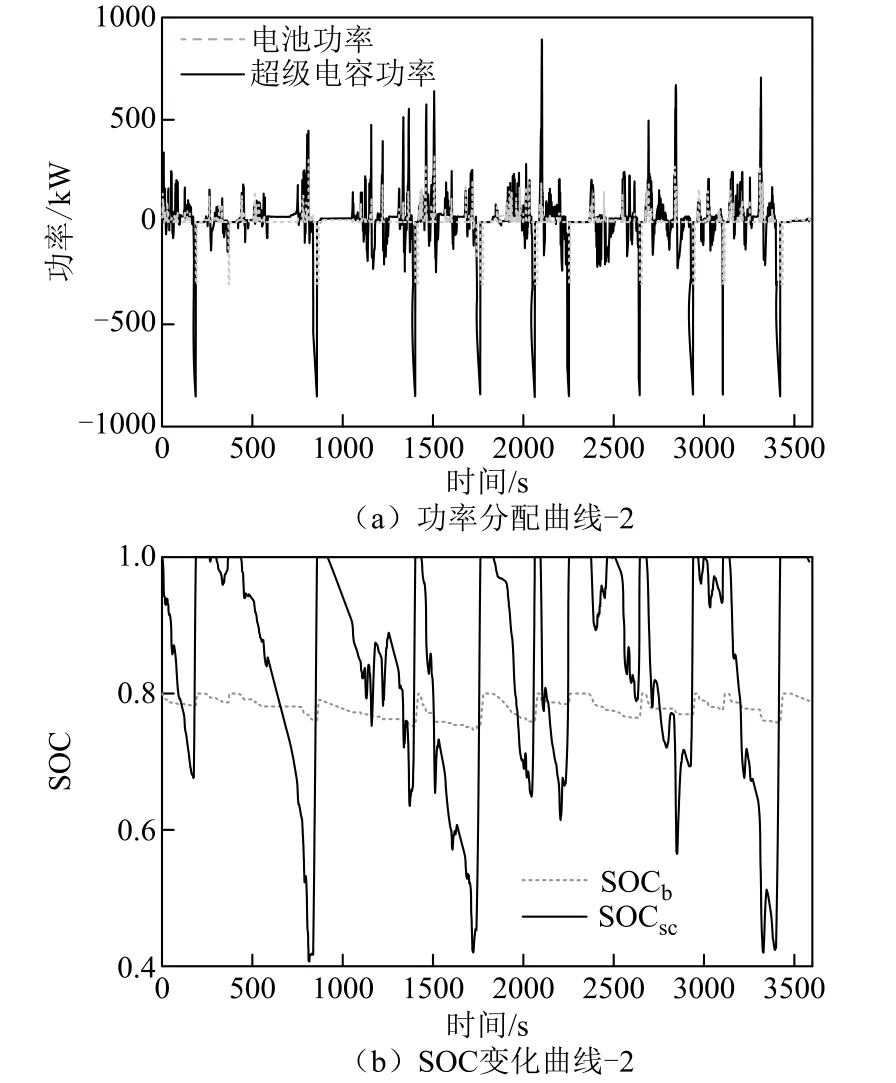
图14 储能系统功率分配曲线及SOC变化曲线-2Fig.14 Energy storage system power distribution curve and SOC change curve -2

将适应性验证工况的三种能量管理策略进行对比，分别得到超级电容SOC曲线及储能系统能耗，如图15和表6所示。

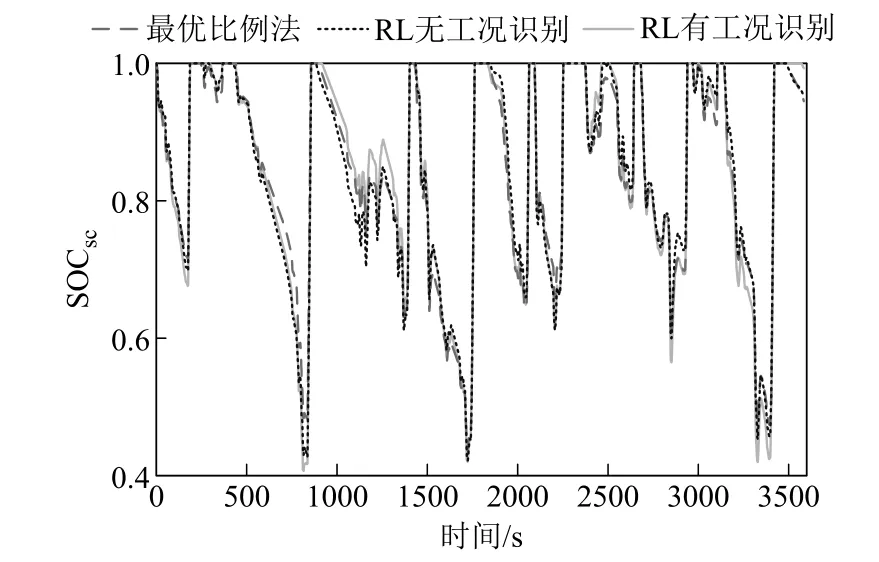
图15 三种策略下超级电容SOC对比-2Fig.15 State of charge of super capacitors comparison under three strategies -2

表6 三种能量管理策略下的储能系统能耗对比-2Tab.6 Comparison of energy consumption of EMS under three energy management strategies -2

可以看到，适应性验证工况与原工况的仿真结果趋于一致。通过改变三种能量管理策略的验证工况，得到基于工况识别的强化学习策略在不同工况下均优于无工况识别强化学习策略及最优比例法，从而说明强化学习算法对不同工况的适应性。

3.3 实验验证

为验证基于工况识别的强化学习策略的在线决策的有效性及可行性，在如图16a所示的90kW电池-超级电容混合储能系统实验平台上进行实验。实验平台的储能系统基本参数见表7。

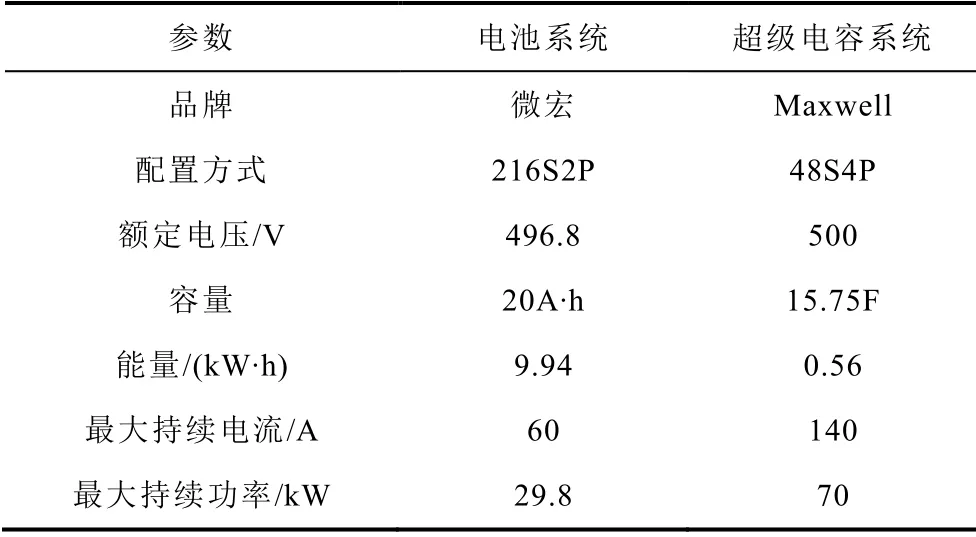
表7 混合储能平台参数Tab.7 Hybrid energy storage platform parameters

本实验主要验证混合储能系统在不同工况下的强化学习能量管理策略的控制效果。设计验证实验接线如图16b所示。上位机通过CAN通信，接收由电机通过DSP传输的数据，输入至Matlab软件中进行工况在线识别，并通过强化学习已优化出的最优控制表进行在线决策，采用Python读取功率分配结果，并通过CAN通信将指令传回DSP，使混合储能系统执行充放电指令。上位机通过以太网-CAN转换模块输出信号，与电池的BMS模块所输出的信息并联在CAN总线上。

图16 混合储能实验验证平台Fig.16 Hybrid energy storage experimental verification platform

以有轨电车实际运行数据作为输入，由于实验平台功率等级的限制，对列车负载曲线进行等比例缩放处理，缩放后最大功率约为40kW，如图17所示。

图17 实验输入曲线-1Fig.17 Experimental input curve -1

以最优比例法、无工况识别的强化学习策略及基于工况识别的强化学习策略依次进行实验。所得电池、超级电容的电流曲线、超级电容的电压曲线及母线电压曲线如图18所示。

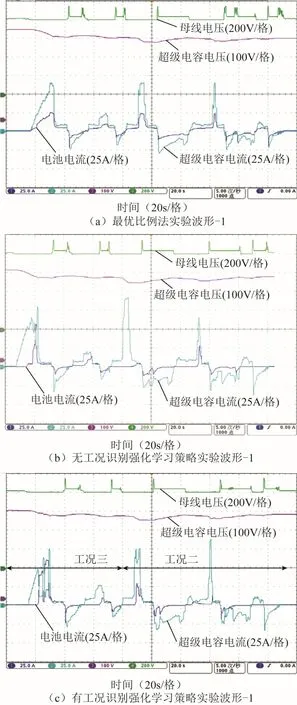
图18 三种策略下的实验波形-1Fig.18 Three strategys experimental waveforms -1

采用另一条实际运行数据进行实验验证，如图19，验证强化学习策略对不同工况的适应性。

图19 实验输入曲线-2Fig.19 Experimental input curve -2

图20 三种策略下的实验波形-2Fig.20 Three strategys experimental waveforms -2

通过90kW样机实验可得，在混合储能系统实际运行时，通过上位机向控制器实时发送指令，控制混合储能系统动作，储能系统能够跟随功率分配结果进行相应充放电。由实验波形可以看出，基于强化学习的能量管理策略能够根据系统状态做出实时决策，充分利用超级电容进行供电以减少系统损耗。通过加入对工况的在线识别过程，可提升在线决策过程中的控制效果，并满足实时控制需求，实现工程应用。

4 结论

本文以有轨电车车载混合储能系统为研究对象，由于需求功率的随机性，将有轨电车的功率需求看做马尔科夫过程，并考虑到驾驶工况变化较大时对能量管理策略的影响，提出了基于工况识别的强化学习能量管理策略。通过主成分分析及K均值聚类得到了高速、中速、低速三种驾驶工况，并得到不同工况下的功率状态转移概率。采用强化学习算法得到不同工况及速度下的电池功率的动作值，并通过改进的LVQ神经网络实时识别当前的驾驶工况进而做出相应的决策，使其能够在相似工况中获得更好的控制效果。与最优比例法相比，该方法储能系统总能耗降低了约15.7%，且比无工况识别的RL能量管理策略具有更好的节能效果。将本文的策略应用于东湖线另外一条实际驾驶工况，验证了基于工况识别的强化学习策略对不同工况的适应性。通过90kW的实验平台进行模拟运行，验证了本文提出的基于工况识别的强化学习策略的有效性，证明了该策略在工程应用中的可行性。