参与调峰的储能系统配置方案及经济性分析

李军徽 张嘉辉 李翠萍 陈国航 张昊天

（1.现代电力系统仿真控制与绿色电能新技术教育部重点实验室（东北电力大学）吉林 132012 2.国网浙江平湖市供电有限公司 平湖 314200）

0 引言

近年来，我国新能源发展趋势越来越快速。以风电为例，2020年上半年，全国新增风电装机容量632万kW，截止2020年6月底，累计并网装机容量达到2.17亿kW，并且全国弃风电量及弃风率实现“双降”[1]，但部分地区弃风情况仍较为明显，风电的反调峰特性提高了电网峰谷差，给电网的稳定运行带来困难[2-4]。为缓解上述矛盾，需展开火电机组深度调峰，但深度调峰会增加机组运行成本，如何平衡经济性与调峰性能的关系是决定机组运行的关键因素[5-6]。而储能技术具有较快的响应速度，能够优化电源结构，增加系统调峰容量，储能辅助火电机组参与电网调峰可以改善电网调峰压力，减少风电高渗透地区弃风产生[7-10]。但储能技术的高成本是影响其发展的关键因素之一，故如何确定合适的储能系统配置方案，使其保证经济性的同时又具有较好的调峰效果是目前研究的热点[11]。

目前也有关于储能参与调峰容量配置的研究。文献[12-13]将储能系统用于区域能源系统，并以储能系统综合投资成本及运营成本最小为目标建立优化配置模型，并没有计及储能系统收益和系统技术性指标对其配置结果的影响；文献[14]基于容量市场合同构建用户实时电价需求响应模型，然后计及容量市场建立储能定容双层优化配置模型；文献[15]以系统总成本最低为目标建立用于优化负荷曲线的储能优化配置模型，也未计及储能收益及系统技术性指标影响；文献[16]提出一种市场机制下光伏/小水电/抽水蓄能电站的混合能源系统容量配置优化方法，旨在获得最大的经济效益。上述文献优化配置模型侧重储能经济性，而由于储能系统成本高昂，单以经济性为优化目标会减少储能系统需求，降低其应用效果。

此外文献[17]将储能系统用于电网调峰，并以净效益最大化为目标建立优化配置方法；文献[18]从储能系统的削峰填谷能力、电压质量以及功率主动调节能力三方面建立多目标优化配置模型。上述文献都将储能系统用于电网调峰，但其优化配置目标仅从经济性或技术性单方面出发，此外也并没有计及电网常规能源结构运行状态对优化调度策略的影响。而文献[19]中的储能系统优化配置模型综合考虑了储能系统的运行优化调度问题，但其配置目标函数仅考虑了储能系统的经济性。文献[20]提出一种考虑网架结构的电池储能系统配置双层优化模型，用于提高风电场运行效益，提高风电接纳量，但没有考虑储能加入后对常规电源运行经济性的影响。文献[21]基于不同的火电机组调峰手段及不同储能容量配置方案，综合考虑调峰技术性指标及经济性指标，选取最优的组合优化方案，但其从实用性角度出发，设定不同的组合方案进行指标数值计算，优化性能不佳。

双层模型能够有效降低模型求解的难度，国内外已有研究通过建立双层模型求解储能系统容量配置，文献[22]中内层模型仅将系统负荷波动最小为目标，没有兼顾系统经济性指标；文献[23]建立了同时考虑离网及并网运行状态的储能配置双层优化模型，但其目标函数也仅考虑了储能的经济性；文献[24]所提外层模型仅以储能投资效益最大为目标，考虑储能投资成本和多市场收益，没有从系统多目标角度出发，综合分析储能最优配置方案。上述文献多针对配电网侧，对储能系统的配置目标仅从经济性或技术性单方面出发，此外也没有从储能全寿命周期角度分析其经济性。文献[25]提出一种基于元模型优化算法的混合储能双层优化配置方法，其外层模型仅以储能的全寿命周期年均成本最小为目标，同时也没有计及电网常规电源对优化配置的影响；文献[26]建立了辅助单台机组自动发电控制的电池储能系统双层优化配置模型，首层为运行优化层，次层为储能配置层，但其目标仅为火电机组，对含大规模风电及火电的区域电网指导意义不佳。在模型求解方法方面，文献[27]与本文建模方法类似，上层建立配置模型，下层建立优化调度模型，但在求解时使用对偶定理改进模型等效单层模型求解；文献[28]应用于分布式电源，其上层模型为最优容量配置模型，求解时转换为单层模型，并结合其约束条件生成算法求解。本文构建双层模型，与已有研究在应用场景、建模方法以及求解算法方面均不同。

根据上述分析，本文工作主要创新点如下：①提出综合考虑储能系统参与电网调峰时经济性指标和技术性指标的储能系统优化配置方案；②考虑储能系统加入后对常规电源运行经济性的影响，以系统总调峰成本最低来优化机组及储能系统的运行状态；③计及储能系统全寿命评估储能应用的经济性，从多角度系统分析影响其经济性的主要因素。

本文提出了储能参与电网调峰的配置方案。该模型在外层优化配置模型中，综合考虑储能调峰经济性指标及系统技术性指标，构建多因素优化模型，得到兼顾经济性及技术性的储能系统最优配置方案；内层模型为储能系统优化调度模型，并且为了最大限度地消纳风电能源，调度模型综合考虑储能系统调峰作用及火电机组深度调峰作用，以系统总调峰成本最少为目标，优化储能及火电机组运行状态。

1 储能辅助电网调峰原理分析

目前电网的调峰形势为在负荷尖峰时段有足够的旋转备用空间，但在负荷低谷时期，机组的向下调节灵活性严重不足，从而导致大量弃风产生。储能辅助火电机组调峰基本原理如图1所示。

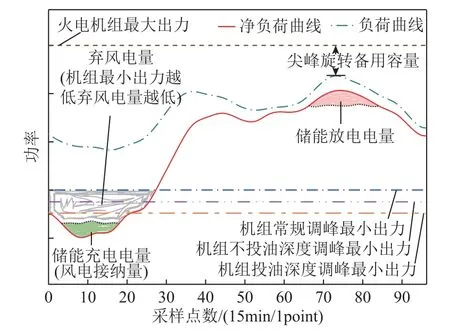
图1 储能辅助火电机组深度调峰原理Fig.1 Schematic diagram of deep peak shaving for energy storage assisted thermal power units

从图1中可以看出，储能辅助火电机组深度调峰可以有效改善电网调峰压力，减少弃风产生。而储能系统产生的调峰效果主要取决于其配置方案，配置越高其调峰效果越好，但成本也随之大幅上升。储能系统的配置应兼顾经济性指标及技术性指标。

2 系统调峰优化指标模型

2.1 系统经济性指标

2.1.1 系统成本指标

储能辅助火电机组调峰涉及的系统成本指标主要包括储能投资成本、储能运行成本、火电机组运行成本和弃风惩罚成本。

1）储能系统投资成本指标

储能系统全寿命周期内的主要成本投入为投资成本，主要由功率成本及容量成本构成，其计算公式为

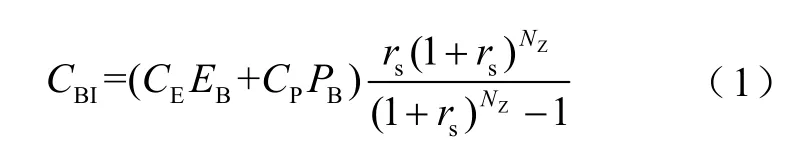
式中，EB、PB分别为储能系统容量配置及功率配置；CE、CP分别为容量配置单价及功率配置单价；rs为折现率；NZ为储能系统运行年限。

2）储能运维成本指标

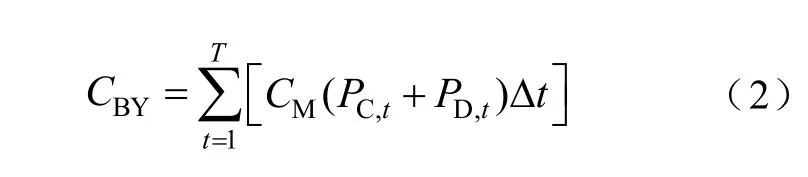
式中，PC,t、PD,t分别为t时刻储能系统充、放电功率（其值均为正）；CM为储能系统运维成本单价；T为采样总时长，本文为一天24h；t为采样时间步长，本文步长为1h。

3）火电机组运行煤耗成本指标

火电机组在常规调峰阶段的运行成本主要为煤耗成本，其计算公式为

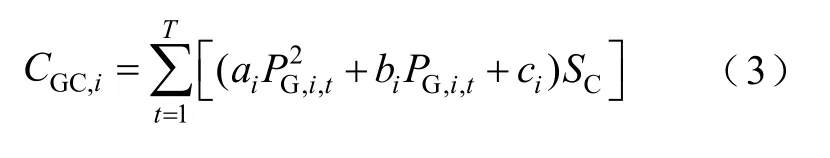
式中，ai、bi、ci分别为第i台火电机组耗量特性函数的系数；SC为当季单位煤炭价格；PG,i,t为第i台火电机组t时刻的出力。

4）机组损耗成本指标

在火电机组深度调峰过程中，会产生额外的机组损耗成本，计算公式为

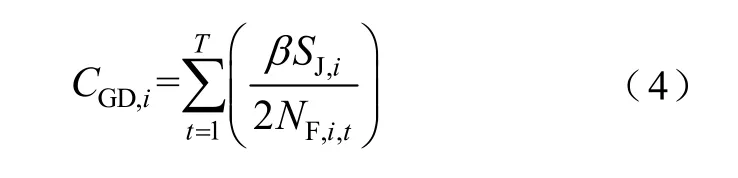
式中，β为火电厂实际运行损耗系数；SJ,i为第i台火电机组的购机成本；NF,i,t为第i台火电机组t时刻的转子致裂周次，该值与火电机组出力PG,i,t相关。

5）投油成本指标

当机组出力降低到一定水平时，还会产生额外的投油成本，其计算公式为

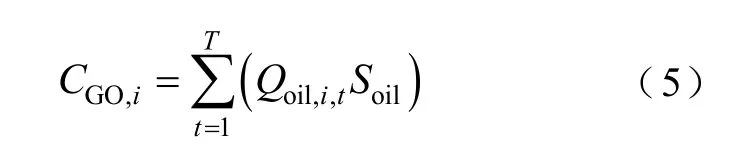
式中，Qoil,i,t为第i台火电机组投油深度调峰阶段t时刻的投油量；Soil为当季的油价。

6）弃风惩罚成本指标

为增加风电的接纳量，减少系统弃风率，设立弃风惩罚成本，其公式为

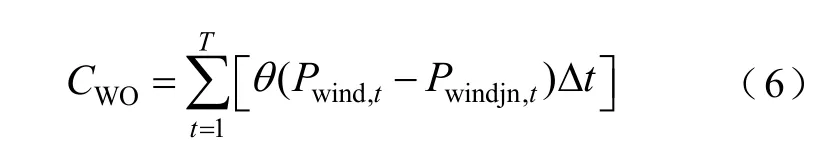
式中，θ为弃风惩罚系数；Pwind,t为t时刻风电功率；Pwindjn,t为t时刻风电上网功率。

2.1.2 系统收益指标

储能辅助火电机组调峰涉及的系统收益指标主要包括储能套利收益、储能补偿收益和火电机组深度调峰补偿收益。

1）储能套利收益指标

储能系统利用电网峰谷电价差，通过“低储高发”进行套利，其计算公式为

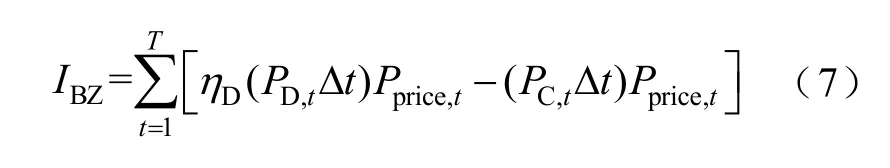
式中，ηD为储能系统放电效率；Pprice,t为电网的实时峰谷电价。

2）储能补偿收益指标

储能系统参与电网调峰运行时获得的补偿为

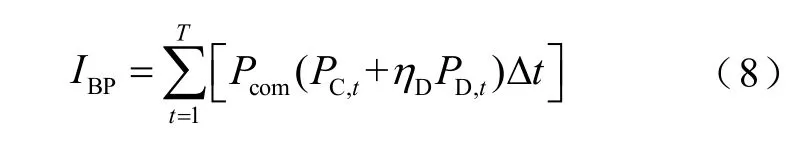
式中，Pcom为补偿单价。

3）火电机组深调补偿收益指标

为了鼓励火电机组进行深度调峰，各地出台相应的深调补偿政策，当机组处于常规调峰最低出力水平之下时给予一定补偿，其计算公式为

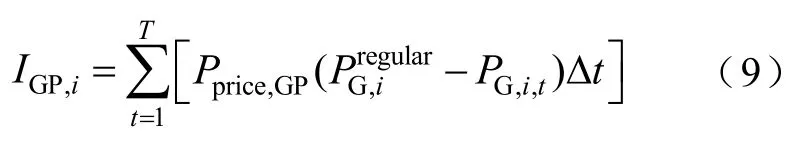
2.2 系统技术性指标

储能辅助火电机组调峰可以降低机组日出力调节量，减少弃风产生，故其技术性指标包括火电机组出力标准差改善量以及储能系统加入后的新增风电接纳量。

2.2.1 火电机组出力标准差改善量指标

系统机组出力应尽量平滑，以此来实现更加安全稳定的运行，而机组出力可以用等效负荷表示，等效负荷标准差SDG可以直接反应机组出力平滑程度，其具体的计算公式为

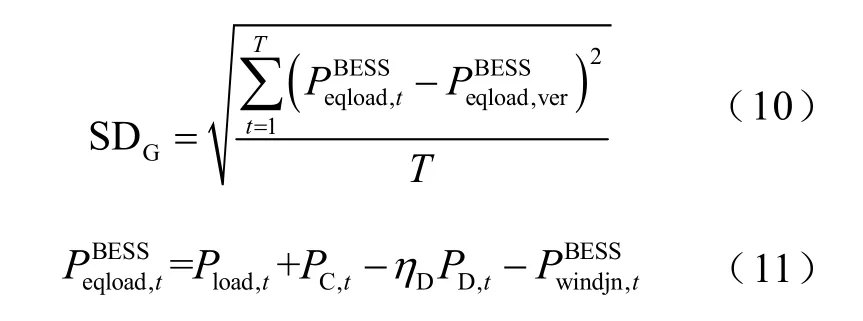
不含储能系统时的等效负荷曲线标准差为

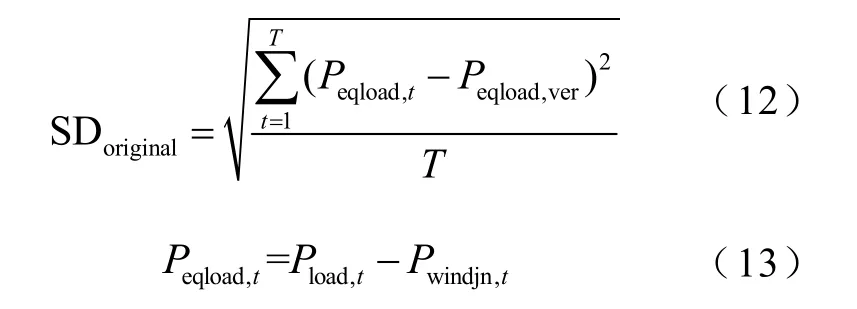
式中，Peqload,t为不含储能系统t时刻的等效负荷功率；Peqload,ver为不含储能系统的等效负荷曲线平均值；Pwindjn,t为不含储能系统t时刻的风电接纳功率。

根据上述公式建立火电机组出力标准差改善量指标为

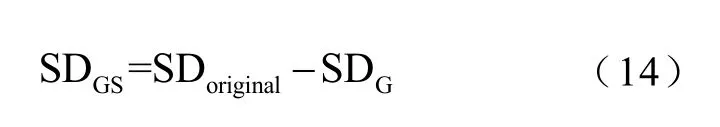
2.2.2 新增风电接纳量指标

当风电呈反调峰特性时，在负荷低谷时期弃风量大，而储能参与电网调峰可以对负荷进行削峰填谷，提升低谷时期的负荷需求，从而增加了风电接纳空间，故建立储能系统加入后的新接纳风电接纳量指标为

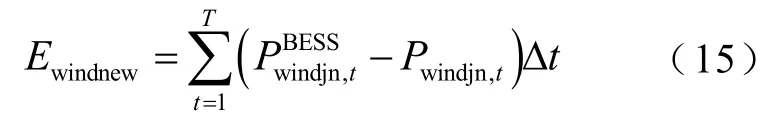
3 储能系统容量配置模型

3.1 配置方案模型结构

本文配置方案首先在外层模型中建立储能系统配置方案备选集。

其次，选取某一储能系统配置备选方案作为约束条件，根据输入的系统负荷及风电数据，在内层模型中，采用储能系统及火电机组深度调峰作用，考虑调峰过程储能系统运行成本、火电机组运行煤耗成本、火电机组深度调峰附加成本、火电机组深度补偿收益及系统风险成本因素，以系统调峰总成本最小为目标，优化系统调峰经济性，并得到该储能系统配置备选方案下的储能系统充放电功率、火电机组出力及风电接纳量。

最后，根据内层模型输出的储能系统充放电功率、火电机组出力和风电接纳量，计算储能系统各项成本收益、火电机组出力标准差和新增风电接纳量，并以储能系统全寿命周期内净收益为经济性指标，以火电机组出力标准差改善量及新增风电接纳量作为技术性指标，构成多因素优化模型，选取最优指标下对应的配置方案作为储能系统配置结果。

此外，考虑储能技术的经济性是影响储能系统发展的主要因素之一，故本文在配置方案结果的基础上，对储能系统投入运行后其全寿命周期内的经济性进行分析，并从储能技术成本单价、辅助调峰服务补偿单价和电网峰谷电价差三个角度，分析储能系统在全寿命周期内的经济平衡点。

本文所提配置模型结构如图2所示。

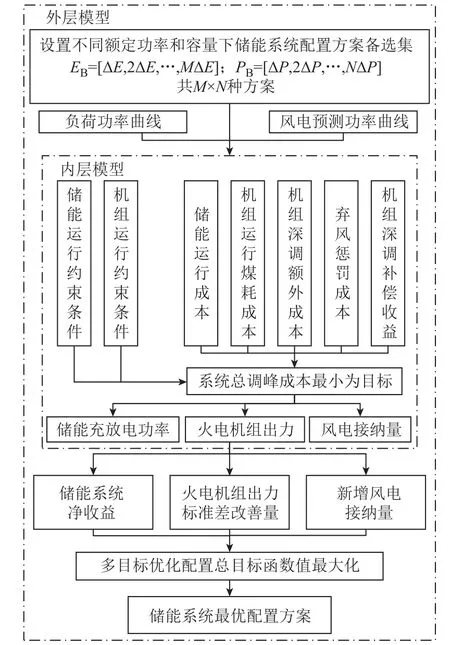
图2 储能参与电网调峰配置方案模型结构Fig.2 Structure diagram of configuration model for energy storage participating in power grid peak regulation

3.2 模型目标函数

3.2.1 外层模型目标函数

外层模型以储能系统全寿命周期内净收益、储能系统加入后火电机组出力标准差改善量以及新增风电接纳量最大为目标优化储能系统配置，其各子目标函数分别为

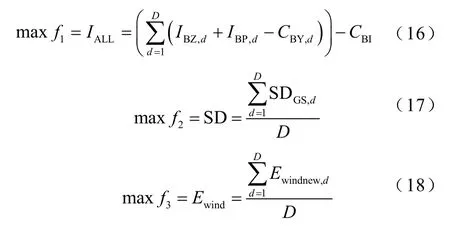
式中，IALL、SD、Ewind分别为储能系统全寿命周期内的净收益、火电机组出力标准差改善量平均值以及新增风电接纳量平均值；IBZ,d为第d天的储能套利收益；IBP,d为第d天的储能补偿收益；CBY,d为第d天的储能运行成本；CBI为储能投资成本；SDGS,d为第d天的火电机组出力标准差改善量；Ewindnew,d为第d天的新增风电接纳量；D为储能系统的总运行天数。

但在计算过程中，由于各目标量纲不同，需要对各子目标进行归一化处理。

首先对经济性目标进行标幺化。设储能系统在不同容量配置和功率配置方案下的IALL值样本集合矩阵MIALL为

式中，IALL,m,n为储能系统在容量配置为mΔE、功率配置为nΔP的条件下的IALL值。

由于在本文的经济性计算中，只考虑了储能系统的电量效益和辅助服务补偿效益，并且储能系统的成本又相对较高，所以在计算其全寿命周期内IALL值时，会出现净收益为负值的情况，所以在对其进行归一化处理时，为了避免负值的影响，将矩阵修改为

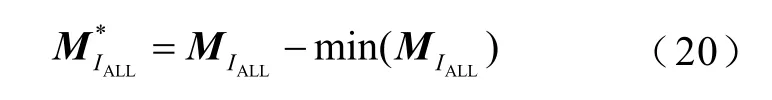
式中，min(MIALL)为MIALL矩阵最小值。

归一化后的储能系统在容量配置为mΔE、功率配置为nΔP时的IALL,m,n值为

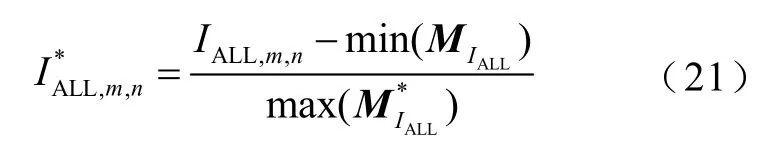
同理，对火电机组出力标准差改善量子目标以及新增风电接纳量子目标进行归一化处理，得到其在不同容量配置和功率配置下的火电机组出力标准差改善量样本集合矩阵和新增风电接纳量样本集合矩阵分别为

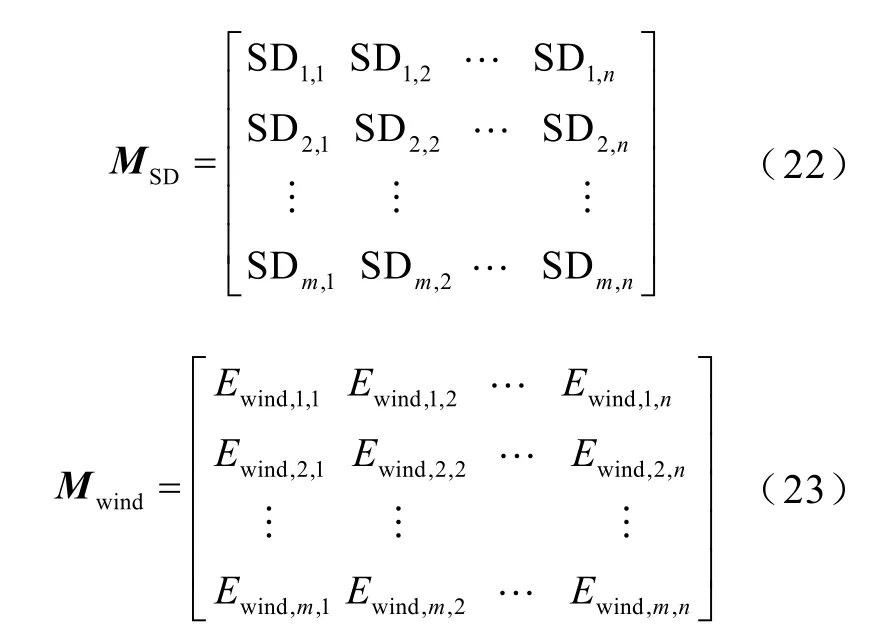
式中，MSD与Mwind分别为储能系统在不同容量配置和功率配置下的SD值样本集合矩阵及Ewind值样本集合矩阵；SDm,n与Ewind,m,n分别为储能系统在容量配置为mΔE、功率配置为nΔP的条件下的SD值与Ewind值。

归一化后的火电机组出力标准差改善量和新增风电接纳量为

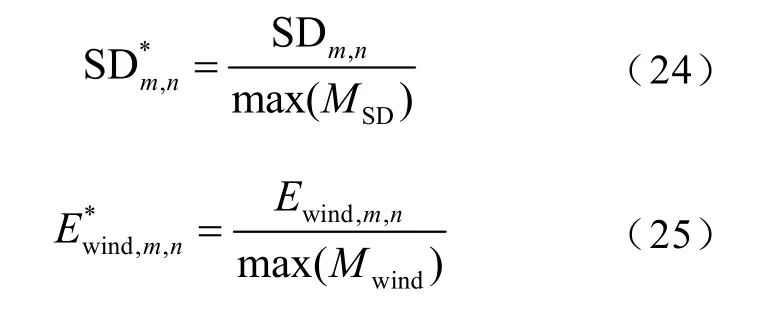
最终得到归一化后的外层模型总目标函数为

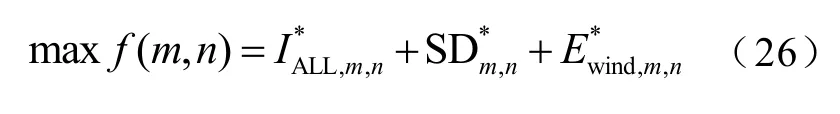
3.2.2 内层模型目标函数

内层模型考虑储能系统运行成本、火电机组运行煤耗成本、机组深度调峰附加成本和补偿收益以及弃风惩罚成本，以系统调峰总成本最低为目标，得到各储能配置方案下优化的储能系统充放电功率、火电机组出力及风电接纳量，其目标函数为

3.3 模型约束条件

3.3.1 储能系统运行约束

储能系统需满足充放电功率限值约束及荷电状态限值约束。

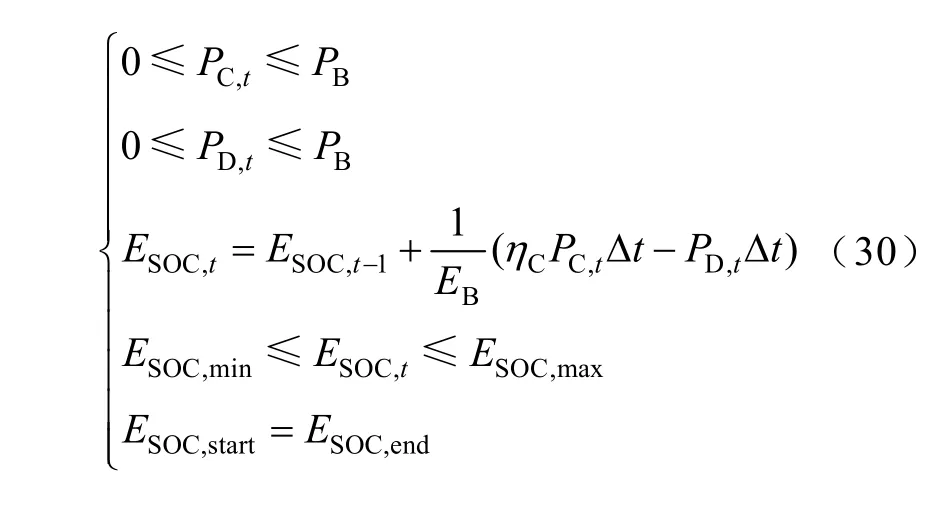
式中，ESOC,t为储能系统荷电状态；EB为储能系统额定容量；ESOC,max与ESOC,min分别为储能系统荷电状态上、下限值；ESOC,start为初始时刻储能系统荷电状态；ESOC,end为末尾时刻储能系统荷电状态。

3.3.2 火电机组运行约束

火电机组需满足火电机组的功率上下限约束、爬坡率约束和起停约束。

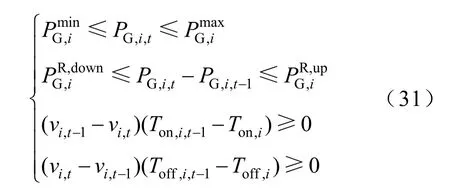
3.4 模型求解方法

1）外层模型求解方法

在外层多目标优化配置模型中，首先以 ΔE及ΔP为储能系统的容量及功率配置基本单位，设置储能系统容量备选集{ΔE,2ΔE,…,MΔE} 及储能系统功率备选集{ΔP,2ΔP,… ,NΔP}，从而形成M×N种备选方案。以迭代法计算每种方案下的多目标函数值，选取最优值对应的配置方案为储能系统配置结果，其求解流程如图3所示。

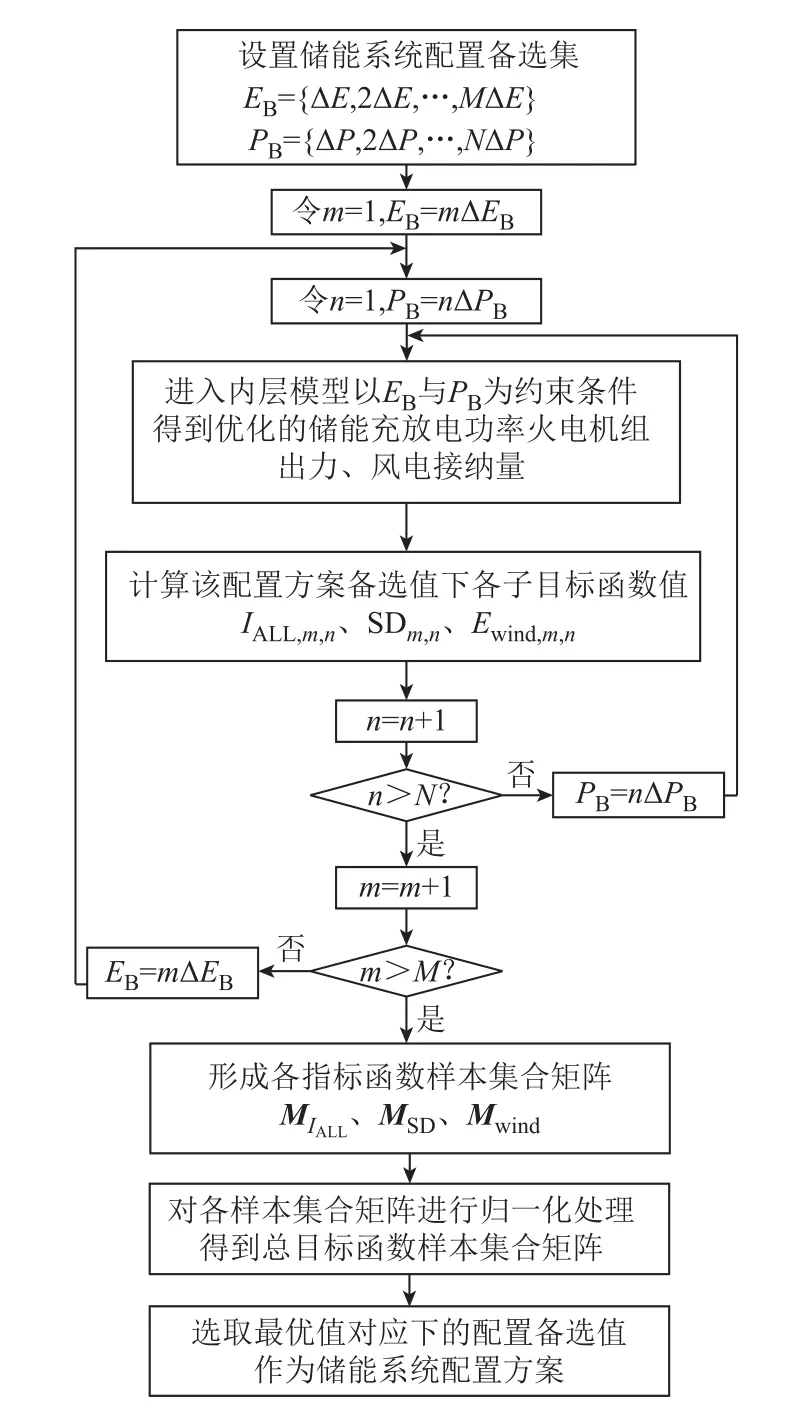
图3 外层配置模型求解流程Fig.3 Solution flow chart of outer configuration model

2）内层模型求解方法

在内层储能辅助火电机组调峰优化调度模型中采用Matlab中的CPLEX求解器求解，从而得到不同储能系统配置备选值下的储能充放电功率、火电机组出力及风电接纳量。

4 算例分析

4.1 算例参数

1）储能系统参数设置本节算例将储能系统安装于电网发电侧，并选用已有大规模应用的磷酸铁锂电池及全钒液流电池，其参数见表1[29]。

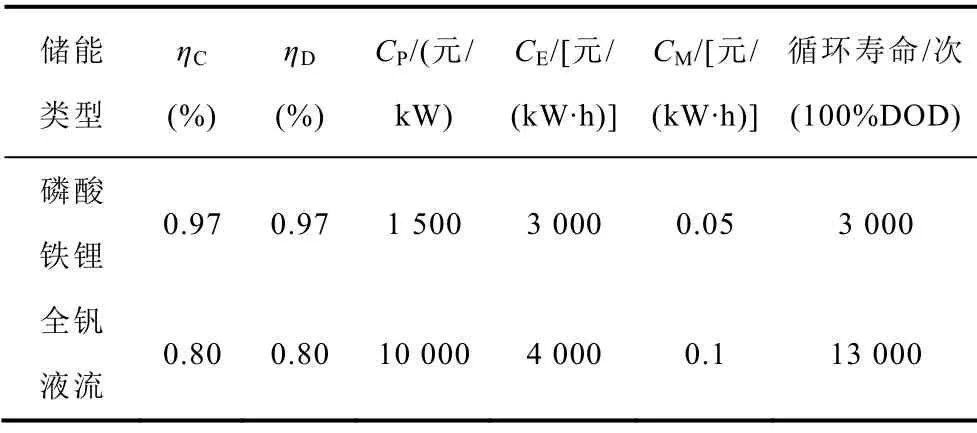
表1 储能系统参数表Tab.1 Parameter table of energy storage system

根据表1中数据可知，磷酸铁电池的运行年限NZ为8.2年，全钒液流电池的运行年限NZ为35.6年。

储能系统套利收益根据该地区的峰谷电价实现，其各时段的峰谷电价见表2。

表2 某地区峰谷电价参数表Tab.2 Parameter table of peak-valley electricity price in a certain area

该地区目前没有明确的储能调峰补偿政策，故先设置Pcom=0元/(kW·h)；设储能系统荷电状态限值为0.1～0.9；折现率rs=0.04；弃风惩罚系数θ=0.61元/(kW·h)。

2）火电机组参数设置

选用某局部电网数据进行分析，该电网火电机组总装机容量3 200MW，各机组参数见表3[30]。

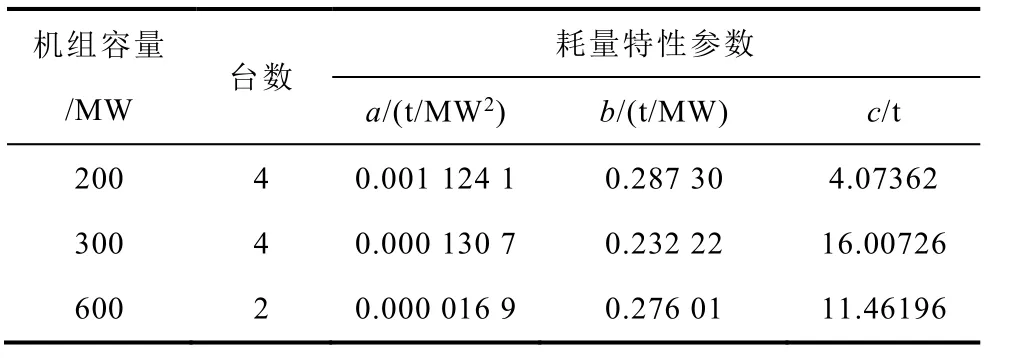
表3 火电机组参数表Tab.3 Parameter table of thermal power unit

机组锅炉燃料为焦煤，价格为685元/t；弃风惩罚成本为0.61元/(kW⋅h)[30]。

算例中，设200MW与300MW机组只进行基础调峰，其基础调峰阶段的最低负荷率为50%。设600MW机组参与深度调峰，其在深度调峰时的相关参数如下[23]：

（1）机组基础调峰阶段的最低负荷率为50%，不投油深度调峰阶段的最低负荷率为40%，投油深度调峰阶段的最低负荷率为30%。

（2）不投油深度调峰阶段的运行损耗系数β=1.2，投油深度调峰阶段的运行损耗系数β=1.5。

（3）机组单位造价成本3 464元/kW。

（4）在深度调峰阶段的转子致裂周次N与机组功率P的关系式为N(P)=0.005778P3-2.682P2+484.8P-8411。

（5）机组在投油深度调峰阶段的油耗量为4.8t/h，油价为6 130元/t。

（6）根据《东北电力辅助服务市场运营规则（试行）》中的相关规定，设定火电机组参与深度调峰的补偿电价为0.4元/(kW⋅h)。

此外由于本文研究主要满足系统的有功功率平衡，未考虑电网网架结构的影响。

3）仿真数据

本算例采用该区域电网七天的风电功率数据和负荷功率数据进行仿真，如图4所示。

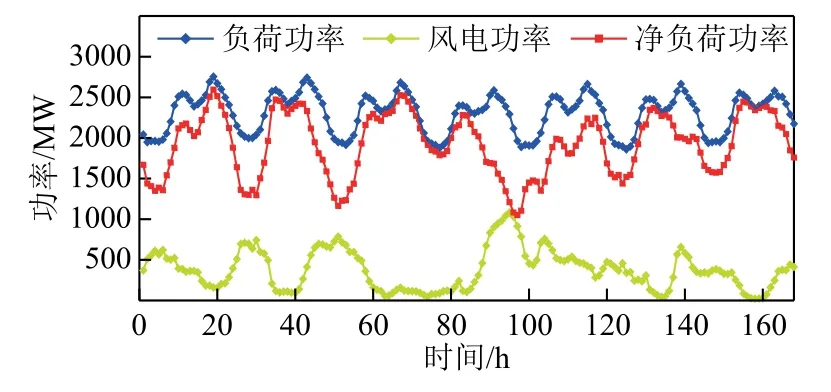
图4 七天风电与负荷数据Fig.4 Wind and load data for seven days

4.2 算例及分析

1）内层优化调度策略算例分析

首先采用磷酸铁锂电池对内层优化调度策略的有效性进行分析，设磷酸铁锂电池储能系统配置方案为200MW/800MW·h（目前国内最大配置的储能系统工程项目[31]）。

经内层优化调度策略后的储能系统充放电功率，储能荷电状态，各火电机组出力以及风电接纳量如图5及图6所示。

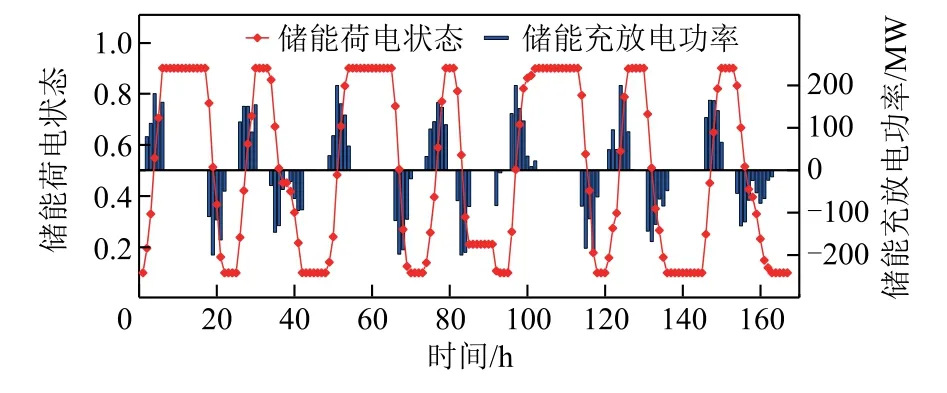
图5 储能系统充放电功率及荷电状态Fig.5 Charge and discharge power and state of charge of energy storage system

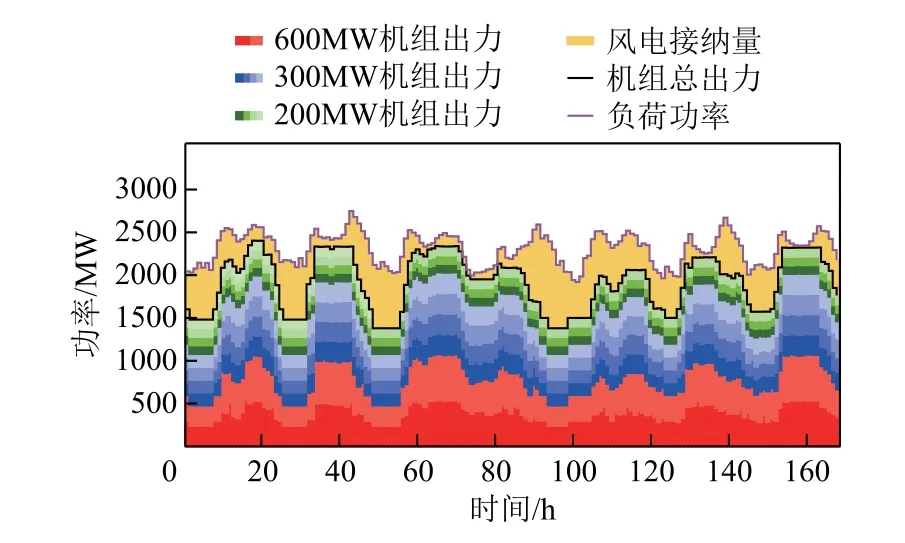
图6 各机组出力及风电接纳功率累加图Fig.6 Accumulation chart of unit output and wind power acceptance power

从图5中可以看出，储能系统各时刻的充放电功率最大值均为200MW，都在额定功率范围之内，并且荷电状态也始终保持在限制值范围0.1～0.9之内，说明本文所提的储能调度策略可以很好地满足储能系统的约束条件。

再结合图6可以看出，储能系统通过在负荷低谷及高峰时期的合理充放电，使得火电机组在负荷低谷及高峰时期的出力曲线更加平滑，可以使机组更加安全稳定运行，并且减少机组日出力调节量。

为了对本文内层调度策略进行对比分析，分别设置三种不同的调峰调度方案：①火电机组基础调峰；②火电机组深度调峰；③储能加火电机组深度调峰。各方案优化结果见表4。

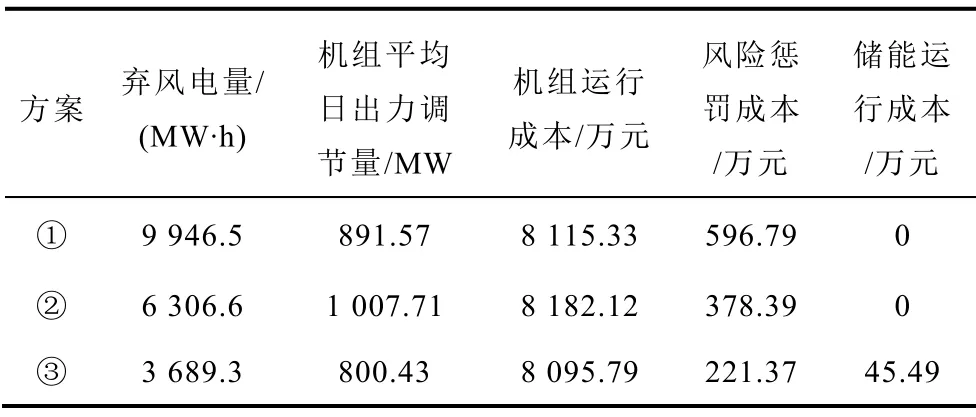
表4 不同方案调峰效果及经济性对比Tab.4 Peak shaving effect and economic comparison of different schemes

在火电机组进行深度调峰时，对比方案①其弃风电量减少3 639.9MW·h，降幅为36.59%。但是由于深度调峰，故在负荷低谷时期的机组出力值较低，故机组的日出力调节量有所上升。

而采用储能辅助火电机组深度调峰调度策略时，弃风电量得到明显的改善，相较于方案①下降6 257.2MW·h，降幅为62.90%，相较于方案②下降2 617.3MW·h，降幅为41.50%。此外，储能系统的削峰填谷作用等效减小了机组日出力调节量。从表4中可知，方案③较方案①的机组日出力调节量降低91.14MW，较方案②的机组日出力调节量降低207.28MW。

此外，从系统调峰经济性角度分析，火电机组深度调峰会额外产生高昂的损耗成本和投油成本，故提高了机组运行成本，但减少了弃风惩罚成本，故方案②的总调峰成本比方案①降低了151.61万元。

而储能系统加入后，缓解了机组深度调峰压力，并且降低了负荷高峰时期的机组出力，在降低机组运行成本的同时大幅降低弃风惩罚成本，方案③的系统总调峰成本较方案②降低197.86万元，较方案①减少349.47万元。

通过上述分析可知，储能辅助火电机组深度调峰在系统调峰效果及系统调峰经济性方面都具有一定的优势。

2）外层优化配置策略算例分析

基于有效的内层优化调度策略，再对外层优化配置策略进行分析。设置储能系统功率配置备选集为0～200MW，迭代步长ΔP=5MW；容量配置备选集为0～800MW·h，迭代步长ΔE=5MW·h。储能系统备选集范围按照国内目前最大储能工程项目选定[31]。则两种储能系统在各配置方案下的总目标函数值三维曲面图如图7和图8所示。

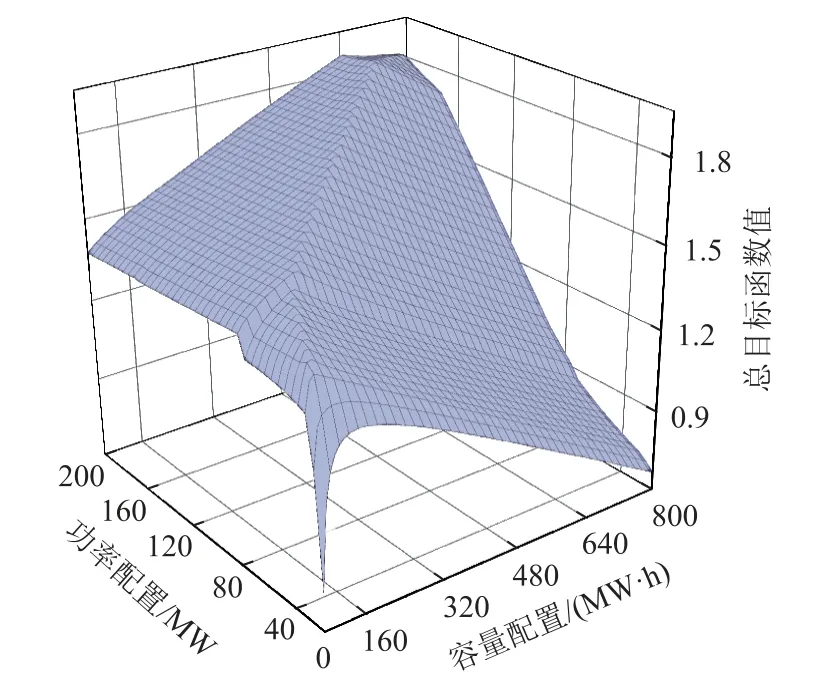
图7 磷酸铁锂电池优化配置总目标函数值三维曲面图Fig.7 Three-dimensional surface plot of the total objective function value of the optimal configuration of lithium iron phosphate battery

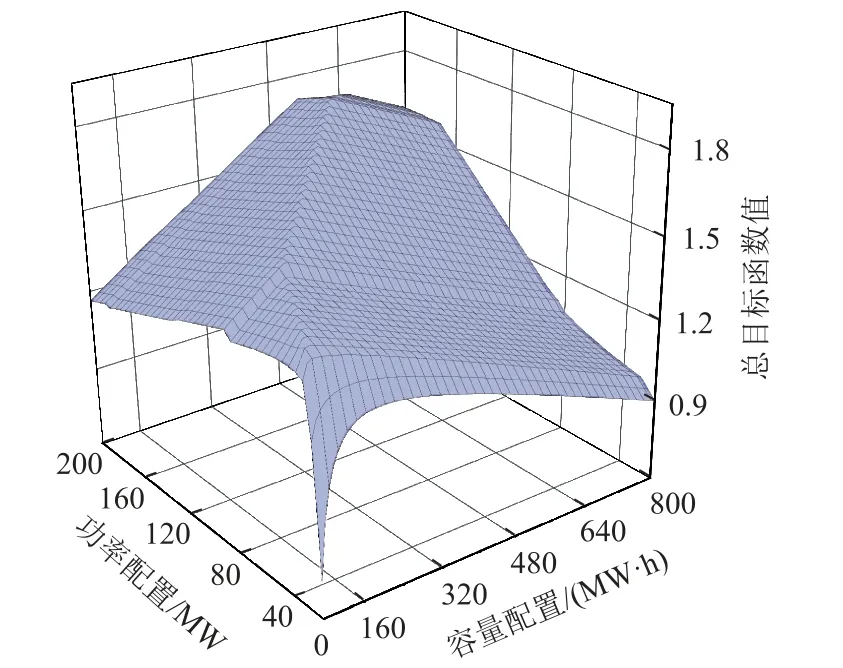
图8 全钒液流电池优化配置总目标函数值三维曲面图Fig.8 Three-dimensional surface plot of the total objective function value of the optimal configuration of full vanadium flow battery

两种储能系统在最优总目标函数值下对应的储能系统优化配置方案、全寿命周期经济性、火电机组出力标准差平均值以及风电接纳量平均值见表5。

从表5中数据可以看出，在最优配置下各储能系统的调峰效果水平非常接近，但对应的配置结果却有所差异。由于全钒液流电池的充放电效率较低，故在相同调峰效果下，损耗的电量较多，所以其容量优化配置结果较小。

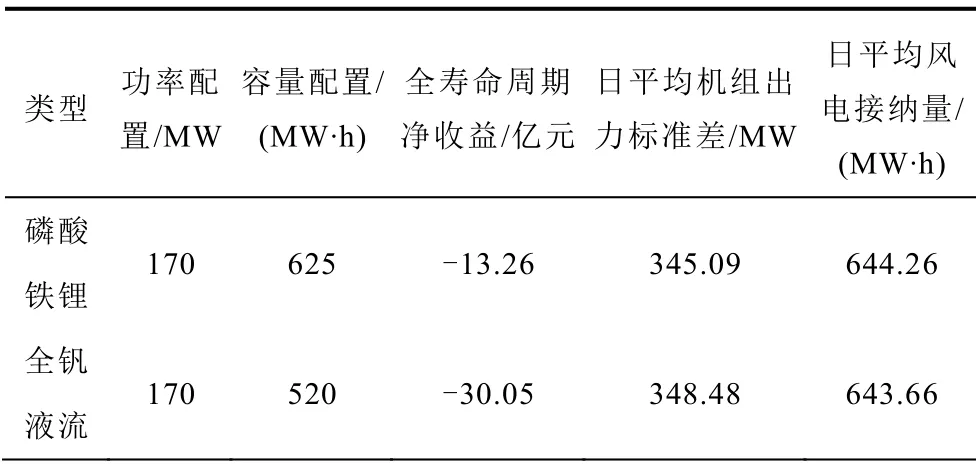
表5 两种储能系统最优配置方案及其对应调峰参数Tab.5 Optimal configuration schemes of two energy storage systems and their corresponding peak shaving parameters

而从经济性角度可以看出，由于本文在对于储能系统全寿命内的经济性计算时，只考虑了储能系统的直接经济性指标，所以两种储能系统的亏损情况较为严重，可见目前储能系统的经济性仍是阻碍其发展的主要因素之一。

下面从储能系统辅助服务补偿单价、峰谷电价差以及储能系统自身成本角度出发，分析储能系统达到经济平衡点。

图9为在补偿电价及峰谷电价递增下的磷酸铁锂电池全寿命周期内净收益热点图。随着补偿单价及峰谷电价差的提高，储能系统的经济性也不断提高。图中白色区域为磷酸铁锂电池接近经济平衡点时所需的补偿单价及峰谷电价差解集。从图9中可知，通过增加补偿单价或增加电网峰谷电价差来实现磷酸铁锂电池的经济平衡有一定的可行性。通过图中数据分析可知，单独增加补偿电价来达到经济平衡所需价格为0.46元/kW；单独增加峰谷电价差来达到经济平衡所需电价差为1.99元/kW，为现有电价差的2.55倍。

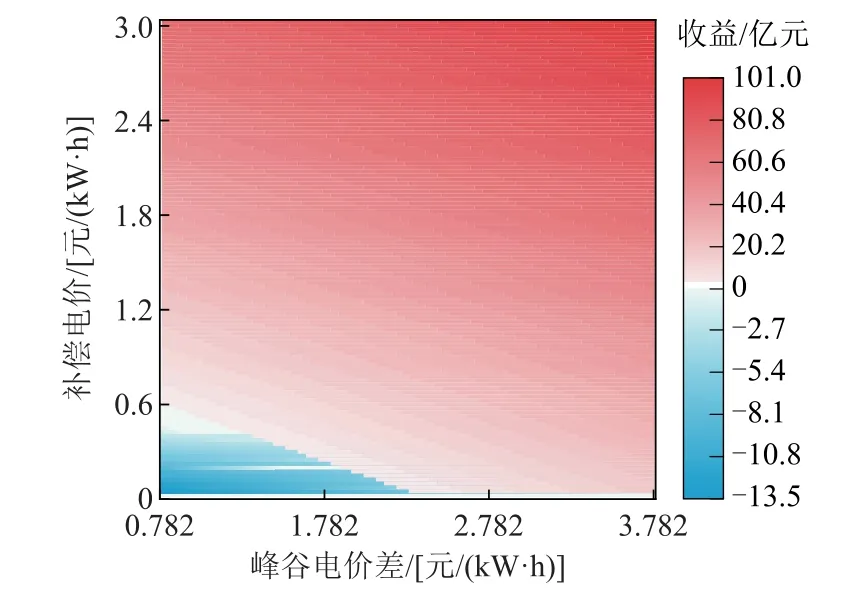
图9 随补偿电价和峰谷电价差递增的磷酸铁锂电池净收益变化热点图Fig.9 Heat map of changes in net income of lithium iron phosphate battery with increasing compensation price and peak-to-valley price difference

图10为在储能功率成本单价及容量成本单价递减下的磷酸铁锂电池全寿命周期内净收益热点图。随着储能系统功率单价及容量单价的递减，磷酸铁锂电池储能系统全寿命周期内的净收益热点越高，其经济性越好。图中白色区域为磷酸铁锂电池接近经济平衡点时所需的容量单价及功率单价解集。从图中可知，通过降低容量单价及功率单价来实现经济平衡还有一定的难度，所需的价格离目前单价还有一定距离。根据图中数据分析可知，单独减小容量价格来达到经济平衡所需价格为745元/(kW·h)，降低幅度为75.16%；而单独减小功率单价却无法达到经济平衡。

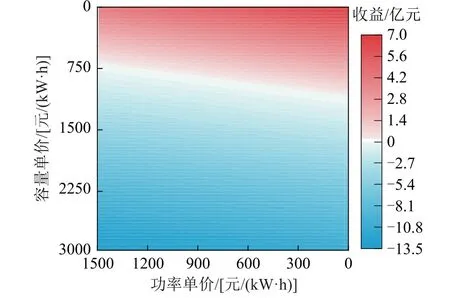
图10 随容量单价和功率单价递减的磷酸铁锂电池净收益变化热点图Fig.10 Heat map of changes in net income of lithium iron phosphate battery with decreasing capacity unit price and power unit price

图11为在补偿电价及峰谷电价递增下的全钒液流电池全寿命周期内净收益热点图。随着补偿单价及峰谷电价差的提高，储能系统的经济性也不断提高。图中白色区域为全钒液流电池接近经济平衡点时所需的补偿单价及峰谷电价差解集。从图11中可知，通过增加补偿单价或增加电网峰谷电价差来实现全钒液流电池的经济平衡有一定的可行性。根据图中数据分析，单独增加补偿电价来达到经济平衡所需价格为0.45元/kW；单独增加峰谷电价差来达到经济平衡所需电价差为2.29元/kW，为现有电价差的2.93倍。

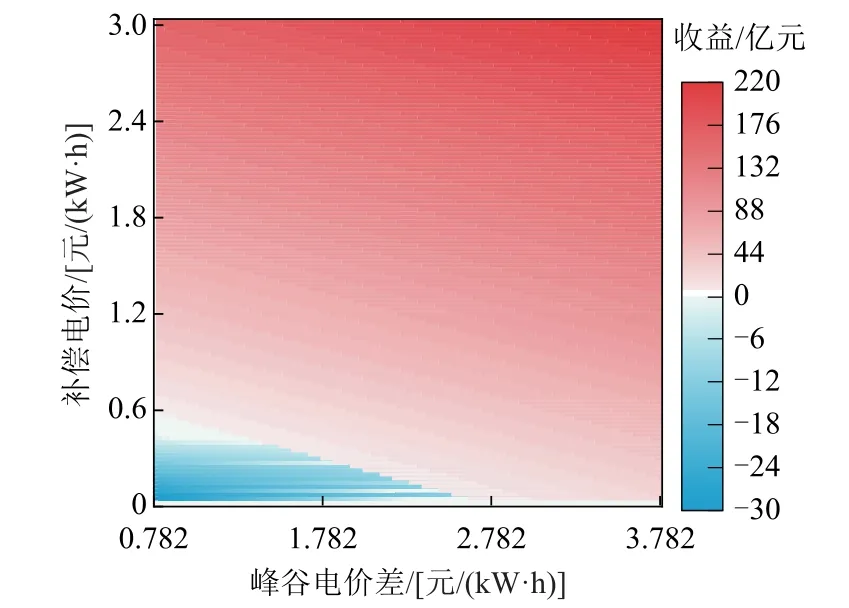
图11 随补偿电价和峰谷电价差递增的全钒液流电池净收益变化热点图Fig.11 Heat map of changes in net income of full vanadium flow battery with increasing compensation price and peak-to-valley price difference

图12为在储能功率成本单价及容量成本单价递减下的全钒液流电池全寿命周期内净收益热点图，随着储能系统功率单价及容量单价的递减，全钒液流电池储能系统全寿命周期内的净收益热点越高，其经济性越好。图中白色区域为全钒液流电池接近经济平衡点时所需的容量单价及功率单价解集。从图中可知，通过降低容量单价及功率单价来实现经济平衡也存在一定的难度，所需的价格离目前单价还有一定距离。根据图中数据分析可知，单独减小容量价格及功率价格均无法达到经济平衡。

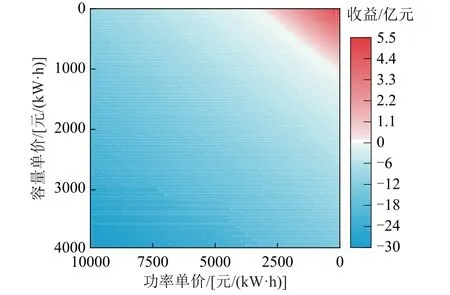
图12 随容量单价和功率单价递减的全钒液流电池净收益变化热点图Fig.12 Heat map of changes in net income of full vanadium flow battery with decreasing capacity unit price and power unit price

通过上述分析，使储能系统达到经济平衡点最有效的方式为提供相应的辅助服务补偿。但上述分析只是从单方面的价格变动来达到经济平衡点，未来随着政策的完善以及储能系统自身成本的降低，储能系统的经济性将得到极大的改善。

5 结论

针对火电为主东北地区风电高渗透电网的调峰问题，提出一种参与电网调峰的储能双层优化配置策略，并对储能系统进行经济性分析，主要结论如下：

1）以配置200MW/800MW·h磷酸铁锂电池储能系统为例，本文调度策略可以降低62.90%的弃风功率，降低347.47万元系统总调峰运行成本。

2）在负荷功率水平为2 800MW左右，风电渗透率约40%的电网中，磷酸铁锂储能系统最优配置结果为170MW/630MW·h，全钒液流储能系统最优配置结果为170MW/520MW·h。

3）在优化配置结果的前提下，当补偿单价在0.46元/(kW·h)，峰谷电价差为1.99元/(kW·h)，容量价格为745元/(kW·h)时，可使磷酸铁锂电池储能系统达到经济平衡。

4）在优化配置结果的前提下，当补偿单价在0.45元/(kW·h)，峰谷电价差为2.29元/(kW·h)时，可以使全钒液流电池储能系统达到经济平衡。

由于本文研究对象针对东北电网，传统电源中主要计及火电机组，对于富含水电区域的可再生能源大规模接入带来的调峰问题，本文容量配置模型的适应性还有待进一步研究。