基于机器学习的可转债定价与实证分析研究

牛晓健 巴雄

摘要：可转换债券作为一种兼具债券和股票特征的金融产品，已成为资本市场重要的融资工具和广大投资者青睐的资产配置工具。由于国内可转债的附加条款及内含期权复杂，常用的Black-Scholes公式严格的前提假设往往造成定价结果偏差较大。经实证发现，以31个可转债因子作为解释变量，通过支持向量回归能很好地拟合可转债价格。

关键词：可转债定价;Black-Scholes模型;机器学习;支持向量回归

中图分类号：F832 文献标识码：A文章编号：1009 - 5381（2021）05 - 0058- 14

收稿日期：2021 - 08 - 02

基金项目：本文系国家自然科学基金面上项目“流动性压力、信息交互与价格联动——基于中国股票和债券市场多层复杂网络的风险交叉

传播机制与控制修复策略研究”（项目批准号：71873039，71573051）阶段性研究成果。

作者简介：牛晓健，男，新疆阿克苏人，复旦大学国际金融系教授。研究方向：量化投资。

巴雄，男，江西九江人，复旦大学经济学院金融硕士研究生。研究方向：量化投资。

一、引言

可转换公司债券（以下简称可转债）是指持有者可在规定时间内按照转股价转换为公司股票的债券，或者可以直接持有到期等待发行人还本付息。可转债最早出現在美国金融市场，由于兼具债券价值的保底和复杂期权的波动机会，可转债在发达的金融市场发展迅速。中国的可转债市场起步较晚，发展历程大致可以分为几个阶段： 第一个阶段是21世纪之前。1993年，国内可转债市场迎来了首个可转债标的——由中国宝安集团发行的宝安转债，发行规模为5个亿。1997年，国务院证券委员会发布《可转换公司债券管理暂行办法》，这个阶段是我国对可转债的初步探索。第二个阶段是2000-2004年。这期间相继迎来了《上市公司发行可转换债券的实施办法》《关于做好上市公司可转换债券发行工作的通知》两大规范政策，市场上的可转债标的数量达到两位数，可转债市场异军突起。第三个阶段是2005-2016年。这期间我国可转债市场经历了2005年的股权分置改革的一级市场停滞，随后又逐渐恢复繁荣。在2015年股灾期间，出现大幅赎回及发行停滞的现象，可转债市场大起大落，规模尚小。第四个阶段是2017年至今。2017年，国家进一步严格股票定向增发的要求，可转债市场诸多利好政策出现，可转债发行数量和发行规模大幅增加。近些年来，为解决中国再融资的结构失衡，监管层进一步完善了可转债、可交换债的发行方式，为可转债等再融资产品创造了良好的发展条件。

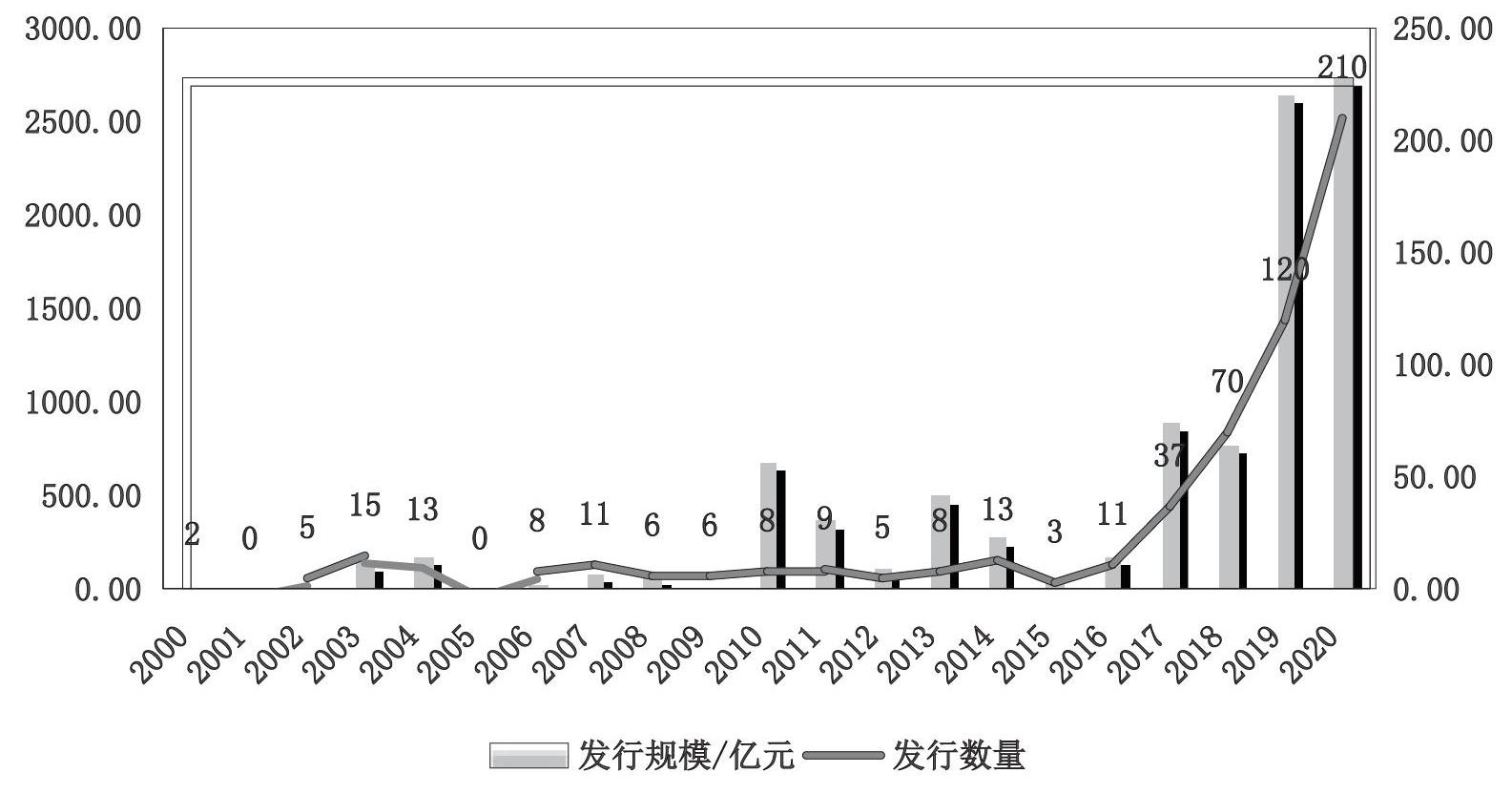
从图1可以清晰看出2000年至今可转债市场的变化，即随着我国可转债发行数量的增加，可转债市场发行规模逐渐增加。其中，2019年发行规模2657亿，2020年发行规模2736亿，2020年发行数量210只。与此同时，可转债存量达5434亿。截至2021年3月19日，可转债数量达374只。

图1  2000-2020年中国可转债的发行情况

无论是从可转债发行数量还是从发行规模来看，可转债市场都已经进入快速发展阶段，但由于可转债条款设计的复杂性，加上投资者知识匮乏，导致可转债暴涨暴跌及可转债折价现象频发，不利于我国可转债市场的健康发展。因此，解决可转债定价效率低的问题成为重中之重。一方面，合理的定价体系可以让发行人有效地发行可转债，制定内含的各种条款，寻找最优的融资方式;另一方面，正确的定价体系能帮助投资者准确地对可转债价格进行估计，构建最优的投资组合。可转债定价方法的探索不仅要借鉴国外经典的可转债定价思想，更要从我国可转债市场的特点出发，与时俱进，尝试从更多历史数据中挖掘对可转债价格具有解释力的信息。目前机器学习方法在国内金融市场中已有较多应用，且随着可转换债券投资性价比逐步提升，机器学习模型在可转债定价领域更具可行性。

二、文献综述

（一）国外可转债定价方法综述

国外对可转债定价的研究首次出现于1968年[1]，Weil以及后来的Baumol and Malkiel 等对可转债的价格属性展开讨论，将可转债的价格等价为未来选择转股后的股权价值，以及作为信用债持有到期的价值两部分并进行贴现，取较高者作为当前转债的合理定价。

其中BC为转债价值，B为未来时点的信用债价值，S为未来时点的选择转股获得的股权价值，r为折现率，t为未来时点距离当前的时间。

1970年，Black-Scholes期权定价公式的诞生使可转债的相关研究开启了新的篇章，模型认为可转债价值包含了公司债券和若干份股票期权两种金融工具的价值。B指的是可转债的纯债价值，OP是转股期权的价值，B为每期现金流贴现之和，其中为每期现金流，为信用价差，为无风险利率。OP由Black-Scholes公式算得，其中K为转股价格，股价历史波动率为δ，可转债期限为T：

Brennan and Schwartz[2]认为，可转债价值只由服从几何布朗运动的公司市场价值决定，从而基于Black-Scholes公式和风险中性定价思想，推导出偏微分方程，结合最优赎回策略和最优转换策略确定微分方程的边界条件求解。Ho and Pfeffer[3]在定价中引入了利率的波动。Goldman Sachs[4]首次将可转债的信用风险引入定价模型，综合股价的波动与信用风险的调整给出可转债定价方法。Longstaff and Schwartz[5]提出了最小二乘蒙特卡罗模拟法（Least Squares Monte Carlo Simulation，简称LSM），该方法假设正股未来波动符合几何布朗运动，在模拟生成大量可能的正股价格序列后，便可以采取类似于二叉树的逆向推导方法，借助最小二乘估计逐步推算前一期转债的期望持有价值，最后对各条模拟路径的转债估值结果取平均值，从而得到转债在当前时点的理论定价。Dubrov and Bella[6]曾提出强化学习算法可以比蒙特卡洛模拟更好地找到最优执行策略，基于大量的实证研究和数值实验，发现若引入二叉树的计算，机器学习模型将更有效。

（二）国内可转债定价方法综述

自从我国第一只转债（宝安转债）上市后，国内开始出现可转债定价的实证分析。具有代表性的为郑振龙教授在2004年提出的风险中性定价法，通过赎回条款及转换条款确定边界条件，通过数值解法解得可转债价格。郑振龙、林海[7]率先指出，可转债的定价复杂性主要表现在是否执行期权以及何时执行期权，由此产生的问题可以歸纳为：

1.附加条款的期权为奇异期权，很难得到其解析解;

2.转股期权为美式期权，很难以蒙特卡洛模拟;

3.内含期权多为路径依赖期权，难以使用二叉树和有限差分法等数值方法。

如图2所述，可转换债券的价值由股票价格和债券价值决定，假设股票价格服从几何布朗运动：

可转债视为股票的衍生品，可转债的价格偏微分方程可表示为：

江良、林鸿熙、林建伟及宋丽平[8]基于随机利率模型对可转换债券定价分析，结果显示利率的随机波动对可转债价值具有影响。王茵田、文志瑛[9]基于Tsiveriotisand Fernandes信用风险的定价模型，发现考虑修正条款后，模型的精度明显提高且可转债溢价现象有所改善。马林、黄中翔[10]采用偏最小二乘回归方法，选取了对可转债具有解释能力的变量，并分类为转债、正股及指数类因子，结合最优停时定理给期权定价。程志富、胡昌生[11]构建了基于套利限制的可转债交换期权模型，基于远期风险中性测度以及期权的超复制方法，并应用2015年2月至10月的可转债数据进行验证，提升了模型准确度。沈传河等[12]基于改进的支持向量回归算法，以钢钒转债为例，考虑了诸如正股价格、转股溢价率等8个相关变量，进行支持向量回归SVR训练，并对203条数据进行测试，发现支持向量回归模型的准确度最好。

以往文献采纳的定价框架大都基于严格的Black-Scholes公式前提假设，然而这些假设是我国金融市场无法满足的。随着机器学习模型的流行，机器学习模型的强大拟合能力以及函数优化的特征被慢慢挖掘，加之不断充实的数据为模型提供了较强的支撑，使得模型精度及稳定性进一步提升。下文将尝试用机器学习拟合的方法给可转债定价。

三、可转债价格影响因子及有效性检验

（一）可转债价格影响因子

如图3所示，当正股股价较低或平价小于面值100的状态，可转债价格贴近于债底价值小幅波动;当正股股价较高或平价大于面值100的状态，可转债价格贴近于平价或者转股价值波动。其中，可转债价格相对于债底或平价的溢价通常被解释为转债的估值变动。

价值分解也可以进一步用Black-Scholes公式求导来说明，可转债价值CB同时由债底B、正股S及估值Vol驱动。在我国，还由可转债的自身特有属性决定（如附加条款等）。

我国可转债市场的波动更多由可转换债券对应正股的价值主导。对比2007年1月至2020年12月间中证转债指数和沪深300指数净值曲线，两者波动方向基本一致，说明转债涨幅主要依赖于对应正股的驱动力，见图4。

在我国转债市场内，由于几乎无法低成本对冲，可转债的价值根本在于正股，转债大多以转股的方式退出转债市场。此外，虽然债底价值占据大部分的比例，但带来的波动却是股远大于债。因此，正股类驱动力实证部分重点关注转债对应正股的营收能力、盈利能力、现金流情况及资产负债结构，同时也应综合考虑对应正股的规模、估值及所处的行业等因素。

债底价值在可转债价值中占比较大，但纯债价值的波动对于可转债价值的影响较小。一是国内可转债的面值接近纯债价值;二是若债底价值因出现了利好而明显上升，机会成本增加，投资者不会因此去投资可转债。

本文从债底价值计算公式出发，考虑票面利率、债券面值、贴现率、补偿利率及现金流贴现率，应用可转债评级对应同时期中债企业债收益率作为分母的现金流贴现率。

转债价格相对于其债底价值和转股价值的溢价被投资者称为可转债的估值，实际投资中常用纯债溢价率和转股溢价率来衡量。估值指标大小也决定了可转债是偏股性还是偏债性。本文采取转股溢价率及纯债溢价率两类指标分别衡量转债的股性和债性。

自身属性和附加条款类因子，主要考虑可转债是否进入了赎回、回售期，这点可从公司发布的强制赎回或强制回售公告中获取，是否进入了下修期能从可转债规定的转股价格来反映。自身属性主要从债性评级、中签率、所处生命周期等因子来考虑。

本文从可转债的正股影响因素、债底计算公式、估值因子及附加条款归纳总结了对转债价格有解释力的31个因子，如表1所示。经过因子数据的去极值及标准化处理后，对因子进行分层回测检验。各部分因子在后续实证过程中都统一为日频，未更新的日期采用最新的数据填充。数据均可从Wind获得，缺失率不高，因子覆盖度较好。

（二）因子分层回测及检验

分层检验常用于股票多因子策略中因子有效性的检验部分，目的是通过在每一个横截面将不同因子的截面数据进行分层。如果不同层因子的表现有显著区别，则证明该因子对转债的收益率具有解释力度。具体操作步骤如下：

1.选取2019年1月-2020年11月期间有交易数据的可转债标的，一共85只可转债标的和433个交易日数据;

2.因子每一周按数值从小到大排列分成五层，在这一周内分别持有排列在每一层的转债，设置交易费用万分之三，下一周按此规则换仓;

3.在区间内每周换手一次，最后得到每层的一个收益率序列，并画出每层转债的累积收益率曲线。

需要说明的是，因子的表现可能在某些时段分层效果较好，有些时段分层不显著。该现象可能由可转债市场风格变动等原因导致，我们认为这类因子对价格仍具有一定解释力度。另外，由于截面数据量较少，容易出现单层数据少，可能给分层结果带来偏差。

如图5所示，转股溢价率因子在测试区间段内分层效果较明显，反映出转股溢价率是一个不错的估值因子，回测区间内呈现较好的单调性。低转股溢价率的转债累积收益率越高，一定程度上印证了可转债的低价格低溢价率策略，即“双低”策略在我国转债市场投资中表现较好。

图6中，隐含波动率因子分层效果较为理想，意味着通过隐含波动率来挑选可转债，长期看来具有一定的穩定性和正向收益。隐含波动率的单调性表现较好。

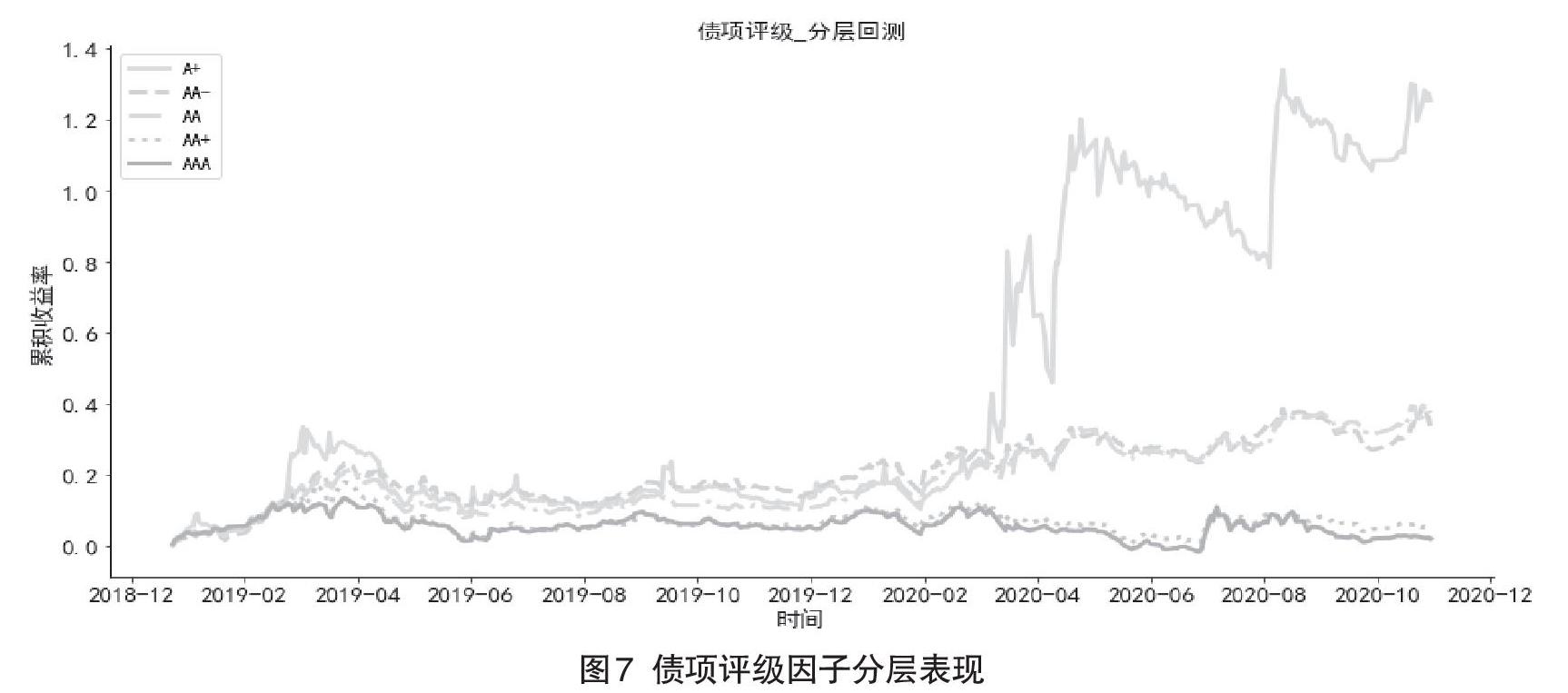
图7中，可转债的债项评级效果也较好，高评级债券累计收益率波动更小，收益也相对较低。相对来说，低评级债券展现出更大的波动，也有更高的收益。这是因为低评级债券的正股虽然市值小，但弹性更大，且低评级的转债规模也相对更小，更容易出现弹性更大的情况，所以在2019年和2020年大盘环境好的时候，容易出现价格迅速上升的现象。

图8中，可转债的对应正股股价日波动率分层明显且单调性较好，表明正股波动率越大，可转债累积收益越高，这在2020年表现尤为明显。这也印证了波动率越高、可转债的内含期权价值就越大、可转债价值越高的这一规律

四、机器学习介绍及支持向量机理论

（一）机器学习模型定价优势

从可获取的可转债历史数据的宽度及深度、定价模型的优劣及模型的假设条件来看，应用机器学习模型的优势在于：

1. 我国的可转债市场在存量和增量上，目前均有足够历史数据支持机器学习模型的训练和验证。同时，随着机器学习理论的不断深化应用，国内外开始出现基于复杂的数学模型给转债定价的实证分析。未来我国可转债市场有效性有望增强，一些转债交易乱象产生的数据噪声也将逐渐变少。

2. 现有的可转债定价理论大多基于Black-Scholes框架，考虑的因素多为Black-Scholes公式中的影响因素，比如股价、波动率、利率及执行价格（转股价格），未考虑估值因子（转股溢价率等）和正股的基本面表现。

3. 我国金融市场不满足Black-Scholes理论中股价符合几何布朗运动以及期权可对冲复制的两点假设，且市场卖空机制还有待完善，造成Black-Scholes定价结果的偏差。相比之下，支持向量机回归模型不需要局限于这些假设，更多的是通过对输入的解释变量和被解释变量关系的训练，找出之间的函数关系。不可忽略的是，通过支持向量机回归（SVR）模型难以计算出衡量可转债内含期权的敏感性的字母，而这正是Black-Scholes模型的理论优势所在。

（二）支持向量机理论

支持向量机SVM（Support Vector Machine）是一个数学理论严格完备的模型，可以用来解决分类问题（Support Vector Classify）和回归问题（Support Vector Regression）。支持向量机有较高的拟合准确率，在非线性、小样本及高维模式方面都具有比较明显的优势，常用来解决非线性分类问题及回归问题，通过改变核函数及其参数可以调试不同的预测效果，是目前应用最广泛的机器学习方法之一。本文主要介绍实证过程中涉及的支持向量机回归的思想及解法。

机器学习模型与普通最小二乘线性回归方法最大的区别就是损失函数。只有在输出结果与真实数据之间的差距超过一定值ε时，机器学习模型才会计算损失，并给予对应的惩罚系数。

如图9所示，如果训练样本的输出结果满足时，是实际结果，则认为输出结果没有损失;如果训练样本的输出结果满时，则需要计算模型的损失并给予惩罚。进而，支持向量机回归问题可表示为如下优化问题：

其中，损失函数前的系数C被称为正则化常数，当模型训练时结果与真实数据差距较大，则需要通过惩罚机制使模型训练结果趋于起初设定的目标。C也为惩罚系数，是不敏感损失函数，表达式如下：

损失函数的理解亦可直观表示为图10。

在损失函数的基础上，引入松弛变量和，且将落在左右两侧的松弛程度设置不一样，支持向量回归问题可表示为：

然后，引入拉格朗日乘子，得到上式的拉格朗日函数：

令对偏导数为零，并结合，可得：

此问题下KKT条件如下：

由上式得，当且仅当为0，可不为0。已知约束条件与不能同时为0，所以，至少有一个为0。

将偏导数为零的条件之一，代入可得SVR解形式如下：

使的样本即为支持向量回归的支持向量，该样本必落在ε间隔带外即，由KKT条件可求出，则由下式可求b，一般都会取多个满足的样本，得到b的平均值。

另外，可以将上述解写成特征映射形式，即可将SVR的解析解如下式，为核函数。

五、可转债定价实证

（一） 数据获取处理

数据来源：本文实证所需的所有数据，转债价格序列及转债因子数据都来自Wind金融终端及Tushare Pro平台。

数据时间段选取：本文选取2015年1月1日至2020年12月31日间所有交易数据不为空的转债标的，一共383只转债，包括中途退市转债。价格序列是该时间段的日频交易数据，每个转债从其上市日期起至2020年12月31日。因子数据从价格序列的时间点获取，一共1531个截面数据，根据前文分析，总共提取四大类因子，31个基础因子。

数据条拼接及数据集划分：因子数据与当日的价格序列对齐。非日频的因子及非时间序列的因子遵循最近原则。日期未公布的数据采用日期最近的数据填充。在拼接的所有价格因子数据条中，每月随机选取一个交易日的数据作为模型的测试集，并在剩下的数据中每周随机选取一个交易日作为模型的训练集数据，训练集数据与测试集数据不存在相同的数据条。

数据预处理：国内转债市场频繁出现暴涨暴跌的现象，以及因子缺失的数据条的处理对实证结果都有很大影响。主要步骤如下：

1.转债价格数据进行处理：去除成交量为0的数据，成交量为0大多数是转债遭遇停牌，本文认为当天价格并未反映最新的信息，予以剔除。

2.国内可转债市场存在少数规模较小的债券，T+0的交易规则下容易被少数持有者操纵交易，存在日内涨跌幅巨大的标的，严重偏离可转债的理论价值。因此，剔除单日涨跌幅绝对值超过20%的数据条。

3.对转债因子数据进行处理：因子数据数量级不一致时，直接输入模型会造成模型结果失效。因此进行标准化处理，即减去均值再除以标准差，方便后续同一量纲分析。

4.拼接数据，处理好价格数据及因子数据后，每月随机选取一个交易日的数据作为模型的测试集，并在剩下的数据中每周随机选取一个交易日作为模型的训练集数据，最终得到训练集数据21000条，测试集数据5800条。

（二）Black-Scholes模型实证结果

Black-Scholes模型广泛用于可转债定价领域，郑振龙和林海[7]将可转债的赎回条款作为微分方程的上边界，下修条款作为下边界，使用蒙特卡洛模拟和显性有限差分方法进行求解，结果显示当时我国的可转债市场价格都存在低估，并将此归因于当前的市场无效。但Black-Scholes方法并非完全适用于国内市场，蒋殿春、张新[13]很早之前指出Black-Scholes公式定价可转债内含期权是不准确的，并另外提出二项分布模型对可转债进行定价，以正股股价为主要驱动因素，并兼顾各项附加条款对可转债价值的影响，提高了模型定价的精度。

Black-Scholes模型中分别计算可转债的纯债价值和转股期权价值。纯债价值为可转债的各期现金流贴现值，贴现率使用对应期限对应评级中债企业债到期收益率;转股权价值等于内含转股期权的价值，等于转换为股票的份数乘以单个期权的价值，单个期权是以正股为标的资产，转股价为执行价格的看涨期权。具体计算步骤如下：

其中，为可转债现金流，取当日日期未来的现金流，即现金流发生日大于当日日期;为纯债贴现率，应用对应企业债收益率，这里选用中债指数收益率;为（现金流发生日-当日日期）/365;

为正股股价，为转股价格，为可转债剩余期限，σ为波动率，即正股过去一年的历史波动率，无风险利率为，这里采用一年期国债收益率。

Black-Scholes公式是目前运行稳定性最高的方法，理论意义强，能清晰刻画出转债价值的框架，且可以用来计算转债的瞬时敏感系数，但Black-Scholes公式存在将债券與期权相割裂的缺陷，也无法刻画回售赎回等诸多复杂条款。

此部分基于Black-Scholes模型的步骤，应用python进行实现，定义计算期权价值函数C（S，X，R，T，σ ）和债底价值函数C（Ci，R，T），对经过数据处理后的5800条测试集数据的价格进行测算，并通过计算以下指标观察Black-Scholes定价的效果：

1.平均绝对误差MAD，模型理论价格与市场价格的误差的绝对值的平均数;

2.平均绝对误差偏离度，绝对误差占市场价格的比例的平均值;

3.误差的标准差，观察两序列之间的误差是否稳定，衡量模型是否稳定;

4.误差大于0的比例，衡量Black-Scholes方法是否存在一直高估或者一直低估的状态。

Black-Scholes模型定价结果如表3所示，定价结果与市场价格误差的绝对值平均值为10.26，平均百分比误差为8.14%，精确度有所欠缺，但模型价格走势方向与市场价格基本一致。进一步来看，百分比误差的标准差较小，模型误差较稳定，不存在一直明显高估或者低估的情况。Black-Scholes模型可转债定价的精度有待提高，稳定性表现尚可。

（三）支持向量回归可转债定价

SVR可转债定价部分：输入变量为t日的31个因子数据，输出变量为t日的可转债理论价格，计算与t日的实际市场价格误差及误差的表现，并与前文Black-Scholes定价结果进行对比，观察定价的准确度及稳定性。

SVR价格预测部分：输入变量为t日因子的前五日滚动均值，输出变量为t日的预测价格，计算模型在测试集上的误差。

在构建实证模型前，对核函数的选择及核函数参数的选择及遍历空间有以下说明：

第一，支持向量回归核函数选择。学者魏瑾瑞[14]指出，支持向量机中的核函数是为了简化计算，不同的核函数具有比例很高的共同支持向量、存在相似性。因此在某种程度上，核函数参数的选择比核函数的选择更加重要，选定核参数最少的高斯核仅涉及gamma参数及模型自身的惩罚系数C。本文实证数据解释变量、训练数据测试数据条都较多，选取适用性最广的非线性核函数——高斯核函数，也称rbf核。高斯核相比于线性核，可以选择参数进一步优化，对于大样本和小样本均有比较好的性能，且对数据中存在的噪声具有较好的抗干扰能力。另外，高斯核相比于多项式核的参数较少。

第二，核函数参数设置。得出最优参数组的两种常见方法为穷举法和固定乘积法，其中为给定的常数。穷举法需要消耗更多时间及计算机算力，后者则能确定一个最优参数区，较为高效。本文结合及固定参数倍数的方法，确定不同的实证参数组合。参数γ意味着原始数据映射到高维数据后的分布，γ值的大小决定了分隔边界的弯曲程度。γ值过小，模型拟合度可能较低;γ值过大，对极端值也形成拟合，存在过度拟合。惩罚系数C一般为模型的敏感参数，衡量的是模型对损失样本的容忍度。

第三，输入数据。选取2015年1月1日至2020年12月31日间有交易数据的转债标的，一共383只转债，其中包括中途退市转债。价格序列是该时间段的日频交易数据。因子数据从价格序列的时间点获取，一共1531个截面数据。根据前文分析，总共提取31个因子。数据处理后最终得到训练集数据21000条，测试集数据5800条。

第四，参数敏感性分析。选用高斯核（RBF核）作为支持向量回归的核函数，有两个敏感性参数：C和γ。C为惩罚系数，默认设置为1，如果样本噪音较多，可将惩罚系数的初始值设置较小。γ为核函数参数，决定了样本映射后的分布。

第五，确定对参数的遍历空间。惩罚系数取C∈{0.05，0.1，0.5，1，5，10}，核函数参数取γ∈{0.0005，0.001，0.005，0.01，0.05，0.1}，两种参数组合一共有36种组合，在观察不同参数组合的绝对误差百分比、标准差及均值的表现情况，反映模型准确率的同时，也可以反映模型对参数的敏感性情况。这里将分别记录不同参数组合下，训练集及测试集上模型的表现，观察模型的稳定性。

依照上述步骤将训练集输入模型进行训练，得到模型后再输入测试集的31个转债因子，计算输出价格与测试集真实市场价格的差距，计算各项评价指标。支持向量回归SVR可转债定价结果如表4至表6所示：

从SVR模型的效果来看，综合表4、表5、表6三个指标的表现，表现最好的参数组合为C=10， γ=0.001。该参数组合下测试集的绝对误差百分比为1.98%，标准差为2.01%，绝对误差均值为2.49，意味着在经过21000条训练集数据训练后，在5800条测试集上的测算精度达到98.2%。预测精度较高，误差表现稳定，说明模型在经过充分训练后预测结果较为精确，可信度较大，定价结果较为精确。

另外，从参数敏感性来看，惩罚系数C相对核函数参数γ更加敏感，惩罚系数C默认参数为1。当惩罚系数C小于1时，惩罚系數越小，无论是在训练集还是测试集上，模型误差变大且波动也大，模型的精度及稳定性表现都不理想，这说明模型存在欠拟合;当惩罚系数大于1时，模型的总精度表现总体较优，但此时若γ值稍大，则模型在训练集上表现较好、测试集上表现不好，说明模型的核函数参数在0.01以上时，高斯核的特征边界弯曲度较大，模型存在明显的过拟合。核函数参数在0.01以下，γ敏感性明显降低，此时不会随着参数的改变模型的结果发生较大变化。

表7总结对比SVR和Black-Scholes定价实证分析，虽然支持向量回归模型对数据的深度广度要求更高、求解过程更耗时，但综合考虑模型的精确度及稳定性，支持向量回归模型给可转债定价的效果更加准确，模型稳定性更好。随着未来国内可转债市场逐渐规范化，机器学习模型有望在可转债定价理论实际投资领域得到进一步发展。

从图11、12中可看出，SVR方法得到的百分比误差更小、表现更稳定。综合表格中评价指标的表现及误差的波动情况，SVR误差99.10%都集中在10%以内，模型更精确。支持向量回归能大概率将定价误差控制在10%以内，相比Black-Scholes模型能提取出对价格具有解释力度的因素。

六、结论与建议

本文尝试应用支持向量回归定价国内可转债。从可转债价值的四大驱动力出发总结了31个因子，并同时给予逻辑解释和分层回测检验，分析其影响作用。为了形成对照，本文先基于Black-Scholes公式对可转债的转换期权和债底价值定价得到可转债价值，并进一步运用支持向量机回归方法拟合可转债价格，观察与Black-Scholes定价效果之间的差异。

本文应用支持向量回归做了两步实证：第一步是在所有的训练集和测试集上实证，确定惩罚系数为10，核函数参数0.001，输入变量为31个因子，输出结果为可转债的理论价格。结果显示SVR模型误差的各项指标均大幅优于Black-Scholes定价方法。第二步是基于大量的训练集数据，选取的10只可转债的历史时间序列价格进行预测，发现支持向量回归SVR依然能很好预测单个转债的下一日价格，模型预测价格能为可转债的市场价格提供参考。

综上，以上述31个因子作为输入数据，通过支持向量回归方法能很好地拟合出可转债价格，得到一个较为满意的可转债二级市场定价模型。在实际投资过程中，可以先结合因子选出具有投资价值的可转债标的，并支持向量回归的理论价格给出买入时点建议，形成自上而下先择券再择时的投资策略。

参考文献：

[1]ROMAN，L，WEIL，et al. Premiums on Convertible Bonds[J].The Journal of Finance，2012，23（3）：445-463.

[2]SCHWARTZ M.CONVERTIBLE BONDS：VALUATION AND OPTIMAL STRATEGIES FOR CALL AND CONVERSION[J].Journal of Finance，1977，32（5）：1699-1715.

[3]THOMAS S Y，HO，DAVID M，et al. Convertible Bonds：Model，Value Attribution，and Analytics[J]. Financial Analysts Journal，1996，（52）：35-44.

[4]GOLDMAN SACHS. Valuing Convertible Bonds as Derivatives[J].Quantitative Strategies Research Notes，1994，（11）：1-30.

[5]LONGSTAFF，FRANCIS A. Valuing American options by simulation：a simple least-squares approach[J].Review of Financial Studies，2001，14（1）：113-147

[6]DUBROV B. Monte Carlo Simulation with Machine Learning for Pricing American Options and Convertible Bonds[J].Available at SSRN，2015.

[7]鄭振龙，林海.中国可转换债券定价研究[J].厦门大学学报（哲学社会科学版），2004（2）：93-99.

[8]江良，林鸿熙，林建伟，等.基于随机利率模型可转换债券定价分析[J].系统工程学报，2019，34（1）：57-68.

[9]王茵田，文志瑛.向下修正条款对中国可转债定价的影响[J].清华大学学报（自然科学版），2018，58（1）：108-112.

[10]马林，黄中翔，刘天昀，等.可转换债券定价和实证研究[J].金融经济，2020（8）：82-86.

[11]程志富，胡昌生.杠杆交易限制下可转债的交换期权定价模型[J].管理工程学报，2020，34（1）：195-199.

[12]沈传河，刘中文，李缨.基于改进SVM的可转换债券价值分析与套期保值[J].系统管理学报，2016，25（1）：22-27.

[13]蒋殿春，张新.可转换公司债定价问题研究[J].国际金融研究，2002（4）：16-22.

[14]魏瑾瑞.对支持向量机混合核函数方法的再评估[J].统计研究，2015，32（2）：90-96.

Research and Empirical Analysis of Convertible Bond Pricing Based on Machine Learning

Niu Xiaojian，Ba Xiong

（Fudan University，Shanghai 200433，China）

Abstract：As a financial product featuring both bonds and stocks，convertible bonds have become an important financing tool in the capital market and an asset allocation tool favored by the majority of investors. However，due to the complexity of the additional terms and options of domestic convertible bonds，the strict assumptions of Black-Scholes formula often lead to a large deviation in the pricing results. The empirical results show that the 31 convertible bond factors summarized in this paper are taken as explanatory variables and the price of convertible bond can be well fitted through support vector regression.

Key words：convertible bond pricing;Black-Scholes model;machine learning;support vector regression