基于边值关系的面电流定义的重构

曹宏远，宋玲玲

（合肥工业大学 微电子学院，安徽 合肥230009）

0 引言

在场论中，电流I是一个通量，描述的是单位时间内通过某导体截面的电荷量。为了描述导电媒质中不同点的电荷运动情况，还需要引入电流密度的概念［1］。电流依据分布形态可分为体电流、面电流和线电流，相应地有（体）电流密度、面电流密度［1］。其中，体电流密度出现在麦克斯韦方程组第一式（），是磁场的涡旋源；而面电流密度出现在磁场强度的边值关系上（），它是导致场强切向分量在分界面上发生突变的场源。

然而，教材中在介绍面电流时，只是由体电流进行类比，然后直接给出面电流密度的公式，并没有讲述引入面电流的原因以及面电流与体电流之间的联系［1～3］。上述做法导致学生们认为：面电流就是存在于二维几何面上的电流，完全不同于体电流，是一个独立的物理量；当涉及到不同媒质分界面处存在切向电流密度突变时，媒质分界面上面电流密度等于切向电流密度之差。此外，教材中还曾提到，只有理想导体表面存在面电流，那么工程中应用的面电流又是什么呢［4～6］？

关于这些不准确的认识和困惑，本质上是初学者对面电流的定义没有形成清晰的物理图像。本文将从场强?边值关系的推演及面电流应用两个方面，构建面电流的物理图像，指出它与体电流的关联，为初学者及相关的工程技术人员的正确应用提供理论依据。

1 磁场强度边值关系的推演

图1所示是媒质1和媒质2的分界面。 为分界面法向单位矢量，由介质1指向介质2。场强由1区穿过分界面进入2区，在分界面周围取一个矩形闭合回路，两个长边分别在两种介质内并且与界面平行，长度为Δl（是一个小量，在这个小量上，场强视为常量），两个短边与界面垂直，长度为Δh（是一个高阶无穷小量）。

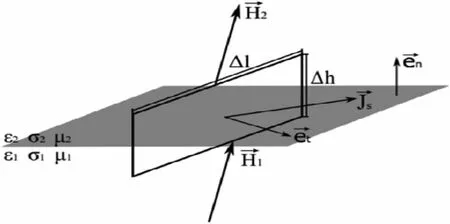
图1 磁场切向分量边界条件

图上，与分界面平行的方向都可以称之为切向，在有面电流存在的情况下，矩形回路所在平面并不一定与垂直，为推导方便，取矩形回路的法向单位矢量为，此处要求垂直，但不要求平行，可写成［7］。把积分形式的麦克斯韦方程组第一式应用于此闭合路径，有：

物理上，Δh→0描述的是一个无限靠近二维分界面的邻域，它是一个空间域，如图2（a）所示，对应到微观结构，这个空间域指的是1区、2区靠近分界面的几个分子层厚度的薄层，是媒质分界面的真实形态。若ΔI≠0，电流是分布在这个薄层里，从微观看，仍然是体电流，不是分布在二维几何面（Δh=0）上的电流。由于实验上所能测量的是宏观小微观大的一个区域内的物理量的平均值，可以将薄层内电荷的运动等效为集中在二维分界面（Δh=0）上的电流，如图2（b）所示。

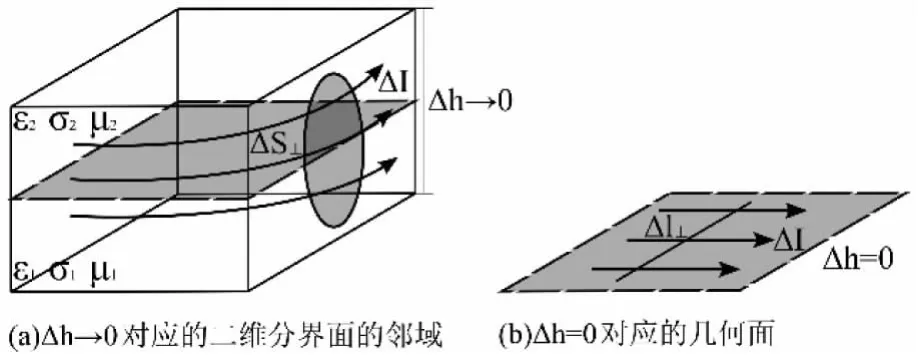
图2 分界面处面电流的形态

为了更细致的描述它在分界面上运动的特点，引入面电流密度定义：

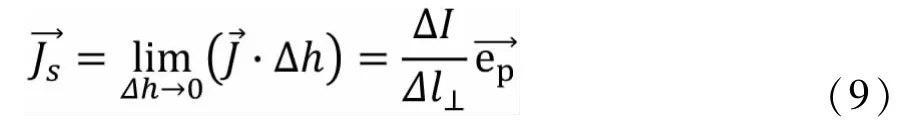
依据上述分析可知面电流是一种特殊形式的体电流，二者并不完全独立，因此，在分界面处不存在电流突变，这是与工程上的认识是一致的。那么，在分界面处是否存在电流密度突变？电流密度突变会是否导致面电流密度的产生？通过对在两种导电媒质分界面上电场强度的边值关系再推演，进一步阐述这些问题。

2 两种导电媒质的分界面

推导电场切向边值关系时用到了麦克斯韦方程组第二式的积分形式：

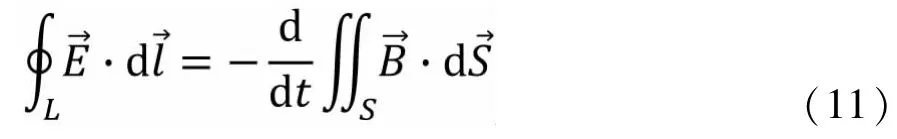
（11）式可视为麦克斯韦方程组第一式的特例，即相当于第一式中=0的情况，于是可得：

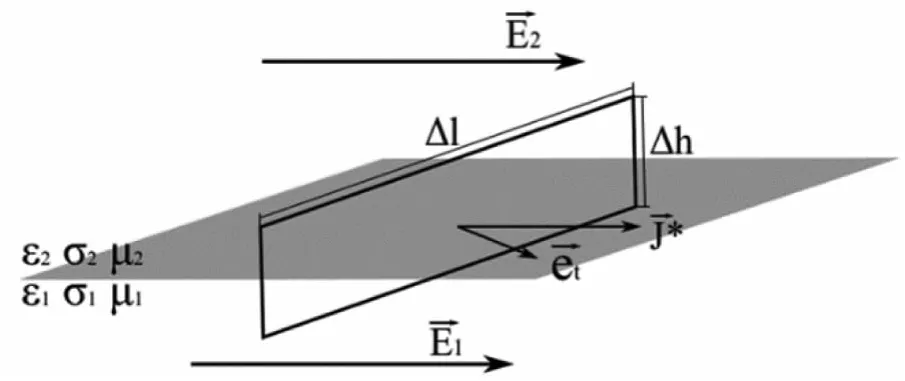
图3 电导率有限的导电媒质分界面

积分结果可以表示为I，代表从分界面的邻域流出的电流。当Δh→0时，被积函数为有限值，I=0，因此没有电流从分界面上流出，即不存在面电流。通过上述证明可知切向电流密度突变并不一定会导致面电流密度产生，两者之间没有因果关系。

事实上，切向电流密度的突变以及面电流的产生都是由于在物理上常常将分布在媒质表面邻域内的薄层等效为二维平面所导致的，两者的区别在于切向电流密度的突变在两种导电媒质的分界面必然存在，而面电流必须在理想导体表面才会存在。

3 面电流的应用

电导率σ→∞的理想导体表面，切向电流密度之差趋于无穷大，由（13）式可知理想导体表面存在面电流。虽然理想导体实际上是不存在的，但它却是一个非常有用的概念，例如电磁波入射到金属表面时，几乎是全反射，如果忽略折射到金属内部的电磁波功率，则金属表面可以用理想导体表面代替，简化边值问题的分析［9］。此时，依据场强的边值关系，电磁波在金属表面就会感应出面电流密度。这种简化过程，也符合物理实际-趋肤效应。当导体中有交流电或者交变电磁场时，导体内部的电流分布不均匀，若频率足够高，且电导率足够大，电流就会集中在导体外表的薄层，导线内部实际上电流几乎为0，在宏观上，可以将其看成面电流分布［1］。

在工程上，面电流是一个广泛使用的物理量，例如，一个密绕的螺线管中的电流可以看成面电流；通过面电流传感器测试和研究金属壳体的电流；构建精确的面电流分布模型实现螺旋线行波管的优化设计等等［5～6］。

面电流分布的另一个例子是磁性物质表面的磁化电流［2］。当介质被磁化后，内部分子磁矩都有一定的取向，在磁介质内部，分子电流相互抵消；靠近磁介质表面，分子电流则构成宏观的磁化电流面分布。磁化面电流实际上是靠近表面相当多分子电流的平均宏观效应。

4 结语

本文针对现有的一些电磁场教材在讲述面电流时有所含混不清的情况，从相关场强的边值关系的推导出发，详细梳理了面电流的由来，构建了面电流清晰的物理图像，并澄清了不同媒质分界处存在切向电流密度突变时，分界面上面电流密度的情况，有助于读者对相关知识的深入理解与应用。

物理上常常将媒质表面邻域的薄层等效为二维平面，将分布在薄层内的体电流等效为二维面电流，面电流密度则强调电荷在面空间上的运动和分布。在不同媒质的分界面上虽然存在切向电流密度突变，但并不一定存在面电流，只有当切向电流密度之差趋于无穷大，即理想导体表面上存在面电流。因此在学习过程中绝不能把切向电流密度之差当作面电流密度的值。虽然理想导体实际上并不存在，但它却是一个非常有用的概念。在工程上合理使用面电流这一物理量，将简化实际电磁现象问题的分析。