化难为易解决问题

□邱廷建

小朋友，你会数图形吗？你能不重复也不遗漏地数出线段、三角形、长方形的个数吗？我们可以运用化难为易的数学思想方法，寻找、发现图形中的规律，并根据发现的规律解决问题。

例1 如图1 所示，一条铁路上有12 个停站点，一共需要多少种不同的车票？

图1

［分析与解］ 可以把这道题转化为用数线段的方法来解答。如果直接数，容易数错，我们可以化难为易，先思考单程，依次从第一个站点出发、第二个站点出发、第三个站点出发……需要准备多少种车票，然后思考返程。

思考单程，从图2 中可以看出，从第一个站点出发，到达其余的11 个站点，需要11 种车票；从第二个站点出发，到达其余的10 个站点，需要10 种车票；从第三个站点出发，到达其余的9 个站点，需要9 种车票……按此规律进行类推，从第十一个站点出发，到达最后1 个站点，需要1 种车票。最后运用加法计算，单程行驶一共需要车票11＋10＋9＋8＋7＋6＋5＋4＋3＋2＋1＝66（种）。

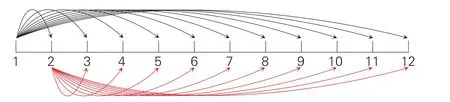
图2

再思考返程，也需要设计同样数量的车票，所以一共需要车票66＋66＝132（种）。

例2 数一数，下面的图形中有多少个三角形？

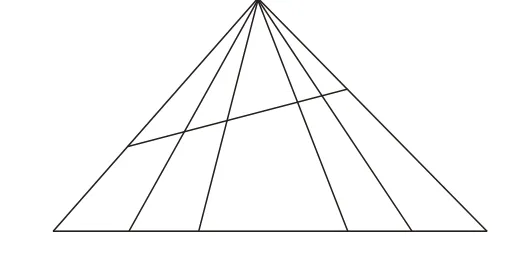
图3

［分析与解］这个图形比较复杂，要数出它有多少个三角形，比较繁难，也容易数错。因此我们可以化难为易，把这个复杂的图形转化为比较简单的图形（如图4、图5）。

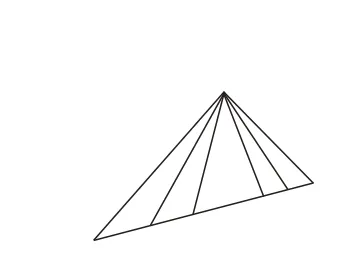
图4

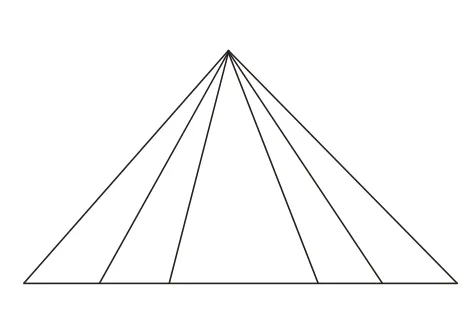
图5

从图4 中可以看出，以最左边的一条边为边的三角形共有5 个（如图6），从左边起第2 条边为边的三角形共有4 个，从左边起第3 条边为边的三角形共有3 个，从左边起第4 条边为边的三角形共有2 个，从左边起第5 条边为边的三角形有1 个。因此图4 中的三角形一共有5＋4＋3＋2＋1＝15（个）。

图6

用同样的方法，可以数出图5 中的三角形一共有15 个。因此原来图形中的三角形一共有15＋15＝30（个）。

从上面的数三角形中，我们可以发现规律：要数出图中三角形的个数，只要数出三角形底边一共包含了几条线段就可以了。图4 的底边一共包含有线段5＋4＋3＋2＋1＝15（条），所以图4 中一共有15 个三角形。同样，图5的底边一共包含有线段15 条，所以图5 中一共有15 个三角形。

例3 数一数，下面的图形中有多少个长方形？

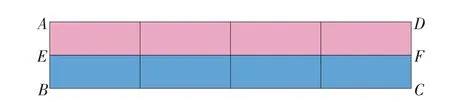
图7

［分析与解］可以化难为易，把这个复杂的图形转化为三个比较简单的图形（如图8、图9、图10），再把每个图形转化为用数线段的方法来解答。

图8

图9

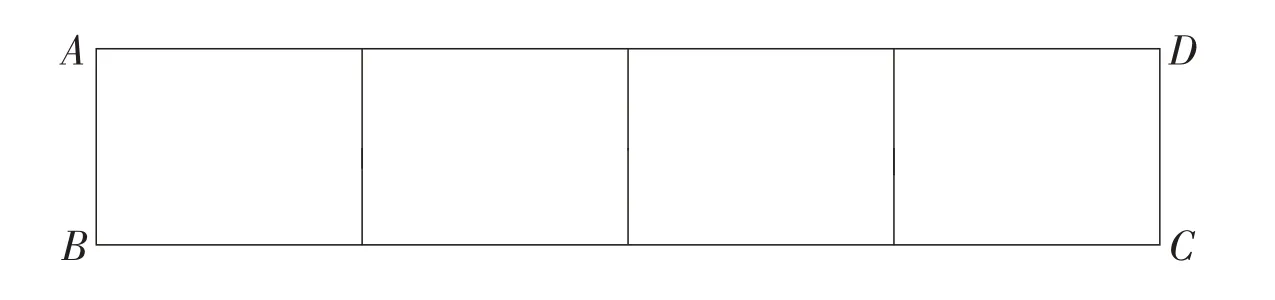
图10

从图8 中可以看出，AD这条线段，以最左端A点为端点的线段共有4条，从左端起第2 个点为端点的线段共有3 条，从左端起第3 个点为端点的线段共有2 条，从左端起第4 个点为端点的线段共有1 条。因此图8 中的长方形一共有4＋3＋2＋1＝10（个）。

用同样的方法，可以求出图9 中的长方形一共有4＋3＋2＋1＝10（个），图10 中的长方形一共有4＋3＋2＋1＝10（个），因此原来图形中的长方形一共有10＋10＋10＝30（个）。

也可以这样解答，数出AD这条边上有10 条线段，AB这条边上有3 条线段，因此原来图形中的长方形一共有10×3＝30（个）。