关于热力学定律的一些讨论

李 炜，周 正，娄 捷，修发贤

(复旦大学 物理学系，上海 200433)

在物理学的众多研究方向中热力学是与我们生活最密切相关的一门基础学科之一[1],它是一套从宏观层面上系统性地研究物质的热运动性质及其规律的物理理论,其理论基础主要体现在热力学的四大基本定律上,特别是热力学第一定律揭示物质和能量之间的转化与守恒关系,以及热力学第二定律揭示宏观物质演化的不可逆过程进行的方向性,即与具有时间反演对称性的经典力学和量子力学理论截然不同的是,宏观物质世界实际上是一种具有时间反演对称性破缺的系统[2-3],由此而呈现出生物的生命有限和宇宙膨胀等客观物理规律.

对于时间反演对称性破缺的热力学系统,它实际上与在理想气体温标下具有绝对零度不能达到的特征的热力学第三定律存在着千丝万缕的联系.因此,在本文中我们将主要讨论时间反演对称性破缺的热力学第二定律和绝对零度不能达到的热力学第三定律之间的关系,尤其是我们将通过Carnot热机循环效率从定量层面上阐述它们之间的关系,即绝对零度如果一旦能够达到,那么也就意味着Carnot热机循环效率能够达到100%的效率.同时,我们还从微观角度上给予统计解释.另外,我们还将继续系统性地讨论热力学函数,如体系的内能、焓、Helmholtz自由能和Gibbs自由能等，在实际的热力学系统中的应用,特别是在当前有关铁电和铁磁研究领域中的讨论与应用.

1 热力学定律

1.1 热力学参量

1.2 热力学定律

根据大量的宏观热力学实验,科学家们揭示出宏观物质具有4条基本的热力学定律[1,5]：

(1) 热力学第零定律,即处于平衡态中的热力学系统温度处处相等.该定律揭示出温度在热力学平衡态系统中的普适性地位.

(2) 热力学第一定律表述为热力学系统的热量可以从一个物体传递到另一个物体,也可以与其他能量或者物质发生相互转换,但是在其转换过程中,能量的总值保持不变,即不同形式的能量或者物质在传递与转换过程中依然保持着不变.该定律也被称为能量守恒定律.用数学语言表述为系统的内能变化ΔU等于外界对系统所做的功W与系统从外界所吸收的热量Q的总和.

(3) 热力学第二定律指出宏观热力学系统在演化过程中所经历的是不可逆的过程,即宏观热力学系统的不可逆过程进行的方向性,它是破坏时间反演对称性的.因此,我们可以构造理想化的可逆循环过程来估算实际的宏观热力学系统所经历的不可逆过程的效率.例如在理想气体的Carnot可逆循环过程中,它包含着两个等温过程和两个绝热过程,详细如图1(a)所示,系统从高温热源T1处通过对外做功吸收Q1热量,然后在低温热源T2处通过外界对系统做功放出Q2热量,其热机循环效率为

图1 (a) 热机循环过程示意图; (b) 卡诺热机工作示意图Fig.1 Schematic diagram of (a) Carnot cycle and (b) Carnot engine

(1)

如图1(b)所示.对于不可逆的理想气体，Carnot循环过程因为系统在循环演化过程中会额外地散失一部分热量,于是不可逆的热机循环效率η′总是会小于理想化的可逆循环效率η.

(4) 热力学第三定律指出在理想气体温标下绝对零度是不能达到.从分子动力学角度分析,温度代表着微观粒子热运动的平均动能,绝对零度不能达到也就意味着系统中的微观粒子始终处于热运动之中.

2 热力学定律的讨论

热力学的4条基本定律构筑着整个热力学系统的宏观理论体系,也代表着宏观物质客观运动的物理规律,典型代表的是具有能量守恒规律的热力学第一定律和具有时间反演对称性破缺的宏观热力学系统随时间演化不可逆过程的方向性的热力学第二定律.然而对于在理想气体温标下绝对零度不能达到的热力学第三定律来说,它实际上与热力学第二定律有着千丝万缕的隐含联系.下面我们将主要讨论具有时间反演对称性破缺的热力学第二定律和具有绝对零度不能达到的热力学第三定律的关系及其微观统计理论解释[1,5]：

(1) 根据热力学第二定律可知,任何一个实际的不可逆循环过程的热机效率始终小于1,即实际热机效率η′<1;

(2) 如果我们假设热力学第三定律不能成立,即可以存在一个宏观热力学系统,它的绝对温度不仅可以达到绝对零度,而且还可以降低至负温度,那么根据理想气体的Carnot可逆循环过程,如图1所示,我们让低温热源的温度T2逐渐地趋近于绝对零度,甚至到达负温度,其热机效率为

(2)

与热力学第二定律相违背,所以绝对零度不能达到.因此,热力学第三定律与热力学第二定律之间存在着密切的关系.另外,从分子动力学角度分析,温度代表着微观粒子的平均动能,在理想气体温标下它是一个非负值,所以负温度是不允许存在于客观物理的热力学系统之中的.同时,绝对零度意味着微观粒子完全地处于有序冻结状态[5,8],Boltzmann熵为零,它与孤立系统的熵总是朝着熵增加方向演化和系统趋于无序方向演化相矛盾.这也暗示着在理想气体温标下热力学系统的绝对零度不能达到的客观物理规律.

3 热力学函数

根据热力学第一定律,当系统的体积保持不变时,我们很容易地用系统的内能的微分形式描述宏观热力学物质系统的状态：

dU=dQV=CVdT，

(3)

其中：CV=dQV/dT为系统的等体热容,表示热力学系统在等体积变化时升高单位温度所吸收的热量,它是一个实验可观测的物理量.当系统的压强保持不变时,外界对系统做的微功dW=-PdV,这时我们需要通过Legrendre变换引入新的状态函数[5],焓H=U+PV,其微分表示为

dH=dU+PdV=dQP=CPdT.

(4)

其中：CP=dQP/dT为系统的等压热容,表示热力学系统在等压强变化时升高单位温度所吸收的热量,它也是一个实验可观测的物理量.尽管从式(3)和(4)中可以看出,等体积和等压强演化过程中热力学系统状态函数的微分可以通过热容表示,但是对于等温度演化过程中的热力学系统却不能再用热容来表示.这时我们需要进一步推广热量的定义.幸运的是热力学第二定律引入一个新的状态函数[5],熵S.因此,热力学系统的状态函数内能U和焓H的全微分可以重新改写为

dU=TdS-PdV，

(5)

dH=TdS+VdP.

(6)

由式(5)和(6)可知,内能U是以熵S和体积V为参量的状态函数U(S,V),而焓H是以熵S与压强P为参量的状态函数H(S,P).但是我们已经在上述热力学参量部分讨论过熵S不是热力学系统的变化参量,于是我们需要再次通过Legrendre变换引入新的两个状态函数[5],Helmholtz自由能F=U-TS和Gibbs自由能G=F+PV,于是

dF=-SdT-PdV，

(7)

dG=-SdT+VdP.

(8)

从以上两式可以看出,Helmholtz自由能F是以温度T与体积V为参量的状态函数F(T,V),而Gibbs自由能G是以温度T与压强P为参量的状态函数G(T,P).在实际的热力学系统应用中，当系统的体积V与温度T容易调控时,我们采用Helmholtz自由能F(T,V)作为热力学系统的状态函数；如果热力学系统的压强P与温度T较为容易调控时,我们则采用Gibbs自由能G(T,P)作为热力学系统的状态函数.然后从这些热力学的状态函数出发,继续导出所有其他的热力学状态函数,例如以温度T与压强P为变化参量，从Gibbs自由能的微分表达式(8)出发,我们可以得到

(9)

(10)

分别表示为热力学系统的熵和系统的物态方程,并代入Gibbs自由能的定义中我们得到内能的表示形式[5]：

(11)

同样的道理,我们以温度T和体积V为热力学变化参量，从Helmholtz自由能F(T,V)中推导出热力学系统的内能表示形式：

(12)

一旦确定热力学系统的变化参量和状态函数,我们就可以系统地研究该热力学物质系统的状态函数随变化参量的演化物理规律[1,5].

4 热力学状态函数在铁磁和铁电系统中的应用

在上部分中我们主要讨论一般性的热力学系统的状态函数的性质.对于凝聚态物质系统,它们的体积往往是不易被改变的,而实验往往是在一个大气压环境下进行.因此,我们需要将压强对体积所做的功推广到表征我们所要研究对象物质性质的广义功,如外加磁场对铁磁系统所做的功和外加电场对铁电系统所做的功.对铁电和铁磁系统方面的研究是当前前沿凝聚态物理学最重要的研究领域之一,它们在信息技术行业中有着广泛的应用[9-12].下面我们将简要地讨论热力学状态函数在铁磁和铁电系统中的应用.

(13)

其中第1项表示为真空中磁场能量密度,第2项表示为外加磁场对磁性介质磁化过程中所做的功,它是我们主要感兴趣的研究对象的物理性质.因此,我们可以写出磁性材料在磁化过程中的内能状态函数为

(14)

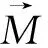
(15)

(16)

其中第1项表示为真空中电场能量密度,第2项表示为外加电场对电介质极化过程中所做的功,它是我们主要感兴趣的研究对象的物理性质.因此,我们可以写出电介质材料在电极化过程中的内能状态函数为

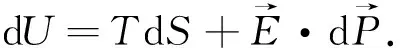
(17)

(18)

5 结 语

在本文中我们首先通过Carnot热机循环效率揭示出宏观热力学第二定律和热力学第三定律之间的联系,即在理想气体温标下绝对零度如果一旦能达到,那么也就意味着Carnot热机循环效率能实现100%的效率.同时,我们还从微观统计层面上给予统计解释.此外,对于热力学状态函数的性质及其在当前有关铁电和铁磁性系统中的应用方面给出简要讨论.这些内容的讨论都将会为今后的本科生基础物理的学习与教学以及在当前有关多铁性方面的科研提供重要的思路与参考资料.