一种基于空间光机热模型的自适应PID控制方法

李 帅，杨宝玉，陆 燕

一种基于空间光机热模型的自适应PID控制方法

李 帅1,2，杨宝玉1，陆 燕1

（1. 中国科学院上海技术物理研究所，上海 200083；2. 中国科学院大学，北京 100049）

为提高空间相机的控温稳定度以保证成像质量，本文提出一种基于空间光机热模型的自适应比例积分微分（proportional-integral-derivative, PID）控制方法。该控制器的设计从空间光机的热平衡方程出发，能够实时根据光机及与其辐射换热对象的温度修正光机的热模型，继而采用极点配置的方法实时校正PID控制器参数，最终确定本控温周期的加热占空比。本文通过建立抽象的空间光机热模型，分别施加上述自适应PID控制方法与固定参数PID控制方法，对控温效果进行了仿真及实验对比。结果表明，对环境扰动引起的温度波动，该自适应PID控制器始终保持最佳动态响应，控温稳定度优于±0.1K，具有更好的控温稳定性和环境适应性。

空间光机；热模型；极点配置；自适应；PID控制

0 引言

空间相机是实现对地观测、大气和海洋探测及宇宙探测等应用的主要有效载荷，根据不同的探测要求，相机精度和成像质量也有不同要求。对高精度相机其光机温度对成像质量的影响受到广泛关注，当温度发生变化时，一方面镜片表面的曲率半径、透镜的厚度、光学材料的折射率均会发生改变[1]，另一方面由于镜框的热膨胀系数较大，镜框会相对于镜片发生差分膨胀或收缩[2]，这均会造成焦距偏离和系统失准，导致相机成像模糊，严重时甚至出现成像失败的情况。

空间光学遥感相机在轨工作时，由于太阳辐射、地球红外辐射、地球反照、空间背景辐射的交替变化，造成相机的光机周围结构温度发生剧烈变化，周围结构通过辐射换热影响光机温度也发生波动。为使相机的光机维持在稳定的温度水平以保障成像质量，除采用被动热控措施外，一般光机还采用直接或间接的主动控温加热回路，通过控制加热器的加热功率，精确补偿损失的热量，实现光机温度的稳定控制。相机在具有宽视场及高分辨率的要求场合，光机对控温稳定度提出了更高的要求。例如“高分二号”卫星，其上两个相机的主镜、次镜、次镜支撑件、前镜筒等光机结构都要求在控温精度为20℃±2℃时，控温稳定度为±0.3℃/h[3]；空间太阳望远镜（space solar telescope，SST）的主镜镜面在等直径的环上控温稳定度为±0.1℃/h[4]；Herschel卫星的远红外光学系统要求10s内控温稳定度≤3×10－4K[5]。

为提高控温稳定度，除了需要对光机及其周围环境进行合理的热设计，设计多个主动控温回路以及采用多级控温策略[6-8]外，改进温度控制算法对提高控温稳定度的效果更为突出。目前，空间光学遥感相机上大多采用开关比例控制的控温方式，一些重要结构部件则采用控温稳定度更高的固定参数PID控制。固定参数PID控制具有控制算法简单、技术成熟、可靠性高，为大多数工程师所熟悉的优点，能够满足大多数被控对象的控温要求[9]。但其仅依据被控对象控温点的温度做控制决策，不论与被控对象存在热关联的周围热环境如何改变都采用不变的PID控制参数，这可能给被控对象的温度带来不必要的波动。虽然有些文献中指出控制的动态和稳态特性取决于所设置的PID参数[10-12]，并由此发展出模糊自适应PID控制、专家PID控制、基于模型辨识的自适应PID控制等智能控制方法。模糊自适应PID控制、专家PID控制等基于规则的PID参数自整定方法简单，在线控制容易实现，但整定出的PID参数并不是该控温系统在该时刻的最优参数；基于模型辨识的自适应PID控制的在线辨识较为复杂，计算机计算量大、工作时间长，而且还需要解决闭环可辨识性问题。因此，这些智能控温方法尚未在空间相机的工程实践得到应用。目前，国外在空间相机的温度控制中采取了基于被控对象热特性的自适应PID控温算法，提高了系统控温稳定度。例如，“普朗克”卫星光学系统的控温算法是最优PI（proportional-integral）控温算法，该算法从被控对象的解析模型出发，建立了一组可供探索的参数列表，以确定空间环境下仪器运行的最优传递函数，然后利用该温控系统的传递函数模型实现PI控制参数的最优整定[13]，实现控温稳定度优于±0.1K；“Herschel”卫星的远红外光学系统采用自适应PI控温算法，该算法通过热平衡试验获取的温度数据修正热分析模型，根据修正后的热分析模型，确定各个部件的传递函数，从满足其温度稳定性要求出发，重新整定PI控制器参数[5]，实现控温稳定度优于±0.5K。我国在空间相机的温度控制领域，暂未出现基于被控对象热特性的自适应PID控制方法应用案例，PID控制器参数未能结合具体控温对象进行设计，导致系统难以实现高稳定度的温度控制。

本文从空间光机抽象模型的热平衡方程出发，提出了一种能根据光机及与其辐射换热对象的温度实时修正光机数学模型，继而采用极点配置的方法实时校正控制器参数的自适应PID控制方法，利用建立的空间光机抽象模型对该控制方法的控温效果进行了仿真及实验验证。

1 控温原理

空间光机的主动加热控温回路一般包括温度控制器、测温用热敏电阻（或热电偶、测温二极管等）、加热器等。图1为本文提出的基于空间光机热模型的自适应PID控温原理图。该温度控制器需要同时采集被控对象及与其存在辐射换热的周围环境的温度，通过计算出等效辐射换热系数来修正被控对象模型，然后以二阶最佳动态响应模型为目标，利用极点配置设计PID参数，输出加热占空比，最终通过加热器实现被控对象的高稳定度温度控制。该自适应PID控制方法具体设计过程详细介绍如下。

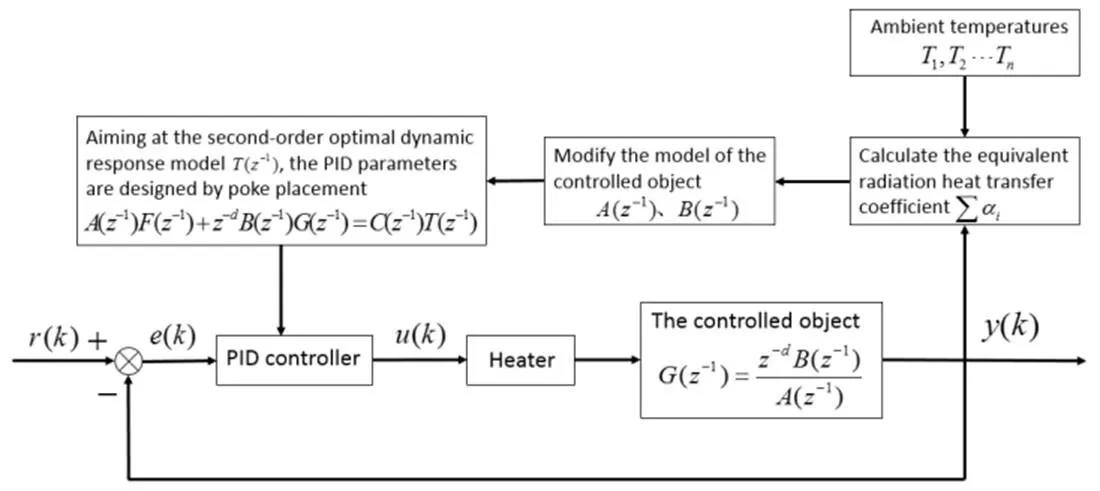
图1 基于空间光机热模型的自适应PID控温原理图

1.1 被控对象热模型

对于某空间光机的控温系统，设其控温点的温度为m，与该控温区域存在传热的周围环境的温度分别为1，2，…，T，空间相机处于真空环境，只存在热传导和热辐射两种传热方式，忽略单个测温区域的温度分布不均匀性，建立光机的热平衡方程：

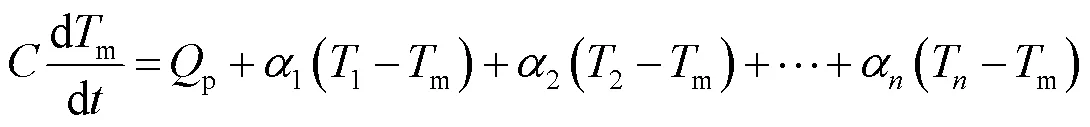
式中：p为加热器功率；为光机的总热容；（其中，1,2,···,）为光机与换热对象之间的等效换热系数。

对于导热换热，一般视为不随温度变化的常数，甚至由于光机的安装一般使用接触面积小、导热率低的钛合金螺钉和隔热垫安装，导热换热的等效换热系数i可以忽略不计，而对于辐射换热，可由(2)式进行计算：

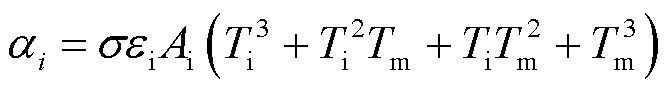
式中：为斯忒藩-玻尔兹曼常量，其值为5.67×10－8W/(m2·K)；i为光机与辐射换热对象i之间的系统发射率；i为光机与辐射换热对象i之间的辐射换热面积。

对式(1)两边做拉普拉斯变换，可得光学对象温度m与加热器功率p和其他换热对象温度i之间的关系如下：

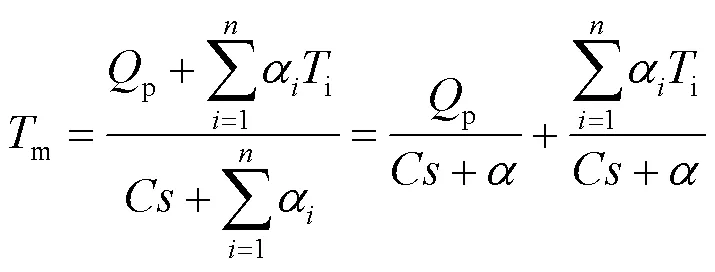
由于加热器功率p的变化反映到光机温度的变化存在一定的滞后时间，所以加热器功率p和光机温度m之间的传递函数p()为：

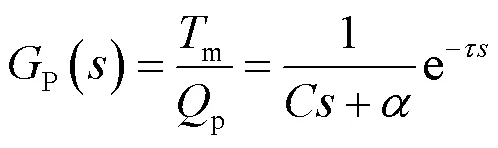
由式(4)可得p()带零阶保持器的广义对象脉冲传递函数为：

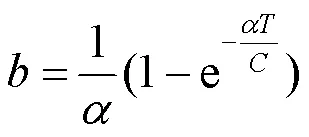
由式(2)可知，当光机及与其辐射换热对象的温度变化时，随之发生变化，加热器功率p和光机温度m之间的传递函数p(－1)即发生改变。即能够通过跟踪光机及与其辐射换热对象的温度对光机的热模型进行实时修正。

1.2 极点配置自适应PID控制算法

1）极点配置控制器算法

设被控对象受控自回归滑动平均（controlled auto regressive moving average, CARMA）模型为：

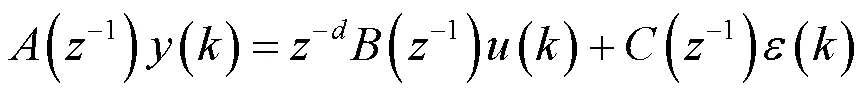
式中：()、()、()分别为被控对象的输出、输入和不可检测的零均值白噪声序列；－1为后移算子；为滞后步数；(－1)、(－1)、(－1)均为－1的多项式。

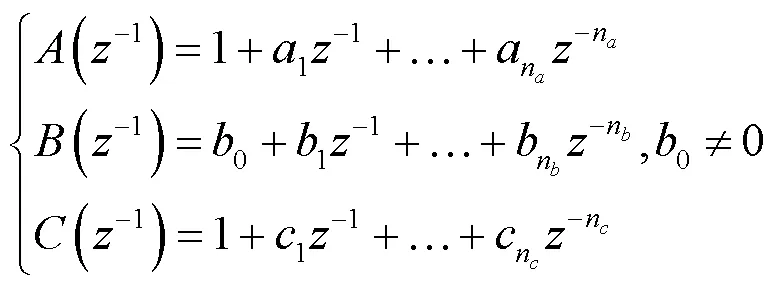
根据式(5)可得出：

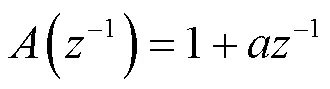
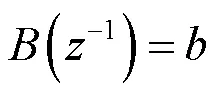
常规的计算机闭环控制系统的结构可表示为图2。

图2 计算机闭环控制系统结构图

由图2可得，该系统的闭环方程为：

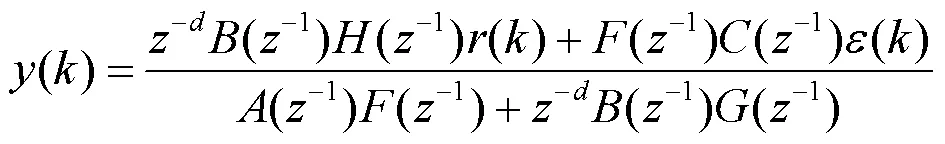
从式(10)中可知，根据增广型自校正闭环极点配置[14]的要求，闭环特征多项式为：

式中：(－1)为期望特征多项式。

进行极点配置时，一般以典型的二阶系统闭环传递函数的标准形式作为目标。

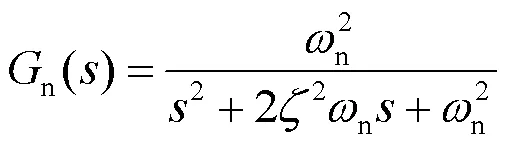
与式(12)相对应的离散特征多项式为：

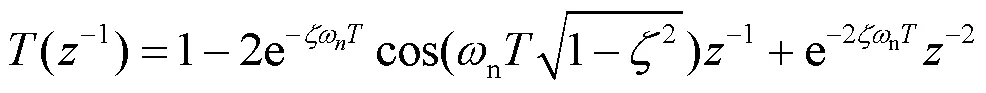
式中：为阻尼比；n为无阻尼自然振荡角频率。

对式(13)，当二阶系统最佳阻尼比＝0.707时，为二阶最佳动态模型，在单位阶跃作用下的超调量%＝4.3%，相角稳定裕量(c)＝65.5°。

采样周期和n、的关系可按下式计算：

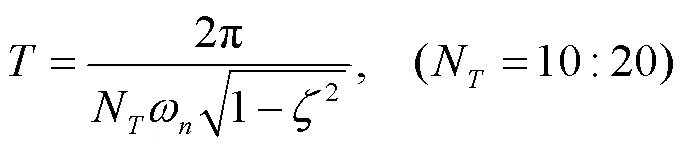
图2系统可直接写出极点配置自校正控制器输出()的表达式为：

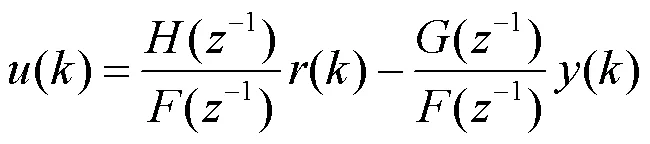
2）增量型PID控制算法

在数字系统中，通常采用带有数字滤波器的PID控制器算法[15]：

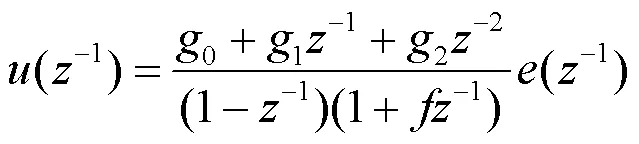
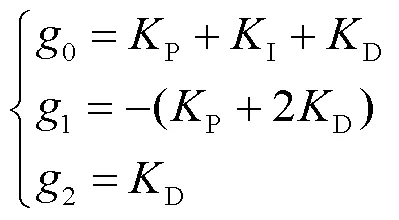
式中：P为比例系数；I为积分系数；D为微分系数。

方程组(14)对P、I、D有唯一解，即：

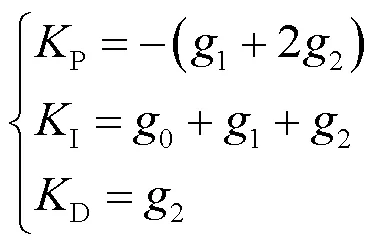
3）极点配置自适应PID控制算法

为将极点配置控制器变换为增量型PID控制器，对照式(16)，式(15)选用下述形式：

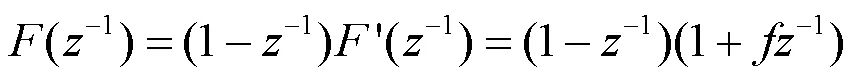
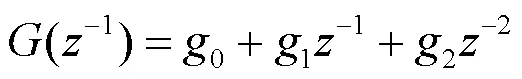
由式(15)可知，为保证系统稳态误差最终为零，还需选择：

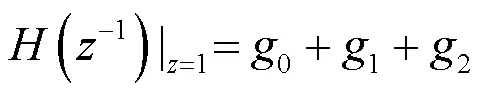
式(11)中选择多项式(－1)时应防止在系统输出端出现突变而导致振荡[16]，因此考虑选择：

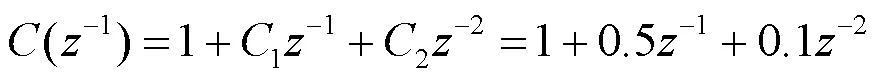
采用极点配置法整定PID控制器参数，即是选取PID参数，使系统具有期望的闭环特征方程。所以将式(8)、(9)、(13)、(19)、(20)、(22)代入式(11)，令方程式(11)两边系数相等，解代数方程即可求得0、1、2，最后根据式(18)即可求得以二阶最佳动态模型为目标的PID参数。

该控温方法与固定参数的PID控温方法相比，当光机及与其辐射换热对象的温度变化时，该控温方法能够对光机的热模型进行实时修正，然后采用极点配置的方法以二阶最佳动态响应模型为目标实时校正PID控制器参数，使PID控制器的动态控温性能始终保持最佳状态，因而有助于减小光机由于热惯性造成的不必要的温度波动，具有更好控温的稳定性。

2 仿真及实验验证

为了对该控温方法进行仿真及实验验证，本文建立光机的热控系统模型如图3所示。

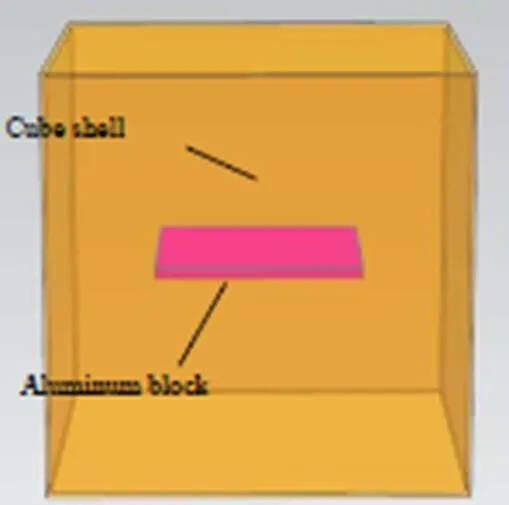
图3 光机热控系统模型

建立被控对象（铝块）的数学模型，取滞后时间＝2s，由上文中分析可得：

加热器功率p与铝块温度m之间的传递函数p()为：

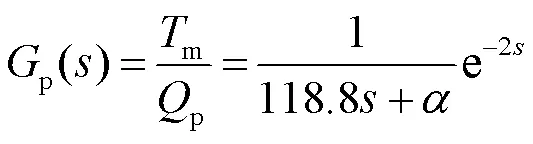
环境温度s与铝块温度m之间的传递函数s()为：

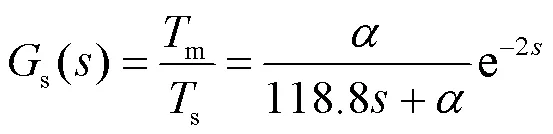
式中：

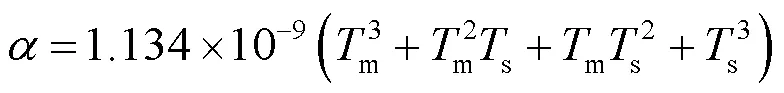
取采样时间＝＝2s，由上述1.1节的分析可得p()带零阶保持器的广义对象脉冲传递函数为：

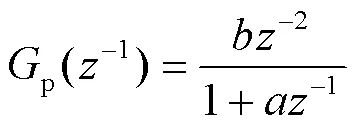
由上述1.2节中分析可得PID参数，

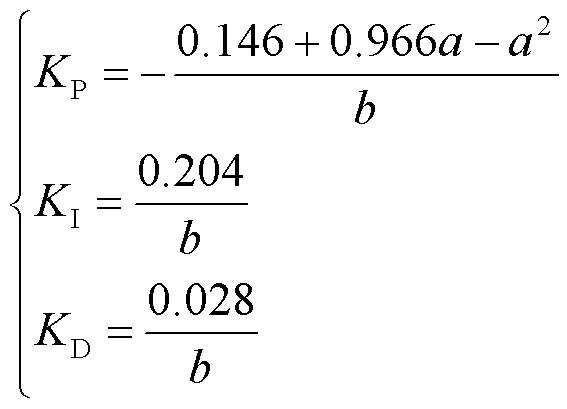
2.1 仿真验证

上述热控系统的仿真模型借助MATLAB软件编程建立，该自适应PID控温方法与固定参数PID控温方法的仿真结果如图4所示。对于不同的环境温度，PID控制器的最佳动态响应参数不同，图中两个固定参数PID控制器的PID参数为控温过程中某一温度下被控系统模型对应的最优PID参数，PID控制1的控制器参数为：P＝0.412，I＝0.050，D＝0.007，PID控制2的控制器参数为：P＝0.447，I＝0.045，D＝0.006。

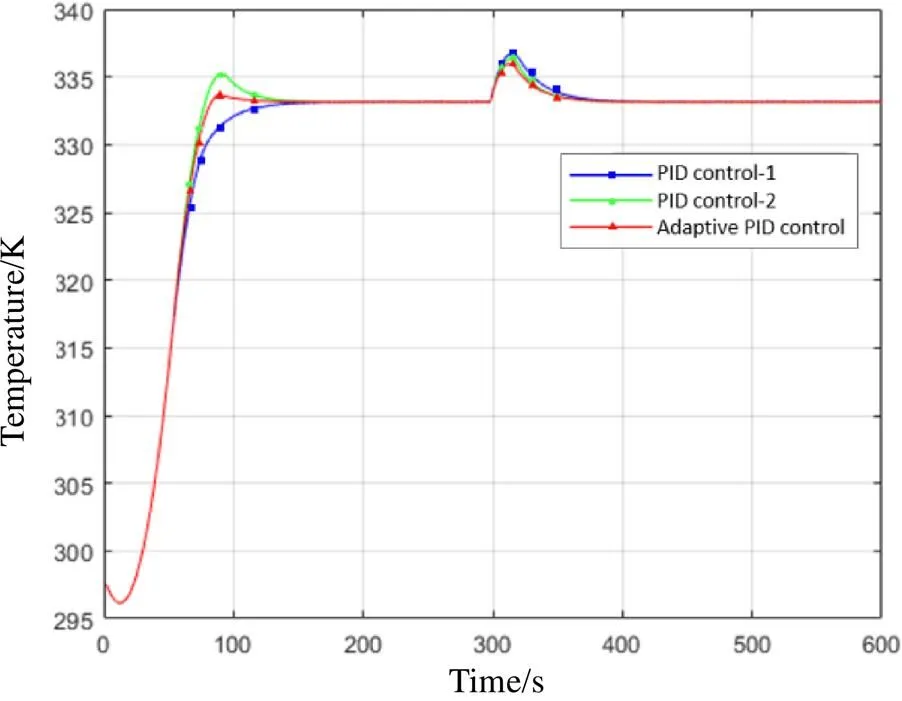
图4 仿真结果对比

图4中0时刻为环境温度保持298K时，控制器的阶跃响应，结果显示在铝板升温并稳定在(333.15±0.1)K过程中，PID控制1所需时间为135s，超调量为0；PID控制2所需时间为132s，超调量为2.15K；自适应PID控制所需时间为108s，超调量为0.55K。结果表明随着被控对象温度的改变，该PID控制器始终保持最佳动态响应，收敛更快。

图4中在300s时刻，使环境温度快速上升至323K，模拟空间环境外热流的大幅值增大，结果显示铝块温度再次恢复稳定到(333.15±0.1)K过程中，PID控制1超调量为3.55K；PID控制2超调量为3.15K；自适应PID控制超调量为2.85K。结果表明随着空间环境外热流大幅值增大导致环境温度快速升高，控温系统的数学模型发生改变时，该PID控制器始终保持最佳动态响应，超调量小，调节时间短，抗干扰性更强，控温稳定性更好。

2.2 实验验证

将上述光机热控系统模型放置于真空罐内进行实验，该自适应PID控温方法与固定参数PID控温方法的实验结果如图5所示，图中固定PID控制器参数的选取与上文中仿真的控制器参数选取一致。

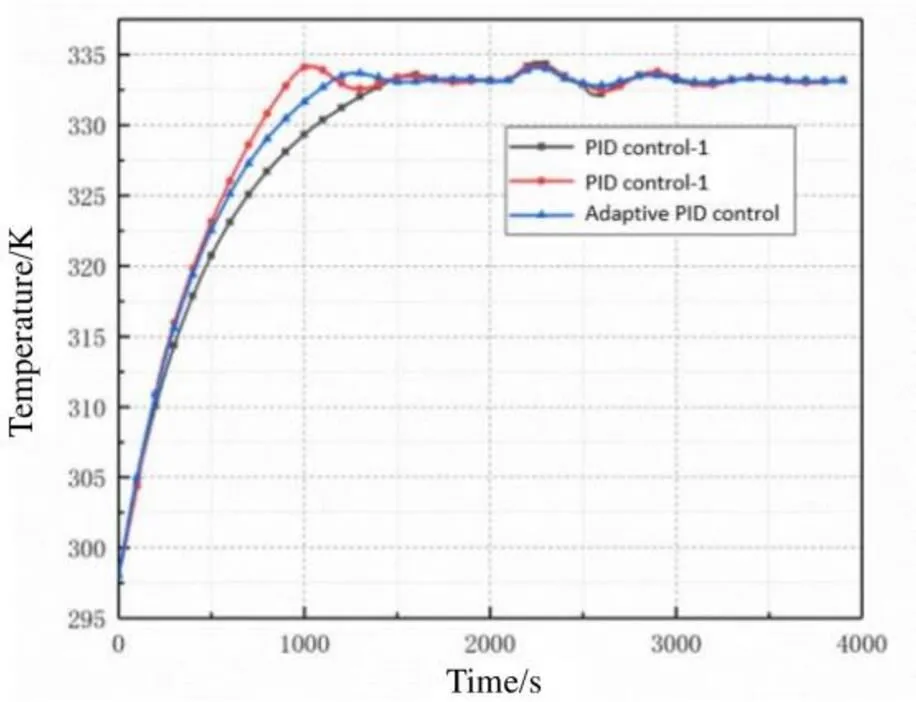
图5 实验结果对比

图5中在0时刻，保持正方体壳温度为298K不变，开启铝板控温加热，使其控温稳定在(333.15±0.1)K过程中，PID控制1所需时间为1684s，超调量为0.42K；PID控制2所需时间为1642s，超调量为1.06K；自适应PID控制所需时间小于1404s，超调量小于0.54K，控温稳定度优于±0.1K。结果表明随着被控对象温度的改变，该自适应PID控制具有更好的收敛性。

图5中在2100s时刻，铝板稳定控温在333.15K时，对正方体壳六个面分别同时加热18W，模拟空间环境外热流的大幅值增大，使正方体壳六个面的温度从298K升高至323K。铝块温度再次恢复稳定到(333.15±0.1)K过程中，PID控制1超调量为1.34K；PID控制2超调量为1.12K；自适应PID控制超调量为0.94K，控温稳定度优于±0.1K。结果表明随着空间环境外热流大幅值增大导致环境温度快速升高，控温系统的数学模型发生改变时，该PID控制器始终保持最佳动态响应，超调量小，抗干扰性更强，控温稳定性更好。

3 结论

本文从空间光机的热平衡方程出发，提出一种基于空间光机热模型的极点配置自适应PID控制方法。该方法揭示了空间光机的热模型与周围辐射换热对象的温度之间的联系，在对空间光机进行控温时，能够实时根据采集的光机及与其辐射换热对象的温度修正光机的热模型，继而采用极点配置的方法实时校正PID控制器参数，最终通过加热器实现被控对象的高稳定度温度控制，文中通过仿真及实验验证，在空间环境外热流大幅值增大导致环境温度快速升高，控温系统的数学模型发生改变时，该自适应PID控制器始终保持最佳动态响应，超调量小，调节时间短，控温稳定度优于±0.1K，具有更好的控温稳定性和环境适应性。

[1] 付家鑫. 多波段共孔径光学系统结构设计与分析[D]. 长春: 长春理工大学, 2014.

FU Jiaxin. Structure Design and Analysis of Multiband and Total Aperture Optical System[D]. Changchun: Changchun University of Science and Technology, 2014.

[2] 郑建丽. 低温光学温度测控技术研究[D]. 北京: 中国科学院大学, 2011.

ZHENG Jianli. Research on Low Temperature Optical Temperature Measurement and Control Technology[D]. Beijing: University of Chinese Academy of Sciences, 2011.

[3] 赵振明, 鲁盼, 宋欣阳. “高分二号”卫星相机热控系统的设计与验证[J]. 航天返回与遥感, 2015, 36(4): 34-40.

ZHAO Zhenming, LU Pan, SONG Xinyang. Thermal design and test for high resolution space camera on GF-2 satellite[J]., 2015, 36(4): 34-40.

[4] 李蓉. 空间太阳望远镜主光学望远镜热效应分析[J]. 航天返回与遥感, 2001, 31(12): 32-39.

LI Rong. Thermal effect analysis of main structure in space solar telescope[J]., 2001, 31(12): 32-39.

[5] Savino De Palo, Michele Cairola, Marco Compassi, et al. Herschel heaters control modeling and correlation[C]//, 2011, 4(1): 29-39.

[6] 胡旭晓, 杨克己, 台宪青. 逐级递推式超精密温度控制策略研究[J]. 机械工程学报, 2004, 40(2): 64-67.

HU Xuxiao, YANG Keji, TAI Xianqing. Research on step by step recursive ultra-precision temperature control strategy[J]., 2004, 40(2): 64-67.

[7] Taeho Keem, Seung-Woo Kim. Thermal stabilization for accurate dimensional measurement using Gallium[J]., 2004, 44: 701-706.

[8] 李国强, 耿利寅, 童叶龙. 航天器铆钟的一种精密控温系统[J]. 航天器工程, 2011, 20(4): 93-98.

LI Guoqiang, GENG Liyin, Tong Yelong. A precise temperature control system for spacecraft rubidium atomic clock[J]., 2011, 20(4): 93-98.

[9] 孟晓倩, 杨宝玉, 张家昆, 等. 机械制冷机温控的系统仿真与分析[J]. 低温与超导, 2019, 47(5): 5-10.

MENG Xiaoqian, YANG Baoyu, ZHANG Jiakun, et al. System simulation and analysis of temperature control of mechanical cryocooler [J]., 2019, 47(5): 5-10.

[10] 王伟, 张晶涛, 柴天佑. PID参数先进整定方法综述[J]. 自动化学报, 2000, 26(3): 347-355.

WANG Wei, ZHANG Jingtao, CHAI Tianyou. A survey of advanced PID parameter tuning methods[J]., 2000, 26(3): 347-355.

[11] 陶永华, 尹怡欣, 葛芦生. 新型PID控制及其应用[M]. 北京: 机械工业出版社, 1998.

TAO Yonghua, YIN Yixin, GE Lusheng.[M]. Beijing: China Machine Press, 1998.

[12] 李小亭, 韩冰, 李正坤. 关于精密控温方法的比较研究[J]. 河北大学学报: 自然科学版, 2004, 24(1): 107-111.

LI Xiaoting, HAN Bing, LI Zhengkun. Comparative study on precision temperature control methods[J].: Natural Science Edition, 2004, 24(1): 107-111.

[13] Leroy C, Maisonneuve M, Piat M, et al. Simulation of the planck-HFI thermal control system[C]//, 2008, 7017: 701713.

[14] Allidina A Y, Hughes F M. Generalized self-tuning controller with pole-assignment[J].,, 1980, 127(1): 13-18(DOI:10.1049/ip-d:19800003).

[15] 刘瑶瑶, 杨宝玉, 吴亦农. 制冷机PID温度控制参数设计[J]. 红外, 2016, 37(4): 7-10.

LIU Yaoyao, YANG Baoyu, WU Yinong. Design of PID temperature control parameters for cryocooler [J]., 2016, 37(4): 7-10.

[16] 刘伯春. 离散时间自适应控制算法的一种新统一格式[J]. 控制理论与应用, 1989(6): 59-64.

LIU Bochun. A new unification of discrete-time adaptive control algorithms[J]., 1989(6): 59-64.

Adaptive PID Control Method Based on Space Optical Mechanical Thermal Model

LI Shuai1,2，YANG Baoyu1，LU Yan1

(1.,,200083,;2.,100049,)

To improve the temperature control stability of space cameras to ensure imaging quality, an adaptive proportional-integral-derivative(PID) control method based on a space optical mechanical thermal model is proposed. The design of the controller starts from the thermal balance equation of the space optical machinery and can correct the thermal model of the optical machinery in real time according to the temperature of the optical machinery and its radiating heat exchange object. Then, the parameters of the PID controller are corrected in real time using the pole assignment method, and the heating duty cycle of the temperature control period is finally determined. In this study, by establishing an abstract thermal model of space optical machinery and applying the above self-adaptive PID control method and PID control method with fixed parameters, the effect of temperature control is compared by simulation and experiment. The experimental results show that the adaptive PID controller always maintains the best dynamic response to the temperature fluctuation caused by environmental disturbance, and the temperature control stability is better than ±0.1K; thus, the controller has better temperature control stability and environmental adaptability.

space optical machinery, thermal model, pole assignment, self-adaption, PID control

TK323

A

1001-8891(2021)10-0934-06

2020-01-16；

2020-03-16.

李帅（1992-），男，河南省南乐县人，硕士研究生，主要从事热控技术研究。

杨宝玉（1979-），副研究员，研究生导师，主要从事航天有效载荷项目中的控制电路及相关信号处理研究。E-mail：byyang@mail.sitp.ac.cn。