关于判定超欧拉图的分离结合法
陈宇龙 张 林 韦美雁 潘学文
关于判定超欧拉图的分离结合法
陈宇龙 张 林 韦美雁 潘学文
(湖南科技学院 电子与信息工程学院,湖南 永州 425199)
本文基于判定超欧拉图的收缩法和撕裂法,将两种方法进行了结合改进,提出一种新的超欧拉图的判定方法——分离结合法,并进行了实例判定。
超欧拉图;分离结合法;收缩;分裂

判定一个图是否是超欧拉图的方法最早为Catlin在1988年提出的收缩法[2]。收缩法的关键是找到有效的可折叠子图,但是在实际中对于可折叠子图的寻找十分不容易。鉴于此,我国的学者李登信提出次可折叠子图,即添加边数的方法来判定超欧拉图[3,4]。李霄民提出了撕裂法[5],即给出图的顶点的一种变换,变换保持图的顶点数不变,但边数减少;并且给出变换后的图与原图的超欧拉性的关系,从而通过变换后的图的超欧拉性导出原图的超欧拉性。本文考虑将两种方法进行结合改进,提出一种新的超超欧拉图的判定方法,把图分离成两部分,对一部分进行收缩,对另一部分进行撕裂,得到两个子图,然后连接两个子图,并引进哈密顿图的概念,实现更加快速地判定超欧拉图。我们把这种方法称为分离结合法。
1 预备知识
定义2 通过图(有向图或无向图)中所有边一次且仅一次,行遍所有顶点的回路(通路),叫做欧拉回路(欧拉通路)。具有欧拉回路的图称作欧拉图。
定义3 通过图中所有顶点一次且仅一次的回路(通路)称作哈密顿回路(通路)。具有哈密顿回路的图称作哈密顿图。
定义4 超欧拉图是指具有欧拉生成子图的图。如图1所示,黑边为其欧拉生成子图。
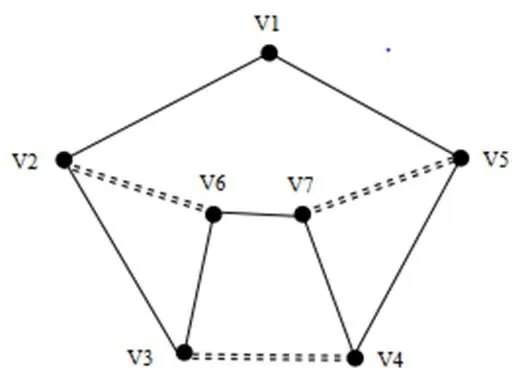
图1 超欧拉图
2 收缩法与撕裂法的原理
2.1 收缩法原理
收缩法的主要方法是找到一个比原图简单的可折叠子图。通过对收缩后获得的图的超欧拉性来引导出原图的超欧拉性,收缩法的核心在于找出可折叠子图。收缩法的判定方法及实例在文献[3]和文献[4]中有详细的介绍,本文不再表述。
2.2 撕裂法原理
撕裂法是给出图的顶点的一种变换,变换保持图的顶点数不变,但边数减少;并且给出原图与变换后的图的超欧拉性的关系,从而通过变换后的图的超欧拉性导出原图的超欧拉性。撕裂法的判定方法及实例在文献[5]中有详细的介绍,本文不再表述。
3 分离结合法
收缩法一是在可折叠子图的判定上要求太过于严格,二是对简化图的超欧拉性的判定没有涉及。而撕裂法可用于简化图的超欧拉的判定。本文考虑将两种方法结合,提高判定方法的适用性,提出一种新的方法:分离结合法。
3.1 分离结合法原理
假设图G,K是图G的一个子图,把图K分离成两部分,结合文中收缩法和撕裂法,对一部分进行收缩,对另一部分进行撕裂,得到两个子图,然后连接两个子图,并引进哈密顿图的概念,实现更加快速地判定超欧拉图。
3.2 判定方法
证明:利用反证法。
3.3 判定实例
给定案例图,如图2,现对其进行分离结合。
将图分为两部分,如图3所示,对左部分图进行撕裂,对右部分图进行收缩,重新连接得到图4(a),继续撕裂直到任意顶点的度数不大于3。如图4(b)所示。

图2 案例图
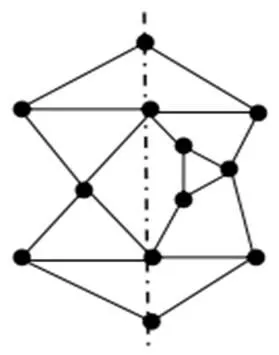
图3 分解图

图4 连接图
4 结 论
超欧拉图的判定是一个比较困难的问题,很多学者对该问题提出了一些判定方法,较好地解决了该问题。但收缩法的关键在于寻找可折叠子图,实际上可折叠子图的判定要求太过于严格,而撕裂法对于复杂图的判定太过迟缓。本文通过对这些方法的系统性研究,将收缩法和撕裂法结合起来提出了分离结合法,通过实例的判定说明使用分离结合法能够更加快速简便地判断某些图是否为超欧拉图,但对于一些简单图,如:矩形网格图的判定不如撕裂法简便。所以对于不同的图选用适合的方法更易进行判定是否为超欧拉图。
[1]F.T.Boesch, C.Suffel, R.Tindell. The spaning subgraph of eulerian graphs[J].J.Graph Theory,1977(1):79-84.
[2]Catlin P A. A reduction method to find spanning Eulerian subgraphs[J]. J.Graph Theory,1988,12(1):29-45.
[3]李登信,王斌,李霄民.关于判定超欧拉图的收缩法[J].重庆工商大学学报(自然科学版)2003,20(1):1-4.
[4]李登信,王斌. 超欧拉图的判定及Catlin-猜想的研究[J].西南师范大学学报(自然科学版)2003(1):6-8.
[5]李霄民.判定超欧拉图的一个新方法[J].西南大学学报(自然科学版)2007,29(4):41-43
O157.5
A
1673-2219(2021)03-0001-02
2021-01-24
湖南科技学院应用特色学科建设项目;湖南省教育厅2020教学改革项目(项目编号HNJG-2020-0879)。
陈宇龙(2000-),男,湖南长沙人,湖南科技学院软件工程专业2018级学生。
韦美雁(1974-),女,湖南永州人,硕士,副教授,研究方向为数据库与大数据技术、人工智能。
(责任编校:文春生)

