强风下高铁连续梁桥最大双悬臂状态抖振时域分析

谢以顺 王 浩 张 寒 高宇琦 陶天友 王飞球

(1东南大学混凝土及预应力混凝土结构教育部重点实验室, 南京 211189)(2中铁二十四集团江苏工程有限公司, 南京 210038)

预应力混凝土连续梁桥具有行车平稳、跨越能力大等优点,广泛应用于公路、铁路建设中[1],成为高铁建设中跨河、跨既有线等障碍的主要桥型.随着交通强国等国家重大战略的推进,大批高铁连续梁桥将建设于华东、华南等强风多发区.为减小桥梁建设对桥下通行、农业生产等的影响,高铁连续梁桥常采用悬臂法施工[2].在此期间,桥梁长期处于墩梁临时固结的长悬臂状态,结构刚度较小,风敏感性加剧,最大双悬臂状态下结构的抗风性能大幅降低[3].因此,需要对双悬臂状态连续梁桥开展抗风安全性能分析,以保证施工期人员、器械和桥梁结构的安全,从而有效控制施工风险.

桥梁结构在风荷载作用下会产生多种风致振动,其中颤振、驰振和涡激共振可以通过在桥梁构件的气动外形优化设计予以避免,但脉动风引起的抖振却无法避免[4].长期持续的抖振会影响桥梁施工精度,严重时可能引起结构体系破坏.在桥梁抖振分析方面,Davenport[5-6]首先将概率统计方法推广应用于桥梁抖振响应分析,搭建了经典桥梁风致抖振分析框架.Scanlan[7]引入自激力完善了桥梁风致抖振分析理论,形成了经典桥梁风致抖振频域分析框架.在此基础上,国内外学者针对斜拉桥、悬索桥等大跨度桥梁抖振分析开展了大量工作,逐步实现了大跨度桥梁非平稳、非线性抖振时频域分析[8-11].在混凝土桥梁施工期抖振分析方面,韩艳等[3]进行了连续刚构桥平衡悬臂施工阶段的抖振时域分析研究.然而,连续梁桥施工期处于墩梁临时固结状态,其结构刚度与连续刚构桥相比较小,受风荷载的影响尚不明确,且台风等极端风环境下桥梁的抖振问题愈加突出,故需对处于强风多发区的大跨度高铁连续梁悬臂施工阶段的抖振响应进行有效分析及预测.

本文以盐通高铁某大跨连续梁桥为工程背景,该桥位于华东沿海强风、台风多发区,且主跨长达132 m,最大双悬臂阶段施工安全面临重大挑战.本文依照设计参数建立了该桥施工期最大双悬臂状态有限元模型,并采用谐波合成法模拟出施工期该桥的三维脉动风场.利用时域抖振分析理论,开展了最大双悬臂状态结构抖振响应时域分析,研究了不同设计风速和风攻角对抖振响应的影响.

1 桥梁分析模型

1.1 有限元建模

本文工程背景为典型有砟单线轨道预应力混凝土单线连续梁桥.全桥布置见图1.

图1 大跨度连续梁桥全桥布置图(单位:m)

该大跨度高铁连续梁桥计算跨度为269.6 m,沿跨向布置为四墩三跨(68.8+132+68.8) m.该桥采用悬臂灌注法施工,中支点0#梁段在墩顶浇筑,其余各梁段采用挂篮悬臂浇筑,施工期墩顶临时固结,处于最大双悬臂状态时,两侧悬臂长度均为65 m.最大双悬臂状态的三维有限元模型见图2.

图2 桥梁有限元模型

1.2 动力特性分析

基于有限元模型,开展了大跨度连续梁桥施工期最大悬臂状态动力特性分析,并获取了该桥前200阶模态振型和频率.表1列出了前10阶模态频率及其振型特征.由表可知,施工期最大双悬臂状态下的结构基频为0.386 4 Hz,仅为成桥状态基频1.024 5 Hz的37.7%,说明最大双悬臂状态下桥梁刚度较小,抗风安全性较差.最大双悬臂状态下,结构第1、2阶振型出现了全桥整体摆动,第5、6阶振型出现了桥墩的弯曲模态,表明最大双悬臂状态下结构刚度较低,且整体性较差.此外,悬臂施工阶段墩梁处于临时固结状态,结构稳定性将进一步下降.因此,亟需研究大跨度连续梁桥施工期最大双悬臂状态抖振安全性能.

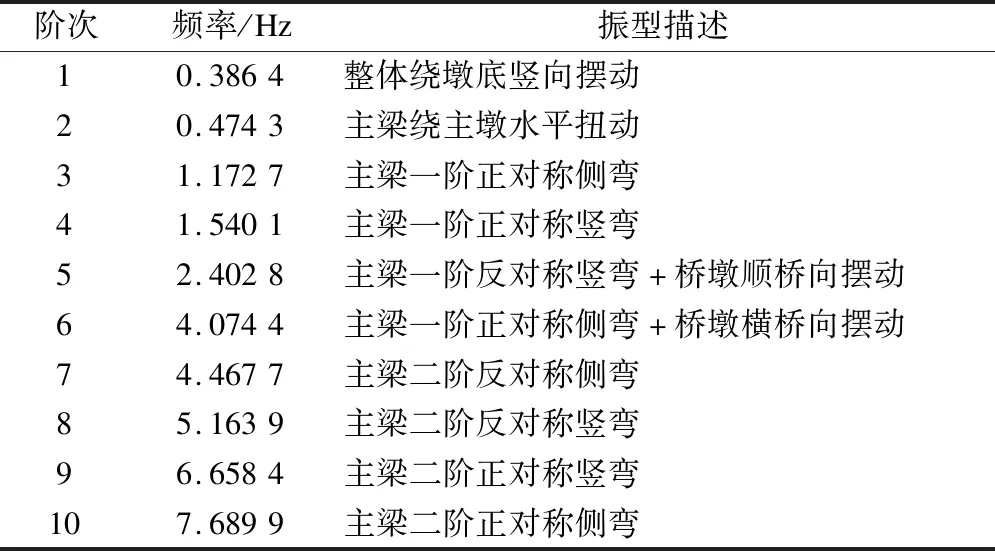
表1 大跨度连续梁桥前10阶振动模态

2 三维脉动风场模拟

参考《公路桥梁抗风设计规范》[12]中附表A.3,可确定桥址区50年一遇、100年一遇、150年一遇和220年一遇距地面10 m高处的10 min平均最大风速分别为29.5、31.7、35.1和40.2 m/s,并以此作为本文采用的设计风速.根据桥址区地形地貌资料确定地表粗糙度为B类.选取适合的风谱模型是保证风场模拟真实性和准确性的首要前提.水平顺风向及竖直方向上脉动风速的功率谱密度函数Su(n)、Sw(n)分别为[12]

(1)

(2)

(3)

式中,n为风的脉动频率;u*为气流摩阻速度;U(z)为高度z处的平均风速.由于桥面位于同一水平高度,可假定沿顺桥向分布的各点风场均相同.

基于Deodatis谐波合成法和互谱密度矩阵的显式分解[13],将规范谱作为目标谱,模拟了主梁23个模拟点的顺风向和竖向脉动风速时程.桥墩的脉动风场模拟方法与主梁类似,以式(1)为目标谱,生成了桥墩9个模拟点的顺风向和横风向脉动风速样本.主梁12#模拟点处的顺风向脉动风模拟谱、互相关函数与目标值对比见图3.由图可知,模拟风场功率谱和互相关函数均与理论值基本一致,表明所模拟风场具有较高的保真度.

(a) 功率谱

3 最大双悬臂状态抖振时域分析

作用于桥梁结构上的风荷载通常可分解为平均风引起的静风力、脉动风引起的抖振力和流固耦合引起的自激力3个部分[4].由于高铁桥主梁断面较小且整体刚度较大,主梁振动时对周围风场的影响较小,故气动自激力对抖振响应的贡献较小.本文基于Davenport抖振分析理论仅考虑静风力和抖振力来开展抖振时域分析.基于准定常理论,Davenport抖振理论框架中将脉动风作用下桥梁结构的升力表示为

(4)

脉动风作用下桥梁结构的阻力为

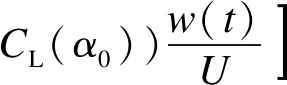
(5)

脉动风作用下桥梁结构的扭矩为

(6)

表2 主梁跨中断面三分力系数

3.1 不同设计风速下的抖振响应分析

基于谐波合成法生成了4个设计风速下高铁连续梁桥最大悬臂状态主梁和桥墩的模拟风场,并建立了风荷载模型,进行抖振响应分析.风攻角为0°,设计风速为35.1和40.2 m/s时主梁悬臂端侧向、竖向和扭转抖振位移响应时程见图4.由图可知,主梁抖振主要呈现为围绕静力平衡位置的往复随机振动.

(a) 竖向位移响应

将主梁各点处的抖振响应位移中剔除t=0时刻由静风和自重产生的静力响应部分,得到主梁各点的抖振位移响应均方根(RMS)值沿跨度方向的分布情况,结果见图5.由图可知,主梁侧向位移、竖向位移和扭转角RMS值以跨中为对称轴呈对称分布.由于主梁在最大悬臂阶段与桥墩临时固结,故3个方向的抖振位移RMS值均表现出由跨中向两侧非线性递增的规律.

(a) 竖向位移

表3给出了不同风速下主梁悬臂端位移响应峰值和RMS值.由表可知,设计风速为29.5 m/s时,主梁悬臂端最大竖向位移、侧向位移和扭转位移分别为L/1 110、L/756和L/3 196,其中L=132 m为桥梁主跨长度.对于设计时速为350 km/h的单线高速铁路连续梁桥,竖向位移已超过《高速铁路设计规范》(TB 10621—2014)[15]中L/2 500的限定.当设计风速由29.5 m/s增至40.2 m/s时,主梁抖振响应侧向、竖向和扭转位移响应峰值增幅分别为60.5%、55.1%和77.0%,位移响应RMS峰值增幅分别为48.7%、46.9%和54.9%.

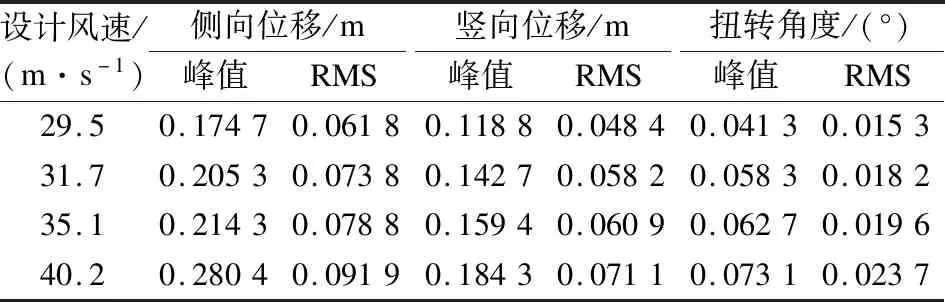
表3 不同设计风速下主梁悬臂端位移响应峰值和RMS值

3.2 不同风攻角下的抖振响应分析

由3.1节可知,当设计风速为35.1 m/s时,主梁会产生较明显的抖振响应,此时对应的重现期为150 a,满足高铁桥梁建造和运营使用年限.因此,下文中研究不同风攻角对高铁桥最大悬臂状态抖振响应的影响时,取设计风速为35.1 m/s,得到主梁悬臂端侧向、竖向和扭转抖振响应时程(见图6).剔除静力响应后,3个风攻角下主梁位移响应RMS值沿顺桥向分布见图7.

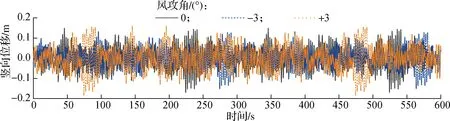
(a) 竖向位移响应

(a) 竖向位移

由图6可知,与0°攻角相比,悬臂端竖向位移响应峰值在+3°攻角脉动风作用下明显增大,在-3°攻角作用下有所下降,表明负攻角对竖向抖振位移具有一定的抑制作用.+3°和-3°攻角下侧向位移峰值相差不大.在+3°攻角脉动风作用下,扭转位移响应峰值明显大于-3°和0°攻角的情形.由图7可知,风攻角对悬臂端位移RMS值的影响与对位移峰值的影响规律基本一致.

4 结论

1) 施工期最大双悬臂状态结构基频仅为成桥状态的37.7%,结构刚度较小,抗风安全性较弱,建议在强风多发区高铁连续梁桥悬臂施工期应对结构进行抖振安全评估.

2) 50年一遇设计风速下,主梁悬臂端竖向抖振位移响应峰值达主跨长度的1/1 110,已超规范限值1/2 500,且抖振位移响应峰值随风速增加迅速增大.在强风下高铁连续梁桥施工阶段,应对最大悬臂状态抖振响应采取控制措施.

3) 与零度攻角和负攻角相比,正攻角强风作用下悬臂端抖振响应均明显增大.负攻角对主梁竖向位移有一定的抑制作用,对主梁侧向位移影响不大,悬臂施工期抖振分析应着重考虑正攻角这一不利工况.