自复位U形钢板耗能支撑设计与滞回性能分析

贾俊峰 赵凌云 白玉磊 周述美 刘 钊 李茂昌

(1北京工业大学城市与工程安全减灾教育部重点实验室, 北京 100124)(2中国建筑第八工程局有限公司, 上海 200112)(3东南大学土木工程学院, 南京 211189)

目前工程中常用的普通钢支撑结构形式简单、安装方便,但在受压过程中易发生屈曲破坏,导致承载能力和耗能能力迅速下降[1-2].屈曲约束支撑耗能能力强,具有良好的拉压疲劳性能[3-4];然而普通钢支撑和屈曲约束支撑缺乏自恢复性能,震后存在较大的残余变形.Christopoulos等[5]提出了一种由耗能系统、预应力系统和导向系统组成的自复位耗能支撑,利用摩擦装置进行耗能,以芳纶纤维筋进行复位,基本消除了残余变形.Erochko等[6]利用4个内置摩擦装置进行耗能,12根芳纶纤维筋进行复位,设计出一种高承载力自复位耗能支撑.徐龙河等[7-8]提出了一种新型预压弹簧自恢复耗能支撑,通过实验验证其具有良好的耗能能力和自复位能力.Wang等[9]提出了一种新型自复位防屈曲支撑,通过核心钢板耗能,采用交叉锚固技术提高了预应力钢绞线的变形能力,从而加倍提高了支撑的变形能力.韩强等[10]提出了内嵌碟簧型自复位防屈曲支撑,通过支撑两侧的组合碟簧提供复位力,利用一字形钢芯进行耗能,建立的恢复力模型与试验结果吻合较好.为解决现有自复位耗能支撑阻尼力恒定、起滑力大的问题,徐龙河等[11-12]提出了一种自复位变阻尼耗能支撑,利用有限元数值模拟软件,对磁场及支撑模型进行分析,探讨了支撑设计参数变化对滞回性能的影响.Qu等[13]研究了一种新型可更换U形钢板阻尼器.Taiyari等[14]设计了一种以U形钢板为耗能部件的新型支撑.Xhahysa等[15]将U形钢板应用于自复位支撑中,通过BFRP筋施加预压力,数值模拟表明支撑具有良好的耗能能力.Mashal等[16]将U形钢板组合应用到支撑中,给出了支撑在轴向载荷作用下的工作机理.然而,以上形式的自复位耗能支撑采用摩擦耗能时存在摩擦点老化问题;采用钢芯耗能时核心耗能部件难以检修和更换;采用磁流变液耗能时支撑造价较高;采用U形钢板耗能的支撑具有耗能能力强且稳定、低周疲劳性能优越的优势[17-18],且耗能部件具有可更换性.

本文提出了一种自复位U形钢板耗能支撑(SCEDB-U),采用组合碟簧提供预压力,通过U形钢板的塑性变形进行耗能.通过有限元软件ABAQUS数值模拟了该支撑的往复力学行为,分析了主要设计参数对支撑力学性能的影响.

1 力学原理

1.1 基本构造

SCEDB-U主要由传力系统、耗能系统和复位系统组成,其具体构造见图1.

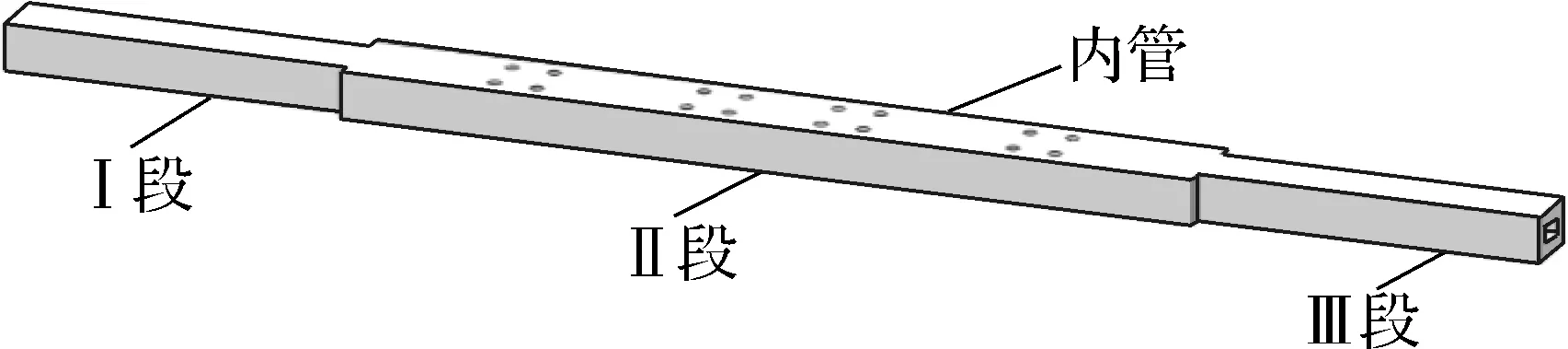
(a) 内管构造

传力系统包括内管、外管、内管挡块、外管挡块、内管导向件、左连接板和右连接板等.内管采用变截面定制钢管.穿过支撑两侧的组合碟簧时,内管充当碟簧的导向件,截面较小.中间段连接U形钢板处截面增大,以便增加U形钢板的宽度,从而增加构件的耗能能力.外管由4块钢板组成,上、下板与U形钢板连接,前、后板通过螺栓与上、下板连接,方便于后续拆卸以及检查支撑内部情况.耗能系统主要由U形钢板组成,设置在内管与外管之间,通过高强螺栓连接.复位系统主要由预压碟簧和碟簧挡板组成,碟簧受压均匀,承载力大,变形能力强.内管导向件主要用于防止内管自由端在支撑运动过程中偏离轴心位置.

1.2 工作机理

图2为SCEDB-U支撑工作原理示意图.由图可知,支撑处于初始状态时,内管、外管、U形钢板和碟簧共同为其提供较大的初始刚度.随着外力F的持续增加,当其足以克服预压碟簧提供的初始预压力时,支撑内管和外管发生相对运动.

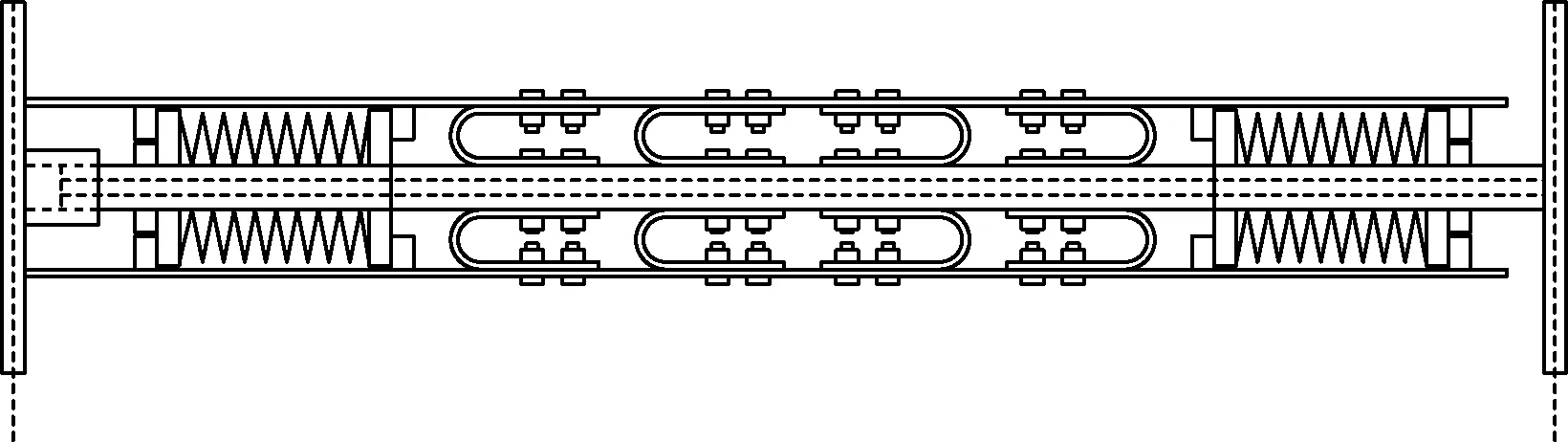
(a) 原始状态

如图2(b)所示,支撑处于受拉状态时,外管向左运动,外管第3、4挡块推动第2挡板向左运动,外管第7、8挡块推动第4挡板向左运动.内管向右运动,内管第1挡块推动第1挡板向右运动,内管右侧变截面处推动第3挡板向右运动.支撑两侧组合碟簧进一步受压,U形钢板产生弹塑性弯曲变形进行耗能.

如图2(c)所示,支撑处于受压状态时,外管向右运动,外管第1、2挡块推动第1挡板向右运动,外管第5、6挡块推动第3挡板向右运动.内管向左运动,内管左侧变截面处推动第2挡板向左运动,内管第2挡块推动第4挡板向左运动.支撑两侧组合碟簧进一步受压,U形钢板产生弹塑性弯曲变形进行耗能.

2 恢复力模型

2.1 耗能系统恢复力模型

U形钢板包含上直线段、下直线段和半圆段(见图3).图中,L、H、B、T、R分别为U形钢板的直线段长度、高、宽度、厚度和半圆段中心线半径;l为U形钢板的有效直线段长度,即半圆段和直线段连接处至螺栓孔的距离.

图3 U形钢板示意图

耗能系统恢复力模型可简化为一个双线性弹塑性模型(见图4).图中,Fe为作用在耗能系统的轴向荷载;ue为支撑两端的相对位移;Fey为耗能系统屈服强度;Fem为耗能系统极限强度;uey为耗能系统屈服时两端的相对位移;uem为支撑两端最大相对位移;Ke1、Ke2分别为耗能系统屈服前、后的刚度.

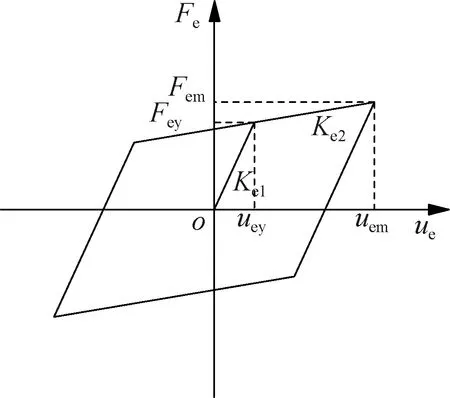
图4 耗能系统滞回模型

耗能系统屈服强度和屈服位移分别为[19]

(1)

(2)

式中,n为U形钢板块数;fy为钢材的屈服强度;E为钢材的弹性模量.

耗能系统第一刚度为

(3)

耗能系统极限强度为[13]

(4)

式中,λ、γ为材料循环加载参数,采用Q235钢材时,λ=719.8,γ=0.111.

耗能系统第二刚度为[20]

(5)

式中,β2为第二刚度系数,采用Q235钢材时,β2=2.501×10-2.

耗能系统极限位移为

(6)

2.2 复位系统恢复力模型

复位系统由支撑两端的组合碟簧构成.不考虑碟簧的摩擦耗能并采用A系列碟簧[21]时,滞回模型可简化为双线性弹性模型(见图5).图中,Fs为作用在复位系统上的轴向荷载;us为支撑两端的相对位移;Fsy为复位系统的屈服强度(此处屈服并非材料屈服,而是指由于内管和外管相对运动产生刚度变化而产生屈服点),其值等于施加的预压力F0;usy为复位系统的屈服位移;usm为复位系统的极限位移,为使碟簧一直处于弹性状态,本文取碟簧压平时变形量的75%作为极限位移;Fsm为复位系统的极限强度,取碟簧位移为75%极限压平位移时对应的支撑强度.碟簧规格、尺寸及力学指标按照规范[21]选取;Ks1、Ks2分别为复位系统的第一刚度和第二刚度.

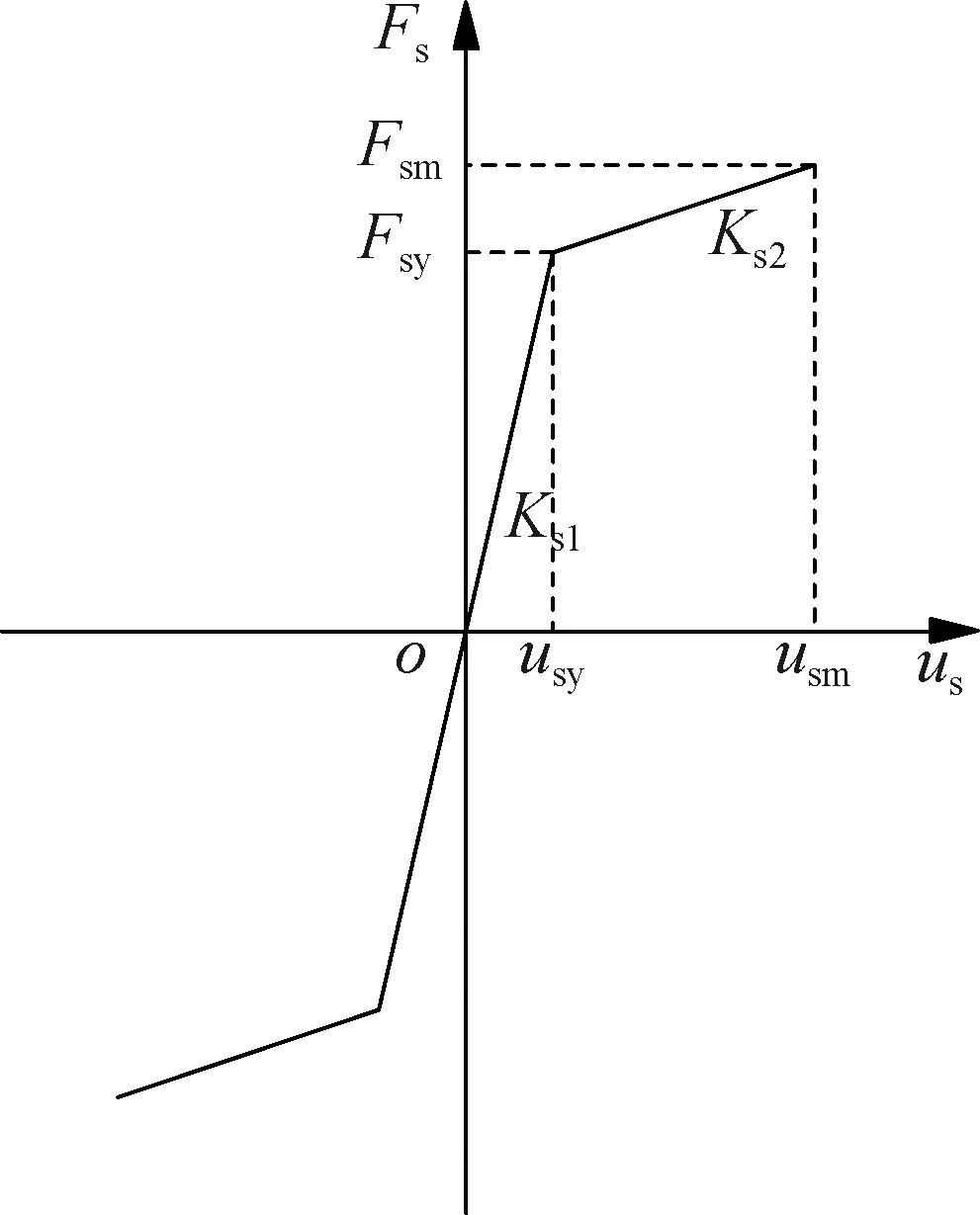
图5 复位系统滞回模型

复位系统力学模型中的屈服强度、极限强度、屈服位移和极限位移分别为

(7)

(8)

(9)

(10)

Ks2=Ks

(11)

(12)

usm=i(0.75h0-fp1)

(13)

Fsy=F0

(14)

Fsm=F0+Ks(usm-usy)

(15)

式中,A1、A2、A3分别为内管Ⅰ、Ⅱ、Ⅲ段的截面面积;l1、l2、l3分别为内管Ⅰ、Ⅱ、Ⅲ段的长度;Aout为外管截面面积;lout为外管长度;Kin、Kout、Ks分别为内管、外管和组合碟簧的刚度;Kds为单片碟簧刚度;i为单侧组合碟簧数量;h0为碟簧压平时变形量的计算值;fp1为单片碟簧预压量.

2.3 SCEDB-U恢复力模型

根据SCEDB-U的构成和受力特征,其恢复力模型由自复位系统和耗能系统的恢复力模型复合构成(见图6).

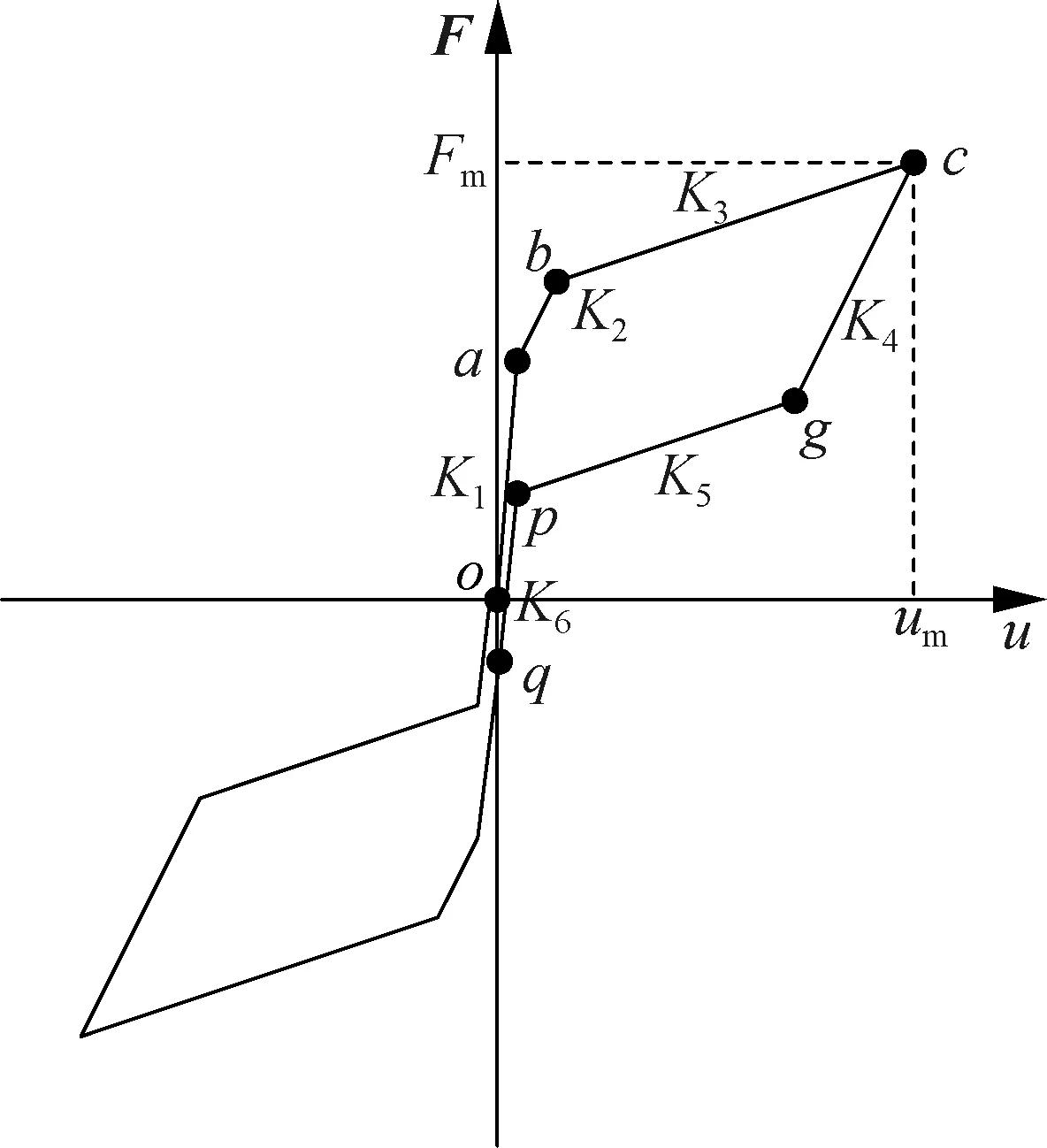
图6 SCEDB-U滞回模型

1) 开始加载至支撑内外管即将发生相对滑动阶段(图6中oa段).内管与外管串联,再与U形钢板及碟簧并联,刚度由四者共同提供.支撑在此阶段的变形主要为支撑内外管发生的弹性变形.此阶段支撑弹性刚度、恢复力、a点拉力和位移分别为

(16)

F(t)=K1u(t)

(17)

Fa=F0

(18)

(19)

2) 内外管开始发生相对滑动至耗能系统屈服前,即ab段.当外力大于碟簧预压力时,支撑内外管开始发生相对运动,相对于组合碟簧和U形钢板而言,内外管刚度较大,变形较小,可忽略其对支撑总体变形的贡献,故支撑刚度主要由组合碟簧和屈服前的U形钢板提供.此阶段支撑弹性刚度、恢复力、b点拉力和位移分别为

K2=Ke1+Ks

(20)

F(t)=Fa+K2[u(t)-ua]

(21)

ub=uey

(22)

Fb=Fa+K2(ub-ua)

(23)

3) 支撑的耗能系统由开始屈服至达到峰值承载力阶段(图6中bc段).随着外力的不断增加,U形钢板屈服,该阶段刚度由组合碟簧和屈服后的U形钢板提供.支撑最大位移由耗能系统和复位系统的最大位移值中的较小值决定.此阶段支撑弹性刚度、恢复力、c点拉力和位移分别为

K3=Ke2+Ks

(24)

F(t)=Fc+K3[u(t)-ub]

(25)

uc=min{usm,uem}

(26)

Fc=Fb+K3(uc-ub)

(27)

4) 开始卸载至耗能钢板即将屈服阶段(图6中cg段).该阶段包含耗能系统弹性卸载和耗能系统反向弹性加载2个部分,且刚度保持不变,均为耗能系统的弹性刚度.总刚度由屈服前的U形钢板和组合碟簧共同提供.此阶段支撑弹性刚度、恢复力、g点拉力和位移分别为

K4=Ke1+Ks

(28)

F(t)=Fc-K4[uc-u(t)]

(29)

ug=uc-2uey

(30)

Fg=Fc-2K4uey

(31)

5) 耗能钢板屈服至恢复完成阶段(图6中gp段).该阶段与支撑受力的第3阶段类似,刚度大小与K3相同.此阶段支撑弹性刚度、恢复力、p点拉力和位移分别为

K5=K3=Ke2+Ks

(32)

F(t)=Fg-K5[ug-u(t)]

(33)

up=ua

(34)

Fp=Fg-K5(ug-up)

(35)

6) 内外管不再相对运动,卸载位移较小(图6中pq段).由于耗能系统处于屈服状态,与第1阶段相比,此阶段支撑的轴向刚度略小.此阶段支撑的弹性刚度、恢复力、q点拉力和位移分别为

核桃是大荔县主要经济树种之一，具有较高的经济价值和生态效益，核桃除了核桃仁有食用价值外，其干、根、枝、叶、青皮都有一定的利用价值。核桃种植具有易管理，投资小，见效快，销路好，效益高等特点，是群众致富奔小康的一条好门路。

(36)

F(t)=Fp-K6[up-u(t)]

(37)

uq=0

(38)

Fq=Fp-K6(up-uq)

(39)

2.4 设计目标

SCEDB-U的设计目标为:① 保证滞回曲线的饱满性,即具有优越的耗能能力;②保证残余变形为零,即具有完全的自复位能力.结合式(35)可知,当Fp≥0时,残余变形为零.图6中p点拉力可由下式表示为

Fp=F0+Fey-Ke1usy+Ks(uey-usy)+

(Ke2+Ks)(um-uey)-(2Fey+2Ksuey)-

(Ke2+Ks)(um-2uey-usy)=

F0-Fey-Ke1usy+Ke2(uey+usy)

(40)

由于usy与uey均比较小,故可以忽略-Ke1usy+Ke2(uey+usy),则有

Fp=F0-Fey

(41)

由式(41)可知,当预压力不小于耗能系统屈服强度时,Fp≥0,即残余变形为零;否则,Fp≤0,即残余变形大于零.但考虑到以上推导是基于简化后的线性模型,而实际上钢材在循环荷载作用下会存在强化现象,滞回曲线更为饱满,且不同种类钢材本构各不相同,故建议将预压力取值为大于耗能系统的屈服强度且小于耗能系统的极限强度.

3 有限元分析

设计自复位耗能支撑构件,主要尺寸见表1.表中,D、d分别为碟簧的外径和内径;t′为有支撑面碟簧厚度.耗能系统采用8块U形钢板,复位系统采用2段组合碟簧,单侧采用18片碟簧两两对合而成,两侧总预压力为240 kN.通过ABAQUS软件对支撑的拉压往复力学行为进行数值仿真.拉压加载方式采用位移控制模式,加载幅值分别为5、10、20、30 mm.

表1 试件主要设计参数

3.1 建模及模拟结果

SCEDB-U有限元模型如图7所示.所有构件单元均采用八节点线性六面体减缩积分实体单元(C3D8R).

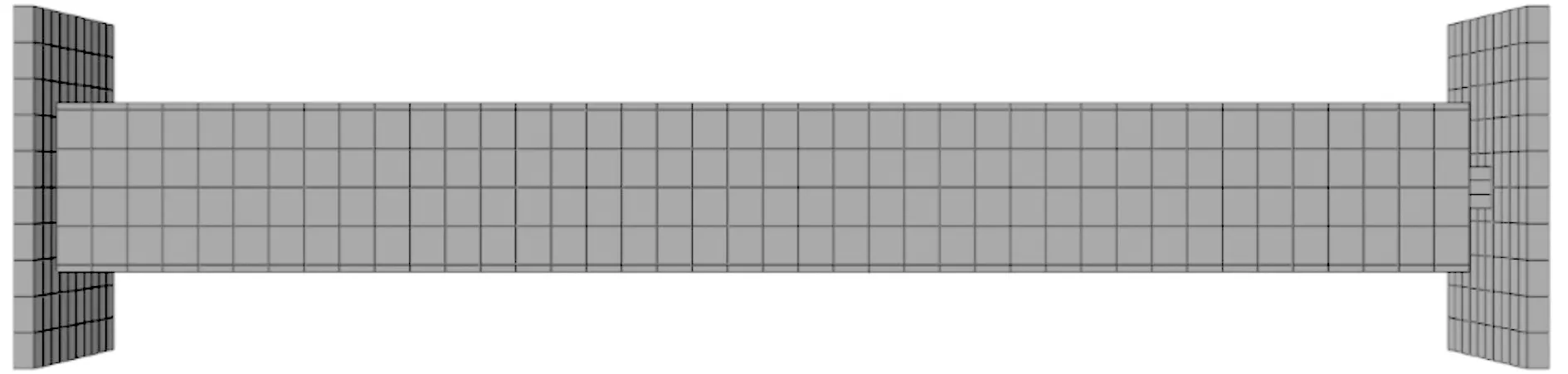
(a) 外部

U形钢板采用Q235B级钢,循环荷载作用下采用弹塑性本构模型,材性参数参考文献[22]取值.弹性阶段屈服强度为280 MPa,弹性模量为206 GPa,泊松比为0.3,钢板塑性采用混合强化来模拟,零塑性应变处的屈服应力为280 MPa,使用随动强化参数控制循环硬化,其等效应力为280 MPa,各向同性硬化应力限值Q∞=170,硬化参数b=8.U形钢板与内管和外管的螺栓连接区域简化为绑定约束,非螺栓连接区域设置通用接触.

为减少接触,提高运算效率,组合碟簧通过在两侧碟簧挡板之间建立4根并联弹簧进行模拟.根据规范[21]可计算得到单侧组合碟簧刚度为2 749 N/mm,故单根弹簧刚度为687 N/mm.组合碟簧预压力通过对碟簧挡板施加均布荷载进行模拟,预压力为120 kN,等效均布荷载为3.05 Pa.

SCEDB-U有限元模型的滞回曲线见图8.由图可知,支撑拉压滞回曲线表现为明显的旗帜形,滞回曲线较为饱满,具有良好的耗能能力;加载结束并撤去支撑轴向力以后,支撑基本实现复位,具有较小的残余变形.恢复力模型和本文模型的计算结果对比见表2.可以看出,屈服强度、极限强度的计算误差分别为11.09%和5.84%,说明本文方法是可行的.

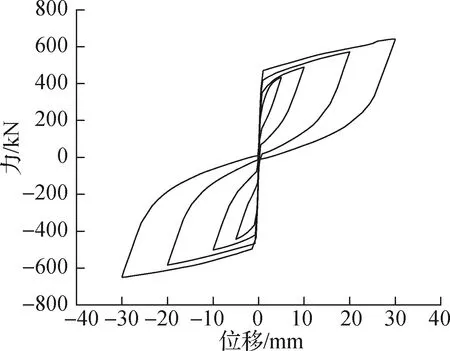
图8 SCEDB-U有限元模型滞回曲线

表2 2种模型结果对比

为探究U形钢板在加载过程中的应变变化情况,图9给出了SCEDB-U拉压过程中某一U形钢板的应变分布图.选取应变较大的某一截面,取此截面最内侧一点记为点I,中间一点记为点M,最外侧一点记为点O,并将截面定义为截面IMO.可以发现,支撑受拉时,所取U形钢板截面位置处的变形过程大致沿半圆路径发生弯曲,由于在U形钢板加工阶段该处弯曲为半圆形,故截面应变较小;支撑受压时,所取截面位置处发生拉直运动,由半圆段变为直线段,故截面应变较大.

提取点I、M、O在不同加载幅值下的最大主应变,结果见图10.由图可知,支撑受拉(正位移)时,在同一位移下,点I(即U形钢板内侧)的最大主应变最小, 点O(即U形钢板外侧)的最大主应变最大;这是因为U形钢板在运动过程中,外部卷曲程度最大,变形也最大.支撑受压(负位移)时,在同一位移下,点I的最大主应变最大,点O的最大主应变最小;这是因为U形钢板在运动过程中,内部拉直程度最大,变形也最大.

(a) 支撑受拉

图10 U形钢板最大主应变

3.2 U形钢板宽度影响分析

U形钢板宽度直接影响耗能能力的强弱.取预压力为240 kN,U形钢板宽度分别为40、80、120 mm,建立支撑有限元模型,其滞回曲线见图11.由图可知,随着U形钢板宽度的增加,支撑承载力提高,且极限强度与板宽几乎成正比,但由于耗能增加,滞回曲线的饱满程度增加,导致残余变形增大.

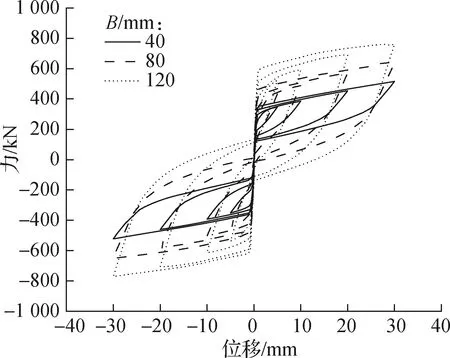
图11 不同U形钢板宽度下的滞回曲线

等效黏滞阻尼比是工程结构抗震领域衡量结构耗能能力的重要指标,其计算公式为

(42)

式中,ED为支撑滞回曲线受拉或受压半圈所消耗的能量;ES为受拉或受压最大位移下的弹性应变能.

图12给出了不同U形钢板宽度下支撑等效黏滞阻尼比.由图可知,随着位移的增大,等效黏滞阻尼比也不断增大,整体耗能稳定,拉压耗能基本对称.U形钢板宽度越大,等效黏滞阻尼比越大,支撑耗能能力越强.

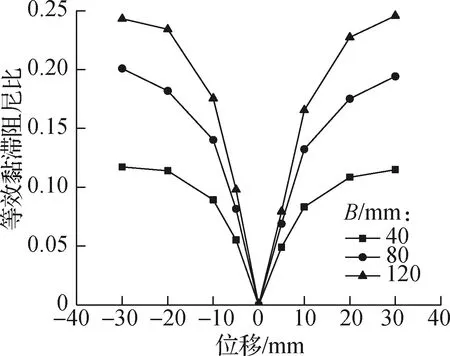
图12 不同U形钢板宽度下的等效黏滞阻尼比

3.3 组合碟簧预压力影响分析

碟簧预压力的大小直接决定了复位能力的强弱.取U形钢板宽80 mm,组合碟簧初始预压力分别为200、240、280 kN,建立支撑有限元模型,其滞回曲线见图13.由图可知,随着预压力的增大,支撑耗能能力保持不变,承载力提高且提高值约等于预压力的增量,残余变形减小,复位效果增强.

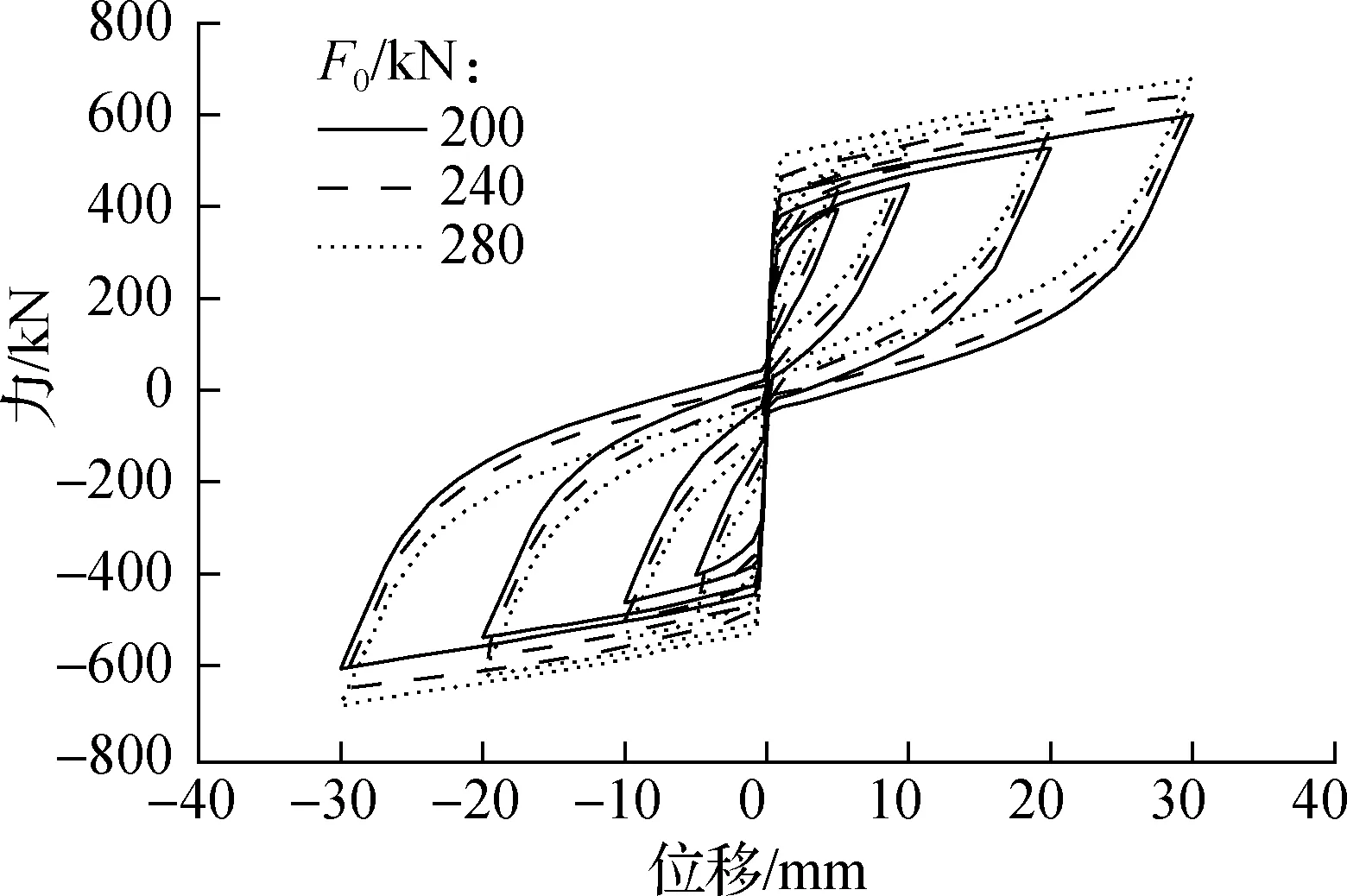
图13 不同预压力下的滞回曲线

图14给出了不同预压力作用下的等效黏滞阻尼比.由图可知,随着位移的增大,等效黏滞阻尼比也不断增大,整体耗能稳定,拉压耗能对称.预压力越大,等效黏滞阻尼比越小,支撑耗能能力相对越小.

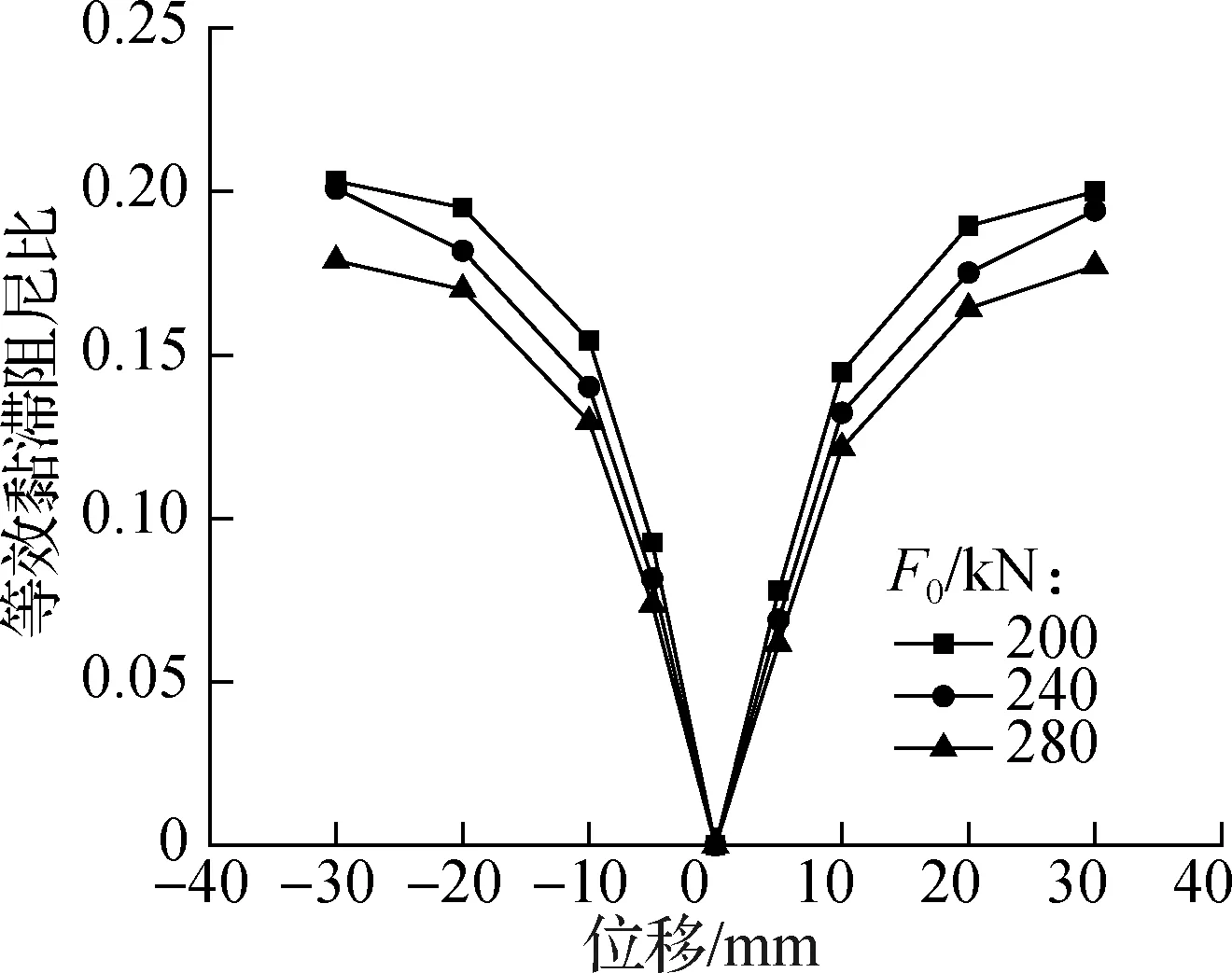
图14 不同预压力下的等效黏滞阻尼比

4 结论

1) SCEDB-U在低周往复荷载作用下呈现出饱满的旗帜形滞回曲线,受拉和受压性能对称,没有发生刚度退化和强度退化,耗能能力强,残余变形较小.

2) 屈服强度、极限强度的理论计算结果和数值模拟结果吻合较好,说明本文建立的支撑轴向力理论计算模型可以较好地预测支撑的屈服强度和极限强度.

3) 调整组合碟簧的初始预压力和改变U形钢板的参数可消除残余变形.U形钢板宽度越大,等效黏滞阻尼比越大,支撑耗能能力越强.预压力越大,等效黏滞阻尼比越小,支撑耗能能力相对越小.

4) 耗能和复位是互相矛盾、互相削弱效果的组合过程.为使SCEDB-U支撑同时具有较好的耗能和复位效果,建议将组合碟簧的预压力取值为大于耗能系统的屈服强度且小于耗能系统的极限强度.