开放题的解题技巧在初中数学教学中的应用

吴淑娟

(江苏省南京市文枢初级中学 210000)

随着新课改的不断推进，在初中数学教学的过程中，不仅需要将基础知识传授给学生，同时还需要对学生的核心素养进行有效培养和提升，因此也就需要数学教师能够在实际教学过程中，重视学生数学思维的发展，以及综合运用数学知识解决问题能力的形成.而开放题的出现，为数学教师培养学生这一重要的发散性思维能力提供了良好的教学方向，教师可根据此类题型，指导学生研究相应的解题技巧，有效锻炼其发散性思维能力与数学题解题能力.

一、初中数学开放题提出的要求

初中数学教学过程中，开放题占的比重越来越大，其最为明显的特点就是多种解题方法或者答案不唯一，让学生能够在解题的过程中自主从多个方向思考分析问题，寻找不同的解题思路，获取不同的解决方法和解题技巧，旨在帮助学生拓展思维模式，培养创新能力.这一创新题型的出现，让初中数学教学内容和教学方式都开始出现变化，对教师的教学和学生的学习提出了相应的要求.

首先，数学开放题的解答对学生的基础数学知识把握能力提出了要求，强调了教师在教学指导的过程中，要着重加强学生对基础知识的有效把握，这可从根本上提高学生的开放题解答能力.其次，数学开放题对学生的多元解题能力提出了要求，教师需在教学过程中培养学生多角度思考问题解决方法的良好学习能力，探索开放题的多样化解题方式.最后，数学开放题的解答对学生的灵活、综合运用知识能力等都提出了要求，教师在开放题教学中应指导学生对数学知识进行有效的融会贯通与灵活运用.

由此看来，初中数学教师应将开放题的解题训练作为重要的教学内容，着重夯实学生的数学知识基础，提高学生的发散性思维与多元解题思维能力，并且提升学生的知识运用能力，保障学生在开放题解题训练中获得充足的个性化发展.

二、初中数学开放题训练的重要性

在以往的数学教学中，教师为学生设计的数学习题具有一定的封闭性，不少习题都只有唯一的标准答案.而开放题却与之相反，具有较强的开放性，解答的方法和答案都具有不确定性.在数学教学改革的背景下，初中数学教师开展开放题训练，指导学生掌握好开放题的多种解题技巧，这对于促进学生的健康发展有着重要意义.

一是开放题解题训练可突破学生的固定思维束缚，让学生逐渐建立起新型的数学学习思维模式，使其数学学习过程和学习方法都焕然一新.二是开放题解题训练可让学生不再过于被动地进行数学学习，懂得主动探索和推敲数学题的解题过程，有利于增强学生在开放题解答过程中的解题思维活力，同时也可有效增强学生在开放题解题训练中的自主学习和探究能力.三是开放题解题训练可促进学生的知识应用能力的发展，并懂得创新自己的解题方法，学会吸纳其他有用的数学知识来检验开放性问题的可操作性，让学生建立起新的数学知识框架.

为了促进学生在数学解题教学中的健康发展，教师应将开放题作为重点训练的内容，指导学生掌握好开放题的多种解题技巧.

三、初中数学开放题的解题技巧分析

1.抓住涉及的基础知识点促使学生掌握解题技巧

数学开放题涉及到的数学知识范围一般比较广泛，体现了较强的综合性特点.教师开展开放题的解题训练，其中一个关键的教学目标就是要锻炼学生对数学知识点的灵活、熟练运用，让学生不再只是停留在掌握单一知识点的学习层面上.因此，数学教师要增强开放题的解题训练效果，让学生掌握好开放题的解题技巧，其中一个最根本的做法就是抓住开放题可能涉及到的基础知识点来展开思考，建立起开放题的解题思路，让学生从这个角度入手，高效掌握好开放题的解题技巧，提升学生对数学开放题的解题水平.

例如，教师给出了这样的一道开放性试题：已知二次函数图像上有三点，分别是(-1,0)、(3,0)、(1,4)，则它的函数关系式是____.学生在解答这类开放性试题时，可抓住其中涉及到的基础知识点，寻找相应的解题思路.除了常规的设二次函数一般式y=ax2+bx+c，用三元一次方程组求解函数关系式以外，还可以根据题目中(-1,0)和(3,0)这两个点的坐标特点，利用二次函数的图像特征，利用交点式的解题思路进行解答：因为学生已经学过“坐标”相关的基础知识，所以可以知道(-1,0)和(3,0)这两个点均在x轴上，因此学生可以利用交点式进行假设，即y=a(x+1) (x-3)，再将(1,4)代入关系式中，可求出a的值为-1,即所求的函数关系式是：y=-(x+1) (x-3).

本题通过让学生观察点坐标的特点，结合二次函数关系式的特点，能够促使学生对所学基础知识进行灵活运用，方法多样化，进而有效提升学生运用所学知识的能力，活跃学生的数学解题思维，优化解题方法.

2.让学生通过合理猜想与验证方式掌握解题技巧

在初中几何题的训练中，合理猜想与验证的解题方式是比较常见的，尤其是当学生遇到了结论开放的题目，则可通过合理猜想与验证的解题方式来展开思考，寻找解题的有效方法与技巧.而且这一学习方式对学生的逻辑思维与发散思维提出了一定的要求，教师可根据具体的、有针对性的开放题来展开这方面的习题训练，以提高学生对数学开放题解题技巧的掌握程度.

图1

例1如图1，在△ABC中，点D在BC边上，点E在AC边上，∠B=30°，AD=BD，DE=CE，如果A、D、E三点所组成的图形为等腰三角形，求∠C的度数.根据题意，学生可以进行分析：在△ABD中，由AD=BD、∠B=30°，可得∠ADC=60°；在△CDE中，由DE=CE，可得∠C=∠EDC；由△ADE为等腰三角形，教师可以带领学生进行分类猜想.再利用假设∠C=x°,则∠ADE=(60-x)°, ∠AED=2x°,∠DAE=(120-x)°,分别讨论当AE=AD、DA=DE、EA=ED时x的值，从而验证得出：∠C的度数是20°或40°.

本题让学生运用分类思想猜想等腰三角形的三种情况，再结合严谨验证来解决问题，训练过程中让学生自主探究，并在此过程中提升逻辑思维能力和发散性思维能力.

3.在开放性习题训练中渗透一题多解的解题理念

在初中数学的开放题训练中，教师可适当地为学生渗透一题多解的多元解题理念，有利于学生树立起良好的一题多解的创新解题意识，也可帮助学生在开放性习题训练的过程中提高自己的一题多解解题能力.

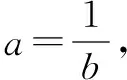
开放题已经成为初中数学考试中比较常见的试题类型，教师要提高学生在数学考试中的成绩，则必须要注重加强开放题的习题训练，让学生通过有效的开放题习题训练，掌握好开放题的各种解题技巧，提高初中生的数学思维能力和开放题解题能力.