基于机扫雷达对海模式下的数据处理策略
李 萌 王 博
(西安长远电子工程有限责任公司 西安 710100)
0 引言
由于海洋探测环境较为复杂,对海雷达目标检测与跟踪技术面临较多的局限性。尤其是杂波的干扰,不仅包含海杂波、气象杂波等不同杂波种类,而且不同海情下的杂波分布具有极大的差异。此外,海面目标的运动速度较慢,雷达对其方位上的探测误差较大,使得目标的运动趋势难以获取。提高目标跟踪的稳定性和准确性是海上雷达亟待解决的关键问题。
在信号处理层面,一般采用动目标显示(MTI)、动目标检测(MTD)、恒虚警(CFAR)等方法抑制杂波[1]。但是,这些方法不能完全消除杂波,给数据处理带来较高的误报率,可能会导致误航迹的产生。另外,当目标航迹在海上开始起批时,使用逻辑法不能很好地抑制杂波,造成了大量的假航迹。在传统的海上监视雷达数据处理中,卡尔曼滤波方法由于检测精度低,无法消除航迹抖动。
针对这些问题,本文提出了一种基于机扫雷达的数据处理策略,并针对海面目标的特点进行了适当优化。
1 对海模式下的数据处理策略
雷达数据处理是指雷达接收到信号处理上报的点迹后,进行相应的处理获得目标航迹的过程,主要包括航迹起始、航迹关联、滤波跟踪等模块。雷达工作于对海模式时,数据处理的各模块需结合海上目标的特点选取合适的处理方法。
基于Hough变换的航迹起始算法可以在密集环境中有效起始目标航迹,但其需要的时间长;基于逻辑的航迹起始算法虽然能在较短时间内起始航迹,但在密集杂波环境中则很难起始目标的航迹。针对海杂波引起的虚警,结合海面目标直线运动的特点,可采用基于Hough变换和逻辑的航迹起始方法,将两种算法结合起来,可有效解决上述问题。
数据关联是跟踪滤波的前提,也是数据处理的基础。概率数据关联算法(PDAF)的原理较为简单,算法的复杂度较小,利用PDAF对杂波环境中的单目标进行跟踪的优点是误跟和跟丢的概率较小,因此选用PDAF完成目标跟踪。
本文利用改进的卡尔曼滤波算法实现对海上目标的跟踪。根据海面目标的运动趋势较为稳定的特点,采用卡尔曼滤波算法进行滤波跟踪,之后进行时域平滑处理。该数据处理策略可快速有效地建立稳健的航迹,提高海上目标的跟踪精度,适用于实际工程应用。
2 对海目标数据处理模块实现
2.1 基于Hough变换和逻辑的航迹起始
海杂波通常会带来高虚警,并且雷达对目标方位上的探测误差较大,结合目标运动状态稳定、直线运动的特点,可采用基于Hough变换法的航迹起始。同时为了能够快速起始航迹,本文采用基于Hough变换和逻辑的航迹起始算法。
考虑到海面目标一般是匀速运动的,若选用位移-时间作为参量,则海面目标运动可看作直线运动。因此选用时间-斜距数据进行Hough变换[2],得到候选航迹。
Hough变换直线检测原理如式(1)所示。
ρ=rcosθ+tsinθ
(1)
将t-r平面中的所有点映射为θ-ρ平面中的一条曲线;通过判断θ-ρ中各点的积累程度完成对t-r平面内直线的识别和检测。
设海面目标的所有量测点数据为(tk,rk),k=1,2,…,N,由于海面目标的量测误差大,这里宜选择比较大的Δθ。经过Hough变换后,量测点在θ-ρ平面对应的曲线相交于同一点,经过积累阈值判断提取出相应的候选目标航迹。
经过Hough变换的点迹粗关联后,大量杂波点已被剔除,对于出现的点迹与点迹互联模糊的情况,采用基于3/4逻辑法的航迹起始方法进一步进行点迹的关联[3]。构成可能航迹的点迹数据必须满足速度选通的条件, 如式(2)所示。
(2)
式(2)中:Δx为相邻时刻两点的距离差;Δt为相应的时间差;Vmin为海上目标的最小速度;Vmax为海上目标的最大速度。
此外,为防止低空目标航迹起始中的点迹关联错误,还需在3/4逻辑法加入满足高度限制的条件
Δh (3) 式(3)中:Δh为待关联的点迹与待起始航迹中最后一点的高度差;R为待起始航迹中最后一点的斜距;Δθ为俯仰测角精度;λ为系数,一般取λ=3。 跟踪滤波是海面目标跟踪过程中最为关键的问题,由于目标背景噪声起伏以及目标运动特征的不确定性,需要针对其运动特性对跟踪滤波算法进行适当的优化改进。 海面目标的运动状态稳定,可看作匀速行驶,因此对其进行跟踪滤波的关键在于如何降低雷达对目标的量测误差。若采用标准的卡尔曼滤波算法,得到的航迹将会抖动较大,并且一般来说,抖动程度与目标距离成正比,与目标速度成反比,大大降低了雷达对海上目标的跟踪精度和稳定性。针对此问题,本文提出相应的跟踪滤波优化方法如下: 1)采用最小二乘曲线拟合法对目标的轨迹进行拟合,预测下一量测点位置,根据此预测值进行卡尔曼滤波; 2)利用多个量测点的方位信息进行时域平均以平滑目标量测的方位向抖动。 2.2.1 航迹拟合 海面目标的航向和航速是相对稳定的,其轨迹通常是光滑的[4],根据海上目标的运动状态较为稳定的特点,采用卡尔曼滤波算法进行滤波跟踪,之后进行时域平滑处理,得到目标航迹。 利用回归分析的方法来获取目标航向,具体表述为:对雷达量测数据进行拟合,目标航向即为对拟合后的方程求取的导数。出于工程实用性,采用最小二乘曲线拟合法,取M个量测点来拟合得到目标的轨迹方程[5]。拟合的精确度与M值成正比,计算量也与M值成正比,因此M值并不是越大越好,其选取准则与目标机动情况相关,如果目标运动状态稳定,可以选取较大的M值,增强算法鲁棒性;如果目标发生机动,则应当选取较小的M值,增强算法的灵活性。采用一阶拟合方程为 y(x)=a0+a1x (4) (5) 求出使E最小的(a0,a1),即根据式(6)求函数E的极小值点为 (6) 拟合后的观测序列可表示为 yi=y*(xi)+εi (7) 式(7)中,(xi,yi)为量测值在直角坐标系下的坐标,y*(xi)是yi的拟合估计值,εi为拟合值与真实值之间的误差。 根据拟合后的轨迹,计算最后一个点迹在拟合方程中的导数,即航向的估计值θk为 (8) 根据当前的航向θk预测下一量测点位置X(k+1|k),之后根据此预测值进行卡尔曼滤波。 2.2.2 时域平滑 上文航迹拟合过程可视为空间上的平滑处理,经过该步骤后,目标航迹趋于稳定,此时对处理后的航迹继续进行时域上的平滑处理可以得到更为稳定的航迹,提高雷达对海上目标的跟踪精度和航迹稳定性。 在探测距离远造成目标方位量测的误差较大的情况下,对其方位角采用时域平滑处理:利用目标当前时刻方位值和航迹中前M个时刻的量测点方位角信息进行平均,以该平均值作为当前时刻目标的方位角估计。其中,如何选取M值的准则和航迹拟合中M的选取准则相同。 工程实现中,航迹拟合是为建立较好的跟踪处理模型做准备,时域上的平滑是为了更直接地消除航迹抖动,这两种策略均可改善海上目标航迹的精度和稳定性。 试验时所使用的雷达系统采用X波段、脉冲多普勒体制。该系统主要由雷达主体、显控终端两部分组成,雷达主体和显控终端以网线连接。其中,雷达主体包括天线阵面、收发机、信号处理机等,主要负责发射/接收电磁波信号,并对回波信号进行放大、变频、A/D采样、匹配滤波、动目标检测、恒虚警处理,输出目标及其点迹航迹;显控终端主要负责对目标点迹航迹进行显示,并根据需要对雷达进行参数设置和远程控制。 试验时雷达架设于某海边高地附近,对往来船只进行探测跟踪。所架设的雷达系统如图1所示。 图1 试验时的雷达架设图 采用本文的数据处理策略,使用雷达对高地附近主航道上的船只进行探测。在显示控制终端上可以清楚地观察到多条船只航迹,且均能与船舶自动识别系统(Automatic Identification System, AIS)数据吻合。试验验证,雷达可实现对70km内海上目标的检测和跟踪,试验时航迹效果图如图2所示。 图2 对海试验航迹效果图 雷达的探测距离越远,探测精度越低,目标的跟踪难度越大。反映在显示终端上的现象是:距离越远的船只,航迹抖动幅度越大。本文提出的针对航迹抖动的优化策略可有效解决此问题,相关航迹的滤波精度分析如下。 令(rship,θship)表示某时刻雷达探测到的船只目标信息(r为距离,θ为方位角),令(rAIS,θAIS)表示该时刻雷达探测到的船只目标在AIS设备上的对应信息(r为距离,θ为方位角)。则距离均方根误差(RMSE_r)、方位角均方根误差(RMSE_θ)可以定义为 (9) (10) 式(9)、式(10)中,N为目标航迹点数。 针对航迹抖动的优化前后的某条航迹的跟踪滤波均方差如表1所示。 表1 优化前后航迹的滤波精度 根据表1中数据的对比情况可以看出,本文提出的优化策略对航迹的平滑效果显著,可以实现海上目标的稳定跟踪。 本文提出了基于机扫雷达对海工作模式下的数据处理策略。出于工程实用性的考虑,针对海面目标机动较小、直线运动的特点,本文采用基于Hough变换和逻辑的航迹起始方法,在快速有效起始目标航迹的同时减少了虚假航迹;本文提出的相关优化策略可有效解决雷达探测远距离海上目标时出现的航迹抖动问题,并提高海上目标航迹的稳定性。通过雷达对海试验验证,此数据处理策略可以实现对海上目标的稳定搜索和跟踪。2.2 针对航迹抖动的滤波优化
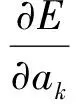
3 试验结果分析
3.1 雷达系统介绍

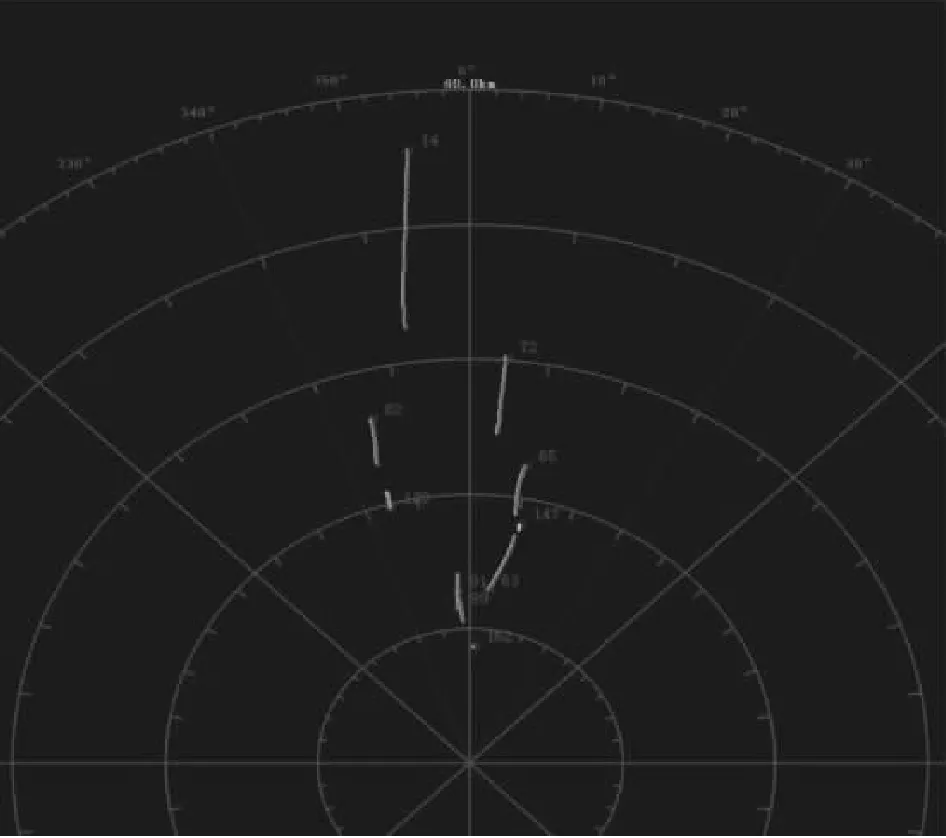
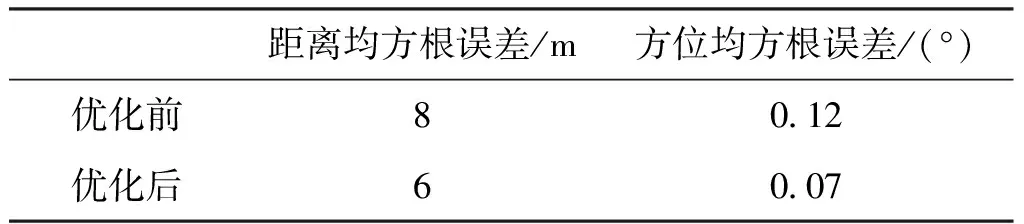
3.2 实测数据分析
4 结束语

