偏正态数据下众数混合专家回归模型的参数估计
王格格,鲁钰,吴刘仓
(昆明理工大学理学院,云南昆明650504)
1.引言
在我们的现实生活中收集到的数据大多数都不具有严格的对称性,而是具有一定的偏斜,如果我们继续用对称分布比如:正态分布、t分布、Laplace分布等进行统计推断可能会得到不合理甚至错误的结论.因此,对偏态数据的统计推断成为统计学研究的一个热点问题.在偏态数据中,众数比均值、中位数应用更为广泛,在总体中,众数标志着出现次数最多,它刻画了总体数据集中趋势的大多数水平.为了更好地拟合偏态数据,捕捉到更全面、更准确、更及时有效的信息,本文针对偏正态分布建立了众数回归模型,进一步拓展了偏正态分布下众数混合专家回归模型.
偏正态分布作为正态分布的推广,不仅具有正态分布的良好统计特性,同时也有具有偏态分布的特征,适用性更广泛,所以国内外许多学者研究了偏正态分布问题.Azzalini[1]首先研究了偏正态分布及其累积分布函数和概率密度函数的性质;万文等[2]研究了偏正态分布下联合位置与尺度模型的统计诊断;马婷等[3]研究了基于偏正态分布联合位置,尺度与偏度模型的极大似然估计;朱志娥等[4]在未对混合比例建模的情况下,研究了偏t正态数据下混合线性联合位置与尺度模型的参数估计;Lachos等[5]在多元偏正态回归模型上,基于EM算法构建多元偏正态回归模型的极大似然估计;在变量选择方面,吴刘仓等[6]基于偏正态分布研究了联合位置与尺度模型的变量选择问题;LI和WU等[7−8]分别基于SN、StN分布,对联合位置、尺度和偏度模型的参数估计和变量选择做了研究.但上述研究仅对偏正态分布或偏正态分布的位置和尺度进行建模,没有考虑数据来自异质性群体.
在经济金融、环境工程、生物医学等领域的实际问题中,经常遇到异质总体数据.数据越来越复杂对统计建模有更高要求,传统的单一模型难以对异质总体数据得到较好的拟合效果,因此发展了混合回归模型.在异质总体中,混合专家回归模型是最重要的统计分析工具之一,用来对异质总体数据进行分类及回归分析,在统计机器学习方面应用广泛.混合专家回归模型首先由Jacobs等[9]提出,对部分密度函数建模的同时,还对混合比例进行建模;随后,Yuksel[10]对混合专家模型及其性质进行了详细的描述;最近,Chamroukhi等[11]针对混合回归专家模型提出了一种基于t分布的稳健模型;吴刘仓等[12]研究了基于偏正态分布下联合位置与尺度混合专家回归模型的参数估计.
目前,基于偏态数据和混合专家回归模型的研究现状可以发现,虽然偏正态分布和混合专家回归模型都已经有了很多的研究成果,但在混合专家回归模型的框架下对偏态数据下众数建模涉及较少.考虑到混合专家回归模型在实际问题应用中的重要性,本文建立了偏正态分布下众数混合专家回归模型,并对该模型进行参数估计,通过随机模拟和实例结果表明本文提出的模型是具有可行之处的.
本文的组织结构安排如下:第二部分分别介绍了偏正态分布、偏正态分布下众数回归模型及其混合专家回归模型;第三部利用MM算法和基于梯度下降法的EM算法分别对各个模型的参数进行估计;第四部分通过MonteCarlo模拟证实本文提出方法的有效性;第五部分使用了澳大利亚身体质量指数(BMI)数据中的一个实际例子来说明本文提出的模型和方法的效果;最后是本文的小结部分.
2.偏正态分布下众数混合专家回归模型



图1.混合数目为2的混合专家回归模型


3.参数估计





III 确定混合数目
在上面的讨论中,我们假设m是已知的,处理方法要么是基于先验信息,要么是对数据进行预分析.可逆跳跃马尔科夫链蒙特卡罗(RJMCMC)(见文[20])是一种可行的算法,由于增加了偏度使算法变得复杂,我们没有继续使用RJMCMC.此外,贝叶斯推断混合建模中评估的成分后验概率可以用作一种软聚类方案.另外,可以使用对数似然估计和两个基于信息的准则,AIC[21]和BIC[22]来确定混合数目.众所周知,模型选择标准方面已经取得了一些成功,但为混合模型选择正确的混合数目是有一定困难的.
为了提高本文选择混合数目的效率,采用了一种通过众数识别的生产性聚类方法[23].这种方法在高维空间和数据的分布偏离高斯分布的情况下是稳健的.具体来说,这些样本点上升到密度函数的同一局部最大值形成一个聚类,并利用两个聚类密度凸点之间的脊线定义了聚类的两两可分性测度.在此过程中,采用模态EM(MEM)算法和脊线EM(REM)算法.水平5时集群数量依次为37、10、4、2、1.我们在第5节中演示了水平2和水平4时的聚类结果.
4.Monte Carlo模拟


表1.模拟估计结果
从表1可以得出结论,随着样本量n增大,参数估计值均越来越接近真值,且估计的均方误差MSE均逐渐减小,说明样本量越大估计效果越好.
5.实例分析
现实生活中,我们通常要根据研究对象的特征对其进行聚类分析,如果只是对样本进行总体上的分析,得到的结果可能是不准确的,如果能将总体分成具有相似特征的若干个子聚类,对每个子聚类进行分析,得到的结果可能比仅对总体分析更接近实际.在本节中,我们利用澳大利亚体育研究所收集的100名女性和102名男性运动员的体质指数(BMI)数据来说明本文提出模型和方法的实际应用.
人体体质指数由身高和体重计算得到的,但跟身体其它机能有密切关系,该数据包含一个响应变量Y −体质指数(BMI)和四个解释变量:X1−白细胞计数;X2−血浆铁蛋白浓度;X3−皮肤褶皱总和;X4−体脂百分比.总数据的BMI直方图(见图2)是右偏的,如果我们用正态分布来拟合,会有一些样本点被视为异常值,因此,我们使用本文所提出的模型和方法进行深入分析.我们通过3.3节的方法来确定混合的数目,结果如图3所示.当处于水平2时,形成了10个集群,如图3(a)所示.图3(b)和(d)为水平2时的10个集群在水平3时合并为4个集群.与水平4时相比,水平3的第1类和第2类中排除了两个有影响的观察结果.这里,水平2时的10个集群其对应的大小(包含的点的数量)分别是95、48、33、18、3、1、1、1、1、1.为简单起见,我们考虑以下模型:
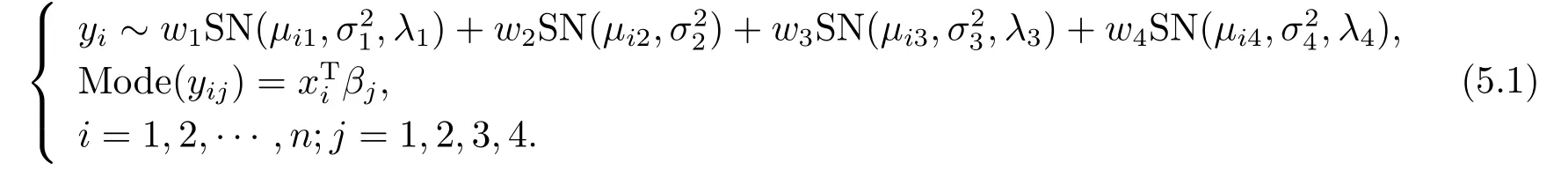
其中,µij由(2.7)定义.xi是一个4×1 向量,由所有4个潜在变量组成.
我们采用本文介绍的梯度下降法辅助的EM算法得到参数估计的最大值,结果见表2.显然,含四个成分的模型的对数似然估计最大,AIC和BIC值最小,所以这个模型是最优的.模型在水平2时,体脂百分比(x4)在第2组和第4组中更易获得较高的BMI指数,血浆铁蛋白浓度(x2)只在第1组中有助于达到较高的BMI指数.
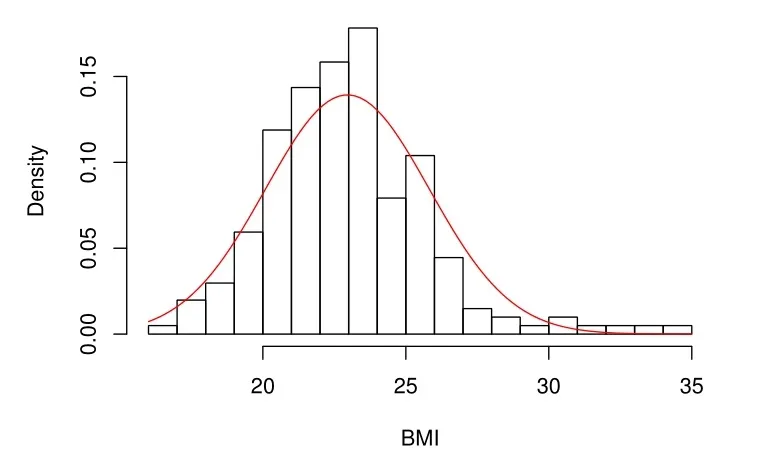
图2.总体数据的BMI直方图

图3.对获得的BMI数据聚类;(a)为水平2时聚成10类;(b)为从水平2到水平3时的上升路径;(c)为水平3时聚成5类;(d)为水平3到水平4时的上升路径;(e)为水平4时聚成2类;(f)为水平4到水平5时的上升路径
6.结论
本文建立偏正态分布下众数混合专家回归模型,目的是估计异质总体的不同回归参数,而不是对总体参数的单一估计.并且对混合比例建模,对影响混合比例的解释变量有一定了解,在实例中有很好的体现.
Monte Carlo模拟表明本文提出的MM算法和梯度下降法辅助的EM算法对偏正态分布下众数混合专家回归模型未知参数进行了较好的估计.与现有的模型和估计方法相比较,提出模型有较好的灵活性,不仅把各异质总体所占比例估计出来,同时也能估计异质总体的回归参数.此外,为确定混合数目,我们采用文[23]提出的方法来聚类,取得了良好的性能.表明,本文提出的模型和方法是有效可行的.
- 应用数学的其它文章
- Global Boundedness and Asymptotic Behavior in a Chemotaxis Model with Indirect Signal Absorption and Generalized Logistic Source
- Performances of Preliminary Test Estimator for Error Variance Under Pitman Nearness
- 一类梯度自然增长的拟线性椭圆型方程分布正解的存在性与多重性
- 一类由原根生成的伪随机子集
- 混合次分数布朗运动下永久美式回望期权的定价
- 双水平控制策略和延迟不中断单重休假的M/G/1排队系统分析

