液压电磁式脱扣器电磁系统瞬态热分析

苏秀苹，程浩峰，施宏伟，付 哲

（1.河北工业大学电气工程学院 省部共建电工装备可靠性与智能化国家重点实验室，天津300130；2.浙江百事宝电器股份有限公司，浙江 丽水323000）

1 引言

设备用断路器是我们最常用的低压电器之一，其多采用液压电磁式脱扣器作为核心部件，由于其保护特性精度高、适应高低温环境、功耗低，特别适用于通信设备、铁路信号设备及各种自动化设备的过载与短路保护［1］。虽然液压电磁式脱扣器中的采用的甲基硅油性能稳定，但是温度还是会引起其粘度的变化，从而导致断路器脱扣性能的改变［2］。到目前，关于不同环境温度下液压电磁式脱扣器工作特性的理论研究很少。

为了提高断路器的保护特性，因此对断路器的操作机构、整体模型的等方面进行了深入研究［3-5］。而在温度场分析方面，文献［6］建立了小型直流电磁继电器热电耦合分析模型，得到了继电器各部分的温度场。文献［7］对电连接器进行热分析和振动分析，得到了结构的温度云图。文献［8］对油阻尼断路器接触系统的热特性与电磁部分的热特性，进行了稳态温度场分析。文献［9］运用ANSYS软件对继电器进行了反复短时工作制下的瞬态温度场计算，根据结果总结出了瞬态温度场的分布规律和影响因素。

在建立液压电磁式脱扣器模型的基础上，对其电磁系统进行瞬态热分析，研究环境温度、通电电流与脱扣器的初始状态对其内部阻尼液黏度的影响，为在不同环境温度下脱扣器的保护特性提供了依据。

2 液压电磁式脱扣器电磁系统模型

研究对象为某型号直流设备用断路器中的液压电磁式脱扣器，其产品说明书上表明可工作在（-40～+85）℃的温度环境，额定电流9A。在PROE中对实体模型进行建模，去除支架与衔铁即为脱扣器的电磁系统，为方便分析，将线圈模型简化为空心圆柱体，如图1所示。图中：1-极靴；2-延时管（油杯）；3-线圈骨架；4-阻尼液；5-简化线圈；6-铁芯。

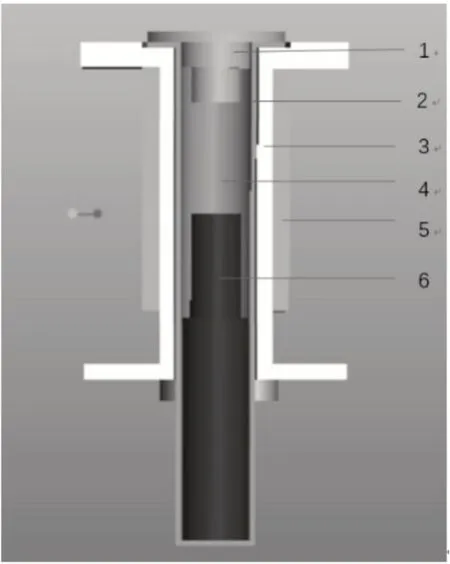
图1 液压电磁式脱扣器电磁系统模型Fig.1 Electromagnetic System Model of Hydraulic Electromagnetic Release

3 模型的生热分析与散热分析

3.1 生热分析

液压电磁式脱扣器电磁系统中其热源主要为线圈电阻的功率损耗及铁芯的涡流损耗［8］，这里研究对象为直流断路器，不考虑铁心与油杯的磁滞损耗和涡流损耗，故其热源为线圈电阻的功率损耗。

式中：D-线圈骨架外径；d-线圈导线直径；N-线圈单层匝数，线圈层数为2层，则线圈导线总长度为：

由电阻定律知：

式中：S-铜导线截面积，单位为m2；ρ-电阻率。且：

则线圈电阻为

另外铜导线的电阻率随着自身温度变化，其变化规律如下：

式中：ρ0-0℃的电阻率，ρ0=1.62×10-8Ω·m；T-线圈温度，单位为℃；a-电阻率的温度系数。所以模型发热功率为：

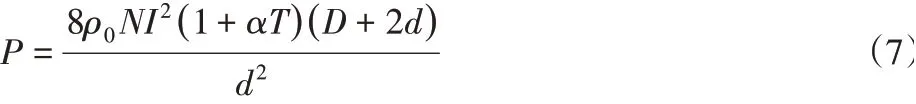
3.2 散热分析

模型的散热主要为内部的传导散热、外表面的对流散热和辐射散热。

3.2.1 内部传导散热

液压电磁式脱扣器的瞬态热传导散热方程为［10］

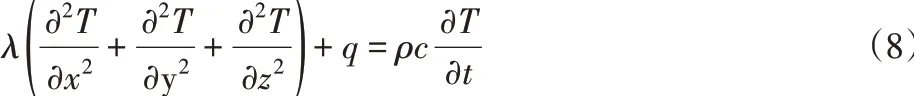
式中：l-材料的导热系数，单位为W/（m·℃）；q-单位体积内热源的生成热，单位为W/m3；ρ-材料密度，单位为kg/m3；c-材料的比热容，单位为J/（kg·℃）；t-时间，单位为s。

3.2.2 表面散热

模型的表面散热为对流散热和辐射散热，在脱扣器电磁系统所有零件外表面设置热对流系数及发射率。热对流系数由经验公式得［6］

式中：T0-环境温度，单位为℃；Tf-发热体温度，单位为℃。

3.3 载荷的添加

采用了直接耦合的方法进行热电耦合分析，将计算线圈功率损耗得出的生热率作为载荷模拟线圈的生热，考虑了功率损耗随线圈温度的变化；设置材料的热传导系数、密度及比热模拟传导散热；模型外表面设置对流散热系数与材料的发射率模拟对流散热及辐射散热，考虑了元件温度变化对散热的影响。

4 瞬态热分析

脱扣器在冷态与热态的工作状态下其元件的初始温度不同。当脱扣器处于冷态时，其各部分零件温度基本等同于环境温度。当脱扣器处于热态或半热态时，线圈生热早已作用到各部分零件并且达到稳定状态。

4.1 冷态分析

4.1.1 冷态下接入不同电流对阻尼液温度的影响

设置环境温度为25℃，模型初始温度设置与环境温度相同，仿真时间设置为1500s。当加载1倍额定电流时，模型各部分温度分布，如图2所示。

图2 环境温度25℃，加载9A电流，1500s时的温度云图Fig.2 Temperature Graph of Ambient Temperature25℃，Loading 9A Current，1500s

可以看出模型中线圈为生热体，故其温度最高，在1500s时可达到（93.877～94.305）℃。其线圈与阻尼液温度时间曲线，如图3所示。可以看出刚接入电流时脱扣器线圈与阻尼液的温度随着时间的推移近线性增高，当接入电流一段时间后其温度逐渐接近一个常数，即此时瞬态热逐渐向稳态热转变。为验证仿真的准确性，对液压电磁式脱扣器做实体实验，调节环境温度为25℃并接入1倍额定电流，实时监测1500s内线圈温度的变化并与仿真数据做对比，如图4所示。

图3 环境温度25℃，9A电流，1500s线圈与阻尼液温度时间曲线Fig.3 Coil and Damping Fluid Temperature Time Curve of Ambient Temperature25℃，Loading 9A Current，1500s

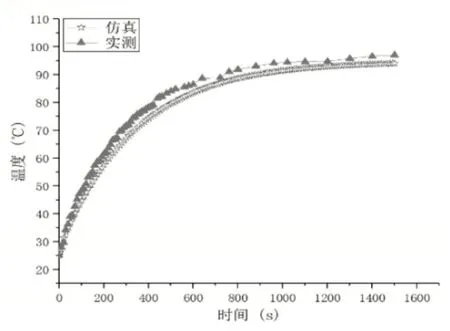
图4 环境温度25℃，9A电流，1500s内线圈温度仿真与实验对比Fig.4 Ambient Temperature 25℃，Load 9A Current，Coil Temperature Simulation and Experimental Comparison within 1500s

由图4可以看出仿真与实测数据基本吻合，1500s时，实测线圈温度为97.1℃，相对误差为3.1%。环境温度不变，当加载1.05倍与1.15倍额定电流时，其线圈温度时间曲线，如图5所示。其中实测1.15倍额定电流的线圈温度时，脱扣器将在30s内完成脱扣即开断电流，所以仿真与实测取30s内变化。

图5 环境温度25℃，线圈温度仿真与实验对比Fig.5 Ambient Temperature 25℃，Coil Temperature Simulation and Experimental Comparison

当加载1.05倍额定电流1500s时，线圈仿真温度为101.255℃，线圈实测温度为102.1℃，相对误差为0.8%。当加载1.15倍额定电流30s时，线圈仿真温度为35.811℃，线圈实测温度为36.8℃，相对误差为2.7%。接入电流时间30s，脱扣器中阻尼液在加载不同电流下的温度随时间的变化，如图6所示。

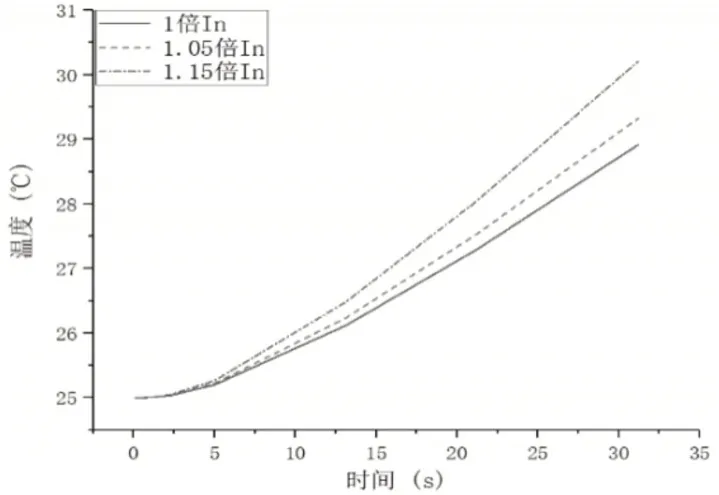
图6 环境温度25℃，加载9A、9.45A与10.35A电流，30s内的阻尼液温度变化Fig.6 Ambient Temperature 25℃，Load 9.45A and 10.35A Current，Damping Fluid Temperature Change in 30s

由上图可以看出，冷态下，当环境温度一定时，电流越大，阻尼液温度随脱扣器通电时间上升越快。

4.1.2 冷态下，环境温度对阻尼液温度的影响

实验发现，当环境温度发生变化时，液压电磁式脱扣器在初始为冷态下其动作时间有较大差异，在低温环境下会延长动作时间到，高温条件下则会缩短动作时间。故在环境温度为（-40～+85）℃范围内，对阻尼液温度进行仿真分析。设置不同的环境温度，加载1.15倍额定电流100s内其阻尼液温度变化与加载1.15倍额定电流60s时的阻尼液温度，如图7所示。由上图可以看出，环境温度越高导致阻尼液起始温度越高，且100s内阻尼液温度与时间近似成线性关系。

图7 不同环境温度下100s内阻尼液温度的变化Fig.7 Change in Temperature of Damping Fluid in 100s at Different Ambient Temperatures

4.2 热态分析

进行热态条件下脱扣器瞬态热分析时，首先要对模型进行稳态热分析，稳态分析时加载1倍额定电流，将稳态分析的温度结果作为瞬态分析的初始条件。

4.2.1 热态下接入不同电流对阻尼液温度的影响

环境温度为25℃，初始为热态的脱扣器加载1.05倍额定电流线圈与阻尼液温度时间曲线，如图8所示。

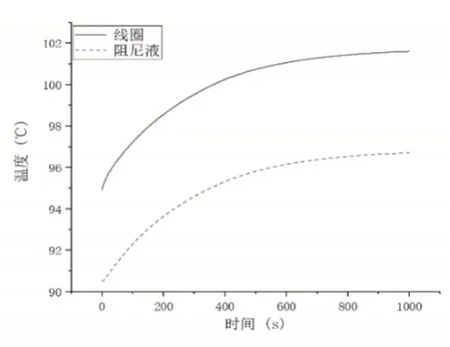
图8 加载9.45A电流，1000s内线圈与阻尼液温度时间曲线Fig.8 Coil and Damping Fluid Temperature Time Curve of Loading 9.45A Current in 1000s

由图8可以看出，初始为热态时，模型已经有一定的温度，此时改变为1.05倍额定电流导致模型温度变化相对于冷态下较小。热态下，当脱扣器加载1.05倍额定电流时线圈温度实测与仿真温度，如图9所示。

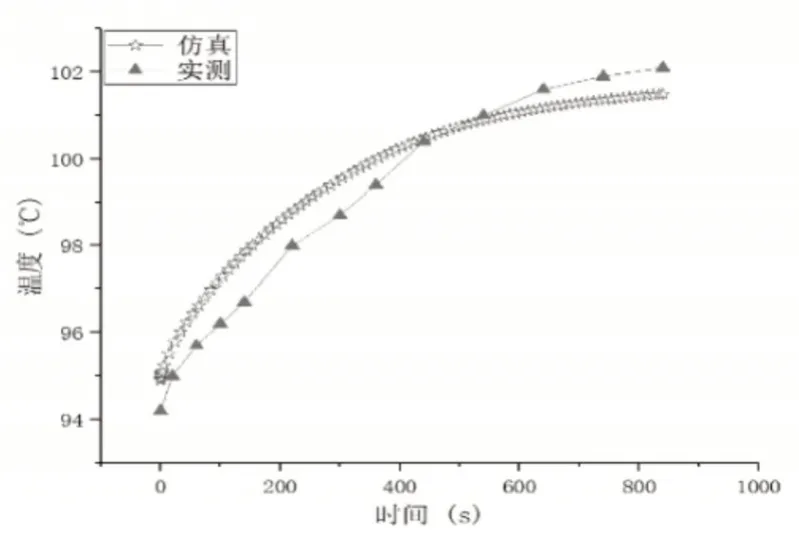
图9 环境温度25℃，840s内的线圈温度仿真与实验对比Fig.9 Ambient Temperature 25℃，Coil Temperature Simulation and Experimental Comparison within 840s

840s时，线圈温度逐渐趋于稳定，此时线圈仿真温度为101.62℃，实测线圈温度为102.1℃，相对误差仅为0.47%。环境温度25℃不变，当加载1.05倍与1.15倍额定电流时阻尼液温度在30s内变化如图10所示。热态下，当环境温度一定时，通入电流越大阻尼液温度上升越快，但阻尼液温度上升的速度较冷态下有明显的减小。

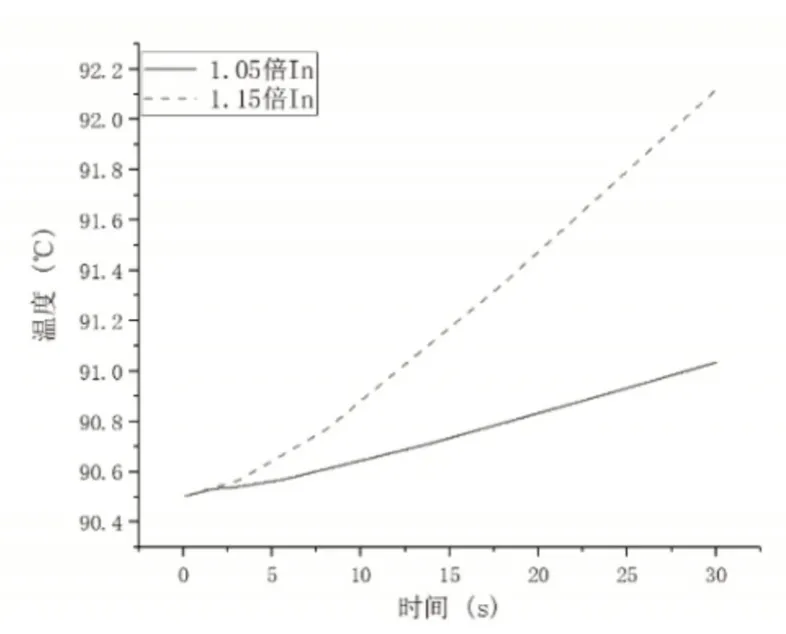
图10 30s内的阻尼液温度变化Fig.10 Damping Fluid Temperature Change in 30s

4.2.2 热态下，环境温度对阻尼液温度的影响

热态下对阻尼液温度进行仿真分析，设置不同的环境温度，加载1.15倍额定电流100s内其阻尼液温度变化，如图11所示。

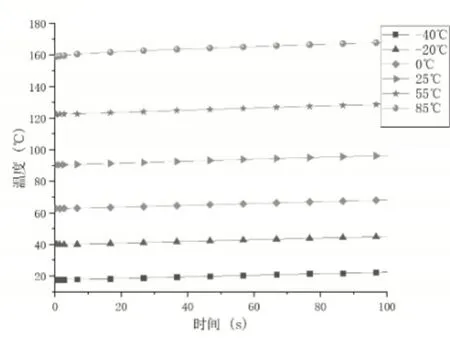
图11 不同环境温度下100s内阻尼液温度的变化Fig.11 Change in Temperature of Damping Fluid in 100s at Different Ambient Temperatures

对比图7可以看出，相对于冷态，热态下阻尼液温升不大，其主要原因为各个模型在初始状态时已经具备一定的温度，此时模型散热功率较大。

4.3 冷热态对比分析

分别取冷态与热态下，在（-40～+85）℃环境温度下通1.15倍额定电流30s时的阻尼液温度，如图12所示。

图12 冷态与热态下，阻尼液温度随环境温度的变化Fig.12 Change of Damping Fluid Temperature with Ambient Temperature in Cold and Hot State

由上图可以看出在接通1.15倍额定电流30s时，无论在冷态还是热态，环境温度对阻尼液的影响不可忽略，阻尼液温度均与环境温度近似成线性关系，且两者在图像近似相当于冷态直线向上平移得到热态直线，即在同样环境温度时，冷态下阻尼液温度要比热态下阻尼液温度低（55～65）℃。阻尼液为甲基硅油，其黏温曲线近似指数函数［11］，对该型号阻尼液进行曲线拟合，如图13所示。正是由于脱扣器在冷态下与热态下阻尼液的温差，将阻尼液黏度对温度敏感的温度范围推向了阻尼液黏度对温度相对不敏感的温度范围。所以在同样的环境条件下，热态下脱扣器的动作时间相对要稳定一些。

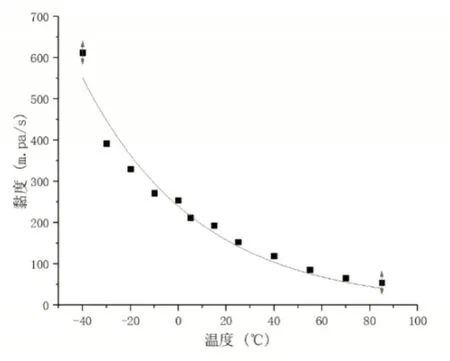
图13 阻尼液黏温曲线Fig.13 Damping Fluid Viscosity Curve

5 结论

简要说明了阻尼液温度对液压电磁式脱扣器保护特性的影响，应用ANSYS Workbench软件分别对液压电磁式脱扣器的电磁系统在冷态下与热态下进行了瞬态温度场仿真分析。仿真过程中考虑了模型生热与散热随自身温度与环境温度的变化，并与实验数据进行对比，得出结论如下：

（1）分别在冷态与热态下，将线圈仿真温度与实测温度进行了实时对比，温度时间曲线吻合较好，相对误差最大值为3.1%。

（2）环境温度与通电时间一定时，电流越大模型温度越高，且冷态下模型温升大于热态下模型温升。

（3）环境温度对液压电磁式脱扣器的影响不能忽略，冷态下环境温度对阻尼液黏度影响较大，即对脱扣器的动作时间有较大影响，而热态下环境温度对阻尼液黏度影响相对较小。