齿轮疲劳试验下的寿命估算研究

周子杰，韩振南

（太原理工大学齿轮研究所，山西 太原030024）

1 引言

齿轮箱主要由齿轮、轴、轴承和箱体构成，而因为齿轮故障失效的比例达到60%以上，如果能准确的预测齿轮的早期故障，就能够减少不必要的经济损失，所以提高齿轮接触疲劳寿命预测精度对齿轮箱的可靠性有重要的工程意义［1］。大量试验数据证明Weibull分布综合反映材料缺陷和应力集中对材料疲劳寿命的影响，因此这里结合齿轮失效机理和其载荷环境，三参数威布尔分布是齿轮最适宜的寿命分布形式［2］。

根据机床主轴寿命服从Weibull分布，文献［3］引入了Bayes理论建立了机床主轴的寿命预测模型来获得更高的可靠性；文献［4］从频率论的角度估计未知参数；文献［5］提出了钢筋C-S-N（腐蚀S-N）关系的威布尔模型，将腐蚀程度和应力范围作为威布尔模型的输入变量，采用期望最大化（EM）算法对经过审查的数据进行参数估计；将三参数Weibull分布简化为指数分布，文献［6］等简化了后验分布的求解步骤提高评估结果的精确度；滚动轴承寿命服从二参数Weibull分布特点，文献［7］利用小样本数据将无信息先验分布作为其先验分布，给出了形状参数与可靠度的点估计并编写了计算机程序；文献［8］等运用平均秩次法为经验分布函数获取误差大的问题提出合理的方法；文献［9］等将降阶的思想与二分法结合，为三参数weibull分布的极大似然估计值提供了新思想。

文献［10-11］只提出了三参数Weibull分布的参数估计方法以及模型的建立，仅仅利用蒙特卡罗仿真方法产生样本数据，并没有详实的实验数据，缺乏可靠性。而且国内外以齿轮为研究对象的寿命预测方法研究很少，多数局限于有限元仿真和计算机程序的编写，难以为实际生产提供工程意义。基于上述研究，结合齿轮疲劳试验，提出利用最小二乘法进行参数估计和近似中位秩公式对经验分布函数进行拟合，通过绘制故障概率密度函数和可靠度函数准确的得出齿轮接触疲劳寿命预测值，通过详尽的实验数据得出齿轮早期故障期的可靠度规律。

2 Weibull分布理论基础

失效分布函数为：

故障密度函数为：

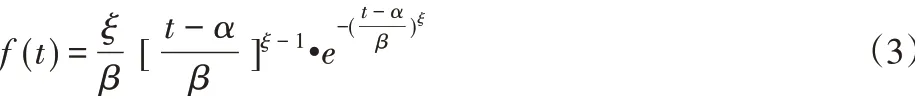
故障率函数为：

式中：t-试验齿轮在规定扭矩下的循环次数；β-尺度参数，对应于齿轮副的特征寿命；位置参数α，描述齿轮副最少的无故障循环次数；形状参数ξ，它的值不同，随机变量的分布也不同，其中β＞0，ξ＞0。

3 参数估计

最小二乘法的法则是通过最小化误差的平方寻找数据的最佳函数匹配，运用此法可以使齿轮的寿命预测值更准确。在齿轮副实际工作中，对寿命影响大小而言，α值的影响可以被忽略不计，因此令α=0，则式（1）等价成二参数Weibull分布的可靠度函数：

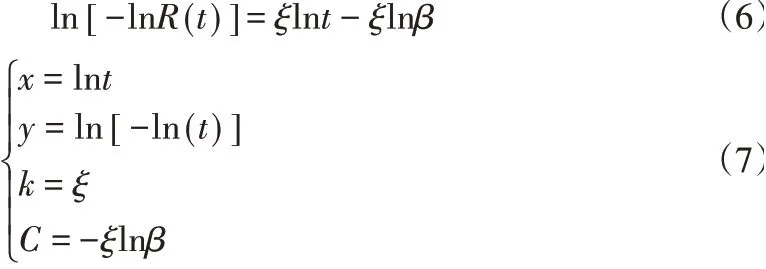
两边各自取两次自然对数变换，并整理得

则式（6）简化为：

目前，我国存贷款利率水平主要由政府决定，并非市场供求因素形成，行政体制保护下的管制利率成为银行能够获得超高收入和利润的最大保障。近几年，由于整个社会资金面相对紧张，相对借款人而言，商业银行议价能力不断提升，从而导致利差水平上升，平均上升幅度在0.3%左右[5]。所以，利息收入的增长依然是我国商业银行利润走高的主要支撑因素。

由线性回归方程（8）得出，回归系数k和C的最小二乘估计解经最小二乘法法则变换为

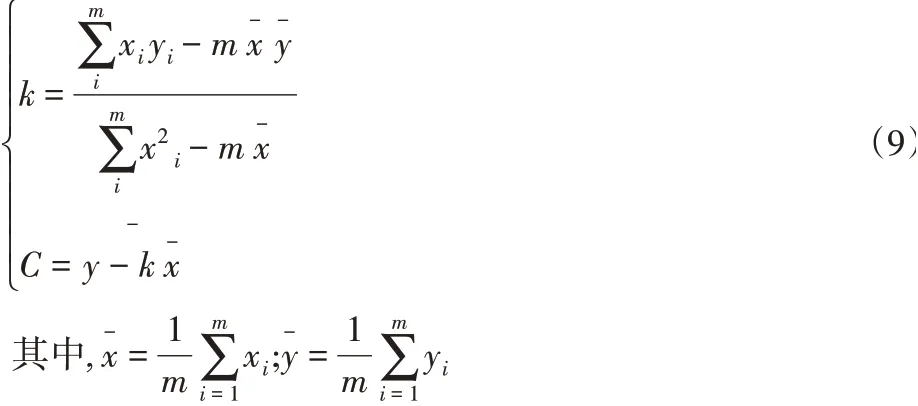
在使用最小二乘法对Weibull分布进行参数估计时，要想使回归直线拟合精度更高，得到的回归系数估计值更加符合实际经验分布函数的精度的提高是根本要求。

经验分布函数在齿轮可靠性应用中举足轻重，当样本量很大时，由一个样本值得到的经验分布函数Fn(t)是总体分布函数F(t)的优良估计。经查阅资料可得近似中位秩公式在实验设备全部故障的情况下误差较小，由于在齿轮疲劳试验中我们得到的是设备全部故障的数据，所以完全适用于该计算方法。

式中：i-齿轮副的载荷谱编号；n-载荷谱总数。

4 齿轮接触疲劳试验

4.1 试验齿轮

考虑试验机的条件，选取的试验齿轮是渐开线直齿圆柱齿轮，齿轮传动比为1：1，齿轮参数，如表1所示。

表1 试验齿轮参数Tab.1 Parameter of Test Gear

4.2 疲劳寿命实验条件

（1）试验在如图1所示的台架上进行。

图1 机械式功率流封闭齿轮试验台Fig.1 FZG Gear Test Rig

（2）试验电机转速为1200r/min。

（3）加载方式为杠杆加载，八级载荷谱。

（4）试验齿轮安装方式选用错齿安装，使得相同输入扭矩下得到更大的齿面接触应力，啮合齿宽为10mm。

（5）润滑条件。L-CKC320工业闭式齿轮油，粘度等级：320，40℃，运动粘度：324（cst）闪点：224（℃）。

（6）试验时间。每三十分钟记录一次数据，每一个小时检查一次齿面，记录齿面磨损情况和润滑油面高度，同时观察仪表监测数据，直到出现点蚀疲劳现象为止。

4.3 接触疲劳失效判据

点蚀通常出现在节线的齿根部分，呈痘状或条状。当试验齿轮单齿点蚀面积率达4%或者齿轮副点蚀面积率达0.5%时，认为该组齿轮试验失效［13］，对应的循环次数即为该应力水平下的齿轮疲劳失效寿命。

4.4 试验应力水平的确定

每一级载荷所对应的齿轮接触应力依据以下公式［14］进行计算：

式中：u-两齿轮的齿数比，u=z2/z1；弹性系数ZE=189.8；齿轮的重合度为1.45；重合度系数Zε=0.92；节点区域系数ZH=2.12；使用系数KA=1.5；动载系数KV=1.2；齿间载荷分配系 数KHα=1/(Zε2)；齿 向 载 荷 分 配 系 数KHβ=1.2；K=

对（11）进行简化得：

式中：b-啮合齿宽（mm）;T-转矩（N·m）。

5 实验数据及处理结果

5.1 实验数据

通过NC-3扭矩测量仪记录疲劳试验的转速转矩功率和时间（注：第八级载荷的循环次数为出现点蚀疲劳的循环次数），数据如表2所示。

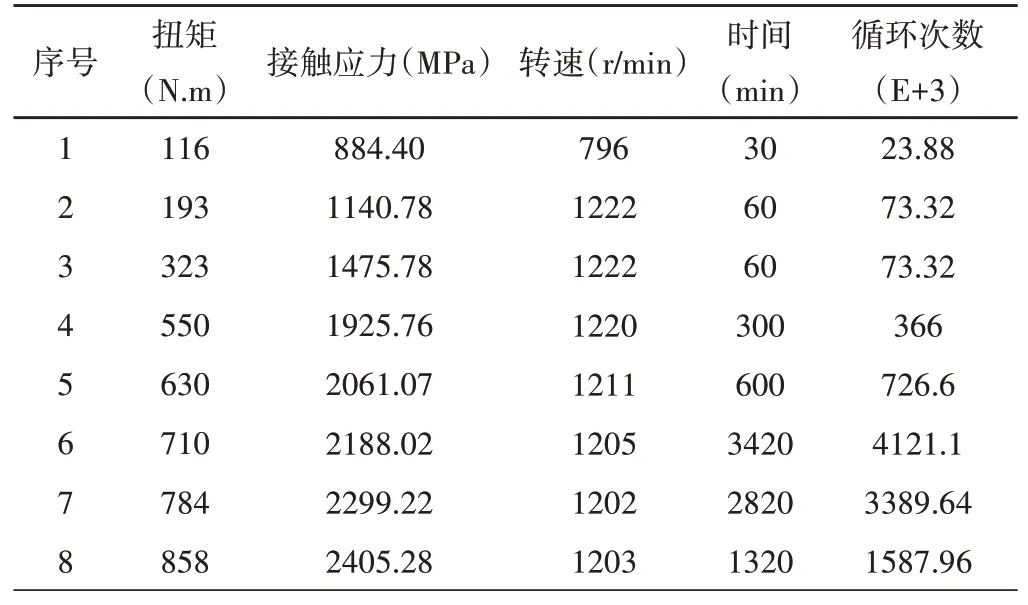
表2 实验扭矩与齿轮转数Tab.2 Experimental Torque and Gear Revolution

5.2 试验数据处理

对表2中的故障数据利用式（7），式（10）分别计算得到齿轮的经验分布函数，如表3所示。

表3 经验分布函数Tab.3 The Empirical Distribution Function

通过式（9）可知，x和y成一次函数关系，利用origin软件对表中数据直线拟合后，结果如图2所示。从拟合图中可以直观地看出数据均匀的分布在拟合直线上以及两侧，对经验分布函数利用近似中位秩公式的拟合效果和精度都可以满足要求。

图2 直线拟合Fig.2 Linear Fitting

5.3 齿轮寿命预测分析

利用近似中位秩公式计算分析，得出直线回归系数最小二乘解为：k=0.5265，C=-7.3209。将其代入式（7）得到k=ξ=0.5265，β=e-c/ξ=1105933.132。利用式（5）并根据齿轮副寿命的可靠度函数、失效分布函数以及故障概率密度函数三者关系，将k和β的值代入可以得出可靠度函数、失效分布函数以及故障概率密度函数方程：

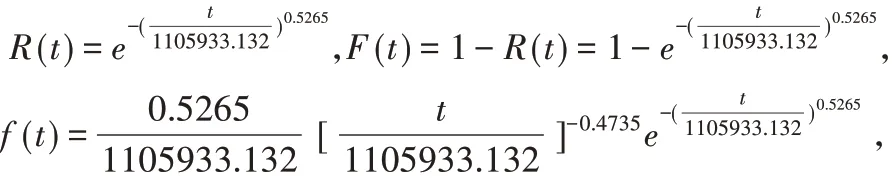
已知方程，利用Matlab8.0软件分别得到如图3所示的Weibull分布故障概率密度曲线，如图4所示的失效概率曲线和如图5所示的可靠度曲线。

图4 失效概率函数曲线Fig.4 The Curve of Failure Rate Function

由图3可知，故障概率密度函数曲线与形状参数ξ紧密相关，当ξ=0.5265＜1，概率密度曲线在低循环次数下迅速下降，随着循环次数增加逐渐趋于平缓，没有峰谷值，这一现象表面齿轮点蚀现象出现在齿轮机构的早期故障期，齿轮机构并没有完全失去工作能力，但是需要定期检查齿面状况，及时调整齿轮机构的工作载荷，防止出现最严重而且危害很大的断齿现象。

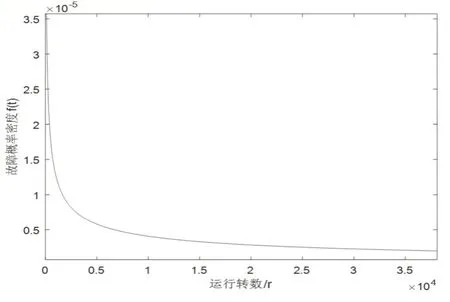
图3 故障概率密度函数曲线Fig.3 The Curve of Failure Rate Density function

由图5可得，可靠度函数曲线也与形状参数ξ紧密相关，试验中齿轮的形状参数ξ=0.5625＜1，可靠度函数曲线在低循环次数下迅速下降，随着循环次数增加逐渐趋于平缓，这是由于齿轮的早期疲劳点蚀失效率较高造成的结果，当可靠度为R（t）=50%时，代入可靠度函数，得出循环次数t50%=0.55×106r，表明在该实验工况下，齿轮的循环次数达到0.55×106r后，可靠性下降到50%，需要停机观察齿轮表面的点蚀坑的面积来判断齿轮机构是否可以继续运行。

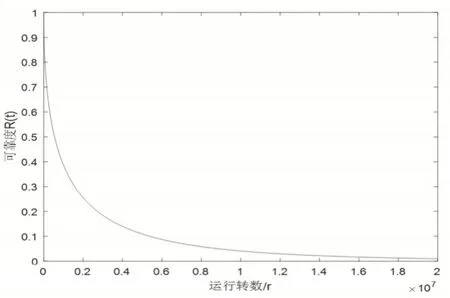
图5 可靠度函数曲线Fig.5 The Curve of Reliability Function

6 结论

简要的阐述了三参数weibull分布的理论基础，利用最小二乘法进行参数估计的方法和近似中位秩公式的表达，结合机械封闭流齿轮实验台架的接触疲劳试验，利用实验数据进行分析，应用origin软件进行近似中位秩公式的拟合，直线拟合的效果和精度令人满意。利用Matlab准确的拟合了试验齿轮的故障概率密度函数曲线，可靠度函数曲线和失效概率函数曲线，结果表明，齿轮的疲劳点蚀现象出现在早期故障期，并且点蚀失效率较高，当齿轮的循环次数达到0.55×106r，可靠度下降到50%，需要停机观察齿轮表面的点蚀坑的面积来判断齿轮机构是否可以继续运行。为有效的解决旋转部件寿命预测提供了新的思路。