深厚软土基坑地下连续墙支护优化设计及其评价
蔡子勇,汤建铭,唐建桥,卞元靖,乔世范,历彦军
(1. 中南大学 土木工程学院,湖南 长沙 410075;2. 中铁广州工程局集团有限公司,广东 广州 511457;3. 中国铁路广州局集团有限公司,广东 广州 510088)
基坑工程作为临时工程项目是一个极具挑战性、高风险性、高难度的岩土工程热点课题,基坑支护结构设计的合理与否对施工安全风险影响极大[1−3],支护设计的优劣直接关系着基坑开挖及支护结构的安全与经济。因此,在满足基坑安全稳定的前提下,寻求最佳支护设计参数,使工程造价最低,一直是工程所面临的一大难点问题。关于基坑支护优化问题,国内外学者对此进行了大量研究。早在20 世纪60 年代,周瑞忠等[4−6]提出遗传优化算法,在基坑支护优化设计方面得到广泛应用。由于支护型式各异,各设计参数之间敏感性不同,存在非线性函数优化迭代时局部不收敛或收敛速度较慢的问题,于是有学者提出新的优化理论及改进算法,成功的应用在桩锚支护[7−8]、土钉支护[9−10]及灌注桩+锚杆支护[11]的基坑优化设计中,取得较好的优化效果,还有学者通过MAT‐LAB 编程实现更快的优化迭代运算能力,在很大程度上为基坑优化设计提供便利[12−13]。后来,随着计算机技术快速发展,各大型商业软件成为基坑支护优化设计常用的一种研究手段[14−17],由于限制条件少,可分析变量因素多,受到人们的青睐。汪俊杰等[18]基于FLAC3D软件对地连墙厚度、地连墙深度、支撑刚度及预加轴力进行参数敏感性分析,确定最优参数组合。陶勇等[19]采用PLAXIS 软件,从支撑刚度、支撑位置及支撑预加轴力3个方面对地下连续墙内支撑结构进行优化分析。程池浩等[20]采用PLAXIS 软件从地连墙插入比、地连墙厚度、支撑道数及土体加固深度4个方面对基坑围护结构进行优化设计,得到最优支护设计参数取值。为了验证数值模拟理论优化结果的合理可靠性,BAI等[21—23]结合现场监测数据对基坑数值模拟优化结果进行评价,验证了其可行性,为类似工程应用提供较好的参考依据。鉴于此,前人虽对基坑支护结构优化设计作了大量相关研究,但更多的存在研究方法单一,缺乏理论优化比较及工程实践验证,而且对于沿海深厚软土窄长深基坑地连墙支护优化研究较少。相关研究表明,窄基坑较其他类型基坑支护结构变形要小且具有更好的稳定性[24],由于目前规范建议的基坑设计方法未考虑基坑宽度的影响,导致窄基坑的设计偏保守。因此,本文以广州南沙港铁路隧道深基坑工程为例,采用遗传算法从地连墙厚度、墙体嵌入深度及支撑位置3个方面对地下连续墙支护结构进行优化设计,确定最佳的设计参数,结合ANSYS 软件对优化前后进行比较分析,通过现场监测结果进行可行性验证,对指导软土地区深基坑施工具有重要的工程意义。
1 地连墙设计方案
以新建广州南沙港铁路隧道深基坑工程为背景,隧道起止里程为NBDK0+500~NBDK7+020,其中敞开段2 020 m,暗埋段4 500 m,采用明挖法施工,基坑开挖深度0~14.9 m,基坑宽度约7~9 m。隧道周边环境复杂,地质条件差,场地分布有淤泥(淤泥质土)等松散软弱土层,呈流塑~软塑状,平均层厚15.94 m,整个隧道底板处于软土层中,且地下水位较高,珠江水直接与地下水相通,透(含)水性强,局部含承压水。基坑的安全等级:H≤5 m,为3 级;H≥10 m,为1 级;其余为2 级。综合考虑工程地质条件差、对基坑变形及周边环境要求高、施工风险大等特点,对于1级基坑施工区域(H≥10 m),围护结构采用地下连续墙+内支撑支护方式,该方案一致得到评审专家的认可。本文选取NBDK4+370 断面地连墙支护结构进行优化设计,该断面采用800 mm厚地下连续墙+第1道钢筋混凝土支撑+3 道φ609 钢管支撑体系,基坑开挖深度13.96 m,开挖宽度为8.3 m,地连墙插入比为1.5,地面超载取20 kN/m2,地下水距地面1.9 m,地面标高4.2 m,各土层参数指标见表1 所示,地连墙支护结构断面如图1所示,基坑施工照片如图2所示。
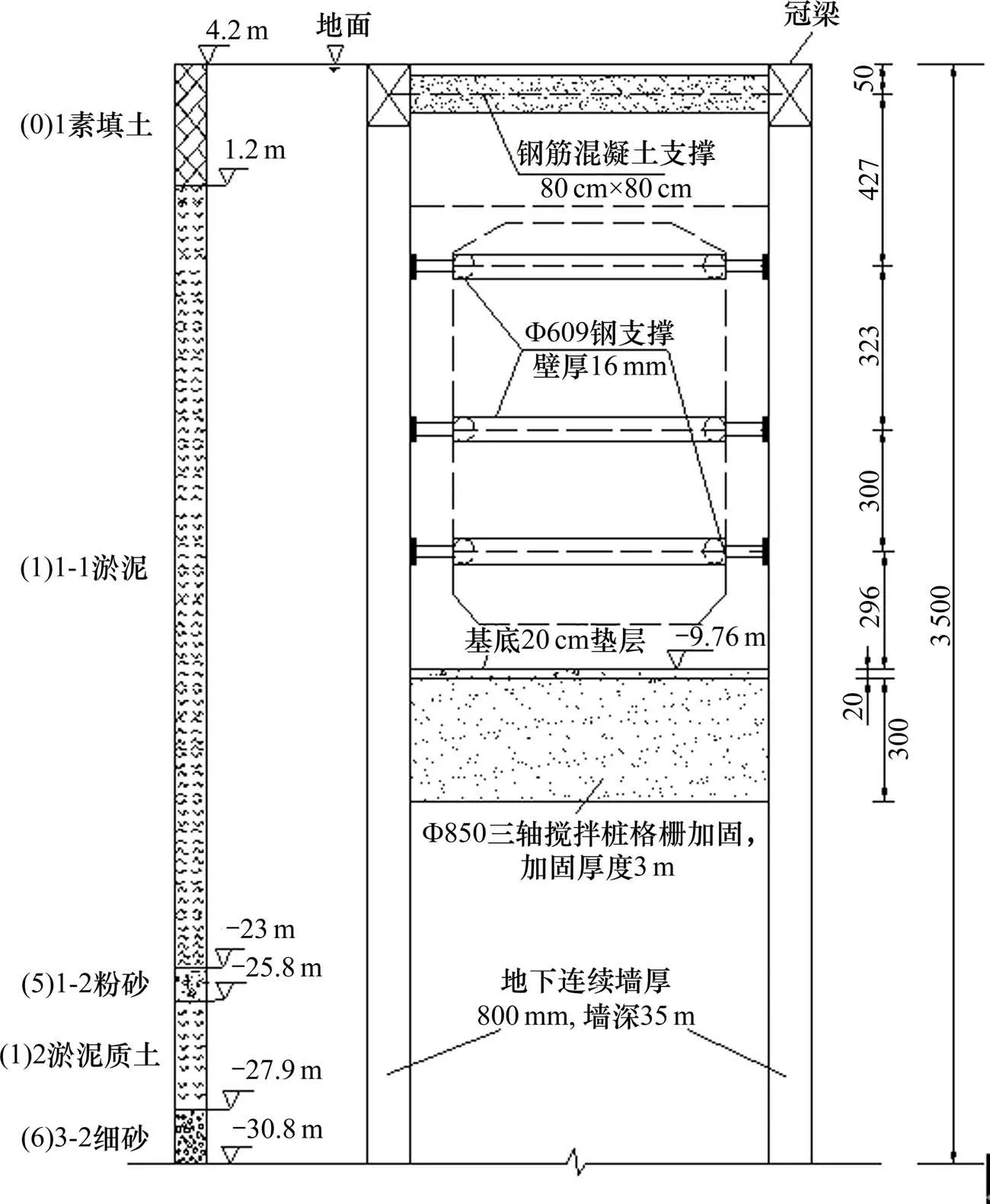
图1 地连墙剖面Fig.1 Section of diaphragm wall

图2 基坑施工照片Fig.2 Photo of foundation pit construction

表1 NBDK4+370断面土层物理力学参数Table 1 Physical and mechanical parameters of soil layer at NBDK4+370 section
2 建立地连墙优化模型
2.1 设计变量选取
设计变量反映了优化设计的内容,合理地选取设计变量是结构优化设计的前提。根据文献[25]对地下连续墙优化设计变量的敏感性分析,认为地连墙的厚度、墙体嵌入深度和支撑位置对地连墙的设计十分重要。因此,本文选取设计变量:

式中:x1,x2,x3分别代表地连墙的厚度、墙体嵌入深度和支撑位置。
2.2 目标函数的确定
地连墙支护结构的工程造价一般包括墙体、内支撑和施工费用等,为简化目标函数,不考虑施工费用,内支撑由于可以回收利用,忽略其造价影响。因此,将单位长度地连墙的工程造价作为目标函数,在满足约束条件的前提下取最小值,即为总造价最低的优化结果。则:
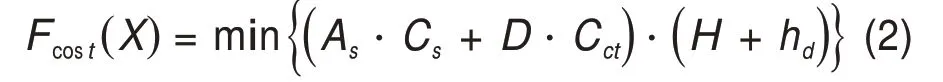
式中:As为地连墙所配受力钢筋的横截面积;Cs为单位体积钢筋的造价;D为地连墙的厚度;Cct为单位体积混凝土的造价;H为基坑开挖深度;hd为墙体的嵌入深度。
2.3 约束条件
1) 设计变量约束
地连墙厚度D:0.6 m,0.8 m,1.0 m,1.2 m;嵌固深度:hd∈[0.2H,0.6H];
支撑道数:2道支撑,3道支撑,4道支撑;
支撑位置:第1 支撑点:设置在地连墙顶部,采用0.8 m×0.8 m 的钢筋混凝土支撑,第2 支撑点ha:3 ≤ha< 5,第3 支撑点hb:ha+ 3 ≤hb 2) 设计准则约束 ①强度约束 地连墙墙体必须满足一定的强度要求,保证其不发生破坏,根据设计弯矩进行配筋,得到强度约束的表达式为: 式中:Ms为设计弯矩值;γ0为结构重要性系数;γF为作用分项系数;M为最大计算弯矩值。 ②整体稳定性约束 对于地下连续墙,需要保证其整体稳定性,嵌固深度采用整体稳定性条件进行约束,基坑安全等级为1级,其公式为: 式中:cj,ϕj为第j个土条在滑弧面上的黏聚力、内摩擦角;lj为第j个土条滑弧段的长度;qj为作用在第j个土条上附加分布荷载的标准值;bj为第j个土条的宽度;θj为第j个土条滑弧面中点的法线与垂直面的夹角;ΔGj为第j个土条的自重。 ③变形约束 地下连续墙支护结构最大水平位移应符合下式要求: 式中:δ为墙体的最大水平位移;[δ]为墙体允许变形量,根据《建筑基坑工程监测技术规范》(GB50497―2009),当基坑安全等级为1 级,取[δ]=50 mm。 在满足约束条件gj(X)≥0 的条件下,求最优设 计 变 量X满 足Fcost(X) →min, 其 中X={x1,x2,x3},F值越小,表明可行解的性能越好。支护结构内力与变形按《建筑基坑支护技术规程》(JGJ—2012)[26]中弹性支点法进行计算。 使用MATLAB 遗传算法工具箱对基坑支护结构进行优化,计算结果见图3~4所示。 图3 最佳适应度和平均适应度Fig.3 Best and average fitness 图4 优化参数取值Fig.4 Optimization parameter value 优化的最终结果为:第2 层支撑位置4.17 m,第3 层支撑位置7.59 m,第4 层支撑位置10.8 m,地下连续墙的嵌入深度为18.64 m,地连墙厚度仍然为0.8 m,具体见表2。 表2 优化结果对比Table 2 Comparison of optimization results 可以发现,通过采用遗传算法对支撑位置、墙体嵌入深度以及地连墙宽度进行优化调整,节省工程造价12.7%,减小了墙体的配筋,在满足基坑安全的前提下,达到了降低成本的目的,说明遗传算法的优化结果是可行的。 以NBDK4+370 断面为例,通过ANSYS 软件建立基坑开挖模型,选取墙外侧20 m 土体作为有效土体,定为X轴方向,选取嵌入深度以下15 m作为影响深度,定为Z轴方向,纵向取12 m 长度,定为Y轴方向。地连墙与各道支撑均采用线弹性模型,土体采用D-P准则。边界条件:土体侧表面约束法向位移,土体底部约束竖向位移,土体顶面为自由边界。基坑开挖模型如图5所示。 图5 基坑开挖计算模型Fig.5 Calculation model of foundation pit excavation 根据开挖步骤及支护情况分为5个工况,具体见表3。 表3 基坑施工工况Table 3 Construction condition of foundation pit 建立基坑开挖模型,模拟不同工况下基坑地下连续墙墙体水平位移与开挖深度关系曲线见图6。 图6 不同工况下墙体水平位移与深度的关系Fig.6 Relationship between horizontal displacement and depth of soil under different working conditions 可以看出:1) 优化前后墙体水平位移变化趋势基本一致,呈先增大后变小的趋势,整体呈“勺”状;2)优化后的水平位移变化相比优化前位移有所改善,优化结果可行,从优化参数角度分析,在一定嵌入深度范围内,随着嵌入深度的增加,对变形控制影响并不明显;3) 基坑最大水平位移位于开挖底面附近,墙体主要影响深度约为基坑开挖深度的2倍。 在NBDK4+370 断面地连墙墙体内埋设测斜管,监测墙体深部水平位移,通过对土体开挖过程现场监测数据进行分析,得出基坑开挖过程墙体深层水平位移变化曲线如图7所示。 图7 基坑开挖墙体深部位移Fig.7 Deep displacement of soil behind excavation wall of foundation pit 可以看出:1) 基坑开挖过程墙体深部水平位移变化曲线呈现“两头小、中间大”。2)随着基坑开挖深度的增加,墙体深部水平位移经历“先缓慢增长-再快速增加-最后趋向稳定”过程,在顶部与底部位移变化较小,开挖至基坑底面,水平位移最大值为25.05 mm,处于容许变形范围;3) 墙体深部水平位移最大位置位于基坑开挖底面附近,结构主要影响深度大约为基坑开挖深度的2倍,进一步验证了优化结果可行。 1)基于沿海地区深厚软土基坑围护结构特点,建立以地连墙厚度、墙体嵌入深度及支撑位置为变量设计参数,以工程造价最低为目标函数的地连墙数学优化模型。 2) 采用遗传算法对地下连续墙支护结构进行优化设计,在确保基坑安全的前提下,不仅可节约成本12.7%,而且还能够缩短工期,既安全又经济。 3)通过有限元ANSYS 软件对支护结构优化前后分析比对,验证了遗传算法的优化可行性,优化后的位移变化相比原设计有所改善,从优化参数角度分析,在一定的基坑开挖深度下,随着墙体嵌入深度的增加,对变形控制影响并不明显。 4) 考虑基坑周边堆载、运土车辆荷载及降雨等影响,从实际情况来看,现场监测结果相比数值模拟结果稍偏大,但整体变化规律基本一致,深层最大水平位移位于基坑开挖底面附近,主要影响深度约为基坑开挖深度的2倍,为实际工程建设提供了参考依据,具有一定的工程应用价值。


2.4 优化算法
2.5 优化结果
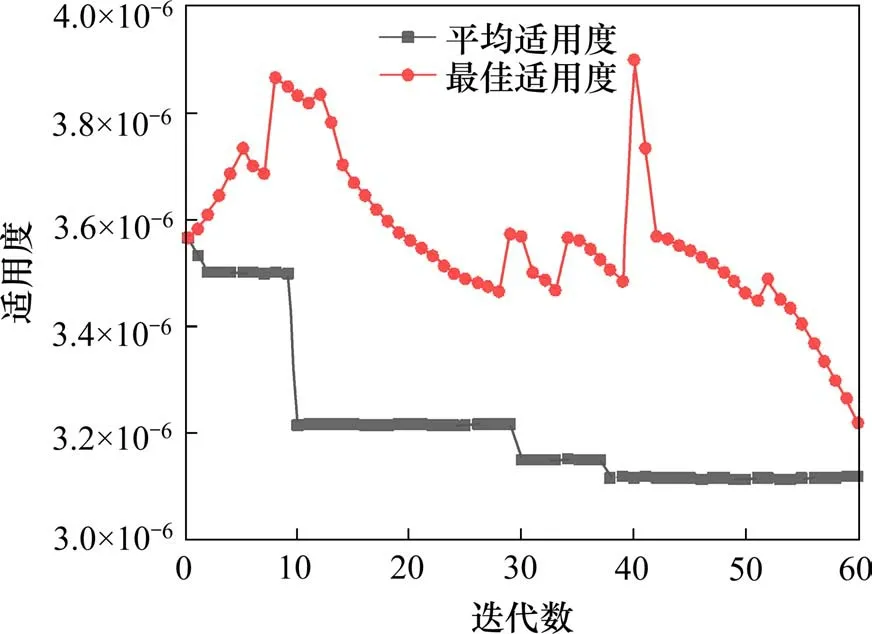

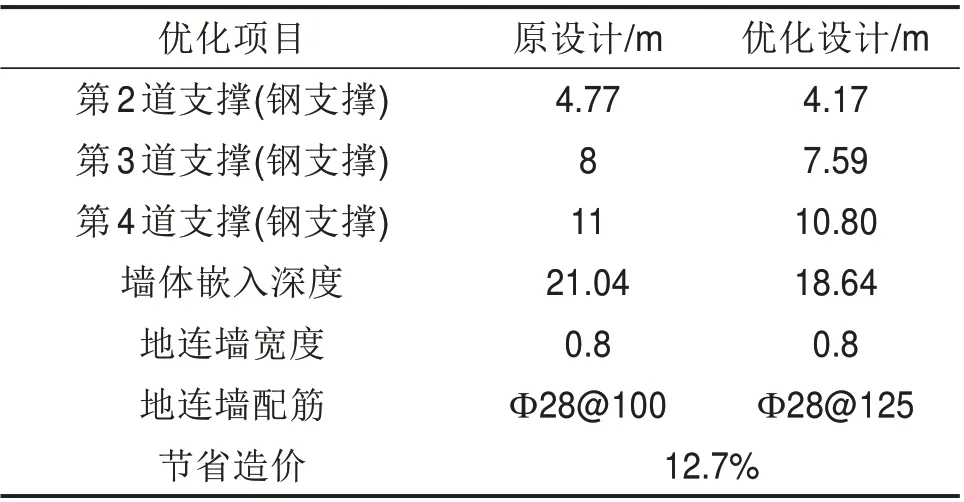
3 优化前后数值分析比较
3.1 模型建立
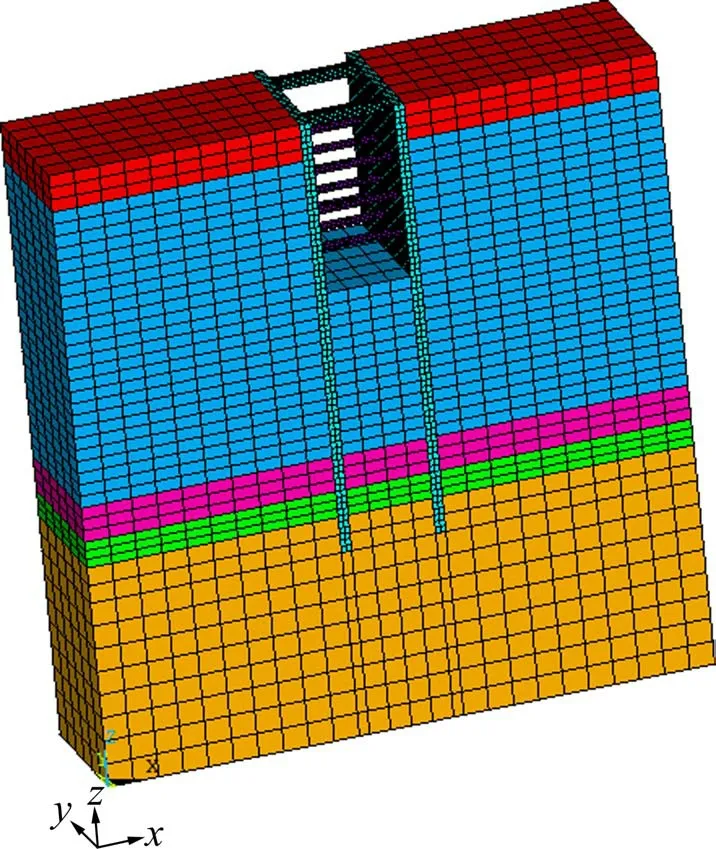
3.2 工况模拟

3.3 不同工况模拟结果分析

4 现场监测结果分析
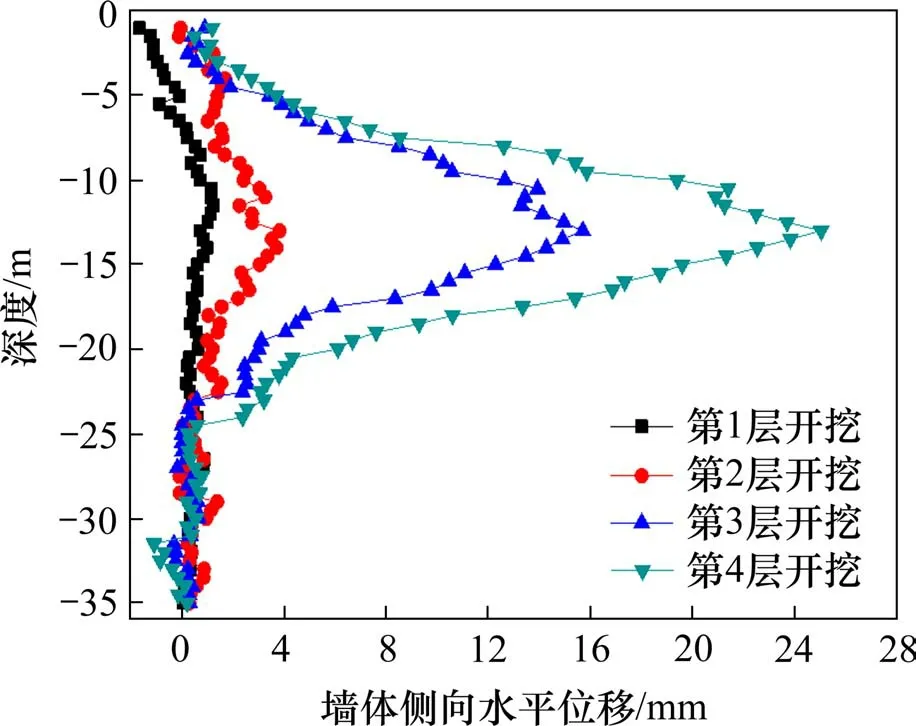
5 结论

