基于模块服役状态的盒式连接可重构型架稳定性评估方法
张宏博,郑联语,王艺玮
北京航空航天大学 机械工程及自动化学院,北京 100083
航空制造业中,飞机装配是整个飞机制造过程的核心,其工作量占总工作量的50%~60%。装配型架作为一种重要的生产工艺装备,在保证飞机装配质量、提高劳动生产率、减轻工人劳动强度等方面具有重要作用。尤其在保证飞机产品质量方面,装配型架的稳定性是影响飞机部件几何尺寸、互换协调及气动外形等重要因素之一。
目前,国内外航空工业界及学术界对飞机装配型架的稳定性尚未有统一定义。杨亚文和李策[1]认为型架的稳定性是指在型架上安装的各类产品质量的一致性。该定义是从飞机产品装配质量层面表征型架的稳定性,其评估方法所得结果具有滞后性,不能真实反映型架当前的服役状态,易造成产品装配的不合格。Martin等[2]认为型架的稳定性是指其在长期服役阶段保持自身精度的能力,该能力可通过对型架服役状态长期、定时的监测进行评估,即目前航空工业中采用的定检评估方法。但是该定检过程费时、费力且某一时刻的服役状态指标并不能准确的反映型架长期服役的能力。因此该方法可能导致出现两种情况:① 定检过剩,即装配型架满足作业要求时定检;② 定检不足,即装配型架不满足作业要求时未定检。前者虽然保证了装配任务对象的质量,但频繁的定检导致生产制造成本提高;后者不仅造成了昂贵的产品返修成本,而且也滞后了工作进度。
近年来由于传统焊接装配型架在面对飞机机型多样且样机制造阶段频繁改型的情况时,所暴露出诸如生产准备周期长、制造成本高以及型架存放占用空间大等问题制约了航空制造业的发展[3]。盒式连接可重构装配型架作为一种新颖的可重构工装具有重用性、集成性、转换性和模块性等特征,为解决传统焊接型架所造成的困境提供了有效途径[4],但其稳定性相对传统焊接型架存在不足,传统的型架稳定性评估方法无法满足对盒式连接可重构型架稳定性的判断。作者认为,可重构型架的稳定性评估需要从型架设计、制造和使用等全生命周期进行综合研究,涉及测量和监控、结构和材料、安装规范、使用环境等多个方面,同时需要引入现代产品服务中健康服役的理念和方法。
型架检测方面,英国巴斯大学创新设计制造研究中心联合空客公司提出一种测量辅助工装应用(Metrology Enhanced Tooling for Aerospace, META)技术框架,即采用多种测量设备分别实现大尺寸整体测量和局部测量,测量结果通过采集、计算、分析,实时或准实时的反馈给工人、专家,实现对型架服役状态的实时监测[2,5],但未见后续深入研究和报道。照相测量可以用于型架的稳定性分析和定检,如美国的GSI公司与诺斯罗普·格鲁曼合作,利用V-STARS系统对波音-777襟翼型架的关键特征进行照相测量,结果表明V-STARS系统能够显著地提高测量速度[6],但照相测量结果受被测目标和现场环境限制。林雪平大学和空客公司合作研究指出,由于可重构装配型架服役周期内受力情况复杂,导致无法用理论计算获取准确的变形结果,因而针对其稳定性开展了关键点位置精度的监测实验研究[7]。该实验过程仅针对无装配任务且处于静置状态下的型架进行长时间监测,其监测结果无法反映型架在使用阶段时的服役状态。
型架结构设计方面,刘忠良[8]提出设计合理的型架结构是解决型架骨架刚度和保证型架关键定位点位置精度的有效措施,并给出了具体的工程实践指导;潘志毅等[9]针对型架结构布局设计提出了人机域优化求解方法,考虑了人因工程对型架稳定性的影响;洪学玲等[10]和黄海军[11]分别针对型架骨架刚度进行了有限元分析,并根据分析结果开展骨架总体尺寸和型架梁截面尺寸的优化设计,提高了型架的稳定性;刘清军[12]提出基于稳定性的型架优化设计方法,通过构建饱和型架模型,实现了以型架稳定性为目标的结构拓扑优化设计。
型架使用环境方面,刘忠良[13]指出热膨胀系数的不同导致温度变化引起的地面垂直变形的不均匀,以及型架材料热胀冷缩的不一致,是产生型架关键定位点漂移的主要原因,并给出了不同结构形式、不同材料型架的热膨胀综合误差计算公式;杨亚文和李策[1]更进一步提出了消除温度影响型架稳定性的方法。
型架作为一种特殊的工艺装备,其服役健康状态监测与评估可以借鉴装备健康管理的研究成果。许多学者对机械装备的健康状态评估进行了研究,即依靠先进的状态监测手段、可靠的评价方法和完整的运行数据来评判当前的健康状况[14-15]。此类方法主要依靠多种类型传感器进行数据采集,但通过对多家航空企业现场调研,发现上述研究不适用于可重构装配型架的服役状态评估,主要原因是:
1) 型架服役期内飞机产品装配多以手工作业为主,且型架上关键测点数量众多,如果采用大量传感器进行实时监测,将导致成本急剧增高且监测系统的引入使得装配现场不利于工人操作,延长生产周期。
2) 传统评估方法通常是建立在大样本基础上,然而对于航空工业,样本本身造价昂贵,同时对多个样本进行试验监控的做法也不现实。
3) 型架失效(定位点漂移超出阈值)过程一般属于性能退化的过程,当前评价指标采用某一时刻测点坐标值与理论值对比,以是否超出阈值的二分法作为型架性能的评判标准,该指标无法表征型架在某一时间段内服役状态的退化情况,不利于失效状态的预测。
因此,首先针对盒式连接可重构型架(以下简称型架)服役过程进行详细分析,指出该过程是由作业期和空置期交替组合而成,并给出型架服役稳定性及表征其优劣的服役稳定度定义。依据定义,考虑盒式连接可重构型架模块化特征及作业期与空置期的不同情况,提出融合测量数据和多源稳定性影响因素分析的盒式连接可重构型架稳定性评估方法,最后以某型垂尾盒式连接可重构装配型架为实验对象,以验证方法的有效性。
1 盒式连接可重构型架服役过程分析
型架服役期是指型架从准备期(Preparatory Period)结束到型架上关键测量点漂移失效为止,交替经历了作业期(Operational Period)和空置期(Idle Period)。作业期,即型架处于装配任务执行阶段,期间由装配过程产生的不确定影响因素众多,难以甚至无法使用激光跟踪仪或传感器进行长时间监测;空置期,即型架处于装配任务的间歇阶段,此阶段可采用激光跟踪仪进行测量作业。若测量结果表征为失效,则服役期结束;反之,则进入下一个作业期。如图1所示,与传统焊接型架不同,盒式连接可重构装配型架服役期结束后返回准备期,通过检修或更换失效模块的方式使得型架重新进入新一轮的服役周期。
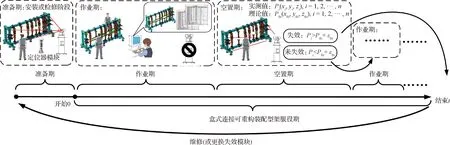
图1 盒式连接可重构装配型架服役期Fig.1 Service period of box-joint reconfigurable assembly jig
由上述分析可知,型架服役期内不同阶段的服役状态受装配任务执行情况的影响而存在波动变化,尤其作业期内型架服役状态变化的程度将直接影响产品的装配质量。空置期虽然可以获取某时刻关键点测量信息,实现空置期服役状态评估,但并不能准确反映型架长期服役的能力,仅可视为型架能否进入下一轮作业期的预检验,即作业期初始服役状态检验,而该状态的不同在一定程度上也影响了型架的服役能力。因此,首先给出了型架服役稳定性及表征其优劣的服役稳定度定义:
定义1服役稳定性是指描述型架保持自身精度以执行装配任务的能力。在某种程度上,服役稳定性反映了型架在服役阶段的一定时间内,其服役状态保持在一定范围的能力。
定义2服役稳定度是表征服役稳定性优劣的度量,记为W。指从某一时刻型架处于某一服役状态开始,在一定时间内其服役状态保持在一定范围内的概率,稳定度越高,则稳定性越好。
根据定义,从服役状态退化的角度提出基于型架关键测量特性的空置期服役状态评价模型构建方法,并以测点偏差度表征型架作业期初始服役状态的优劣(详见2.1节);同时从人、机、料、法、环等多源层面分析盒式连接可重构型架稳定性影响因素,并提出稳定性熵的概念以表征作业期内服役状态的“退化”程度(详见2.2节)。最终融合两者构建盒式连接可重构型架模块服役稳定性评价模型,以实现准确、高效地稳定性评估(详见2.3节)。
2 基于模块服役状态的盒式连接可重构型架服役稳定性评估方法
盒式连接可重构型架具有模块化特征,其优势不仅在于设计、安装阶段可以实现基于模块化的快速配置和搭建,而且在服役和维修阶段也可实现基于模块的稳定性评估和维修(更换),有利于及时发现问题并针对性维护。因此,提出如图2 所示的基于模块服役状态的盒式连接可重构装配型架稳定性评估框架流程。
如图2所示,盒式连接可重构型架稳定性评估过程由空置期服役状态评估、作业期服役状态退化程度评估和稳定性综合评估3部分组成。空置期主要基于型架关键测量特性构建服役状态评价模型,对测量数据进行处理,以定量表征模块空置期服役状态的优劣;作业期首先是对盒式连接可重构型架稳定性影响因素进行数值化表示,并利用稳定性熵表征在一定时间内模块作业期初始服役状态的退化程度;综合评估是融合上述两种服役状态评估数据构建模块服役稳定度,以评估型架稳定性的优劣。
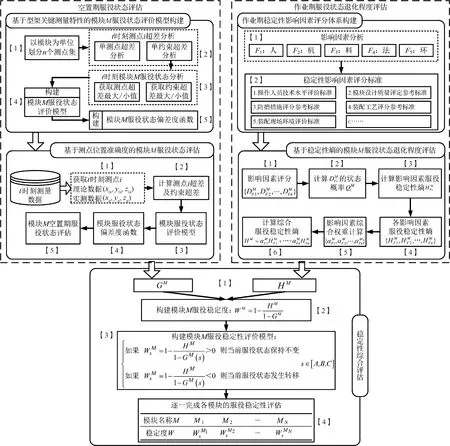
图2 盒式连接可重构型架稳定性评估框架流程Fig.2 Flowchart for stability evaluation of box-joint reconfigurable jig
2.1 基于型架关键测量特性的空置期服役状态评估
飞机制造过程中,若某个特性的改变对飞机产品的互换协调性产生巨大影响,那么这个特征即为关键特性(Key Characteristics, KCs)[16]。陈哲涵等[17]在考虑装配工艺及现场测量条件下提出了关键测量特性(Key Measurement Characteristics, KMCs),旨在降低测量成本和缩短测量周期。由于飞机装配型架的应用是保证飞机产品的装配精度,所以对产品互换协调性产生巨大影响的飞机产品关键测量特性可对应到装配型架上,即通过飞机产品关键测量特性(Product KMCs),就能得到型架关键测量特性(Jig KMCs),如图3所示。
图3表示由产品关键测量特性映射为型架关键测量特性的过程。图3左侧所示为依托产品结构形成的产品关键测量特性树,右侧所示为产品关键测量特性映射得到的依托型架结构形成的型架关键测量特性树。例如保证外形的卡板轮廓度,保证长桁位置的定位器位置度,以及保证各个部件间交点处互相协调准确的接头定位器交点孔同轴度等。目前,航空工业中采用基于坐标测量原理的数字化测量系统对型架关键测量特性进行监控,因此需要依据装配工艺与企业数字化测量能力,将关键测量特性进一步分解为目标测量点,称为关键测量点集,其空间坐标测量结果是对型架空置期进行服役状态监测的原始数据,包括理论数据(Nominal Data)和测量数据(Measured Data)。
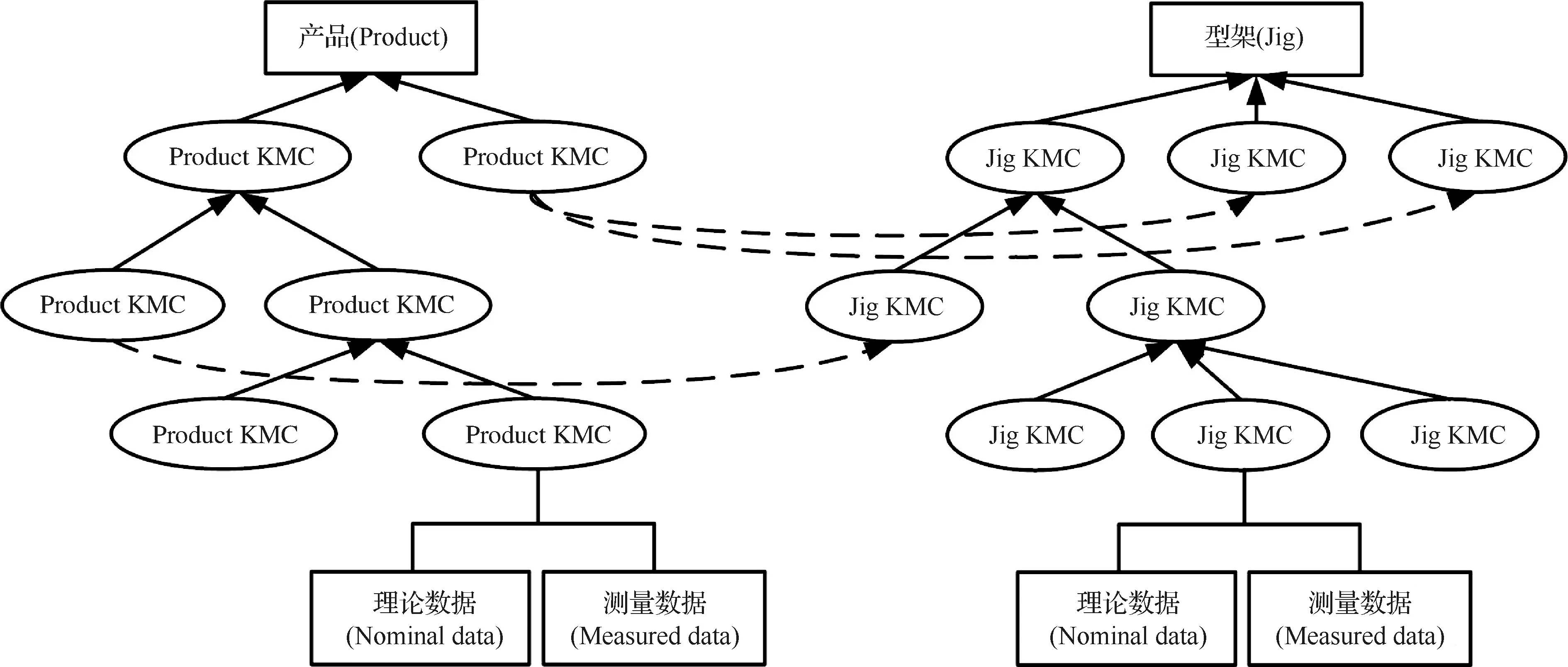
图3 产品关键测量特性与型架关键测量特性之间映射关系Fig.3 Mapping relationship between Product KMC and Jig KMC
根据上述原始数据并结合盒式连接可重构装配型架模块化特征,首先将型架划分为N个模块,记为{Mu|u=1,2,…,N}。以某型垂尾装配型架为例示意,如图4中上半部分所示为型架组成结构的模块化划分标准。然而该划分标准在稳定性评估中存在一些弊端,例如由于模块上无测量点导致无法检测该模块的位置精度等。故以上述模块化划分标准为基础,并面向型架的稳定性评估,提出如下3条划分准则以构建模块Mu。
准则1模块功能独立性,指型架中同类模块需按照具体应用功能进行再划分。如图4中某型垂尾装配型架可将定位器模块细分为1号肋定位器(No.1 Rib Locator)、后梁定位器(Rear Spar Locator)、卡板定位器(Board Locator)、前梁定位器(Front Spar Locator)及根肋定位器(Root Rib Locator)等。
准则2模块功能完整性,指型架中将协作实现同一功能的不同模块需划分为同一模块。如图4中各类定位器需要与盒式连接共同作用,实现飞机产品零件的定位功能,因此将定位器与盒式连接划分为同一模块。
准则3模块位置可测性,指型架中将无测量点的模块与有测量点的模块划分为同一模块,以原测量点作为新模块位置的测量基准,从而实现基于其测量值的无测量点模块位置的间接表征。如图4中将有测量点的骨架模块与无测量点的地脚支撑模块划分为同一模块等。
因此,以某型垂尾装配型架为例,其模块划分如图4中下半部分所示。基于上述模块划分结果,将每个模块上的测点划分为一个测点集,然后构建基于测点绝对位置准确度和测点间相对位置准确度的模块服役状态评价模型,以描述其从健康到失效劣化的过程。最后基于此模型构建测点偏差度表达函数,以表征某一时刻服役状态转移的可能性。
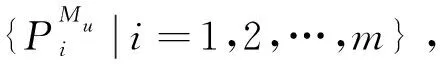
2.1.1 测点超差分析
(1)
测点超差可通过式(2)计算获得:
(2)
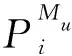
则t时刻模块Mu中所有测点超差值可记为{ξti|i=1,2,…,m}。
2.1.2 测点约束超差分析
测点约束超差分析旨在表征测点间的相对位置准确度是否满足阈值要求。它能更好的表达测点之间的关系,尤其对于可重构装配型架,不同模块间的测点相对位置准确度能直观反映型架组成模块之间装配的相对位置精度,从而反映了基于此模块定位的待装组件装配应力的大小。测点间主要的约束包括距离约束、共线约束及对称约束,假设dist(·)为距离计算函数,则记约束实测误差为

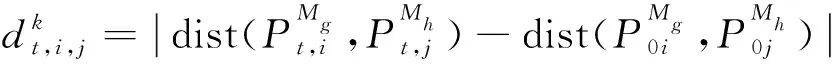
(3)

(4)

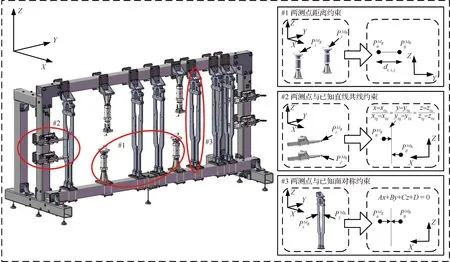
图5 测点和之间约束超差分析原理图Fig.5 Schematic diagram of constraint out-tolerance analysis between
(5)
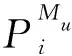
则测点约束超差可通过式(6)计算获得:
(6)
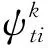

2.1.3 测点位置可行域求解
测点位置可行域是指测点测量数据满足公差要求的可行位置集合。若测点实测坐标处于位置可行域内,则认为该测点满足定检要求。目前航空工业中,测点位置可行域的设定仅考虑了测点绝对位置公差带,而忽略了测点相对位置约束关系的影响,不利于测点位置精度的评估。因此综合考虑测点绝对位置公差与相对位置公差,构建合理的测点位置可行域是实现模块服役状态评估的必要条件。
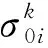
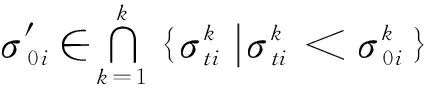
(7)
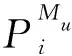

图6 测点的绝对位置可行域与相对位置可行域Fig.6 Feasible region of absolute position and relative position of
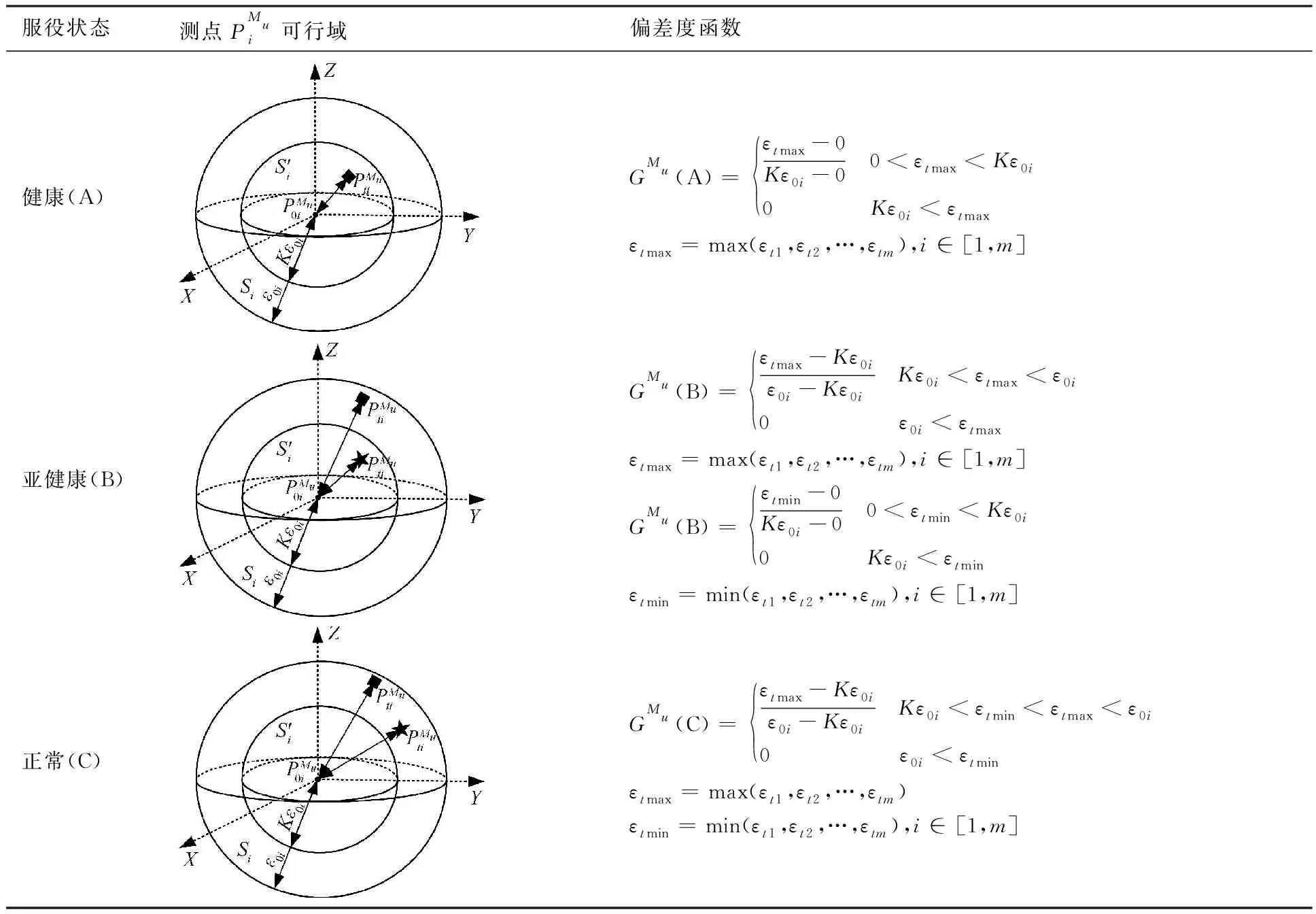
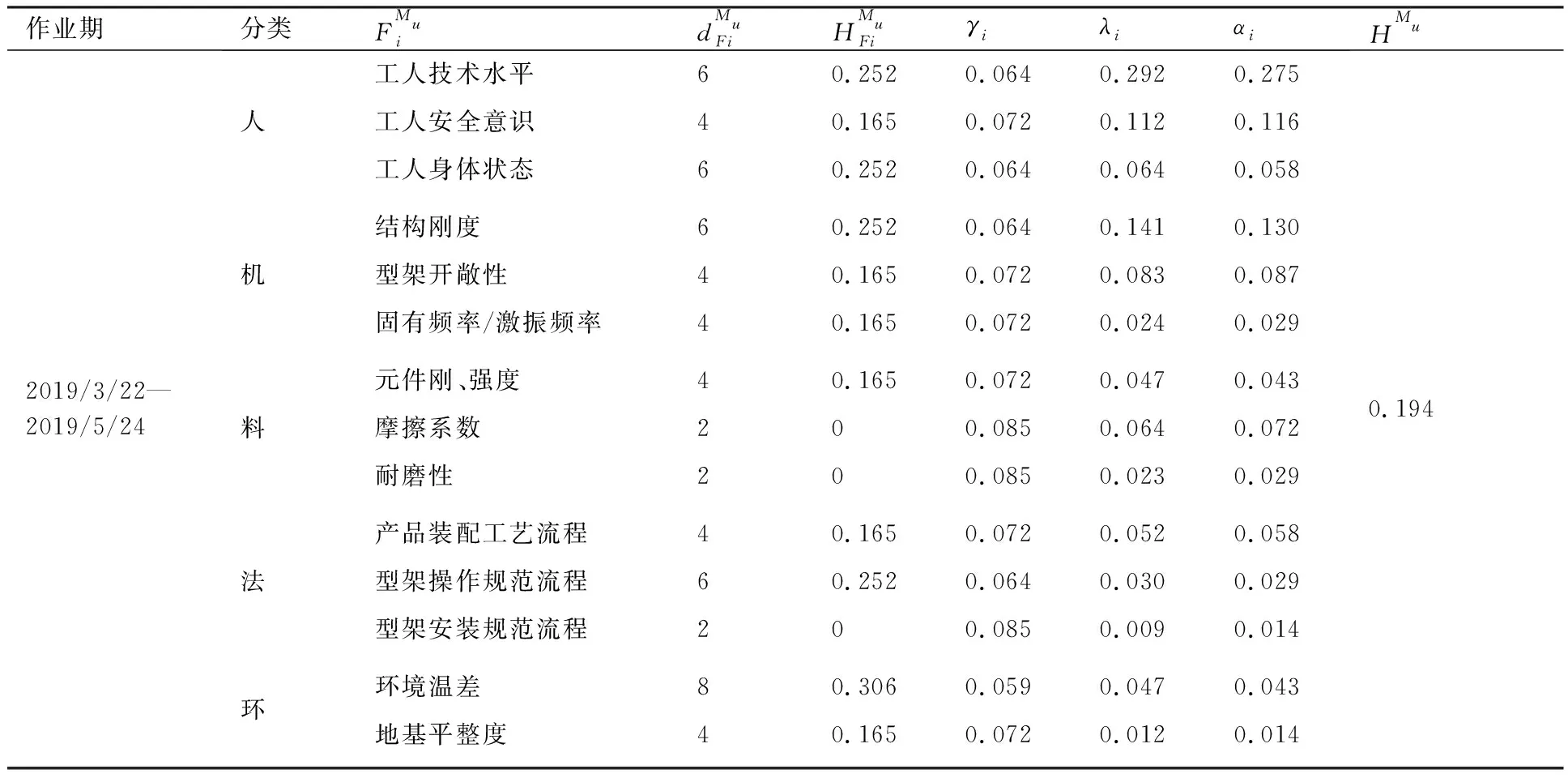
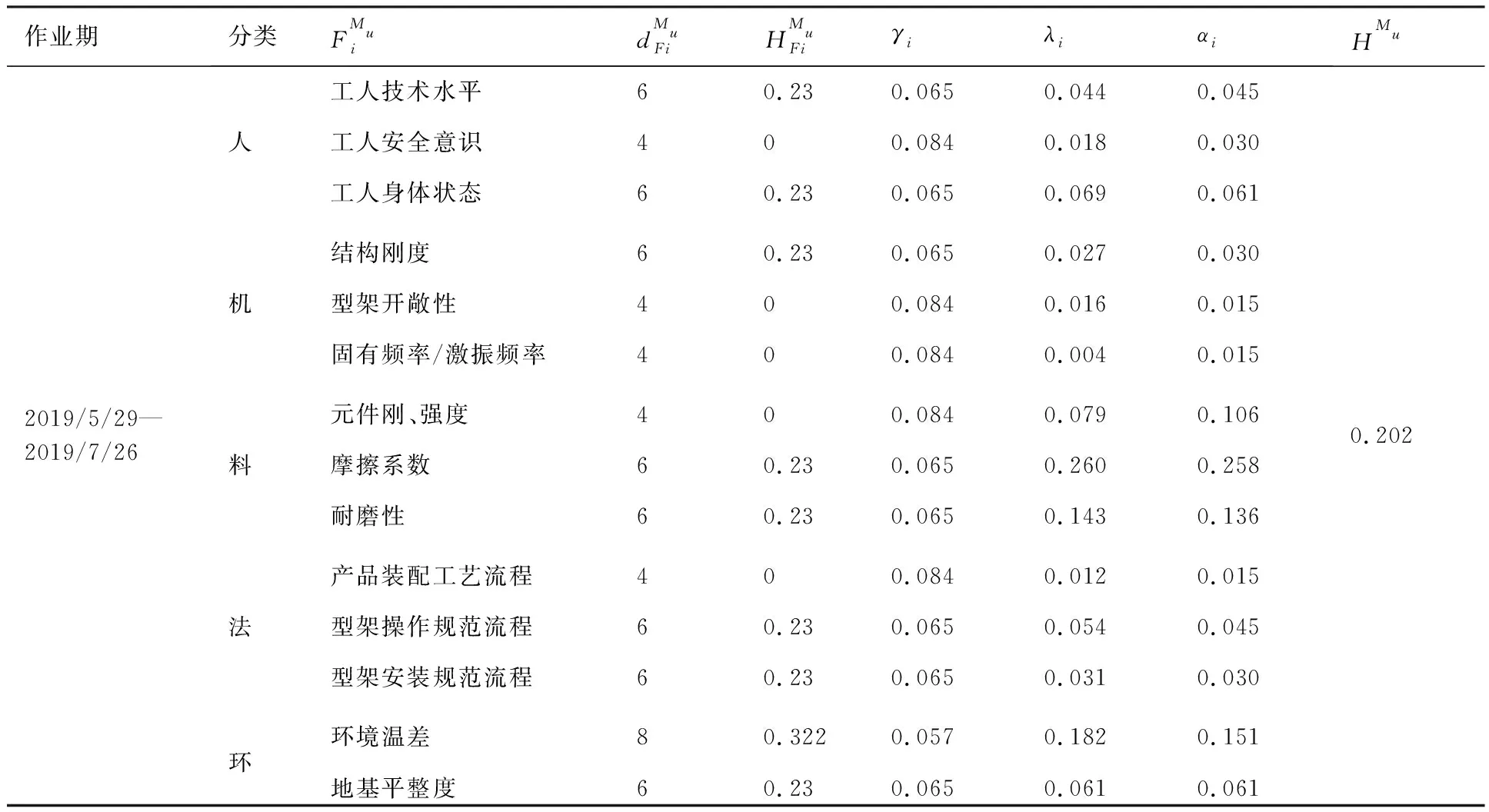
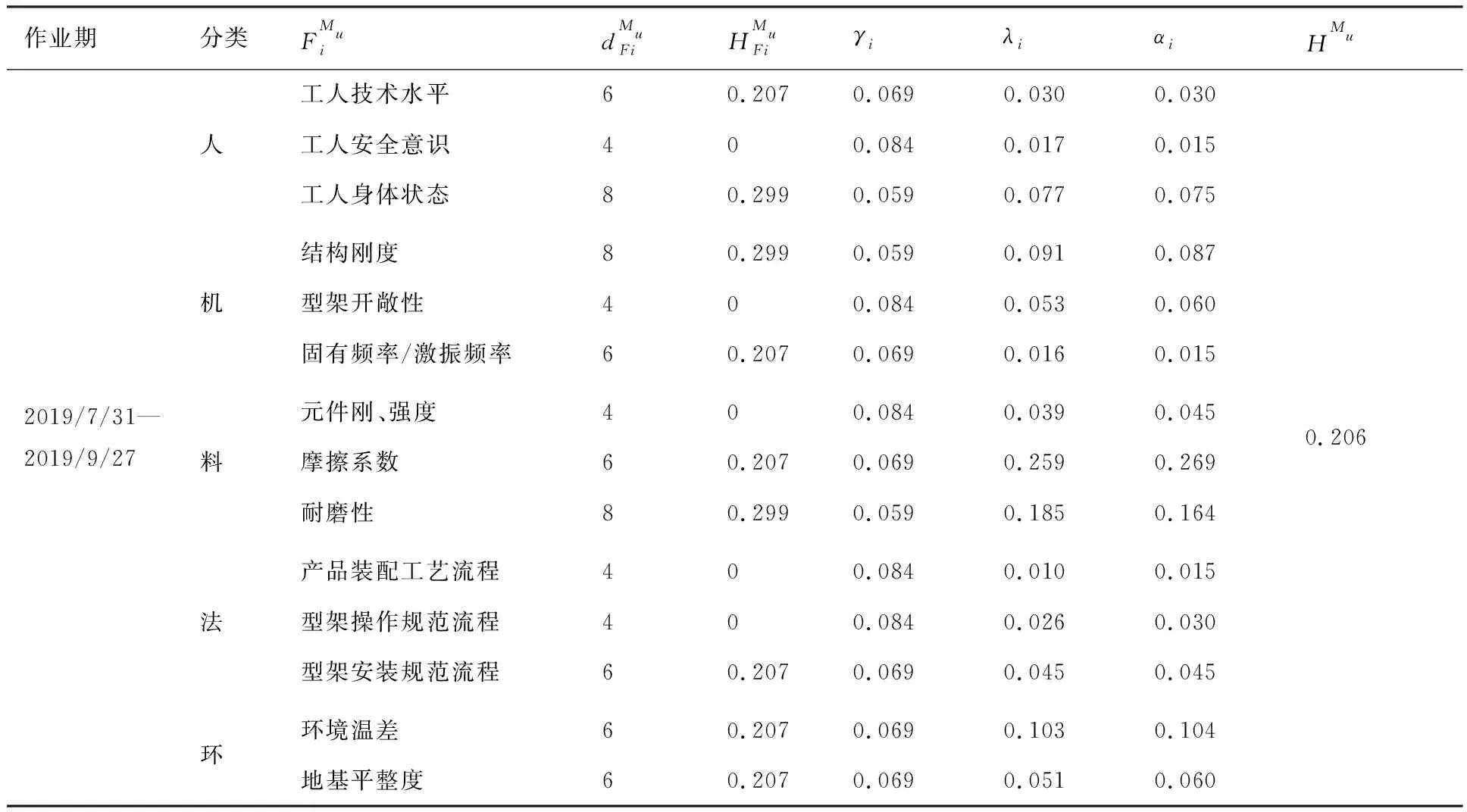
其中σ′0i=Kε0i,0 2.1.4 基于测点位置准确度的模块服役状态评价模型构建 表1 盒式连接可重构装配型架模块服役状态划分等级 在已知服役状态的基础上,又构建了与样本容量无关的数字特征,即测点偏差度,以表征当前服役状态的优劣,不同的服役状态对应的偏差度函数不同,如表2所示。以t时刻空置期服役状态为健康状态为例,模块Mu中所有测点均属于可行域S′,其中误差最大值点偏移理论位置的距离与可行域S′范围的比值即为偏差度,记为GMu。 表2 不同服役状态所对应的偏差度函数Table 2 Deviation degree functions of different service states 偏差度越大,测点发生漂移的可能性越高,则型架进入作业期后出现服役状态转移的可能性越高;反之,偏差度越小,作业期内出现服役状态转移的可能性越低。因此,以偏差度作为空置期服役状态的度量,可为下一轮作业期内服役状态退化程度评估提供一个评价指标。 空置期服役状态评估仅是依靠测量所获取的准确数据完成了型架作业期初始服役状态的度量,由于型架在作业期内无法实时获取关键测点数据,因而难以实现通过测量数据描述型架服役状态的退化过程。故合理利用其它有效信息,如专家知识、型架有限元分析数据和历史型号产品在使用过程中留下的数据等,是解决盒式连接可重构装配型架样本数据匮乏的重要手段。因此,提出首先从人、机、料、法、环5个层面分析影响稳定性因素,并给出量化指标,然后结合其他有效信息完成型架作业期内的打分评定,最后提出稳定性熵的概念用以表征盒式连接可重构型架服役状态退化程度。 2.2.1 稳定性影响因素分析 盒式连接可重构装配型架服役稳定性主要受型架本身的装配质量和服役阶段中过程因素的综合影响。因此从人、机、料、法、环5个方面对稳定性影响因素展开溯源分析[18],并利用鱼骨图的形式表达,如图7所示。 图7 影响盒式连接可重构装配型架稳定性因素分析Fig.7 Analysis of influence factors of stability of box-joint reconfigurable assembly jig 1) 人(Man):在可重构装配型架的作业期内,飞机产品零组件的定位与装配主要由人工操作完成,装配人员的技术熟练度、身体状态、安全规范意识等因素影响型架的服役状态。 2) 机(Machine):可重构装配型架的结构设计对其自身稳定性的影响十分重要。骨架结构刚度影响定位点在产品装配过程中的定位精度,可通过有限元分析获取有效信息;飞机产品装配铆接时的激振频率对定位点漂移的影响;结构开敞性不好导致人员与型架碰撞等因素影响型架的服役状态。 3) 料(Material):可重构装配型架的主要特点是采用螺栓连接,依靠摩擦力保证定位元件的位置精度。因此在型架作业期内,螺栓的性能和骨架梁材料表面摩擦系数是保证可重构装配型架稳定性的重要因素。 4) 法(Method):可重构装配型架的安装工艺及其服役阶段的使用规范影响着型架的稳定性。如螺栓预紧力的大小未达到设计要求易导致盒式连接板松动,从而出现固定在连接板上的定位器产生漂移现象,影响稳定性。 5) 环(Environments):可重构装配型架服役阶段环境温度、湿度、地基平整度对稳定性有着重要影响。如温差变化显著易引起型架材料热胀冷缩,导致型架骨架变形和定位点漂移;地基下沉同样影响型架基准变化,导致定位点漂移。 基于上述5个方面的稳定性影响因素分析,分别给出具体因素的量化指标,采用十分制表示,其中10分表示该影响因素对稳定性影响最严重,0分表示最不严重,如表3所示。 表3中关键指标数据说明: 表3 稳定性影响因素评分标准Table 3 Scoring criteria of influencing factors of stability 1) 结构刚度(Structural Stiffness)的评分标准是依据历史相关数据而设定的,通常认为模块结构受力变形量超过0.1 mm,则会造成产品的定位超差,将0~0.1 mm的变形范围划分为五个等级,并分别与相应得分建立映射关系。当评定打分时,可利用型架模块的变形仿真分析数据进行评估; 3) 耐磨性(Abrasion Resistance)的评分标准是依据模块硬度值而设定的,硬度值越高,耐磨性越好。 4) 环境温差(Temperature Variations)的评分标准是参考历史相关数据而设定的[1,13],通常夏季一天之内温差变化约为10 ℃,厂房安装有空调,温差变化更小,更有利于保持型架稳定性。 2.2.2 稳定性熵计算 美国数学家Shannon[19]提出信息熵是信息无序度的度量,无序度越大,信息熵越高;无序度越小,则信息熵越小。王波和唐晓青[20]提出装配质量熵(Assembly Quality Entropy,AQE)的概念,描述了装配产品质量损失的大小,反映出装配过程中的实物质量损失和非实物潜在质量损失。通过对可重构装配型架服役过程及稳定性影响因素分析可知,在作业期内多种因素影响造成型架服役状态处于长期退化的过程,这种可重构装配型架服役状态的损失与装配质量熵的微观解释在思维方法上具有相似之处。因此,在参考和借鉴信息熵和装配质量熵定义的基础上,提出了型架稳定性熵的概念。 定义3稳定性熵是指在可重构装配型架服役阶段中其服役状态退化程度的一种量度,熵值越大,则退化程度越大,服役状态发生转移的可能性越大,稳定性越差,则稳定性熵定义为 H(Fi)=(-1/lnn)QilnQi (8) 式中:Fi表示影响可重构型架服役稳定性因素,n表示影响因素总数,则记{Fi|i=1,2,…,n};Qi表征第i个因素对稳定性的影响程度。 其综合稳定性熵为 (9) 因此,可重构装配型架模块Mu的稳定性熵计算流程为 表4 不同级别专家话语权占比重 1) 同一级别专家的每项影响因素得分求平均值,得到每一级别的每项影响因素得分。则 (10) 2) 根据各级别话语权占比重Z1,Z2,…,Z5计算各影响因素的得分。即 (11) (12) 4) 进行标准化处理以消除不同度量标准和方法的影响,采用直线型无量纲化法中的极值法进行数据处理[21]。 (13) 步骤3第i个因素对模块Mu稳定性的影响程度值定义为 (14) (15) 2.2.3 影响因素的综合权重计算 (16) 综合主、客观权重,在λi和γi的基础上,得到第i项影响因素的综合权重为 (17) 盒式连接可重构型架是由不同模块搭建而成,任何一个模块的功能失效都将导致型架的服役期结束。因此针对盒式连接可重构型架各模块的服役状态评估,更能快速、准确地发现型架服役过程中的稳定性问题,更具有评估意义。故综合考虑空置期服役状态和作业期服役状态退化程度的共同影响,提出融合测量数据及多源稳定性影响因素分析的盒式连接可重构型架模块稳定性评估方法,该方法充分利用测点的测量数据和稳定性影响因素评定数据,构建盒式连接可重构型架模块的服役稳定度函数: (18) 式中:WMu表示模块Mu的服役稳定度;偏差度GMu表征模块Mu空置期服役状态的优劣,GMu越小,则型架进入作业期后出现服役状态转移的可能性越低,稳定性越好;WMu还与作业期内服役状态退化程度有关,以稳定性熵HMu度量,HMu越小,表示受噪声影响所导致的服役状态波动程度越小,保持服役状态的能力越强,稳定性越好。基于服役稳定度构建了盒式连接可重构型架模块的服役稳定性评价模型如式(19)所示: (19) 以某型垂尾盒式连接可重构装配型架中后梁定位器模块为例进行服役稳定性评估实验验证,如图4所示,其上3个测点分别是OTP-2、OTP-3和OTP-4,其理论数据如表5所示(由某飞机公司提供并已经过处理)。为了提高空置期实测数据的准确度,尽量减少其受人、机、料、法、环等方面影响,在测量过程中,实施了诸如提高检测人员的资质水平、保证测量仪器的使用状态、提高测点位置材料的耐磨性、针对测量结果采取温度补偿、控制作业现场的温度及避免地面的过大振动等相应措施。因此,当前空置期测点数据可视为综合以上5个方面影响下的型架服役状态的数字表征,可直接用于反映型架当前服役状态的优劣。 实验过程历时3个时间段: 表5 后梁定位器模块测点集理论数据Table 5 Theoretical data of from rear spar locator module mm 表6 不同级别专家针对型架开敞性影响因素评分 根据式(11)计算可得 0.28×4+0.36×2=3.2 (20) 根据式(12)计算可得 (21) 表7 后梁定位器模块作业期内影响因素评定及稳定性熵计算(第1个时间段) 表8 影响因素主观权重计算的判断矩阵(第1个时间段)Table 8 Judgment matrix of subjective weights of influencing factors (The first time period) 0.806>0 (22) 表9 t1时刻后梁定位器模块测点集实测数据Table 9 Measured data of from rear spar locator module at t1 mm 第二个时间段:2019/5/27~2019/7/26。由上述分析结果可知,后梁定位器模块空置期t1时刻服役状态为健康状态,则根据健康状态的偏差度计算公式得GMu(A)=0.64。与第1个时间段相比,该时间段的作业期内摩擦系数、耐磨性、螺栓预紧力及地基平整度等影响因素发生变化: 1)由于型架长期、连续使用而导致模块材料磨损,造成摩擦系数及耐磨性降低。 2)同时也导致型架装配工艺中螺栓松动,造成预紧力不足。 3)该时间段春夏交替,温差变化造成地基平整度降低。 因此,影响因素评定及稳定性熵计算如表10所示,其中影响因素评分参考表3,主观权重计算的判断矩阵如表11所示。 表10 后梁定位器模块作业期内影响因素评定及稳定性熵计算(第2个时间段) 表11 影响因素主观权重计算的判断矩阵(第2个时间段)Table 11 Judgment matrix of subjective weights of influencing factors (The second time period) 采用相同的计算方法,并将计算结果GMu(A)=0.64及HMu=0.202代入式(19)得 (23) 表12 t2时刻后梁定位器模块测点集实测数据(单位:mm)Table 12 Measured data of from rear spar locator module at t2 第3个时间段:2019/7/29—2019/10/9。 根据上述分析结果可知,后梁定位器模块空置期t2时刻服役状态为健康状态,则根据健康状态偏差度计算公式得GMu(A)=0.84。与第2个时间段相比,该时间段的作业期内工人身体状态、结构刚度、耐磨性及温差等影响因素发生变化: 1) 该时间段夏季气候闷热,造成工人身体状态欠佳。 2) 型架长期、连续使用造成结构刚度减小。 3) 型架长期、连续使用造成材料耐磨性降低。 4) 夏季温差变化小。 因此,影响因素评定及稳定性熵计算如表13所示,其中影响因素评分参考表3,主观权重计算的判断矩阵如表14所示。 表13 后梁定位器模块作业期内影响因素评定及稳定性熵计算(第3个时间段) 表14 影响因素主观权重计算的判断矩阵(第3个时间段)Table 14 Judgment matrix of subjective weights of influencing factors (The third time period) 采用相同的计算方法,并将计算结果GMu(A)=0.84及HMu=0.206代入式(19)得 (24) 表15 t3时刻后梁定位器模块测点集实测数据Table 15 Measured data of from rear spar locator module at t3 mm 1) 结合盒式连接可重构型架模块化特征提出针对各模块服役状态的稳定性评估方法,能够更快速、准确地发现型架服役过程中的稳定性问题,便于及时采取针对性维护,更具有评估意义,为盒式连接可重构型架的推广应用提供理论基础。 2) 基于型架关键测量特性分析构建了包含4种服役状态的评价模型,并提出了相应的偏差度函数,实现了盒式连接可重构型架空置期服役状态评估及退化过程的描述。 3) 从人、机、料、法、环5个层面分别给出型架稳定性影响因素的量化指标并构建了评分体系,在此基础上提出稳定性熵的概念,实现了盒式连接可重构型架作业期服役状态退化程度的评估。 4) 提出的融合测量数据与多源稳定性影响因素分析的盒式连接可重构型架模块稳定性综合评估方法既充分考虑了空置期服役状态对盒式连接可重构型架稳定性的影响,又考虑了作业期因缺少测量数据而难以准确评估服役状态的不足,相比传统的定检方法能够更简捷、有效地完成型架整个服役过程的稳定性评估,有助于避免型架在作业期发生稳定性问题,更具指导意义。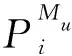

2.2 基于稳定性熵的作业期服役状态退化程度评估


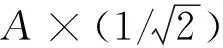
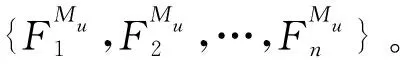


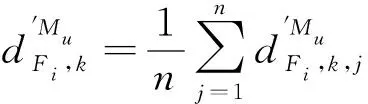
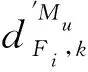
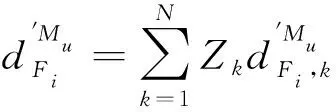
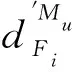


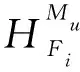
2.3 融合测量数据与多源影响因素分析的模块稳定性综合评估


3 实验验证
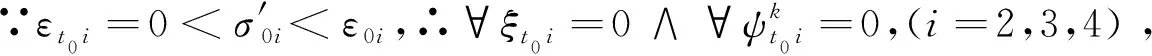
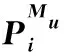


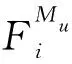


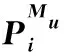


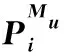


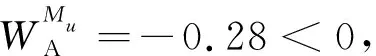
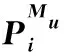
4 结 论
——以徐州高层小区为例

