DIMA架构下飞机全电刹车系统故障传播行为分析与评估
阎芳,向晨阳,董磊,*,王鹏
1. 中国民航大学 民航航空器适航审定技术重点实验室,天津 300300
2. 中国民航大学 天津市民用航空器适航与维修重点实验室,天津 300300
3. 中国民航大学 适航学院,天津 300300
分布式综合模块化航电系统(Distributed Integrated Modular Avionics,DIMA)是当前航空电子系统架构的主流发展趋势之一,不同于综合模块化航空电子(Integrated Modular Avionics,IMA)体系架构围绕包含所有共享计算资源单一机柜的设计理念,DIMA在此基础上进行了扩展,允许计算资源分布在飞机的不同部位,设计理念更加灵活先进,典型应用机型包括A350 XWB[1-4]。得益于DIMA开放的系统架构,欧盟FP7框架下科技研究项目SCARLETT(Scalable & Reconfigurable Electronics Platforms and Tools)[5-6]提出了集成机轮刹车、电源系统等非传统航电功能的DIMA架构设想。其中项目合作方梅西埃公司首次提出面向IMA架构下的飞机全电刹车系统架构设计方案,从系统的研制保证等级、计算资源配置、数据传送以及系统输入输出接口等方面论证了DIMA架构下全电刹车系统功能、性能需求以及当前的技术限制[7-9]。DIMA架构下的飞机全电刹车系统是未来刹车系统设计的主流趋势。
目前针对常规全电刹车系统的故障传播行为分析与评估方法总体可分为人工分析和智能诊断分析法,前者的应用依赖于实操者工作经验与主观判断;后者主要涵盖基于故障信息监控和基于训练模型的故障传播分析与评估方法,能够实现故障传播行为的自动化分析与评估[10-13]。随着DIMA计算资源共享平台的引入,应考虑到各核心处理模块(Core Processing Module,CPM)间的高度耦合,其次传感器本身易受周围环境影响,使得采集的信号出现偏差,从而导致分析结果出现偏差,同时故障模型库的建立过程较为复杂,模型的训练成本较高。为解决上述问题,学术界和工业界通过引入Petri网[14]、马尔可夫过程(Markov Process,MP)[15]、元胞自动机(Cellular Automata,CA)[16]以及包括规则网络、小世界网络和随机网络等具有拓扑结构特征的复杂网络[17-18],建立故障传播模型研究复杂系统的故障传播行为。Petri网依赖于系统结构模型以模拟相互依赖关系,不适用于精细建模或大型复杂系统,建模资源不易重用[14,19];文献[15]通过引入连续时间马尔科夫链开展了可重构IMA系统可靠性分析,然而并未考虑系统各CPM间耦合关联分析;元胞自动机模型主要关注系统基本组件的状态变化,无法定量系统结构模型有向边对系统的影响程度[16];小世界网络介于规则网络和随机网络之间,建模过程受限于DIMA架构下全电刹车系统特征路径长度和聚类系数,转化过程复杂[17]。上述方法缺乏对系统内部各模块间的耦合关系的定量分析与评估,并不适用于DIMA架构下全电刹车系统的故障传播行为分析与评估。
基于上述情况,本文提出一种面向DIMA架构下全电刹车系统的故障传播行为分析与评估方法。首先构建DIMA架构下全电刹车系统层次模型,输出系统映射关联矩阵,在此基础上开展系统资源层耦合关联分析,导出耦合关联矩阵以指导后续故障概率模型和系统故障传播结构模型的建立,并在此基础上结合系统故障传播概率与边缘介数,计算CPM节点综合故障传播强度,以识别故障传播关键路径,完成DIMA架构下故障传播行为分析。最后通过实例分析,验证所提方法的正确性与合理性。
1 DIMA架构下飞机全电刹车系统架构
基于ARINC 653的综合模块化航空电子(IMA)体系架构被广泛应用于现代民用和军用飞机的设计中[20]。IMA以共享资源和标准化组件为核心,是一个用于执行飞机航电系统功能的安全关键公共计算平台,在减少嵌入式设备数量的同时,以推进航电系统标准化进程,但其功能和速度有限,仍无法满足日益增长的使用需求。DIMA作为现代航空电子系统架构最新的发展形式,其设计理念相较于IMA更加灵活,更加注重系统各模块互换性、可扩展性和适应性,在此开放性系统架构背景下,飞机机电、航电等系统功能的划分逐渐相互融合渗透,传统非航电系统,如空调、电源、燃油以及起落架等系统也将逐步纳入DIMA平台[7-8]。针对实时性较强的飞机全电刹车系统,在考虑防滑功能的前提下,低延迟、低抖动以及确定性的数据传送必不可少,随着DIMA平台的引入,可为其提供强大的计算资源,以满足全电刹车系统的高实时性能需求。本文结合DIMA系统架构特点,提出了DIMA平台下全电刹车系统分层架构,如图1所示。

图1 DIMA架构下飞机全电刹车系统架构Fig.1 Architecture of aircraft all-electric brake system under DIMA architecture
面向DIMA的全电刹车系统分层架构设计,包括系统任务层、系统功能层、资源层以及执行层。从架构的角度来看,系统功能层由相应子系统的功能组成,上述功能形式的抽象有利于降低系统的复杂性;资源层通过强大的公共计算处理资源来实现控制算法快速加载与控制指令的输出,同时资源的调度依托于系统功能层向资源层的映射活动与规则,主要包括功能到资源的映射,信号到链路的映射;执行层主要接收来自机载总线的指令信号,完成系统的指令动作,并向资源层核心处理模块反馈相应的系统执行参数,实现系统的闭环控制。
1) 系统任务层
根据Harmony-SE系统工程理论[21],系统架构模型的构建依赖于特定的任务需求背景,即通过对涉众需求的捕获分析完善,构建系统的用例场景,以定义所需的系统功能以及顶层系统任务与系统功能的映射关系,这些用例场景即可定义为系统的任务层。
2) 系统功能层
从系统设计的角度出发,根据飞机全电刹车系统相关的设计规范[12,22-23],包括资源需求,接口需求、性能需求和安全性需求等,结合DIMA平台特征,梳理飞机全电刹车系统典型功能,主要包括信息显示与告警功能与系统控制功能。同时考虑后续功能层到资源层的映射,在顶层功能基础上进一步分解,包括自动刹车、人工刹车、地面停机刹车、机轮空中制动以及机组告警等功能,以指导后续全电刹车系统资源层的耦合关联分析。
3) 资源层
上述功能的实现需调用资源层不同的核心处理模块(Core Processing Module,CPM),其为全电刹车系统功能算法的实现或高度耦合的控制循环提供计算资源。此模块按应用分区驻留相关功能应用,主要包括制动参数解算、刹车指令的输出、防滑刹车算法加载、刹车模式选择、告警处理、机内自检BIT、刹车监控软件、刹车压力显示、机轮速度显示等。考虑简化后续全电刹车系统层次建模与耦合关联分析,定义每个分区运行单个功能应用,无备份冗余模块,不考虑系统动态重构情况。针对资源层不同CPM间的故障传播,本文采取较为保守的配置方式,假定全电刹车系统资源层CPM分区处于“全连通”状态[1],即认为资源层任意两CPM间存在故障传播路径。针对功能层到资源层的映射,应考虑资源层不同CPM间的耦合关系,即不同的系统功能可映射至同一CPM,各CPM以及远程数据采集器(Remote Data Concentrator,RDC)之间通过航空电子全双工交互式以太网(Avionics Full Duplex Switched Ethernet,AFDX)进行数据通信。
4) 执行层
执行层负责接收刹车指令,完成刹车动作,由远程数据采集器(Remote Data Concentrator,RDC)、机电作动控制器(Electro-Mechanically Actuation Controller,EMAC)、机电作动器(Electro-Mechanical Actuator,EMA)、机轮速度传感器、刹车压力传感器以及机轮组成,其中EMAC单元是执行层核心部分,负责接收刹车指令以及电机的伺服控制,通过高速现场总线与RDC相连,在确保低抖动与低时延的情况下,输出EMA中刹车电机控制信号,驱动EMA机电作动器输出刹车力。
2 DIMA架构下全电刹车系统故障传播结构模型
DIMA架构下全电刹车系统故障传播行为分析与评估流程主要分为3个阶段。首先,结合DIMA架构下全电刹车系统架构特征,从系统任务层、功能层以及资源层构建系统层次模型,输出系统不同层级间的映射关联矩阵M,完善系统不同层次间的映射关系,以指导后续全电刹车的耦合关联分析,耦合关联分析包括直接耦合和间接耦合分析,基于上述系统映射关联矩阵得出系统资源层直接耦合矩阵,在此基础上引入Floyd算法[24],计算间接耦合矩阵以及路由矩阵;第二,故障概率模型的建立,通过量化系统耦合关联程度构建失效严重程度矩阵,结合隶属函数输出各CPM耦合失效分布函数,并结合上述路由矩阵建立全电刹车系统故障传播结构模型;最后在基于耦合关联分析的故障概率模型的基础上,考虑资源层各CPM节点自身和有向边的故障影响程度,引入概率重要度、临界重要度以及耦合度函数,建立系统故障传播概率模型,输出故障路径传播概率,结合系统边缘介数建立故障传播强度模型,完成DIMA架构下全电刹车系统的故障传播行为分析。全电刹车系统故障传播行为分析与评估流程如图2所示。

图2 DIMA架构下飞机全电刹车系统故障传播行为分析与评估Fig.2 Fault propagation behavior analysis and evaluation of aircraft all-electric brake system under DIMA architecture
2.1 全电刹车系统层次模型
系统模型的建立始于涉众需求的捕获,通过需求分析导出系统的用例场景[21]。从系统黑盒设计的角度分析,系统的用例场景可定义为系统的任务视图或任务层,在此基础上,进行系统功能分解,导出系统功能层。全电刹车系统功能的实现需要制动参数解算模块、监控以及告警模块等物理资源的支持,即需要定义系统的任务或功能层到资源层的配置和映射关系。结合DIMA平台下全电刹车系统分层架构,从层次分解的角度[25-26],结合拓扑建模理论,建立基于任务-功能-资源层的DIMA架构下全电刹车系统层次模型。在此给出如下定义:
1) 定义T={t1,t2,…,tk}为系统任务层元素集合,k为任务个数。
2) 定义F={f1,f2,…,fm}为系统功能层元素集合,m为系统功能个数。
3) 定义D={d1,d2,…,dn}为系统资源层元素集合,n为资源层CPM个数。
通过对系统层次架构分析,定义如下映射关联矩阵Mtf表示系统任务层与功能层元素间的映射关系。
(1)
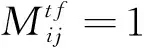
同理,功能-资源映射关联矩阵Mfd为

(2)
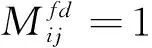
2.2 全电刹车系统故障传播结构模型
由于DIMA平台资源共享的特点,DIMA平台下全电刹车系统资源层中各CPM之间的复杂关联耦合,不同的CPM可服务于相同的系统功能,各CPM之间存在直接或间接地数据传递,进而导致局部故障通过故障传播对整个系统产生影响,导致计算分析结果与实际运行产生较大偏差。建立基于耦合相关性的故障概率模型是分析和量化系统故障传播结构模型的基础。
2.2.1 全电刹车系统资源层耦合关联分析
耦合关联是指系统中各要素因任务、功能和安全性需求而产生的各种关联关系,如资源重用、信息传递、数据共享等[19]。耦合相关性的强弱可以通过耦合程度来量化。DIMA平台下全电刹车系统资源层耦合形式包括直接耦合与间接耦合,系统某一功能层元素可映射到资源层不同的CPM节点,造成资源层CPM之间的信息传递,即引入了不同CPM间的直接耦合关系。同时,由于DIMA平台下,系统计算资源共享形式的引入,导致资源层CPM节点间更为复杂的间接耦合关联。根据文献[25],分别定义直接耦合矩阵和间接耦合矩阵,定量描述DIMA平台下全电刹车系统层次结构模型中的直接耦合和间接耦合关系。
1) 直接耦合矩阵
直接耦合矩阵表示资源层中各CPM节点存在的直接信息交互或被同一系统功能层元素映射。根据功能-资源映射关联矩阵Mfd,可得直接耦合矩阵为
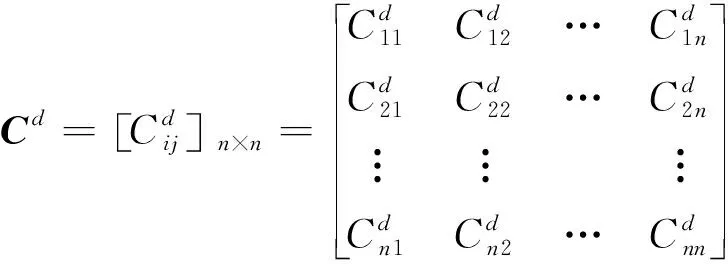
(3)

2) 间接耦合矩阵
间接耦合矩阵是直接耦合矩阵的扩展,表示各CPM间的间接耦合关系。针对DIMA平台下全电刹车系统等复杂关联系统,由于资源共享形式的引入,根据级联失效理论[27],单个CPM的失效可通过故障传播对整个系统产生影响,有必要定义间接耦合矩阵来评估间接耦合的潜在风险。根据文献[19,25],在直接耦合矩阵的基础上,引入Floyd算法计算资源层各CPM间故障传播路径,其基本过程是以直接耦合矩阵Cd为输入,递归更新n次[24]。每个更新过程引入一个新的过渡节点来比较传播路径是否优化,直到引入所有节点为止,得出间接耦合矩阵Cu,即
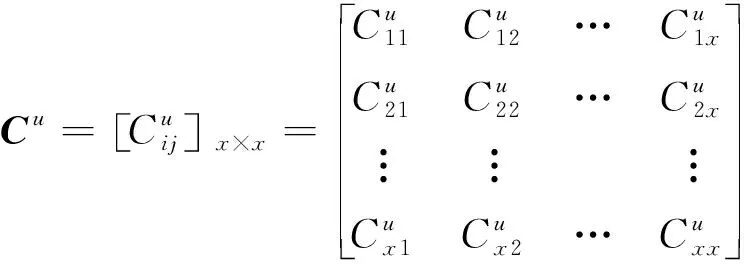
(4)
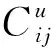
2.2.2 全电刹车系统故障传播结构模型的建立
同上利用Floyd算法得到路由矩阵Cr,即

(5)

G=[D,E]
(6)
式中:节点集D={d1,d2,…,dn}表示全电刹车系统资源层各CPM,n为资源层CPM个数;有向边集E={e1→2,e2→3,…,em→n}表示各CPM间的故障传播关系。
3 DIMA架构下全电刹车系统故障传播行为分析
3.1 基于耦合关联分析的故障概率模型
1) 耦合关联度风险量化描述
全电刹车系统资源层各CPM的失效严重程度会随着间接耦合度非线性降低,即失效严重程度随故障传播步骤的增加而降低。根据文献[25],失效严重程度即为耦合关联度的风险量化形式,定义失效严重程度矩阵,即

(7)
式中:Sij为失效严重程度,取值为1~5。根据文献[28-29],建立间接耦合度与失效严重程度的映射关系,给出隶属函数,即

(8)
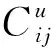
2) 全电刹车系统资源层故障概率模型
基于失效严重矩阵,定义全电刹车系统资源层各CPM耦合关联修正系数,即
ε=[ε1,ε2,…,εi,…,εn]
(9)
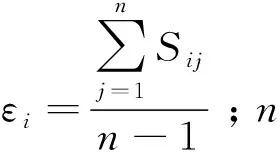
根据文献[6],假定资源层各CPM服从指数分布,资源层节点di失效率为λi,耦合失效分布函数为
Fi(t)=1-e-εiλit
(10)
式中:t为时间变量;εi为耦合关联修正系数。
3.2 全电刹车系统故障传播概率模型
在全电刹车系统耦合失效概率模型的基础上,引入概率重要度与临界重要度,以量化资源层各CPM节点自身的故障影响程度;其次,通过耦合度函数计算各节点有向边的故障影响程度;最后结合系统故障概率模型,输出系统故障传播概率模型。
1) 系统资源层CPM节点概率重要度
概率重要度最早由Birnbaum提出,其主要体现系统某一部件的失效对系统整体的影响程度,资源层CPM节点概率重要度计算公式为[30]

(11)
式中:i=1,2,…,n,其中n为资源层CPM个数,FZ(t)为全电刹车系统资源层整体失效分布函数,Fi(t)为资源层节点di失效分布函数。
在不考虑动态重构和备份冗余的情况下,系统资源层某一CPM出现故障时,都有可能导致全电刹车系统功能异常,因此本文将各CPM间关系视为串联关系,故全电刹车系统资源层整体失效分布函数为

(12)
2) 系统资源层CPM节点临界重要度
临界重要度最早由Lambert和Yadigaroglu提出,反映系统节点失效概率变化率对系统整体失效率变化量的影响程度,各CPM节点临界重要度的计算公式为[31]
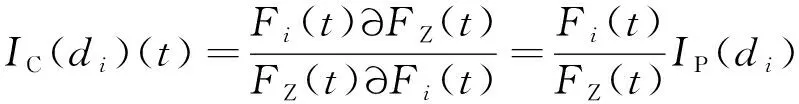
(13)
3) 系统CPM节点间有向边影响度计算
针对DIMA架构下全电刹车系统,资源层某一个CPMdi发生故障,并通过两节点间的有向边ei→j将故障传递到CPMdj,即di与dj间有向边影响程度体现了失效节点CPMdi对下游相邻节点CPMdj的影响程度。根据文献[32],引入耦合度函数计算有向边的故障影响程度,其为时间t的函数,即
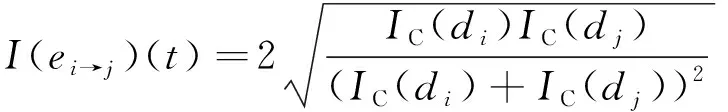
(14)
式中:I(ei→j)为有向边故障影响程度,其值取0~1,值越大,对故障传播的贡献越大。
4) 故障传播模型的建立
资源层CPM节点的状态取决于其自身的失效概率和上游CPM节点故障对其的影响,即两节点间有向边的故障影响程度。根据文献[33],结合资源层CPM的失效分布函数和有向边影响程度即可定义有向边ei→j的故障传播概率,即
P(ei→j)(t)=Fi(t)I(ei→j)
(15)
在确定故障传播路径L后,计算节点da故障沿路径L传递到db的故障路径传播概率,即

(16)
式中:∑P(ei→j)为模型G=[D,E]各有向边故障传播概率之和。
3.3 全电刹车系统故障传播强度模型
1) 故障传播强度模型建立
故障传播关键路径是最易导致故障迅速传播并造成严重后果的路径。在实际情况下,某些分支的故障传播概率不大,一旦故障通过该分支传播,故障的范围急剧扩大,造成大范围故障传播。考虑全电刹车系统故障传播结构模型的结构特征,根据文献[34],引入边缘介数,量化故障在网络中的流动频率,其值越大,有向边对节点控制效果越强,即越易引起故障的快速传播。边缘介数定义为

(17)
式中:ψxy表示任意节点dx和dy间的路径数;ψxy(ei→j)表示任意节点dx和dy间通过有向边ei→j的路径。
在此基础上,本文提出从全电刹车系统故障传播概率和边缘介数2个维度建立故障传播强度模型,给出计算公式为
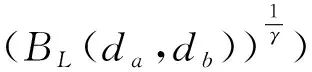
(18)
式中:PL(da,db)为故障路径传播概率;γ为故障传播路径L上的有向边个数;BL(da,db)为故障传播路径L上各有向边的边缘介数连乘积,定义为

(19)
2) 故障传播关键路径识别
故障传播关键路径由故障传播路径强度模型识别,式(18)中,QL(da,db)表示路径L故障传播强度,其值越大,路径L故障传播优先级越高。同理,可计算出G=[D,E]中所有路径故障传播强度,取值越大,故障传播能力越强。
各CPM节点的综合故障传播强度的计算,应综合考虑某一节点对全电刹车系统整个资源层的影响,即结合以某一节点作为故障传播源的故障传播结构模型,即
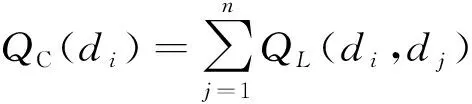
(20)
式中:QC(di)为节点di的综合故障传播强度,其值越大,表示节点di故障传播能力越强,其中i=1,2,…,n,j=1,2,…,n,n为全电刹车系统资源层CPM个数。
4 实例分析
4.1 全电刹车系统故障传播结构模型
结合DIMA平台下全电刹车系统架构,完成全电刹车系统功能层向系统资源层的映射,如表1 所示。

表1 全电刹车系统功能-资源映射关系
由于DIMA平台下全电刹车系统顶层任务仅为完成地面机轮减速,即T={t1},因此本文在此并未给出系统任务层与系统功能层的映射关系。在此给出全电刹车系统功能-资源层的映射关联矩阵Mfd为

(21)
根据上述功能-资源映射关联矩阵Mfd,不同资源层节点由同一系统功能所映射,产生直接耦合矩阵Cd,即

(22)
基于Floyd算法,输入直接耦合矩阵Cd计算故障传播路径阶数,得到故障传播间接耦合矩阵Cu和路由矩阵Cr为
(23)
(24)


图3 全电刹车系统资源层故障传播结构模型Fig.3 Resource layer fault propagation structure model of all-electric brake system
4.2 基于耦合关联分析的故障概率模型

(25)
式中:a、c为修正因子。可解得a=0.56、c=1。故由式(8)和间接耦合矩阵Cu可得失效严重程度矩阵:

结合上述矩阵SP,由式(9)可得耦合关联修正系数
ε=[0.778 7,0.865,0.733 7,0.606 2,0.588 8,0.823 7,0.588 8,0.402 5,0.647 5]
根据文献[6],设定各CPM服从指数分布,初始失效率为λ=2×10-5h-1,经耦合关联修正系数修正后,结合式(10),可得全电刹车系统资源层各CPM失效分布函数,如表2所示,相应函数曲线如图4所示。
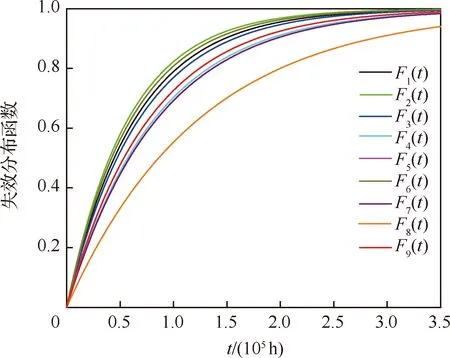
图4 全电刹车系统资源层CPM失效分布函数曲线Fig.4 Failure distribution function curve of CPMs for all-electric braking system resource layer
根据表2数据和式(12)可得,全电刹车系统资源层整体失效分布函数为

表2 全电刹车系统CPM失效分布函数
FZ(t)=1-e-1.207 1×10-4t
(26)
4.3 故障传播概率模型的建立
引入概率重要度与临界重要度,以量化资源层各CPM节点自身的故障影响程度,根据式(11)~式(13)以及表2,可得任意时刻全电刹车系统资源层CPM节点的概率重要度和临界重要度,各CPM的IP(di)(t)和IC(di)(t)函数曲线如图5、图6所示。

图5 全电刹车系统资源层CPM概率重要度曲线Fig.5 Probability importance function curves of CPMs for all-electric braking system resource layer

图6 全电刹车系统资源层CPM临界重要度曲线Fig.6 Critical importance function curves of CPMs for all-electric braking system resource layer
由图5和图6可知,当t≥2×105h时,各CPM概率重要度和临界重要度曲线均趋于稳定。结合图5、图6以及式(14)可得全电刹车系统资源层CPM间有向边影响度函数曲线,如图7所示。在此基础上,由式(15)可得图3(a)以CPM1为起点故障传播结构模型下各有向边的故障传播概率曲线,如图8所示。
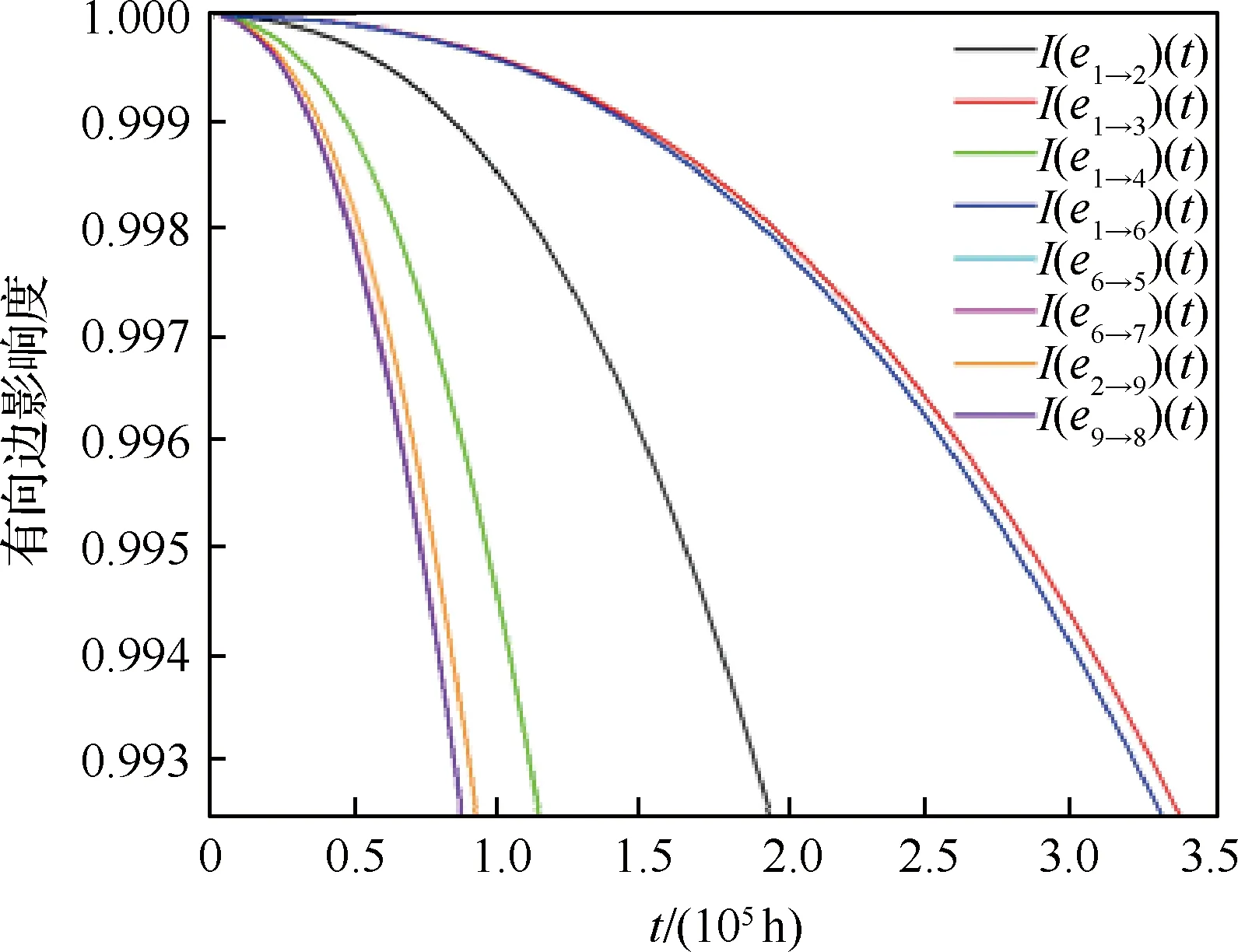
图7 全电刹车系统资源层CPM间有向边影响度曲线Fig.7 Directional edge influence function curves between CPMs for all-electric brake system resource layer
由图7可知,图3(a)所示以CPM1为起点故障传播结构模型中,各有向边影响程度均随时间t降低,其中I(e1→3)的取值最大,即图3(a)的8条有向边中,有向边e1→3的故障影响程度最大。且由图8可得,从t=2×105h之后,各有向边的故障传播概率曲线逐渐趋于稳定。
结合图8所示有向边故障传播概率曲线、图3(a) 所示的故障传播结构模型以及式(16),得出以CPM1为起点的故障路径传播概率,如图9所示。

图8 全电刹车系统资源层CPM有向边故障传播概率曲线Fig.8 Directed edge fault propagation probability curves of CPMs for all-electric brake system resource layer
由图9可知,在t=2×105h之前,图3(a)所示的以CPM1为起点的故障传播结构模型中,8条故障路径传播概率同样均趋于稳定,当t>2×105h时,PL(d1,d2)、PL(d1,d3)以及PL(d1,d6)路径的传播概率逐渐增大,PL(d1,d4)开始降低,考虑到各CPM概率重要度和临界重要度曲线均在t≥2×105h时趋于稳定,后续全局故障传播结构模型的故障传播关键路径的识别以及各节点的综合故障传播强度均以t=2×105h为例进行计算,相关数据如表3所示。
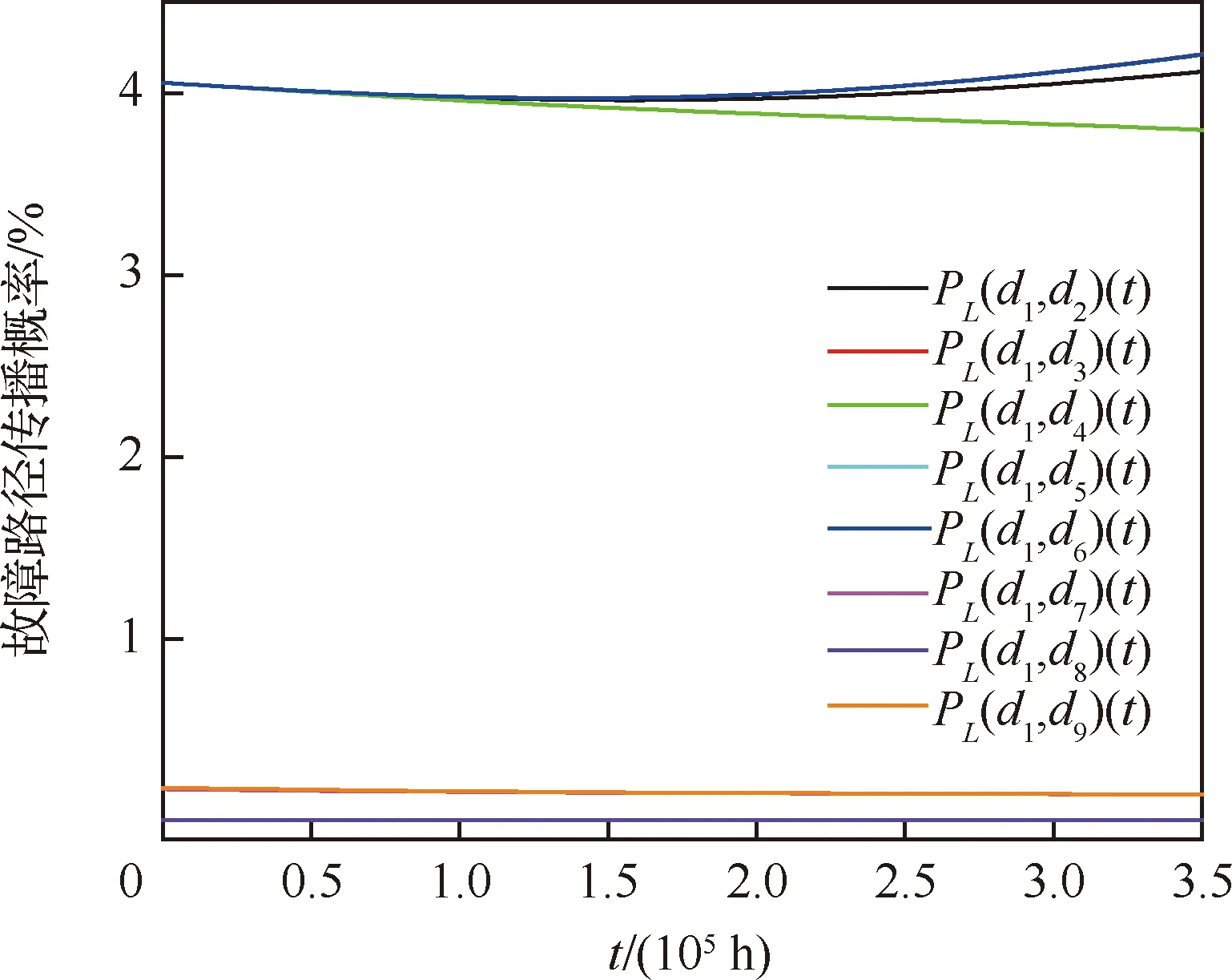
图9 以CPM1为起点的故障路径传播概率曲线Fig.9 Fault path propagation probability curves starting from CPM1

表3 t=2×105 h时以CPM1为起点的故障路径传播概率
4.4 故障传播强度模型的建立
从全电刹车系统故障传播概率和边缘介数两个维度建立故障传播强度模型,以识别不同故障传播结构模型下的故障传播的关键路径。
以图3所示全电刹车系统资源层故障传播结构模型为例,结合式(17),可得以CPM1为起点故障传播结构模型各有向边的边缘介数,如表4所示。
在表4基础上,根据式(18)、图9以及表3数据,可得图3(a)以CPM1为起点故障传播结构模型下的各路径故障传播强度,如图10所示。

表4 全电刹车系统资源层以CPM1为起点故障传播结构模型的边缘介数
根据图10(a)、10(b)以及10(e)可知,QL(d1,d2)、QL(d1,d3)以及QL(d1,d6)故障传播强度曲线变化相似,均是先降后升,且在t=1×105h时取最小值,其余路径的故障传播强度均随时间递减。同时由图10(i)可得,图3(a)以CPM1为起点故障传播结构模型中,路径L:d1→d2→d9→d8所对应的故障传播强度QL(d1,d8)最大,相比于图9中的PL(d1,d8)可知,各有向边的边缘介数对全电刹车系统资源层故障传播的影响不可忽略,边缘介数越大,说明其在故障传播中的作用越大。考虑到简化计算,后续故障传播强度的计算均以t=2×105h为例,同理可计算图3所示其余8个故障传播结构模型各传播路径在t=2×105h时的故障传播强度,各路径故障传播强度如下图11与表5所示。
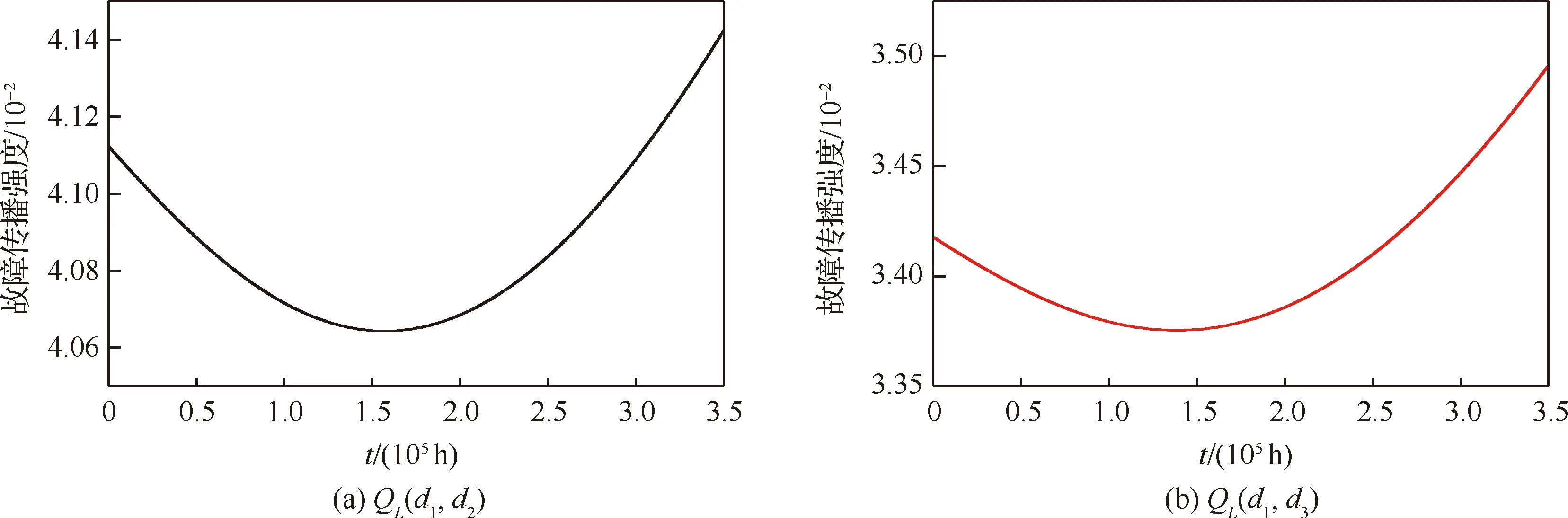
图10 以CPM1为起点传播路径故障传播强度曲线Fig.10 Fault propagation intensity curve starting from CPM1
由图11可得,当t=2×105h时,图3中全电刹车系统资源层故障传播结构模型72条传播路径中QL(d2,d9)取最大值,根据Pareto法则[35],在区分故障传播关键路径时,可以认为80%的事故源于20%的危险源,因此本文在将72条路径故障传播强度QL(di,dj)降序排序基础上,取前20%最大值定义为故障传播关键路径,如表6所示。
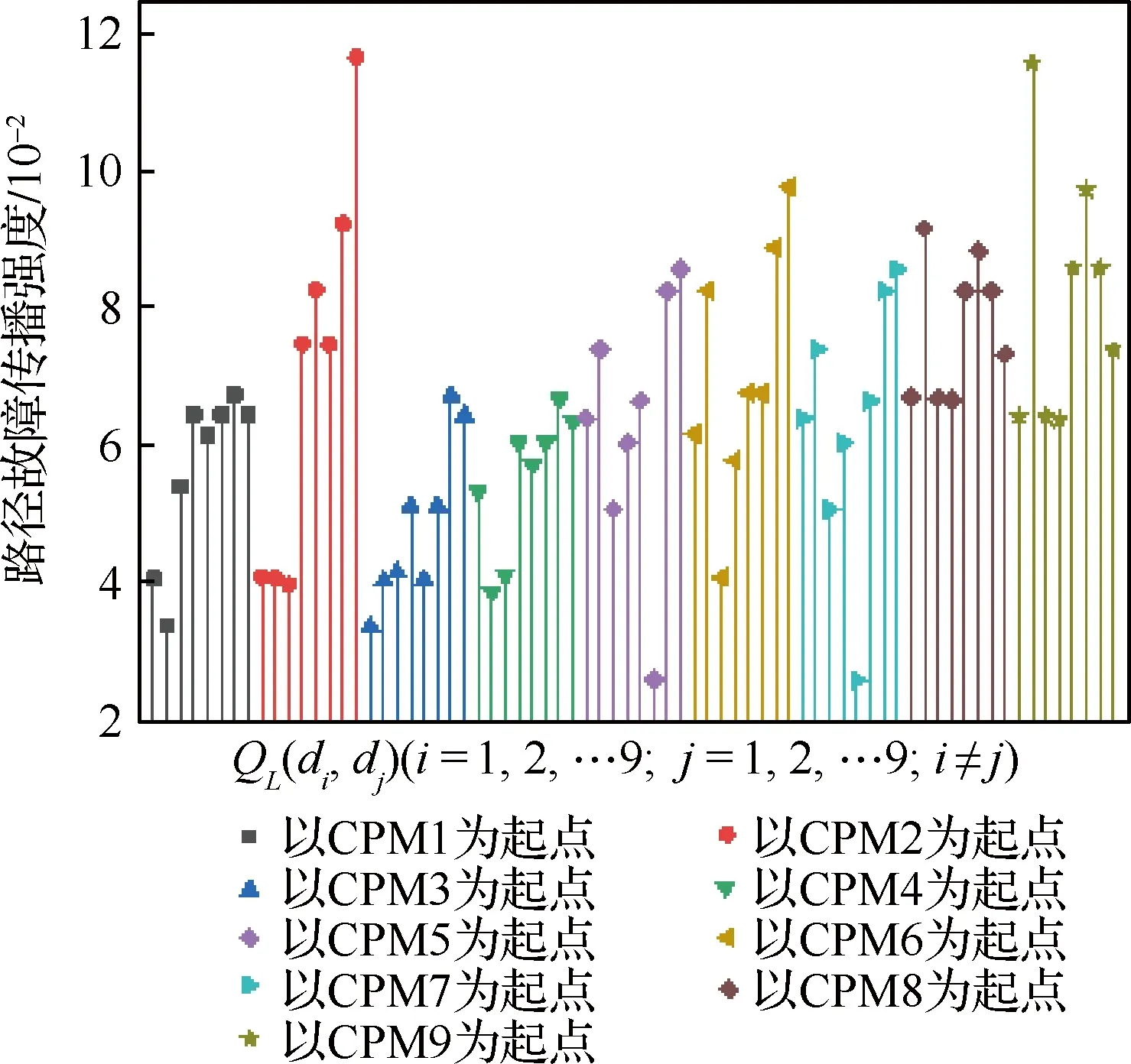
图11 t=2×105 h时各传播路径故障传播强度Fig.11 Fault propagation intensity of each propagation path when t=2×105 h
针对各CPM节点综合故障传播强度,以某单一节点di作为故障传播源,根据表5所示数据,结合式(20)可得t=2×105h时各节点综合故障传播强度,如表7所示。
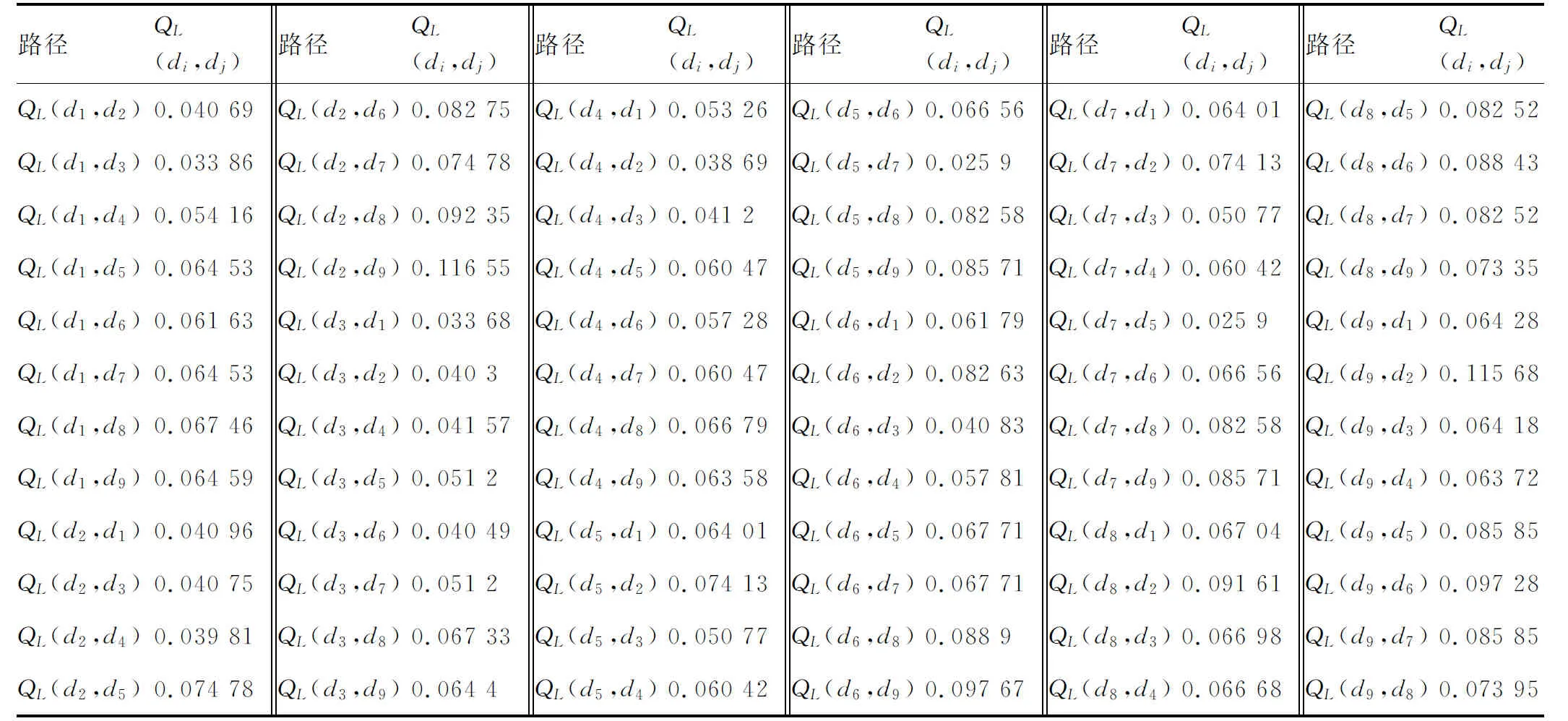
表5 t = 2×105h时各路径的故障传播强度Table 5 Fault propagation intensity of each path when t = 2×105h
根据表7可知,t=2×105h时全电刹车系统资源层9个CPM节点的综合故障传播强度依次为:CPM9>CPM8>CPM2>CPM6>CPM5≥CPM7>CPM1>CPM4>CPM3。在实际情况中,常规飞机全电刹车系统核心关键模块主要包括负责制动参数解算和刹车模式选择的刹车控制单元(Brake Control Unit,BCU)和防滑控制盒,上述模块的故障传播能力较低。根据表6可知,在本文所定义的故障传播关键路径中并未包含CPM1制动参数解算模块、CPM3防滑算法模块以及CPM4刹车模式选择模块,即在DIMA架构下全电刹车系统中,上述核心处理模块的故障传播能力相对较弱,且有利于动态重构的快速配置,同时尽可能提高上述模块的可靠性,以最小化对系统的影响,可见本文计算结果符合实际情况。与之相比CPM2刹车指令输出模块以及CPM9机轮速度显示等模块的故障传播能力较强,上述模块的不确定性较高,其失效对系统的影响较大。在实际系统设计过程中,在保证CPM可靠性的前提下,可考虑多模冗余配置,引入综合远程数据采集器单元(Integrated Remote Data Concentrator Unit,IRDCU)作为相应备份冗余模块,此单元可设置相应分区,驻留与CPM2对应的远程刹车指令输出软件,同时考虑刹车系统实时性需求,引入高速现场总线,实现与DIMA平台或传感器的数据通信。

表6 t=2×105 h时全电刹车系统资源层故障传播结构模型关键路径
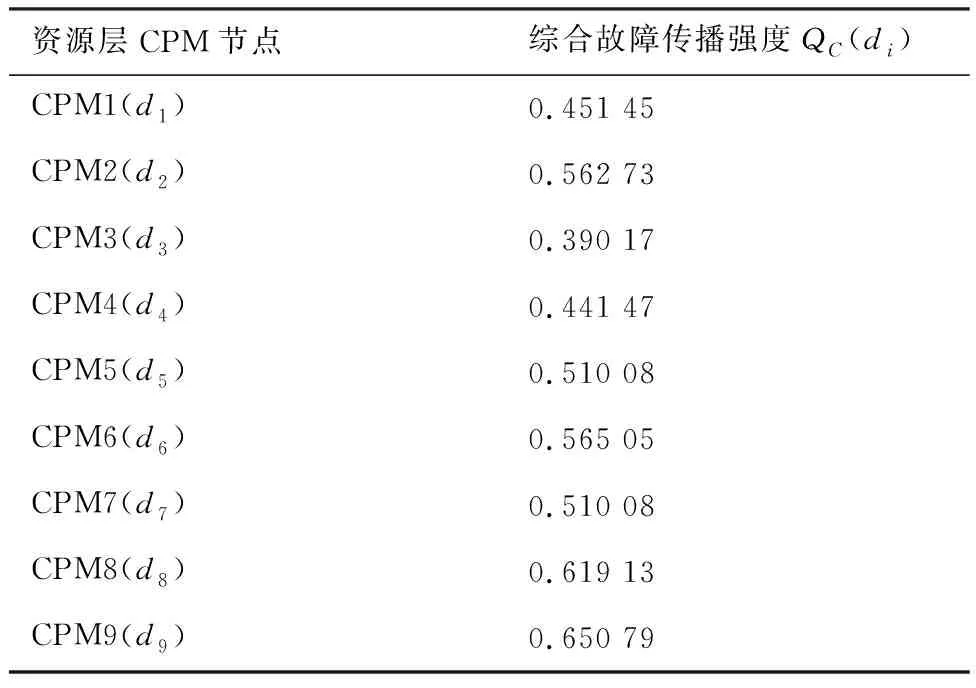
表7 t=2×105 h时各节点的综合故障传播强度
5 结 论
1) 本文结合DIMA架构下全电刹车系统架构特征,从系统任务层、功能层以及资源层构建了系统层次模型,针对资源层不同CPM间的高度耦合,开展了全电刹车系统资源层耦合关联分析,输出了系统直接耦合矩阵与间接耦合矩阵,在此基础上,结合失效严重程度矩阵和路由矩阵建立了基于耦合关联分析的故障概率模型和系统故障传播结构模型。
2) 在基于耦合关联分析的故障概率模型的基础上,引入了概率重要度、临界重要度以及耦合度函数,以量化各CPM节点自身和有向边的故障影响程度,建立了全电刹车系统故障传播概率模型,以输出各故障路径传播概率,结合系统的边缘介数,建立了全电刹车系统故障传播强度模型。
3) 通过DIMA架构下全电刹车系统实例,计算了各CPM节点的综合故障传播强度,给出了14条故障传播关键路径,验证了所提方法的合理性和正确性,可为后续DIMA架构下的飞机全电刹车设计提供参考。

