基于人工神经网络的可压缩湍流大涡模拟模型

谢晨月，王建春,*，万敏平，陈十一

1. 南方科技大学 工学院 力学与航空航天工程系， 深圳 518055

2. 南方科技大学 粤港澳数据驱动下的流体力学与工程应用联合实验室， 深圳 518055

大涡模拟方法适用于研究复杂湍流问题，比如航空航天、大气、海洋、能源、天体物理等领域中遇到的湍流问题[1-7]。湍流大尺度结构主导着动量、能量和热量的传输。受限于目前计算机的计算能力，无法使用直接数值模拟(DNS)方法获得高雷诺数湍流在各个尺度上的所有流场信息。大涡模拟方法主要通过使用较粗的网格求解湍流中的大尺度结构，同时构造近似的亚格子(SGS)模型表达小尺度结构对大尺度运动的影响[8-10]。在可压缩湍流中，热力学量和速度之间相互耦合，旋涡、声波、膨胀波以及激波之间存在着非线性作用[7-8,11-17]。可压缩湍流的速度脉动和温度脉动存在多尺度级串现象，相关研究有助于发展可压缩湍流的亚格子模型[16-17]。可压缩湍流的大涡模拟需要封闭动量方程和能量方程中出现的亚格子项，包括亚格子应力和亚格子热通量。国家数值风洞(NNW)工程自主研发了功能先进、种类齐全的国家空气动力数值模拟平台。在国家数值风洞工程框架下，发展适用于高雷诺数的高精度和高稳定性的可压缩湍流亚格子模型对航空、航天、能源等领域中的重大工程问题至关重要[18]。

滤波宽度Δ是建立亚格子模型的核心参数。特征尺度接近滤波宽度Δ的湍流结构对重构亚格子不封闭项起着重要的作用，比如变分多尺度Smagorinsky模型考虑到了这部分湍流结构的影响[19]。从湍流多尺度级串过程的空间局部性分析得知，特征尺度在Δ/2～2Δ之间的湍流结构对滤波宽度为Δ的亚格子动能流量起主要作用[20]，这给发展高精度亚格子模型提供了理论依据。

近年来，机器学习方法已经广泛应用在湍流建模问题中，包括雷诺平均方法(RANS)和大涡模拟方法两大类[21-52]，比如：嵌入不变性特征的人工神经网络RANS模型[21]、基于贝叶斯框架含物理约束的RANS模型[22]、基于全连接人工神经网络的亚格子模型[25]、基于数据驱动的反卷积亚格子模型[28,30,32]、基于循环神经网络和Mori-Zwanzig公式的时空亚格子模型[37]、基于不同空间位置上的流动结构的各类人工神经网络亚格子模型[28,35,38-46]、以及基于局部坐标系的人工神经网络雷诺平均模型[47]等。

最近，针对不可压缩湍流和弱可压缩湍流的大涡模拟，一类基于湍流的多尺度空间结构特性的高精度空间人工神经网络模型(SANN)被提出[41-43]。通过使用直接数值模拟的湍流数据训练之后，SANN模型能够精确地表达特征尺度在Δ/2～2Δ范围内的湍流结构和滤波宽度为Δ的各个亚格子项之间的高维度、非线性的映射关系，克服了传统建模方法在高维数据拟合方面的局限性。SANN模型和文献中已有的其他亚格子模型的一个重要区别是：该模型精确地表达了尺度在Δ/2～Δ范围内的湍流结构的作用，而之前的建模方法主要考虑尺度在Δ之上的流场结构。由于尺度在Δ/2～Δ范围内的湍流结构对滤波宽度为Δ的亚格子动能流量起重要作用[20]，传统模型无法精确地表示这一作用，因此在先验分析中的相对误差会很大。SANN模型弥补了这一缺点，从而能够在先验分析的精度上远远超过传统的大涡模拟模型[41-43]。另一方面，传统大涡模拟采用的网格尺度一般等于滤波尺度Δ，从而一直存在数值误差和亚格子模型误差之间相互影响的问题。在先验分析中具有很高精度的亚格子模型(例如：梯度模型)，由于数值误差的干扰，会有不稳定的现象，在实际大涡模拟中的计算结果误差比较大，比不上强耗散亚格子模型(例如：Smagorinsky模型)。大涡模拟采用尺度为Δ/2的密网格，从而能够有效地抑制数值误差的影响，并体现出亚格子模型的高精度特性。传统的强耗散亚格子模型由于在滤波尺度附近的耗散过大，超过了物理上的亚格子耗散，从而导致流场在小尺度上的动能偏小，而在较大尺度上的动能偏大，在流动结构上表现为旋涡结构偏大，在统计特征上表现为能谱会有一定的倾斜。SANN模型克服了这个问题，所预测的流场结构在各个尺度上都和滤波后的直接数值模拟结果很接近，所得能谱在各个波数上都几乎和滤波后的直接数值模拟结果重合[41-43]。

在本文中，SANN模型被用来开展强可压缩湍流的大涡模拟研究。训练SANN模型使用的直接数值模拟数据是网格分辨率为1 0243的可压缩均匀各向同性湍流[16-17]。SANN模型2个重要控制参数和湍流马赫数对模型预测精度的影响被系统地评估。通过先验和后验分析得到，SANN模型比动态Smagorinsky模型(DSM)、动态混合模型(DMM)等传统模型更精确，能更好地预测强可压缩湍流的统计性质和流场结构。

1 控制方程和数值方法

(1)

(2)

(3)

可压缩湍流的泰勒雷诺数Reλ和湍流马赫数Mat分别定义为[11-12]

(4)

(5)

柯尔莫哥洛夫尺度η和积分尺度LI分别定义为[11-12]

(6)

其中：ε=σijSij/(Reρ)为单位质量的耗散率；E(k)为单位质量的能谱，满足E(k)dk=(urms)2/2。

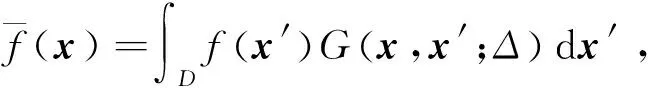
(7)

(8)

(9)

(10)

(11)

(12)

(13)

2 可压缩湍流的直接数值模拟数据

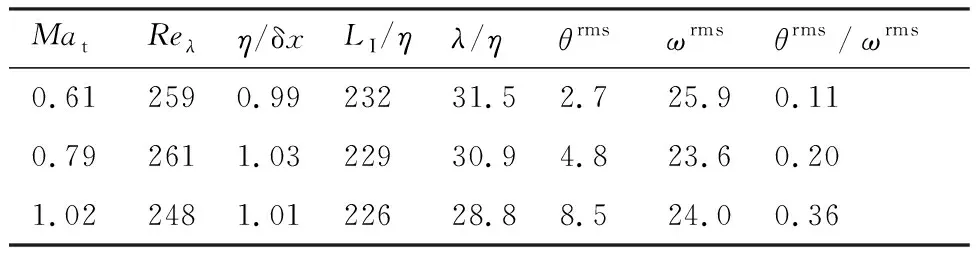
表1 网格规模为1 0243的可压缩各向同性湍流直接数值模拟的参数和统计量

本文采用盒式滤波器对物理量进行滤波，从而获得滤波后的物理量和亚格子应力τij和亚格子热通量Qj。一维的盒式滤波器定义为[16,56]

(14)

式中：滤波宽度Δ=nδx，本文采用的滤波宽度Δ=32δx。如图1所示，E(k)为动能能谱,滤波宽度位于惯性区，同时流场中有约10%的湍动能被滤掉。

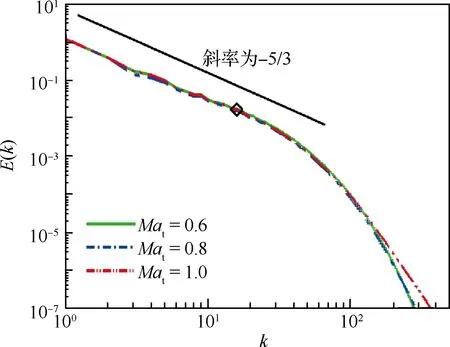
图1 可压缩湍流直接数值模拟数据的动能能谱(菱形表示滤波宽度为Δ/δx=32)Fig.1 Kinetic energy spectrum from direct numerical simulations of compressible turbulence (diamond represents filter width Δ/δx=32)

3 空间人工神经网络模型(SANN)

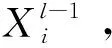
图2 人工神经网络结构示意图Fig.2 Schematic diagram of artificial neural network structure

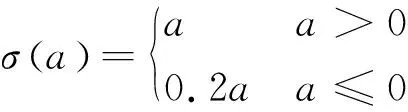
(15)

输出层的激活函数为线性函数σ(a)=a。人工神经网络的损失函数定义为(XO-τij)2或(XO-Qj)2。通过反向传播算法最小化损失函数[41-45]。

基于湍流能量传输的多尺度空间特性，特征尺度接近滤波宽度Δ的湍流结构对构造亚格子模型起着重要的作用[19-20,41-45,62-66]，SANN模型构建了滤波后的速度和温度梯度与亚格子不封闭项之间的非线性关系[41-45]。SANN模型有2个重要的控制参数：输入量的空间模板宽度Δs和滤波宽度Δ之比：Rs=Δs/Δ；滤波宽度Δ和空间模板的网格尺度Δg之比：Rg=Δ/Δg。SANN模型的输入参数为

(16)

q1,q2,q3∈{1,2,…,RsRg}

(17)

(18)

本文的训练数据集是从直接数值模拟的可压缩湍流数据中提取的包含15×643个点的空间子集，训练数据集分为2部分：70%数据为训练集，30%数据为测试集。SANN(Rs,Rg)模型的人工神经网络通过Adam算法迭代优化1 000次[67]，同时训练样本集大小(Batch size)为1 000。SANN(Rs,Rg)模型的交叉验证可以参考文献[41-45]。在本研究中，神经网络训练采用GPU核心，4个并行GPU核心(NVIDIA Tesla K80 GPU)同时训练SANN(Rs,Rg)网络。网络训练1 000次需要的GPU时间与Rs和Rg的关系如表2所示，随着Rs和Rg增加，输入层神经元数M增加，GPU计算时间相应地增加。

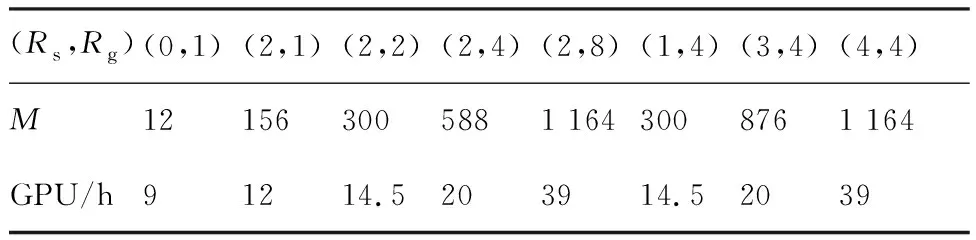
表2 SANN模型在不同的Rs和Rg情况下输入层参数个数M和训练1 000次需要的GPU时间

4 SANN模型的先验和后验分析

SANN模型应用在不可压缩湍流和弱可压缩湍流的大涡模拟中的结果可参考文献[41-45]。强可压缩湍流场中出现更多的激波结构，给大涡模拟计算带来了挑战。本文开展SANN模型在强可压缩湍流(Mat=0.6,0.8,1.0)中的先验分析和后验分析。在先验分析中，通过直接数值模拟数据计算的亚格子应力和亚格子热通量的相关系数和相对误差的变化反映了各类参数Rs、Rg和Mat对SANN模型预测精度的影响。在后验测试中，通过和传统的隐式大涡模拟(ILES)、动态Smagorinsky模型(DSM)、动态混合模型(DMM)进行比较， SANN模型能够高精度地预测强可压缩湍流的能谱、速度结构函数、速度散度概率密度分布函数和瞬态流场结构。

4.1 先验测试

SANN(Rs,Rg)模型预测的亚格子不封闭项Hmodel与真实亚格子不封闭项H的相关系数C(H)和相对误差Er(H)分别为

C(H)=

(19)

(20)

3种传统的亚格子模型分别为[68-71]

(21)

(22)

(23)

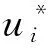
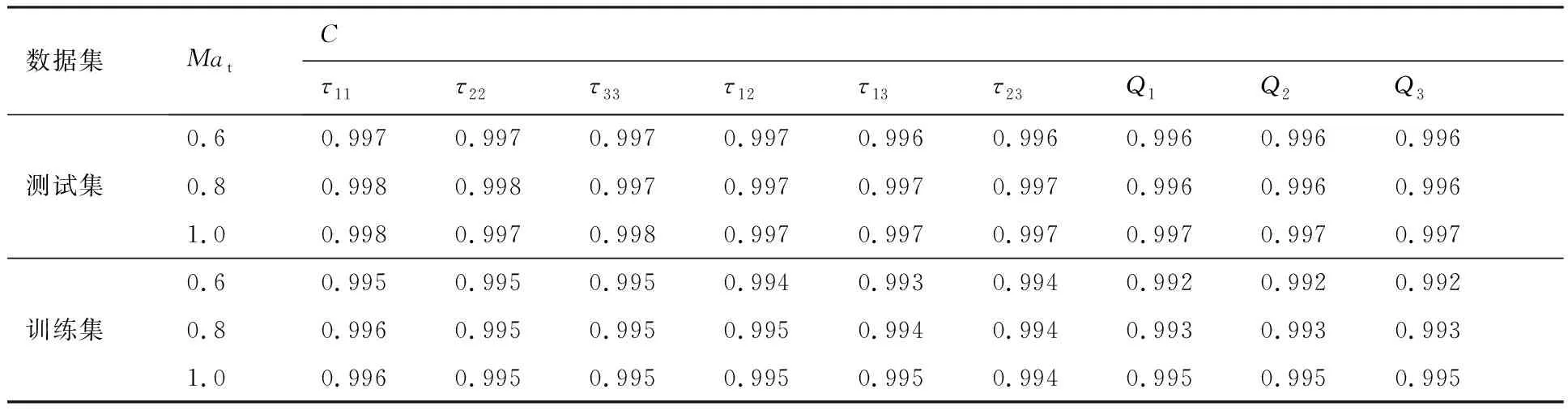
表3 SANN(2,1)模型在训练集和测试集上预测τ11,τ22,τ33,τ12,τ13,τ23,Q1,Q2,Q3的相关系数

表4 SANN(2,1)模型在训练集和测试集上预测τ11,τ22,τ33,τ12,τ13,τ23,Q1,Q2,Q3的相对误差

表5 不同亚格子模型预测τ11的相关系数和相对误差(Mat=1.0，Rs=2, Rg=1)

表6 不同亚格子模型预测τ12的相关系数和相对误差(Mat=1.0, Rs=2, Rg=1)Table 6 Correlation coefficient and relative error of τ12 for different SGS models (Mat=1.0, Rs=2, Rg=1)

表7 不同亚格子模型预测Q1的相关系数和相对误差 (Mat=1.0, Rs=2, Rg=1)Table 7 Correlation coefficient and relative error of Q1 for different models (Mat=1.0, Rs=2, Rg=1)

图3展示了在测试集上不同参数Rg和Mat对SANN(Rs,Rg)模型预测亚格子应力分量τ11的影响，其中Rs=2。VG1梯度模型预测的相关系数达到0.92，当Rg≥1时，SANN模型预测的相关系数超过0.99同时相对误差小于0.1。随着Rg增加，SANN模型预测的亚格子不封闭项与滤波后的直接数值模拟结果的相关系数增大，相对误差减小。特别地，湍流马赫数Mat对SANN(Rs,Rg)模型预测的结果影响不大。

图3 不同亚格子模型预测的不同Mat下τ11的相关系数和相对误差Fig.3 Correlation coefficient and relative error of τ11for different SGS models at different Mat

图4 或对τ11的贡献(Mat=1.0) to τ11 (Mat=1.0)

上述先验结果表明：在湍流马赫数为Mat=0.6,0.8,1.0情况下的高可压缩湍流中，相比传统的亚格子模型(DSM，DMM，VG1，VG1m，AD4)，SANN(Rs,Rg)模型预测的亚格子应力和亚格子热通量更接近滤波后的直接数值模拟结果：相关系数更高，相对误差更小。

4.2 后验测试

动态Smagorinsky模型使用了涡黏假设，能够对湍流的动能产生耗散作用，在统计平均意义上和湍流能量从大尺度转移到小尺度的物理级串过程类似[1,8,56,72]。对于可压缩湍流的大涡模拟，基于涡黏假设，亚格子应力和亚格子热通量分别近似为[41-45]

(24)

(25)

(26)

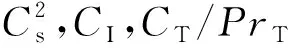
(27)

(28)

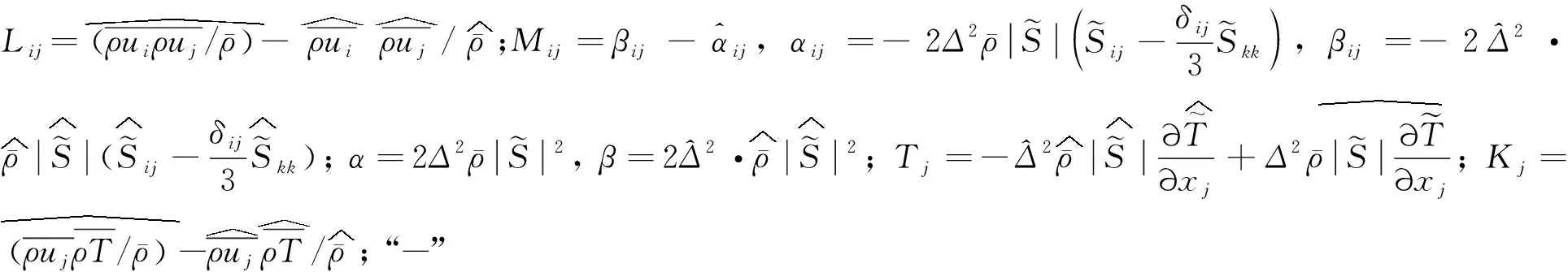
DMM由尺度相似项和涡黏耗散项组成[38,68-69,74]。对于可压缩湍流的大涡模拟，DMM的基本形式为[41-45]

(29)

(30)

(31)

(32)

(33)

同理，亚格子热通量Qj可以表述为

(34)

(35)

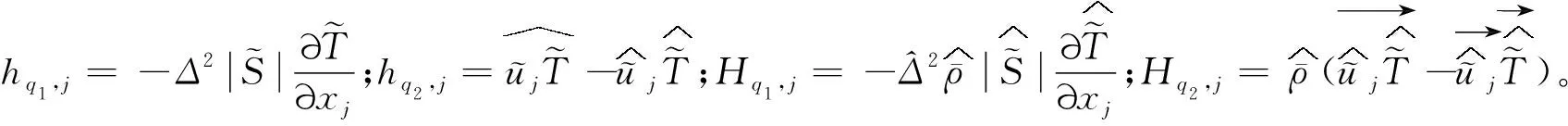
(36)

(37)

SANN(2,1)模型和传统模型预测的动能能谱和温度谱ET(k)如图5～图6所示。亚格子模型预测的能谱误差随着波数增加而变大。对于不加任何亚格子模型的情况，即No-model模型或隐式大涡模拟(ILES)，由于耗散不足，所预测的能谱高于滤波后的直接数值模拟结果(fDNS)；DSM和DMM模型在低波数k≤10的情况下出现能量聚集，同时在高波数耗散过大。SANN(2,1)模型预测的能谱更接近滤波后的直接数值模拟结果(fDNS)，几乎与fDNS的结果重合。

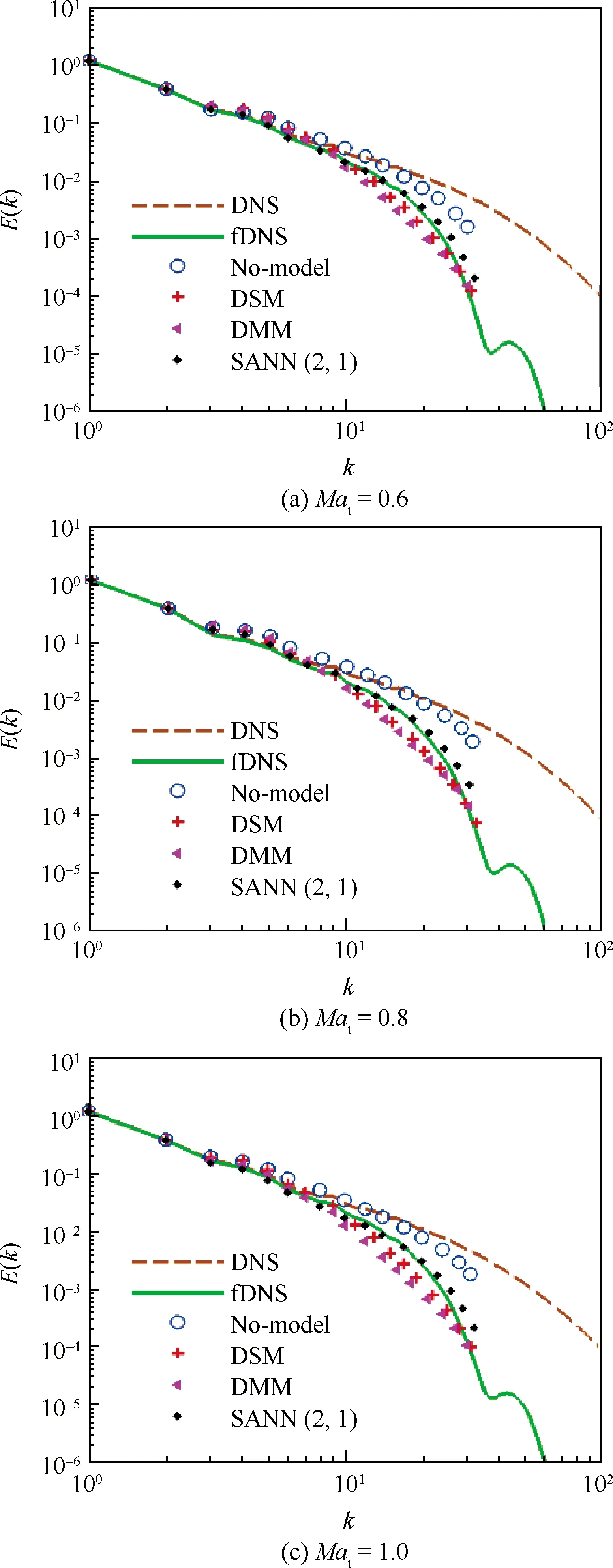
图5 不同模型预测的动能能谱(Reλ≈250)Fig.5 Kinetic energy spectrum predicted by different models (Reλ≈250)

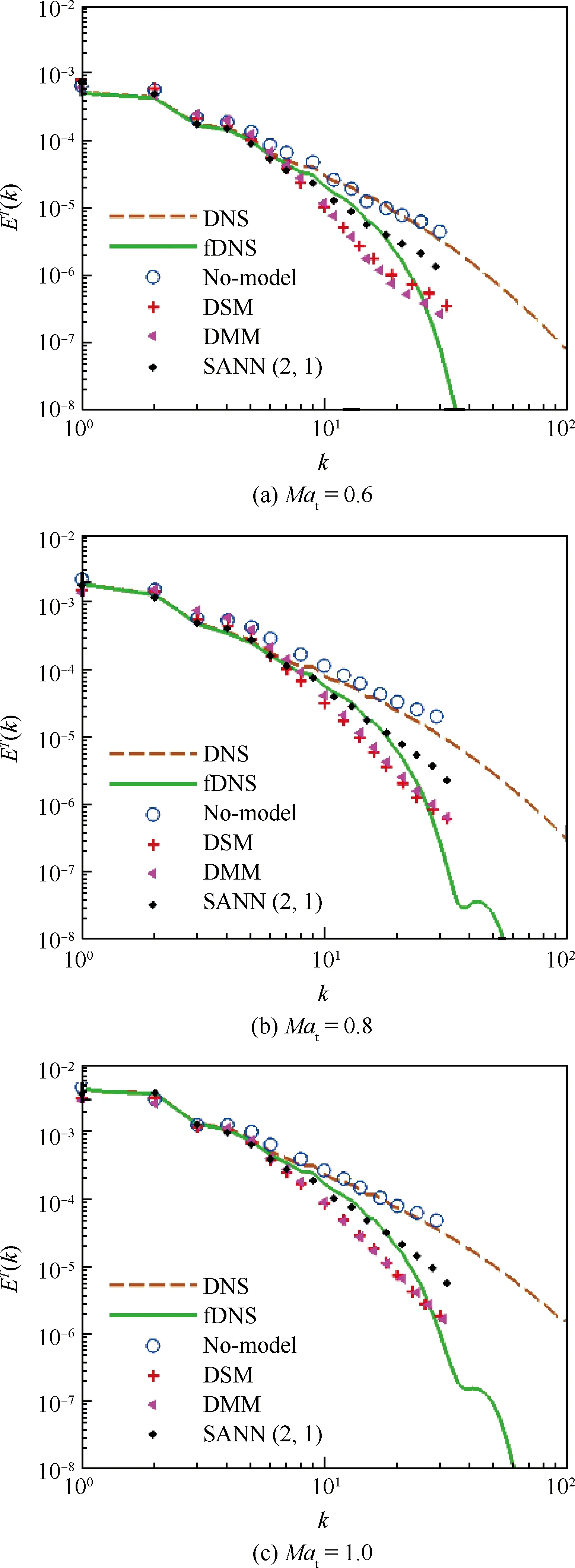
图6 不同模型预测的温度谱 (Reλ≈250)Fig.6 Temperature spectrum predicted by different models (Reλ≈250)

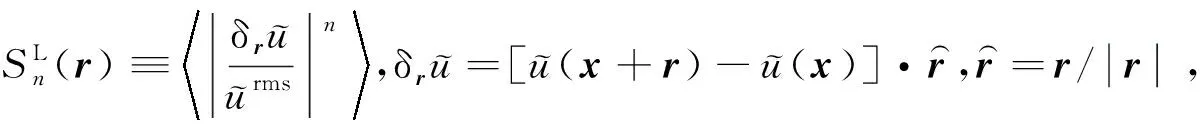
图7 Mat=1.0和Reλ≈250情况下的速度结构函数Fig.7 Structure functions of velocity at Mat=1.0 and Reλ≈250

图8 不同模型预测的归一化速度散度的概率密度函数(Reλ≈250)Fig.8 PDFs of normalized velocity divergence predicted by different models (Reλ≈250)

此外，本文评估了不同亚格子模型预测瞬态流场结构的表现。以滤波后的直接数值模拟流场的瞬态数据作为初始条件，使用DSM、DMM和SANN(2,1)模型开展可压缩湍流的大涡模拟。各类大涡模拟模型所预测的归一化速度散度云图如图9所示。不同模型均能预测出大尺度激波结构，SANN(2,1)模型比DSM和DMM模型重构出更多的小尺度结构，更接近滤波后的直接数值模拟结果。综上所述，SANN(2,1)模型可以高精度地预测不同湍流马赫数情况下的强可压缩湍流的统计特性和瞬态空间结构，在预测效果上优于传统的DSM和DMM模型。

图9 Mat=1.0和t/τ=3.21 (τ≡LI/urms为大涡翻转时间) 情况下的归一化速度散度云图Fig.9 Contours of normalized velocity divergence at Mat=1.0 and t/τ=3.21 (τ≡LI/urms is large-eddy turnover time)

5 结 论

本文采用空间人工神经网络模型SANN(Rs,Rg)对湍流马赫数为0.6、0.8、1.0情况下的强可压缩湍流开展了大涡模拟研究，分析了不同的参数Rs、Rg和Mat对SANN(Rs,Rg)模型预测亚格子应力和亚格子热通量的影响，并在先验分析和后验分析中，测试了SANN(Rs,Rg)模型在强可压缩湍流中重构流场的统计性质和瞬态结构的精确度，结果表明：

1) 与传统的梯度模型VG1、待定系数的梯度模型VG1m以及近似反卷积模型AD4相比， 空间人工神经网络模型SANN(Rs,Rg)在高湍流马赫数情况下的先验预测精度更高，相关系数达到0.995，相对误差小于11%。SANN(Rs,Rg)能够高精度地重构出亚格子应力、亚格子热通量与滤波后速度梯度之间的高维非线性映射关系。

综上所述，空间人工神经网络(SANN)模型可以精确地重构出强可压缩湍流的亚格子应力和亚格子热通量，并在大涡模拟中能够精确地预测湍流场的统计性质和空间结构。空间人工神经网络模型的主要优势是充分利用了人工神经网络建立高维度、强非线性映射关系的能力，并充分体现了湍流的多尺度结构对亚格子项的作用，因此具有非常高的精度，可以为发展其他大涡模拟模型提供精度上的参考标准。另一方面，空间人工神经网络模型的学习过程是一个黑箱过程，虽然输入物理量的选取保证了伽利略不变性，但该模型无法保证所预测的亚格子应力满足严格的对称性和可实现性等条件。为了优化人工神经网络模型，关于亚格子项的更多的数学结构和先验知识将被引入到模型中，使得新的模型具备对称性、可实现性和伽利略不变性等性质[45]。为了进一步发展高效率、高精度、适用范围广的人工神经网络亚格子模型，不仅需要进一步研究人工神经网络模型的可解释性，同时还需要将更多的湍流物理特性融入人工神经网络框架，比如：湍流的统计特性与相干结构之间的关系，涡结构与激波结构之间的相互作用，速度场与热力学参数之间的非线性耦合以及亚格子不封闭项的时空特征等。

本文对湍流马赫数分别为0.6、0.8、1.0的可压缩湍流开展了大涡模拟研究。此外，文献[41-43]讨论了空间人工神经网络模型在不可压缩湍流和弱可压缩湍流(湍流马赫数为0.4)中的应用。因此，这类模型在不可压缩湍流和湍流马赫数1.0以下的可压缩湍流中均具有很好的预测能力。这些结果表明空间人工神经网络模型具有较为广泛的适用范围。另一方面，航空航天领域面临的湍流问题会涉及各类复杂的条件，包括：复杂的流动结构、复杂的几何外形、湍流燃烧过程、高温气体效应等。

当前空间人工神经网络模型主要针对均匀各向同性湍流展开，只能保证适用于充分发展的湍流区域中，具有一定的局限性。接下来壁面效应、湍流燃烧以及高温气体效应等因素的影响将被加入到空间人工神经网络模型中。比如，文献[47]用机器学习方法对周期山状流进行了雷诺应力建模。国家数值风洞工程致力于自主研发功能先进的CFD软件系统。结合湍流的多尺度性质和人工神经网络方法的高精度大涡模拟方法有潜力适用于各类工程湍流问题，将其发展成为NNW自主研发软件系统的一个模块，可为解决航空航天相关的湍流问题提供支撑。