基于有限元的车体材料301L-DLT冷轧不锈钢断裂分析

卢 翀，曹 玉，黄 健，高福来

（1. 中国铁道科学研究院集团有限公司 标准计量研究所，北京 100081；2. 中铁检验认证中心有限公司，北京 100015）

轨道车辆主要在信号系统的引导下运行，发生事故的概率要远远低于其他交通运输工具，但是在地震及道岔、线路和车辆故障等偶然因素的作用下，仍然存在发生列车脱轨、碰撞等事故的可能性［1］。轨道车辆通常采用多编组连挂的方式运营，在偶然因素的作用下，列车脱轨后，各节车厢之间将会产生一系列的相互碰撞，造成车辆爬车、倾覆、挤压等破坏，带来巨大的人员伤亡和财产损失［2］。车体材料的断裂性能是列车脱轨后为乘客提供最大限度安全保护的基础。

采用有限元方法进行列车碰撞后的被动安全研究可以有效降低研发成本、缩短研发周期［3］，但是由于当前有限元模型简化了车体材料在极端条件下的断裂行为，导致有限元计算的结果与实际结果存在一定的差异［4］。因此，建立不锈钢在复杂应力状态下的断裂模型，是准确模拟轨道车辆车体碰撞的基础。

本文设计了3 种不同缺口尺寸的试样，分别进行拉伸断裂试验，基于试验结果应用G-T-N 断裂理论与J-C断裂理论，建立301L-DLT 冷轧不锈钢的断裂模型，再采用有限元方法，分析车体材料301L-DLT奥氏体冷轧不锈钢在不同应力状态下的损伤及断裂机制，探索韧性断裂与应力三轴度之间的关系，为使用有限元方法准确模拟车体碰撞断裂的过程提供了基础。

1 301L-DLT 冷轧不锈钢材料特性和拉伸断裂试验方案

1.1 材料特性

试验所用材料为轨道车辆车体材料301L-DLT冷轧不锈钢。该材料中主要化学元素的质量分数见表1。我国的301L-DLT 冷轧不锈钢目前参考日本JIS G 4305 冷轧不锈钢技术标准，屈服强度高达350 MPa以上［5］。

表1 301L-DLT冷轧不锈钢主要化学元素质量分数 %

1.2 拉伸断裂试验方案

为了研究在受到单轴拉伸载荷时，材料的应力三轴度与缺口尺寸的变化关系，设计了3种不同尺寸缺口的试样，即无缺口试样及2 和4 mm 缺口试样［6］。试验样件均由1.5 mm 厚的301L-DLT 冷轧不锈钢板材通过电火花线切割机加工而成，3 种试样的几何尺寸如图1所示。

图1 试样几何尺寸（单位：mm）

试验参照GB/T 228—2010《金属材料拉伸试验第1 部分：室温试验方法》，基于WDW-10 000 W 万能试验机进行，如图2所示。试验在准静态条件下进行，因此将拉伸速度设置为0.5 mm·min-1［6］。试样的位移通过标距长度为20 mm 的YYU50-25电子引伸计进行采集。为了保证试验的可靠性，每种试样重复进行3次。

图2 拉伸断裂试验

2 拉伸断裂试验结果与断口形貌

2.1 拉伸断裂试验结果

通过无缺口及2 和4 mm 缺口试样的拉伸断裂试验，测量得到载荷-位移曲线如图3所示。3次重复试验测量得到的载荷-位移曲线基本一致，试验的最大误差小于5%，表明试验的重复性较好。

从图3可以看出：3种试样的载荷-位移曲线在屈服后出现差异，无缺口及2 和4 mm 缺口试样拉伸试验的最大载荷分别为4.40，4.88 和5.01 kN，最大位移分别为12.80，1.61 和1.38 mm；表明缺口尺寸对301L-DLT 冷轧不锈钢材料断裂时的最大位移影响非常明显。这种相同材料拉伸断裂性能的差异性，主要是由于不锈钢薄板材料在单向拉伸断裂前出现材料塑性应变集中引起的失稳颈缩。对薄板试样进行单向拉伸时，在拉力作用下，一方面面积缩减，另一方面应变硬化效应增加，当材料应变硬化效应的增量足以补偿承载面积的缩减时，拉伸变形可以稳定地进行下去，当二者恰好相等时，拉伸变形处于临界状态，失稳首先发生在材料承载能力最为薄弱的位置，从而出现缩颈。不同尺寸的缺口导致承载能力最为薄弱的位置发生变化，进而影响到材料最终发生的断裂行为。

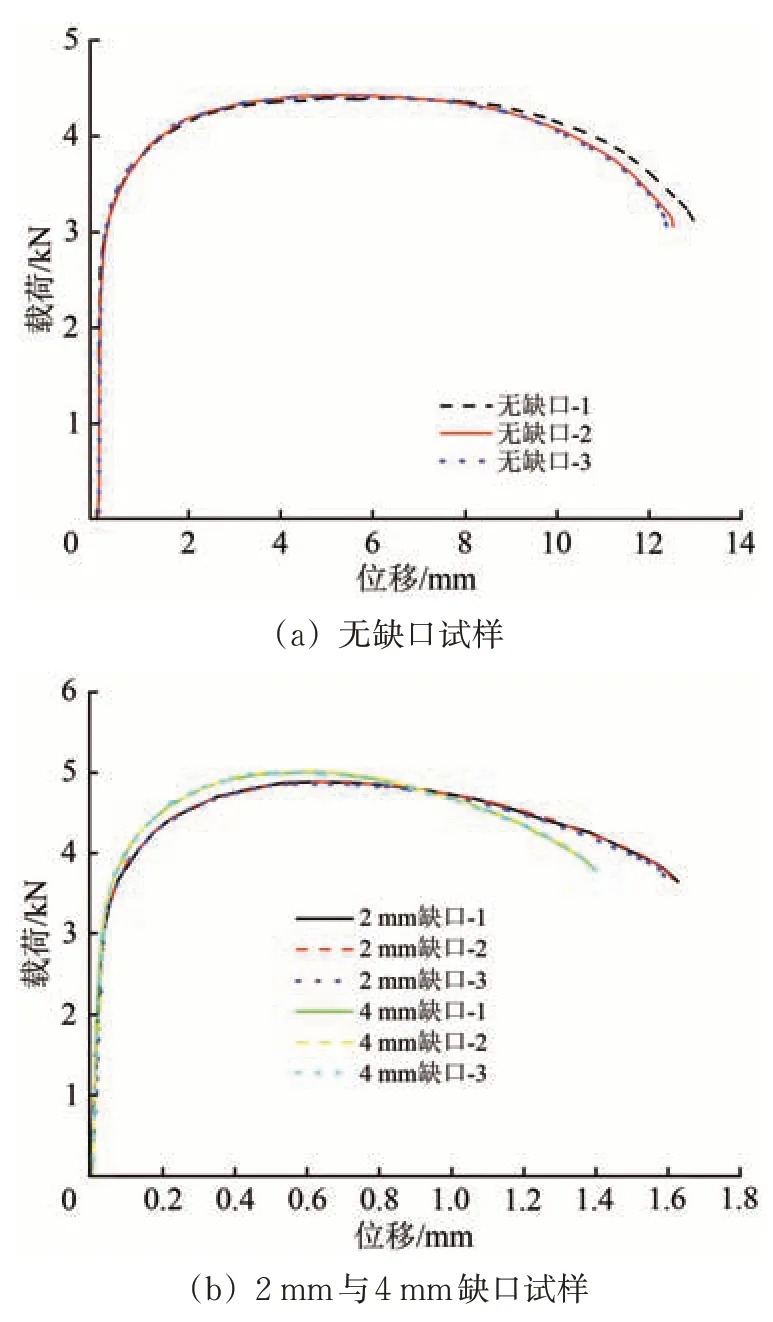
图3 试样拉伸断裂试验的载荷-位移曲线

2.2 断口形貌

采用Zeiss—SIGMA HD 型场发射扫描电子显微镜分别对3种试样的断口进行观察，通过10倍放大效果观察材料的断口面积，通过200 倍和1 000倍放大观察断口的微观形貌特征，分别如图4—图6所示。

图4 试样断口处的显微照片（10倍）

图5 试样断口处的显微照片（200倍）

从图4 可以看出：断口的宏观形貌如“杯锥状”；虽然不同试样在拉伸前缺口处的宽度和厚度均为5.0 和1.5 mm，但是拉伸后由于失稳颈缩导致的厚度和宽度的变化并不相同，从而引起断裂应变也发生变化。

不同试样的真实断裂应变εf为

式中：A0为试样缺口处的原始横截面积；Af为断口在拉伸应力方向上的投影面积。

通过式（1）计算得到无缺口及2和4 mm 缺口试样的断裂应变分别为1.41，0.78和0.81。

从图5 和图6 可以看出：断口中心布满韧窝，断裂面为典型的韧窝断裂［6］，韧窝的尺寸为2～5 μm，在部分韧窝中心出现韧性夹杂物和第二相微粒，这是高应力三轴度断裂的典型特征；这也反映了在该应力状态下，301L-DLT冷轧不锈钢的韧性断裂机制为在加载过程中孔洞在夹杂物和第二相微粒周围不断萌生、扩展、聚合，最终引起了宏观裂纹。

图6 试样断口处的显微照片（1 000倍）

3 拉伸断裂试验有限元建模

采用有限元软件LS-DNYA，分别建立无缺口及2 和4 mm 缺口试样的有限元模型，如图7 所示。建模时，有限模型采用三维实体全积分单元模拟，在中心应力集中区域的单元尺寸划分较细、为0.5 mm，其余区域为1 mm，无缺口及2 和4 mm 缺口试样分别包含10 488，13 716 和11 436 个实体单元。在有限元模拟中采用了与试验相同的加载方式及边界条件［6］。

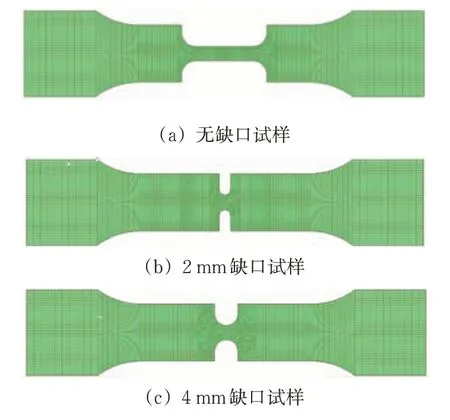
图7 3种试样的有限元模型

使用应力三轴度作为描述断裂应力状态的指标时，拉伸断裂的应力三轴度η需要通过有限元分析测量校正。应力三轴度的定义为

式中：σM为von Mise应力；σH为平均静水压力。

仿真计算得到3 种不同试样在拉伸断裂试验中的应力三轴度分布情况如图8 所示。从图8 可以看出，3 种试样的应力三轴度分布在0.33～0.81 之间，不均匀的应力三轴度分布表明在拉伸断裂过程中发生了明显的失稳颈缩。

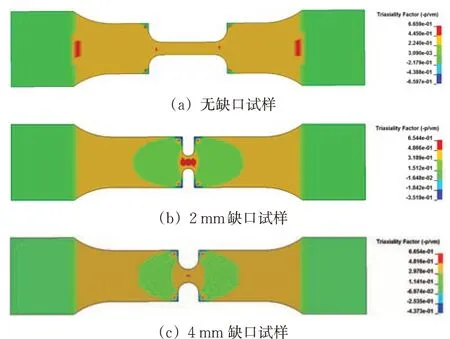
图8 拉伸断裂试验的应力三轴度分布云图

通过有限元计算得到3 种试样拉伸断裂试验断口中心位置的应力三轴度-塑性应变曲线如图9 所示。3 种试样拉伸断裂试验的平均应力三轴度及断裂塑性应变见表2。

根据表2 和图9 可以看出：3 种试样的平均应力三轴度较为接近，在0.61～0.67 之间；断裂应变的差异较大，其中无缺口试样的断裂应变最大，为1.41。

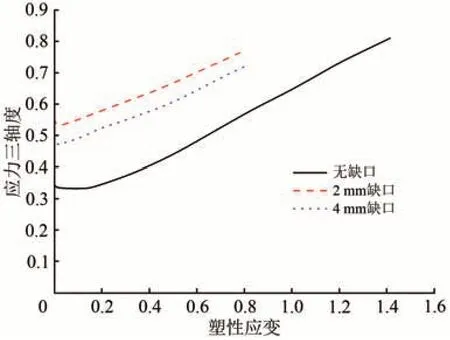
图9 拉伸试验断口中心位置的应力三轴度-塑性应变曲线

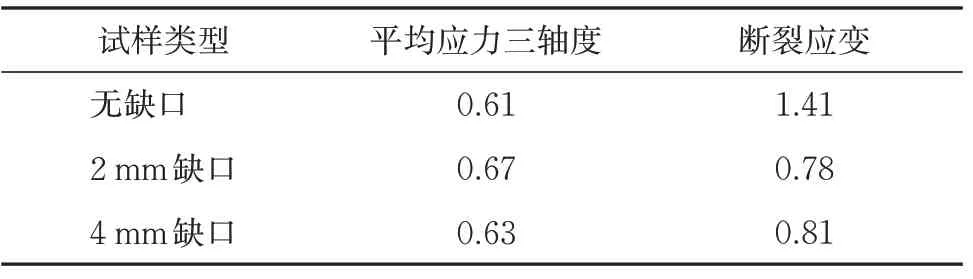
表2 3种试样拉伸试验断口中心位置的平均应力三轴度及断裂应变

4 基于J-C 和G-T-N 断裂理论数值模拟与试验结果对比

4.1 基于J-C断裂理论的数值模拟

上述试验表明：301L-DLT冷轧不锈钢的韧性断裂应变明显受到应力状态的影响，在试验中试样的应力状态在宏观和微观上都表现出明显的韧窝断裂特征，但是由于试样缺口尺寸的不同，导致塑性失稳和缩颈的程度发生明显变化，最终在数值上表现为断裂应变的不同。基于韧性断裂的演化过程，Johnson-Cook等［7］提出的韧性断裂理论为

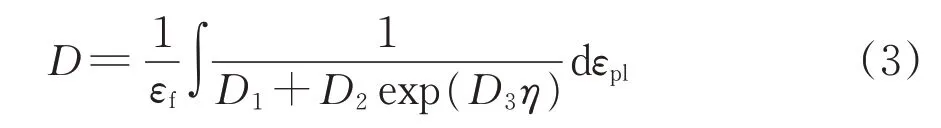
式中：D为间接代表微孔洞的体积分数（微孔损伤变量），D=1时发生断裂；εpl为等效应变；D1，D2和D3为材料常数，为与塑性变形中产生的微损伤有关的参数。

将表2 的数据代入式（3），得到拉伸断裂试验断裂应变在应力三轴度空间的分布如图10所示。

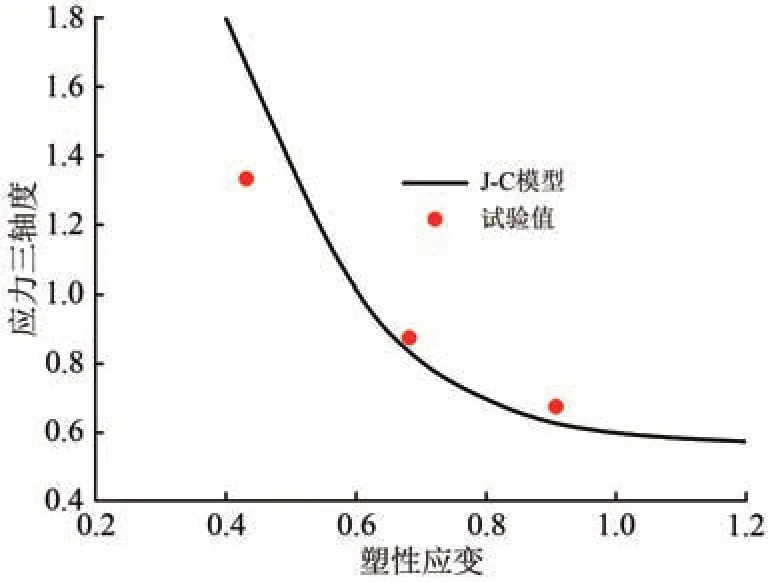
图10 拉伸断裂试验断裂应变与应力三轴度关系

通过数值拟合得到301L-DLT 冷轧不锈钢基于J-C断裂理论的数值模型为

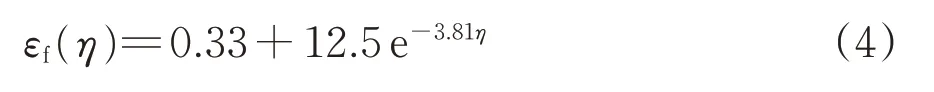
4.2 基于G-T-N断裂理论的数值模拟

Gurson［8］在材料的屈服函数中考虑了损伤和静水压力的影响，被广泛用于分析韧性断裂过程。Tvergaard［9-10］和Needleman［11］对Gurson 模型进行了修正，通过引入等效孔洞体积分数f*和模型修正参数q1，q2，提高了原始Gurson模型的预测精度，其公式表达［11］为

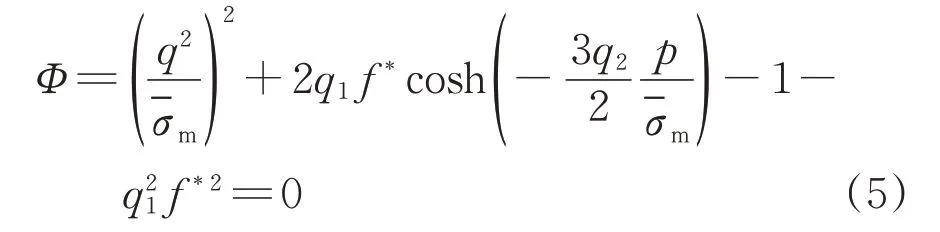
式中：Φ为剪切效应的屈服函数；p为静水压力；q为等效应力；为基体材料的流动应力。

孔洞聚合发生在材料内部的孔洞体积分数f达到聚合准则所确定的临界值时，即在损伤模型中f可通过f*代替，为

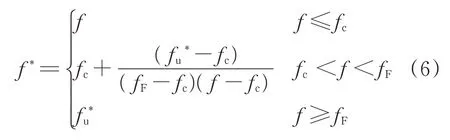
其中，

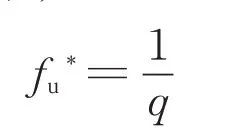
式中：fu*为应力为零时的临界孔洞体积分数；fF为基体断裂的临界孔洞体积分数；fc为孔洞发生聚合时的临界孔洞体积分数。

孔洞聚合发生前，可以通过现有孔洞的长大参数和新孔洞的萌生参数表示体积分数的变化［12］，即

其中，

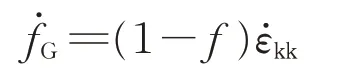
式中：ε˙kk为材料的体积变化率。

基体粒子在界面处的断裂或剥离是导致新孔洞萌生的主要原因，可通过式（8）定义应变控制的孔洞萌生准则［13］。

式中：A为萌生强度；εˉ˙p为基体等效塑性应变。

式（8）中，萌生强度为基体等效塑性应变εˉ˙p的函数，Chu［14］和Needleman［15］在研究中提出连续型萌生模型服从正态分布，即

式中：SN为正态分布的标准差；εN为孔洞萌生时的平均等效塑性应变；fN为孔洞体积分数形核部分的极限值。

该模型中包括11 个材料参数，即E（弹性模量），σ0（屈服极限），Et（硬化模量），q1，q2，fG（原有孔洞生长的体积分数），fc（孔洞发生聚合时的临界孔洞体积分数），fF（基体断裂的临界孔洞体积分数），fN（孔洞体积分数中形核部分的极限值），εN和SN。Tvergaard［8-9］提出，在q1=1.5，q2=1 时，计算值与试验值的吻合度最高；εN和SN分别取值0.3 和0.1；根据图3（a）无缺口试样的载荷-位移曲线得到301L-DLT 冷轧不锈钢的E、σ0和Et。fG、fc、fF、fN这几个参数决定了材料的损伤和失效，无法直接测得［16］，可以结合准静态下3种试样的拉伸断裂试验数据并应用优化算法计算得到，优化分析过程如图11所示。

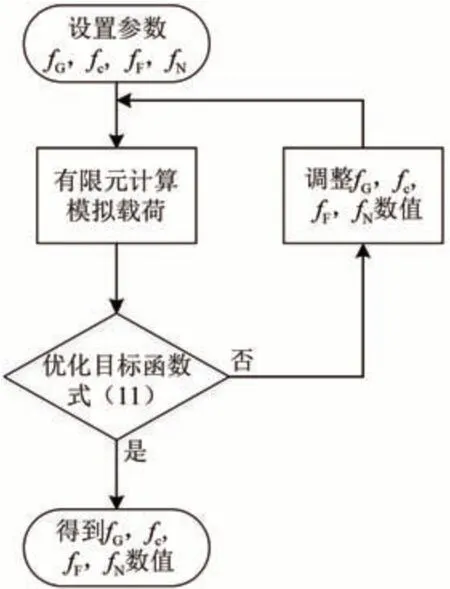
图11 G-T-N断裂理论参数优化流程图

在计算过程中首先需要输入fG，fc，fF和fN这几个参数初始值，使用有限元计算模拟得到的载荷，通过使用优化目标函数即式（11）［17］，将模拟载荷与试验测得的载荷F进行比价，即

式中：TOL为优化前给定的阈值；k为当前的载荷步；n为载荷步的总步数。

通过式（11），所构成的标准差满足给定的收敛条件。采用连续响应面法来进行参数的优化［18］，当计算结果收敛时得到的结果见表3。

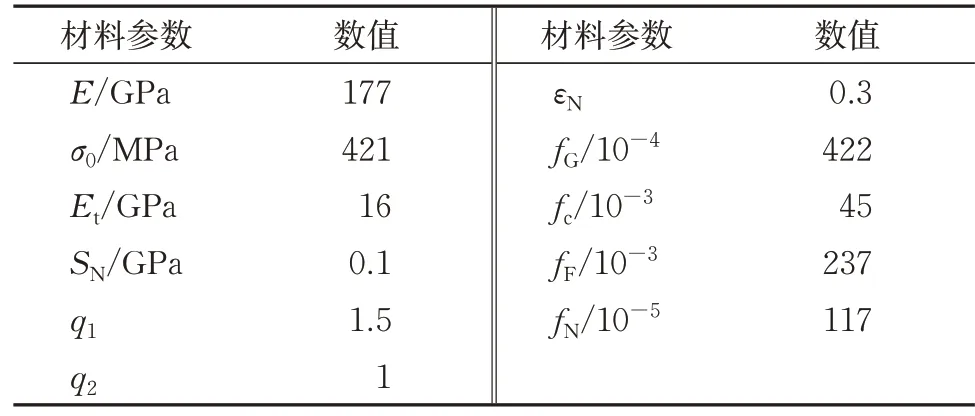
表3 G-T-N模型中的材料参数

4.3 数值模拟与试验结果对比

使用非线性有限元软件LS-DYNA 材料模型库中*MAT_JOHNSON_COOK 和*MAT_GURSON定义材料的断裂模型。在有限元模拟中采用与试验相同的加载及边界条件。得到3 种试样基于G-TN与J-C断裂理论的载荷-位移曲线如图12所示。

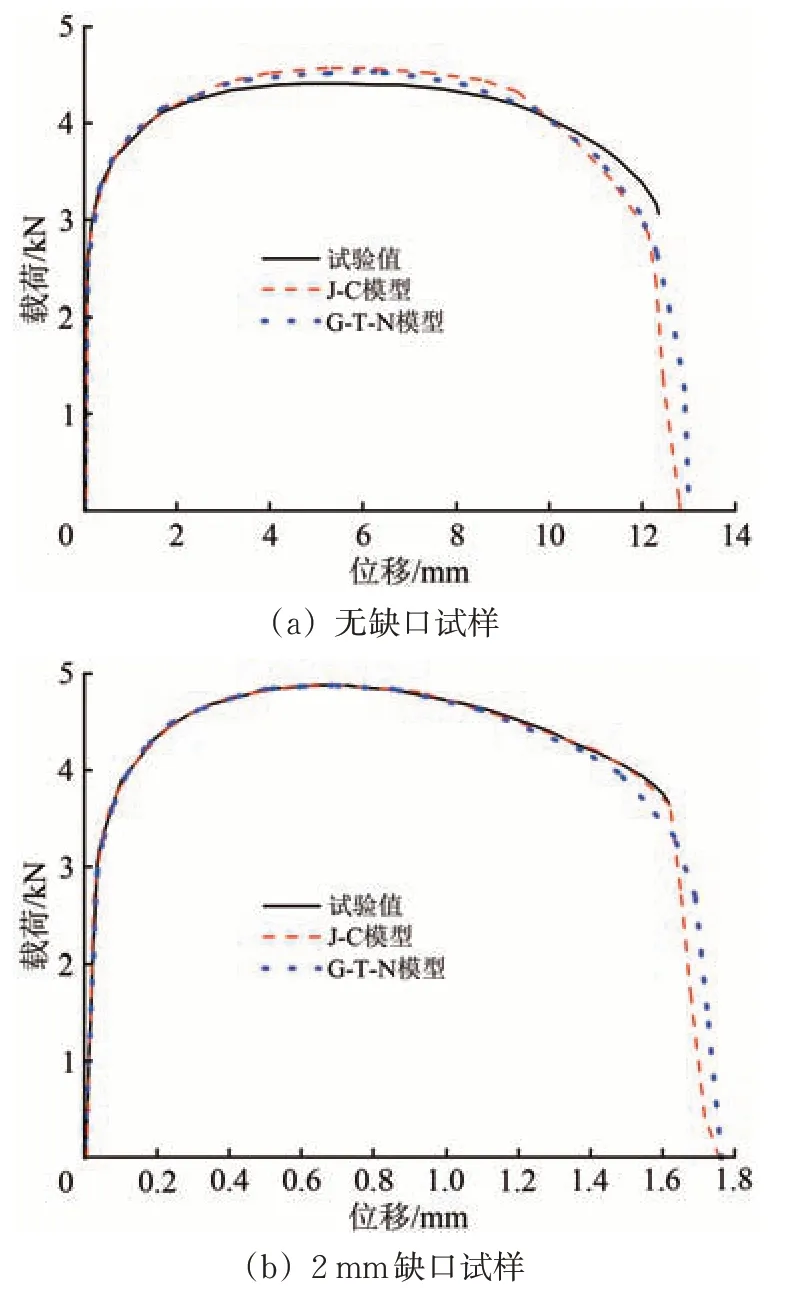
从图12 可以看出：基于G-T-N 与J-C 断裂理论建立的不锈钢断裂数值模拟结果均与试验结果较好地吻合；数值模拟结果表明，当应力状态为高应力三轴度时，基于2 种断裂理论均可以得到比较理想的断裂模拟结果。

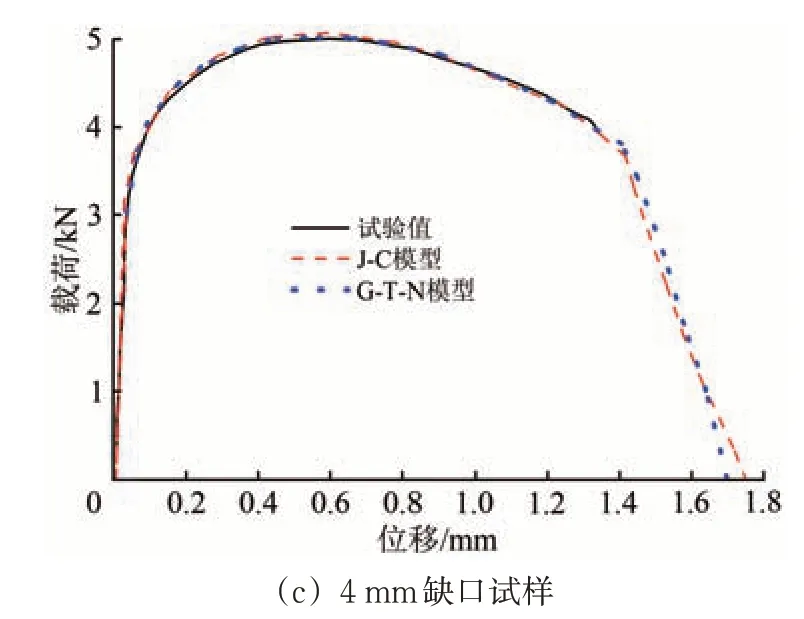
图12 数值模拟与试验结果对比

3 种试样仿真断裂结果与试验结果对比如图13所示。从图13可以看出：3种试样的裂纹从缺口中心处萌生，然后向2 端扩展至断裂；数值模拟结果较好地重现了韧性断裂过程，其扩展路径与试验过程基本一致。

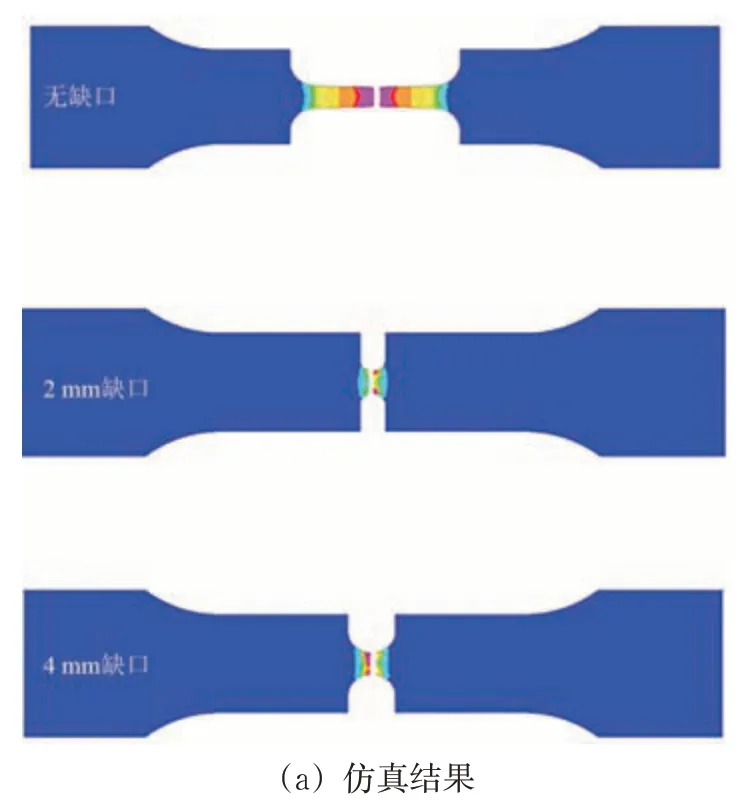
图13 试样仿真断裂结果与试验结果对比

5 结 论

（1）以301L-DLT 不锈钢在不同应力状态下的断裂应变为研究目标，设计了无缺口及2 和4 mm 缺口的3 种试样，并分别进行拉伸断裂试验。试验结果表明：相同宽度的缺口试样，由于缺口处形状的不同，导致了断裂载荷及最大位移均发生显著变化。

（2）通过电镜对拉伸断裂试验的断口观察可以看出，3 种试样断口中心布满韧窝，断裂面为韧窝断裂，是一种典型的高应力三轴度韧性断裂。对拉伸断裂试验过程进行有限元仿真结果表明，3 种试样拉伸断裂试验的应力三轴度分布在0.33～0.81 之间，断裂塑性应变随着应力三轴度的增大从1.41下降到0.78。

（3）基于G-T-N 断裂理论与J-C 断裂理论，建立301L-DLT 冷轧不锈钢断裂模型，并应用有限元方法对3 种不同缺口尺寸的试样进行数值仿真分析。结果表明：数值模拟结果较好地重现了韧性断裂过程，其断裂扩展路径与试验过程基本一致；当应力状态为高应力三轴度时，2 种断裂理论均可以得到比较理想的断裂仿真结果。