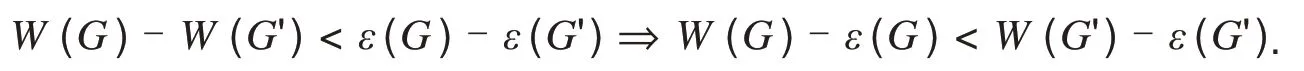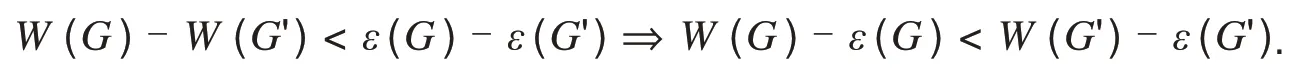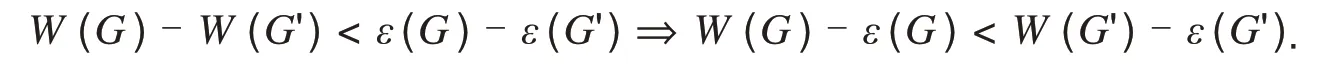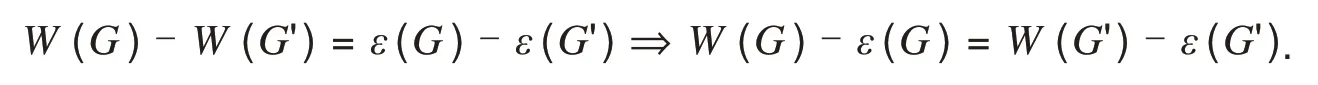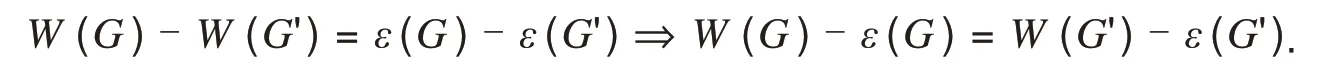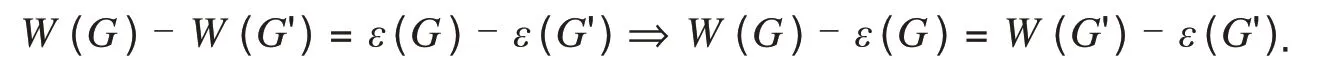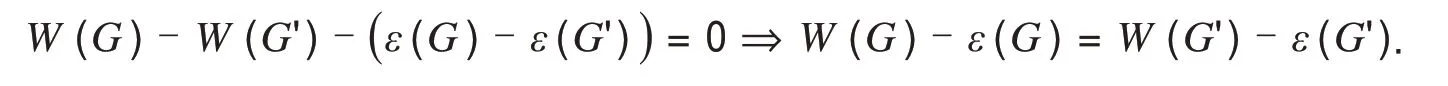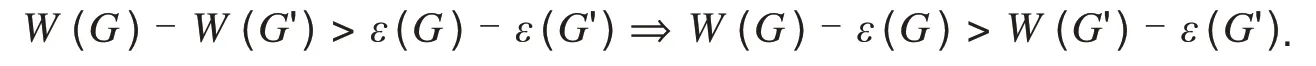一类图变换对其维纳指标与离心率之差的影响
林雅津,王月卿
(1.闽南师范大学数学与统计学院,福建漳州363000;2.闽南师范大学计算机学院,福建 漳州363000)
本文所讨论的均为简单连通图,设G=(V(G),E(G)),其中顶点集为V(G),边集为E(G).用n(G)和m(G)分别表示图G的顶点数和边数.对任意u,v∈V(G),用dG(u,v)表示G中u和v之间的最短距离.用dG(v)表示顶点v到G中其余顶点的距离之和,即分别用deg(v)和ω(G)表示顶点v的度和图G的连通分支个数.若边e∈E(G)满足ω(G-e)>ω(G),则称e为连通图G的一条割边.对于图G的某一割边e=uv∈E(G),分别用n(Gu),n(Gv)表示G中分布在e两侧的顶点数目.
图的维纳指标是1947年由著名的化学家Wiener[1]提出的基于距离不变量的拓扑指标,其定义是图中所有不同顶点对间的距离和,即

关于图维纳指标的研究和进展可参考文献[1-6].
对v∈V(G),顶点v在G中的离心率εG(v)是v与G中其他任意点的最大距离,即

定义G中最大的顶点离心率为直径,用diam(G)表示;最小的顶点离心率为半径,用rad(G)表示.
图G的离心率为G中所有点的离心率之和,用ε(G)表示.因此

关于图的总离心率和平均离心率的研究和进展可参考文献[7-9].若e∈E(G),令G⋅e表示图G通过收缩边e之后而得到的图,显然n(G)=n(G⋅e)+1,如图1所示.

图1 图G和G⋅eFig.1 The graph G and graph G⋅e
1 预备知识
Darabi[10]研究了G和G⋅e的维纳指标和离心率之间差的关系,得到了以下结论.
定理1[10]设G为具有n(G)≥3个顶点的简单连通图,e∈E(G)是G的某一割边,则

同时提出了以下猜想.
猜想1[11]设G为具有n(G)≥3个顶点的简单连通图,则对于任意e∈E(G),有

Das[11]证明了上述猜想.
本文进一步研究图的变换对其W(G)-ε(G)的影响.设G为简单连通图,对e∈E(G),G'为G通过收缩边e=uv成为一个新点eu并在eu上添加一个悬挂边euev而得到的图,如图2所示.

图2 图G和G'Fig.2 The graph G and graph G'
显然图G'对比文献[11]中的图G⋅e来说,保持了顶点数的不变,即n(G)=n(G')=n.本文研究并讨论了当e是图G(n(G)≥3)的割边时,给出了不同情况下W(G')-ε(G')和W(G)-ε(G)之间的大小关系.
在给出结论前,先分析图G和图G'的一些性质.
如图2,令割边e=uv,令G-uv=Gu∪Gv,这里Gu和Gv是分别包含u和v的分支,n(Gu)和n(Gv)分别表示两个分支的顶点数,不妨设n(Gu)≥n(Gv).则

对于G',有

因此W(G)-W(G')=n(Gu)n(Gv)-n+1.
比较图G'和图G,点u在G'对应点eu;点v在G'对应点ev,且保持顶点离心率不变,即εG(v)=εG'(ev).因此变换成G'后离心率最多减少n-1,即
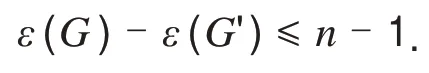
当n(Gv)=2 时,W(G)-W(G')=n-3.将Gu中的点分为S1,S2,…,Si(i=2,…n-3)类,Si表示Gu中与u距离为i的顶点集.点v在G'中对应点ev使得离心率不发生改变,并且当点u存在属于Gu的离心点时,也有点u在G'中对应的点eu的离心率不发生改变.
当n(Gv)≥3,由于n(Gu)≥n(Gv),因此n(G)=n≥6 且W(G)-W(G')≥2n-8,等号成立当且仅当n(Gv)=3.又因为ε(G)-ε(G')≤n-1,所以

等式成立当且仅当n=7.
引理1设G为简单连通图,e∈E(G)为G的某一割边,G和G'如图2所示.若εGu(u)≥4,则对任意x∈S1,有εGu(x)≥3=dG(x,w).
证明(反证法)假设∃x∈S1,使得εGu(x)≤2,即对任意y∈Gu,都有d(x,y)≤2.因为εGu(u)≥4,令u1为u的离心点,即d(u,u1)≥4.取y=u1,则d(x,u1)≤2,因为d(u,x)=1,所以有

又因为εGu(u)=d(u,u1)≥4,与式(2)矛盾,结论成立.
引理2设G为简单连通图,e∈E(G)为G的一割边,G和G'如图2所示.若εGu(u)≥6,则
1)对任意x∈S1,有εGu(x)>3=dG(x,w);
2)对任意y∈S2,有εGu(y)≥4=dG(y,w).
证明由定理1可知,1)显然成立,接下来对2)进行证明.
(反证法)假设∃y∈S2,使得εGu(y)≤3,即对任意y1∈Gu,都有d(y,y1)≤3.因为εGu(u)≥6,令u1为u的离心点,即d(u,u1)≥6.取y1=u1,则d(y,u1)≤3,因为d(u,y)=2,所以有
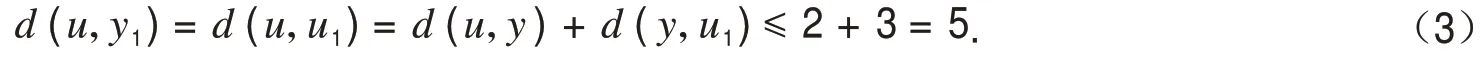
又因为εGu(u)=d(u,u1)≥6,与(3)矛盾,结论成立.
2 主要结论
以下给出不同情况下W(G')-ε(G')与W(G)-ε(G)之间的大小关系,如图2所示.不妨设n(Gu)≥n(Gv),接下来按n(Gv)大小进行分类.当n(Gv)=1,显然有W(G)-ε(G)=W(G')-ε(G').以下讨论n(Gv)≥2的情况,其中n(Gv)=2时如图3所示.

图3 n(Gv)=2的图GFig.3 The graph G of n(Gv)=2
显然对任意x∈Si,都有
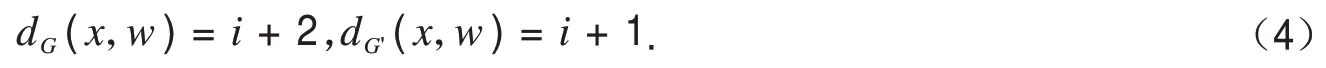
因此若Gu中的点在G中的离心点只有w时,变换成G'后顶点离心率将会减少1.若Gu中的点在G中存在离心点是属于Gu中的话,变换成G'后顶点离心率将会保持不变.
定理2设G简单连通图,e=uv为G的某一割边,G'为收缩G中边e=uv成为一个点eu,并在eu上添加悬挂边euev而得到的图,如图2所示.则以下六种情况都有W(G)-ε(G) 1)当n(Gv)=2,εG(u)=2,且deg(u)=n-2; 2)当n(Gv)=2,εG(u)=2,deg(u)≤n-3且diam(Gu)=2; 3)当n(Gv)=2,εG(u)=2,deg(u)≤n-3,diam(Gu)=3且对∀x∈S1都有εGu(x)=2; 4)当n(Gv)=2,εG(u)=3,deg(u)≤n-4,diam(Gu)=3且对∀x∈S1都有εGu(x)=2; 5)当n(Gv)=2,εG(u)=3,deg(u)≤n-4,diam(Gu)=4 且对∀x∈S1都有εGu(x)=2,对∀y∈S2,都有2≤εGu(y)≤3; 6)当n(Gv)=3,n=6且图G≅P6. 证明1)因为n(Gv)=2,εG(u)=2,且deg(u)=n-2.如图4,此时u的离心点只有w.对∀x∈S1,有εG(x)=dG(x,w)=3.因此εG'(x)=dG'(x,w)=2,又εG(u)=d(u,w)=2,所以由式(4)有εG'(eu)=1.由此可知在这种情况下,G变换成G'后只有一个顶点v的离心率不发生改变,即ε(G)-ε(G')=n-1.因此有 图4 deg(u)=n-2时的图GFig.4 The graph G of deg(u)=n-2 2)当deg(u)≤n-3,又εG(u)=2,所以u在图G中至少有两个离心点.当diam(Gu)=2 时,即∀x∈V(Gu)/{u},有εGu(x)≤2.又因为dG(x,w)≥3,因此εG(x)≥3 且x在G中的离心点均为w,故εG'(x)=εG(x)-1,由式(4)可知G变 换成G' 后只有两个顶点u,v的离心率不发生改变,即ε(G)-ε(G')=n-2.所以有 结论成立. 3)当deg(u)≤n-3,diam(Gu)=3,且对∀x∈S1,都有εGu(x)=2时,有εG(x)=dG(x,w)=3,则由式(4)显然可知对任意x∈S1,都有εG'(x)=εG(x)-1=2.又因为diam(Gu)=3,因此对任意的εGu(y)=3 成立时,都有y∈S2,因此有εG(y)=dG(y,w)=4=dG'(y,w)+1,所以εG'(y)<εG(y).因此对任意y∈S2都有εG'(y)<εG(y),所以G变换成G'后只有两个顶点u,v的离心率不发生改变,即ε(G)-ε(G')=n-2,所以有 结论成立. 4)当εG(u)=3,deg(u)≤n-4,diam(Gu)=3,且对∀x∈S1,都有εGu(x)=2时,有εG(x)=dG(x,w)=3,则显然可知对任意x∈S1,都有εG'(x)=dG'(x,w)=2<εG(x).又因为diam(Gu)=3,即对任意的εGu(y)=3 成立时,都有y∈S2∪S3,因此有εG(y)=dG(y,w)=dG'(y,w)+1,所以对任意的y∈S2∪S3,都有εG'(y)<εG(y).因此G变换成G'只有u,v两个点的离心率不发生改变,即ε(G)-ε(G')-n=2,所以有 结论成立. 5)当εG(u)=3,deg(u)≤n-4,diam(Gu)=4 时,且对∀x∈S1,都有εGu(x)=2,对∀y∈S2,有2≤εGu(y)≤3 时,有εG(x)=dG(x,w)=3,3≤εG(y)=dG(y,w)≤4.则可知对任意的x∈S1,都有εG'(x)=dG'(x,w)=2<εG(x);对任意y∈S2,都有εG'(y)=dG'(y,w)=εG(x)-1.又因为diam(Gu)=3,即对任意的εGu(z)=4 成立时,都有z∈S3,所以对任意z∈S3有εG'(z)<εG(z).因此G变换成G'之后只有u,v两个点的离心率不发生改变,即ε(G)-ε(G')=n-2,所以有 结论成立. 6)当n(Gv)=3,n=6 时,即n(Gu)=n(Gv)=3,这时有W(G)-W(G')=4.又因为图G≅P6,显然ε(G)-ε(G')=5.所以有 结论成立. 定理3设G简单连通图,e=uv为G的某一割边,G'为收缩G中边e=uv成为一个点eu,并在eu上添加悬挂边euev而得到的图,如图2所示.则以下五种情况都有W(G)-ε(G)=W(G')-ε(G')成立: 1)当n(Gv)=2,εG(u)=2,deg(u)≤n-3,diam(Gu)=3且有且只有一个点x∈S1,使得εGu(x)=3; 2)当n(Gv)=2,εG(u)=3,diam(Gu)=3且有且只有一个点x∈S1,使得εGu(x)=3; 3)当n(Gv)=2,εG(u)=3,diam(Gu)=4,∀x∈S2,有εGu(x)≤3,且有且只有一个点y∈S1,使得3≤εGu(y)≤4; 4)当n(Gv)=2,4≤εG(u)≤5,且G≅{P7,P8}; 5)当n(Gv)≥3,且n=7. 证明1)当εG(u)=2,deg(u)≤n-3且diam(Gu)=3时,对任意x∈Gu,都有εGu(x)≤3.又由式(4)可知对任意x∈Gu,都有εG(x)≥3 且等式成立当且仅当x∈S1.因此变换成G'后S2中任意点的离心率均减少1.又因为有且只有一个点x∈S1,使得εGu(x)=3,即S1中的点除了x之外的其余点离心率均为2.因此变换成G'后S1中除了x之外的其余点的离心率均减少1.又点u,v的离心率均不发生改变,所以G变换成G'之后离心率减少了n-3,即ε(G)-ε(G')=n-3.所以有 结论成立. 2)当εG(u)=3,diam(Gu)=3,且有且只有一个点x∈S1,使得εGu(x)=3时,有εG(x)=εGu(x)=3.又由1)的证明显然可知,G变换成G'之后离心率减少了n-3,即ε(G)-ε(G')=n-3.所以有 结论成立. 3)当εG(u)=3,diam(Gu)=4,对任意的x∈S2,都有εGu(x)≤3,且有且只有一个点y∈S1,使得3≤εGu(y)≤4时,由式(4)可知,S2和S3中所有点的离心率在G变换成G'之后均减少1.又因为有且只有一个点y∈S1,使得3≤εGu(y)≤4,所以由1)的证明可知,G变换成G'之后离心率减少了n-3,即ε(G)-ε(G')=n-3.所以有 结论成立. 4)当4≤εG(u)≤5,由引理1 可知,对任意x∈S1都有εGu(x)≥3,因此由式(4)可知G变换成G'后S1中任意点的离心率均不发生改变.又因为G≅{P7,P8},所以有|S1|=1,且由式(4)可知,任意y∈Gu/{S1,u}都有εG(y)=εG'(y)+1.因此G变换成G'之后恰好有三个顶点离心率不发生改变,所以离心率减少了n-3,即ε(G)-ε(G')=n-3.所以有 结论成立. 5)当n=7时,由式(1)有 结论成立. 注1下面分别给出满足上述条件的图例. 满足条件1),如图5. 图5 满足条件1)的图GFig.5 A graph G that satisfies the condition 1) 此时,W(G)-ε(G)=44-23=21,而W(G')-ε(G')=40-19=21,所以有W(G)-ε(G)=W(G')-ε(G'). 满足条件2),如图6. 图6 满足条件2)的图GFig.6 A graph G that satisfies the condition 2) 此时,W(G)-ε(G)=63-31=32,而W(G')-ε(G')=58-26=32,所以有W(G)-ε(G)=W(G')-ε(G'). 满足条件3),如图7. 图7 满足条件3)的图GFig.7 A graph G that satisfies the condition 3) 此时,W(G)-ε(G)=50-28=22,而W(G')-ε(G')=46-24=22,所以有W(G)-ε(G)=W(G')-ε(G'). 满足条件4),如图8. 图8 满足条件4)的图GFig.8 A graph G that satisfies the condition 4) 此时,W(G)-ε(G)=56-33=23,而W(G')-ε(G')=52-29=23,所以有W(G)-ε(G)=W(G')-ε(G'). 满足条件5),如图9. 图9 满足条件5)的图GFig.9 A graph G that satisfies the condition 5) 此时,W(G)-ε(G)=43-23=20,而W(G')-ε(G')=37-17=20,所以有W(G)-ε(G)=W(G')-ε(G'). 定理4设G简单连通图,e=uv为G的某一割边,G'为收缩G中边e=uv成为一个点eu,并在eu上添加悬挂边euev而得到的图,如图2所示.则以下八种情况都有W(G)-ε(G)>W(G')-ε(G')成立: 1)当n(Gv)=2,εG(u)=2,deg(u)≤n-3,diam(Gu)=3 且至少有两个点x,y∈S1,使得εGu(x)=εGu(y)=3; 2)当n(Gv)=2,εG(u)=2,deg(u)≤n-4,diam(Gu)=4; 3)当n(Gv)=2,εG(u)=3,diam(Gu)=3且至少有两个点x,y∈S1,使得εGu(x)=εGu(y)=3; 4)当n(Gv)=2,εG(u)=3,diam(Gu)=4且至少有两个点x∈S2,使得εGu(x)=4; 5)当n(Gv)=2,εG(u)=3,5≤diam(Gu)≤6; 6)当n(Gv)=2,4≤εG(u)≤5,且3≤deg(u)≤n-5(n≥8); 7)当n(Gv)=2,εG(u)≥6; 8)当n(Gv)≥3,且n≥8. 证明1)当n(Gv)=2,εG(u)=2,deg(u)≤n-4,diam(Gu)=3且至少有两个点x,y∈S1,使得εGu(x)=εGu(y)=3 时,由式(4)可知G变换成G'后x,y的离心率不会发生改变.又因为点u,v的离心率也不发生改变,所以G变换成G'后至少有四个点的离心率不发生改变,因此ε(G)-ε(G')≤n-4,所以有 2)当n(Gv)=2,diam(Gu)=4 时,因为S1里的任意点的离心率均小于等于3,所以一定∃x∈S2,使得εGu(x)=4.并且x在Gu中的离心点都在S2中,显然dG(x,w)=dG(x,u)+dG(u,w)=εGu(x)=4,因此有εG(x)=εGu(x)=εG'(x)=4.假设点y∈S2,使得εGu(x)=dG(x,y)=4,则点y的离心率也为4 且离心点为x.所以G变换成G'后至少有四个点的离心率不会发生改变,因此ε(G)-ε(G')≤n-4,所以有 结论成立. 3)当n(Gv)=2,εG(u)=3,diam(Gu)=3 且至少两个点x,y∈S1,使得εGu(x)=εGu(y)=3 时,由1)的证明显然可知G变换成G'后至少有四个点的离心率不发生改变,因此ε(G)-ε(G')≤n-4,所以有 结论成立. 4)当n(Gv)=2,εG(u)=3,diam(Gu)=4 且至少存在一个点x∈S2,使得εGu(x)=4 时,显然点x对应的离心点不可能在S1中,这时我们分两种情况讨论.①若点x对应的离心点y∈S2,则显然有εGu(y)=4,所以G变换成G'后至少有四个点的离心率不会发生改变,因此ε(G)-ε(G')≤n-4,所以有 ②若点x对应的离心点y∈S3,则显然存在z∈S1,使得dGu(y,z)=3.否则若dGu(y,z)≤2,则有εGu(x)=dGu(x,y)≤3 与εGu(x)=4 矛盾.所以G变换成G'后至少有四个点的离心率不会发生改变,因此ε(G)-ε(G')≤n-4,所以有 结论成立. 5)当n(Gv)=2,εG(u)=3,5≤diam(Gu)≤6 时,①若diam(Gu)=5,因为对∀x∈S2,都有εGu(x)≤5,且当εGu(x)=dGu(x,y)=5 时,对应的离心点y一定属于S3中,因此有εGu(y)=5.所以显然图G变换成G'后至少有四个点的离心率不会发生改变,因此ε(G)-ε(G')≤n-4,所以有W(G)-ε(G)>W(G')-ε(G').若εGu(x)≤4,则所有εGu(x)=dGu(x,y)=5 都有x∈S3,且对应的离心点y一定属于S3中,因此有εGu(y)=5.所以显然图G变换成G'后至少有四个点的离心率不会发生改变,因此ε(G)-ε(G')≤n-4,所以有W(G)-ε(G)>W(G')-ε(G'). ②若diam(Gu)=6,因为对任意x∈S1∪S2,有1≤εGu(x)≤5,所以一定存在x∈S3,使得εGu(x)=6.并且x在Gu中的离心点都在S3中,显然dG(x,w)=dG(x,u)+dG(u,w)=εGu(x)=6,因此εG(x)=εGu(x)=εG'(x)=6.假设点y∈S3,使得εGu(x)=dG(x,y)=6,则点y的离心率也为6.所以G变换成G'后至少有四个点的离心率不会发生改变,因此ε(G)-ε(G')≤n-4,所以有 结论成立. 6)当n(Gv)=2,4≤εG(u)≤5,且3≤deg(u)≤n-5(n≥8)时,有|S1|≥2,由引理1 可知,对任意x∈S1都有εGu(x)≥3,因此由式(4)可知G变换成G'后S1中任意点的离心率均不发生改变.又|S1|≥2,所以G变换成G'后至少有四个点的离心率不会发生改变,因此ε(G)-ε(G')≤n-4,所以有 结论成立. 7)当n(Gv)=2,εG(u)≥6时,由定理2可知,对任意x∈S1都有εGu(x)>3,对任意y∈S2都有εGu(y)≥4.因此由式(4)可知G变换成G'后,S1和S2中任意点的离心率均不发生改变.又|S1∪S2|≥2,所以G变换成G'后至少有四个点的离心率不会发生改变,因此ε(G)-ε(G')≤n-4,所以有 结论成立. 8)当n(Gv)≥3,n≥8时,由式(1)有 结论成立.