包带装置轴向连接刚度计算与分析

康士朋， 楼云锋， 王添翼， 丁齐林， 王小卫

(1. 上海宇航系统工程研究所， 上海 201109； 2. 上海航天精密机械研究所， 上海 201106)

在国内外航天领域中，包带装置(clamp band device，CBD)被用于连接卫星与运载火箭。包带装置轴向连接刚度(包带连接刚度)对星箭动力学特性有重要影响[1]。文献[2-3]建立了包带预紧力、轴向载荷与包带连接刚度之间的关系表达式；文献[4-5]进一步建立了轴向激励作用下的包带连接系统动力学模型，分析了对接面角度、包带预紧力、轴向载荷对包带连接系统动力学响应的影响；文献[6]通过对比不同预紧力下有效载荷幅频响应曲线，提出包带预紧力对结构动力学特性具有重要影响，预紧力越小，结构固有频率越低，且非线性现象越明显。

由于包带连接刚度涉及多个部件之间的相互接触，力学行为复杂，因此航天工程中通过包带装置刚度试验获得包带连接刚度。但随着航天任务密集发射以及低成本发射，以试验验证替代设计计算的模式已经不适应航天技术发展趋势。因此，需要开展包带连接刚度计算方法研究。

然而，目前国内外针对包带连接刚度计算方法的研究较少，秦朝烨等[2]基于对接框变形，应用弹性力学理论推导了一定轴向拉力范围内包带连接刚度的解析表达式，并提出通过引入修正系数可以对包带连接刚度解析表达式进行完善。

本文提出一种包带连接刚度解析算法，在考虑对接框变形的基础上，增加了夹块变形的影响，并提出了通过有限元计算结果对数值计算结果进行修正的方法，通过试验验证了该方法的正确性。基于该方法，进一步对包带连接刚度影响因素以及不同预紧力下包带连接刚度特性进行了分析。

1 解析计算方法

1.1 公式推导

包带装置由条带、夹块、爆炸螺栓等零组件构成，如图1所示。通过在条带上施加预紧力，将夹块与上、下对接框进行紧固。在火箭飞行过程中，包带装置承受由卫星传递的力学载荷。

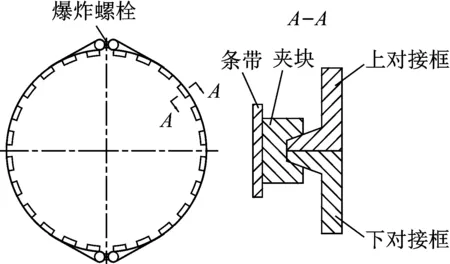
图1 包带装置结构示意图

工程中，包带预紧力常用计算公式[7]为

(1)

包带装置与对接框受力分析包括两部分，包带预紧力载荷下受力分析和对接框当量轴拉载荷下受力分析。本文以单位弧长的包带装置及对接框组合体为研究对象，在施加包带预紧力状态下对其开展受力分析，如图2所示。

图2 条带、夹块、对接框受力分析图

根据包带预紧力与包带装置结构参数，首先计算条带单位弧长力q，计算公式[8]如式(2)所示。根据夹块在水平方向受力平衡方程，得到夹块与对接框接触面压力N计算式(3)

(2)

式中：δ为夹块间隙因子；R为条带中面半径。

(3)

火箭飞行中，包带装置承受当量轴拉载荷。对条带及夹块进行受力分析，如图3所示。包带装置承受轴拉载荷后，对接框与夹块产生径向收缩，包带预紧力变小[9]，减小值ΔT计算公式如式(4)所示。

(a)

(4)

式中：E,A,v分别为弹性模量、横截面面积和泊松比；下标t，d，j分别为条带、对接框、夹块；Rd为对接框中径；Rj为夹块横截面中径。

根据包带预紧力变化值，得到单位弧长力变化值Δq计算式(5)。包带装置承受轴拉载荷后，夹块与对接框之间摩擦力变化方向。根据夹块水平方向受力平衡方程，得到夹块与对接框之间的正压力计算式(6)。

(5)

(6)

式中，ΔN为夹块与对接框之间增加的正压力。

根据式(3)、式(6)，得到ΔN计算公式

(7)

在轴拉载荷作用下，夹块与上对接框、下对接框发生微小的变形，产生转角α，如图5所示。夹块弹性变形产生的转角用αj表示，对接框弹性变形产生的转角用αd表示。包带预紧力计算方法保证图5中A点一直处于接触状态，即上、下对接框在A点相对位移为0。

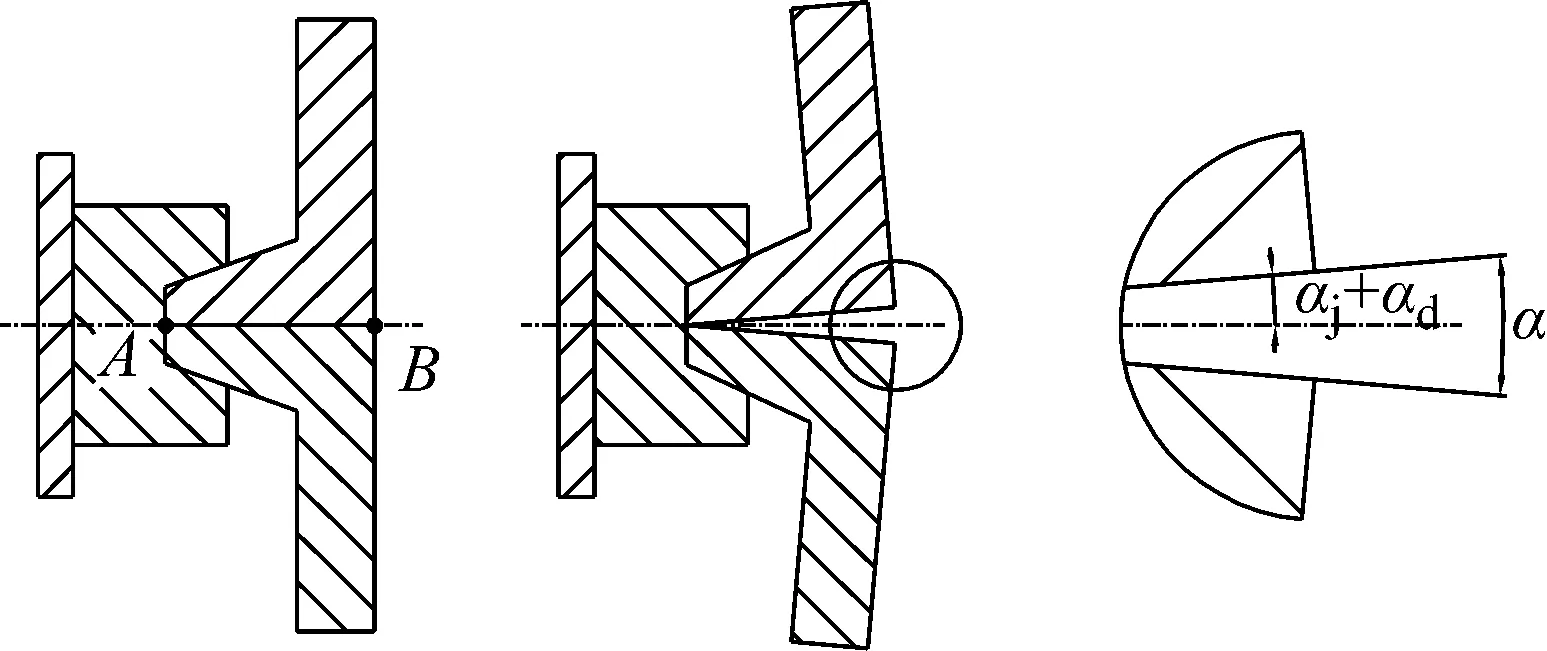
图5 对接面转角示意图

将夹块受到的对称约束及预紧力水平约束，简化为对称面的固定约束,如图6所示。轴拉载荷作用后，夹块与对接框之间接触力增大，增加的接触力使夹块V型面角度变大，对接框随之转动。由于夹块本身的结构刚度足够大于V型面刚度，将夹块V型面简化成悬臂梁，通过悬臂梁转角公式计算接触力作用点的转角，如式(8)所示

图6 夹块转角计算示意图

(8)

式中：Fj=2μNsinθ+ΔN(cosθ+μsinθ)，为夹块压力在轴向分力的增加力；hj为夹块梁截面尺寸；lj为作用力力臂。

将上对接框V型面简化成悬臂梁，如图7所示。将夹块与对接框之间的接触力简化为接触中点处的固定约束。在轴拉载荷作用下，上对接框转角计算公式为

图7 上对接框转角计算示意图

(9)

在轴拉载荷作用下，星箭对接面在B点产生相对位移d，如图8所示，计算公式为

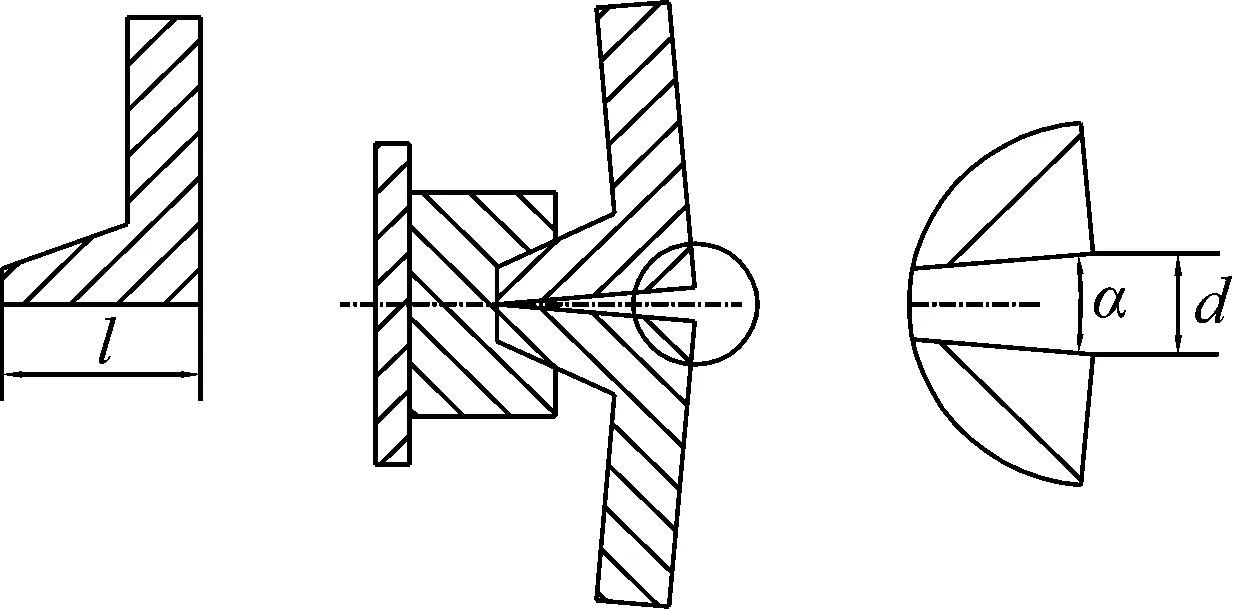
图8 对接面位移示意图

d=2l(αj+αd)

(10)

取上、下对接框在A、B点相对位移的平均值作为对接面脱开距离，得到包带连接刚度计算公式为

(11)

将式(2)～式(10)代入式(11)，得到包带连接刚度计算式(12)

(12)

式(12)表明，包带连接刚度由包带预紧力、轴拉载荷、对接面结构参数、接触面摩擦因数以及包带、对接框材料性能参数确定。

1.2 计算公式修正方法

秦朝烨等对比了计算结果与仿真结果，提出通过引入修正系数可以对包带连接刚度解析表达式进行完善。

1.1节在公式推导过程中，由于将卡块V型面、对接框简化为悬臂梁，使得计算结果带来一定的计算误差。

因此本文提出通过引入边界条件修正系数k0来对计算方法进行修正，修正后的包带连接刚度计算公式为

(13)

1.3 边界条件修正系数k0计算方法

下文将以GJB 4228—2001《卫星与火箭对接尺寸型谱》中937包带装置为例，给出边界条件修正系数k0计算方法以及边界条件修正系数曲线。

为了保证计算结果普遍性，本文以26个计算工况为例，覆盖了937包带装置使用范围，分别采用解析法与有限元法进行包带连接刚度计算，937包带装置的各项参数，如表1所示。

表1 937包带装置参数

根据式(12)以及表1计算参数，计算得到26个计算工况下包带连接刚度计算值，如表2所示。

表2 包带连接刚度计算结果与有限元结果汇总表

有限元计算在包带装置仿真分析中得到了应用：文献[10]通过有限元计算提出采用夹块与对接框发生径向相对滑移作为失效判据来计算包带预紧力过于保守，可采用星箭对接框出现间隙作为连接失效判据；文献[11]通过有限元计算提出通过增加包带预紧力可以提高包带装置承载能力，并指出采用三维全模型进行计算可以获得更准确的计算结果；文献[12]通过有限元计算分析了温度变化对包带装置预紧力的影响。因此，下文采用有限元计算方法对937包带装置26个计算工况下的包带连接刚度进行计算。

根据GJB 4228—2001《卫星与火箭对接尺寸型谱》中937包带装置接口尺寸，建立937包带装置与上、下对接框连接后几何模型，如图9所示。

(a)

对937包带装置模型进行网格划分。夹块、对接框采用实体单元，单元类型为八节点六面体单元SOLID45，单元尺寸为2 mm。由于条带厚度较小，采用壳单元S4R，单元尺寸为4 mm，整个有限元模型单元数为855 617，有限元模型如图10所示。

图10 937包带装置有限元模型图

各零件采用线弹性材料属性，具体如表3所示。有限元模型中，载荷通过接触对进行传递，并在不同接触对中设置实测的摩擦因数[12]。

表3 包带装置材料属性

有限元计算中共分为两个载荷步：第一个载荷步中对爆炸螺栓上施加包带预紧力载荷；第二个载荷步中对上对接框施加轴向拉力载荷。通过计算获得星箭连接面相对距离。

下文以10 000 N包带预紧力计算工况为例，说明连接刚度计算过程，包带装置与对接框变形图(变形比例放大10倍)，如图11所示。

图11 包带装置有限元计算结果示意图

根据包带装置对称性，取包带装置0°,45°,90° 3个典型截面计算结果进行分析，如图12所示。分别提取上对接框、下对接框相对位移值Δl0°，Δl45°，Δl90°，并计算其平均值Δl。

图12 测点位置图

通过有限元计算，得到轴拉载荷以及星箭连接面相对位移数据，对该数据进行拟合，形成相对位移与轴拉载荷的关系曲线，如图13所示。得到该计算工况下包带连接刚度为0.982 3×106N/mm。

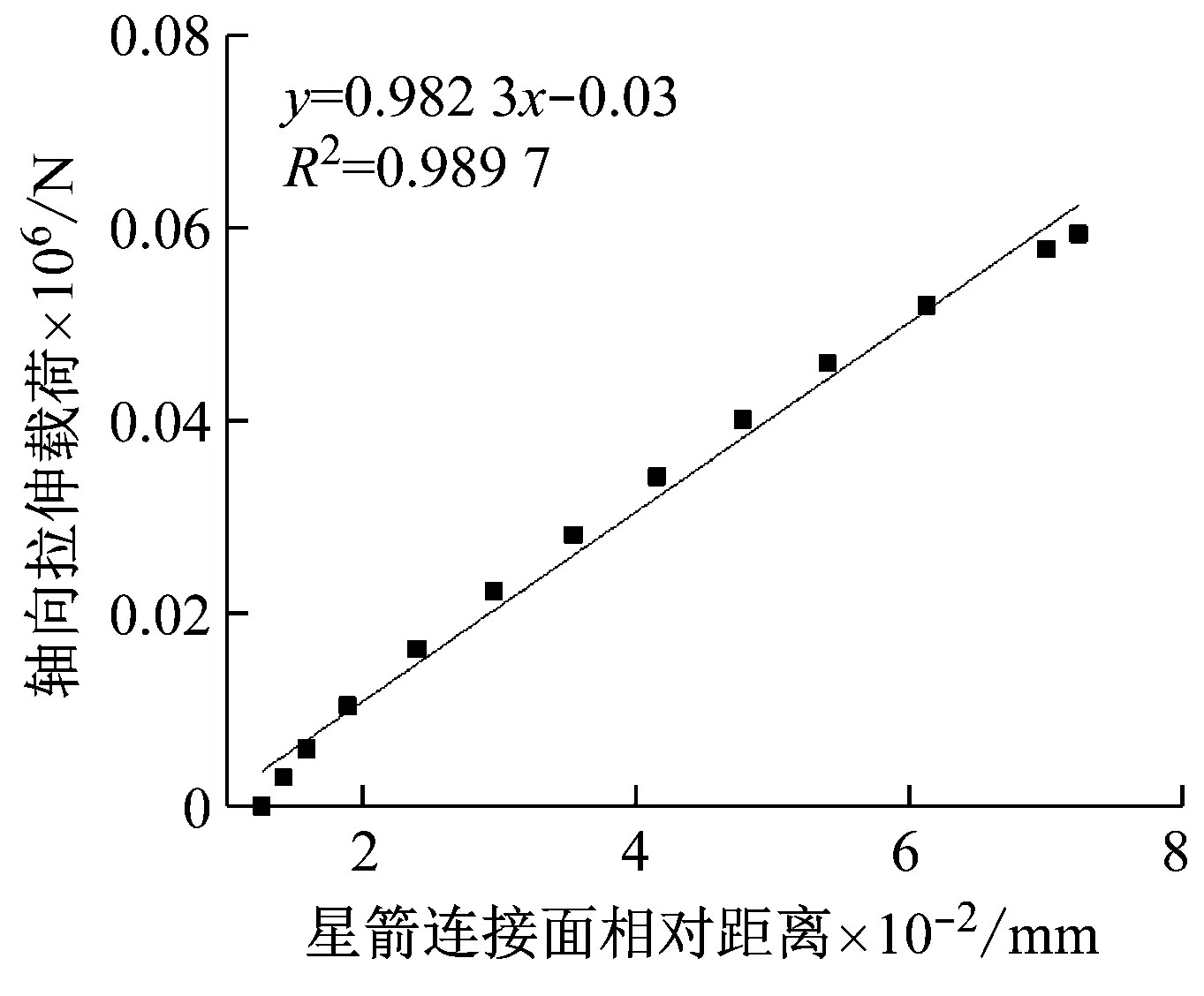
图13 相对位移与轴拉载荷关系曲线

根据以上数据处理方法，得到26个计算工况下937包带连接刚度有限元计算结果，如表2和表4所示。

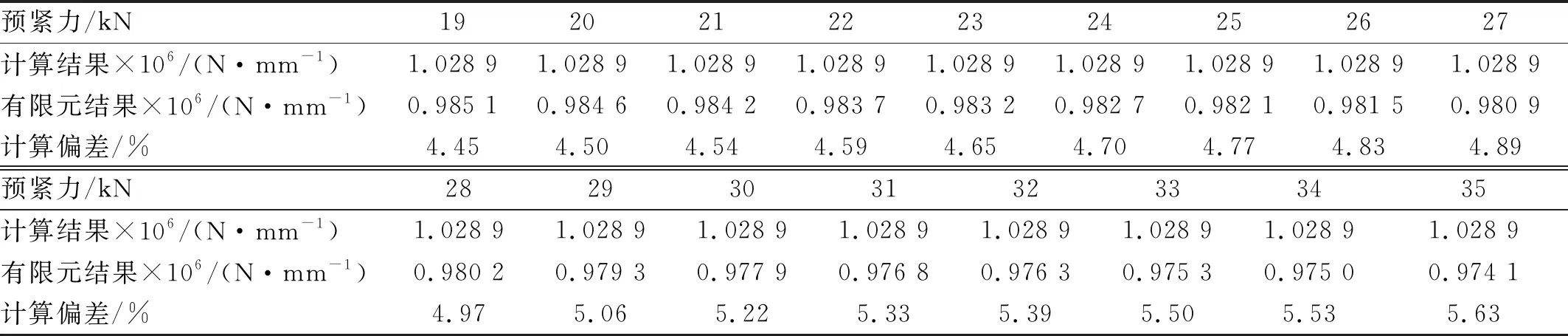
表4 包带连接刚度计算总表

由表2和表4数据可得，计算结果与有限元结果存在4.36% ～5.63%的计算偏差。计算偏差在整体趋势上是随着包带轴拉载荷的增加而增加，计算偏差在整体趋势上与秦朝烨等研究的结论相一致。

根据表2和表4的数据，取有限元结果与计算结果比值作为边界条件修正系数，得到937包带装置边界条件修正系数曲线，如图14所示。

由图14曲线可知，937包带装置包带连接刚度计算公式中边界条件修正系数k0在0.974 1～0.985 9内。通过该曲线可以获得937包带装置在使用范围内不同预紧力下的边界修正系数。

2 算例与试验验证

2.1 算例

以CZ-4C运载火箭发射某试验卫星为例，卫星与运载火箭采用937包带装置进行连接，包带预紧力为15 260 N，包带装置当量轴拉载荷为90 540 N。

根据式(13)、表1计算参数以及由图14得到的边界条件修正系数k0(0.985 8)，得到该使用工况下包带连接刚度计算值为0.971 5×106N/mm。

图14 边界条件修正系数曲线

2.2 试验验证

为了验证计算方法正确性，对2.1节算例开展了连接刚度试验，通过在上对接框、下对接框布置电涡流位移传感器，测量轴拉载荷作用下对接面相对位移，以获得包带连接刚度。

试验在常温常压下进行，试验设备采用MOOG自动协调加载系统、BK-1B型力传感器以及YJ-X4型静态电阻应变仪。力传感器精度为0.5%FS，测量系统精度为±1 με。试验布置如图15所示。

图15 包带连接刚度试验图

在包带装置与上下对接框上布置4对电涡流位移传感器，如图16所示。测量上对接框和下对接框相对位移，其中1′～4′为外侧相对位移测点，1～4为内侧对位移测点。

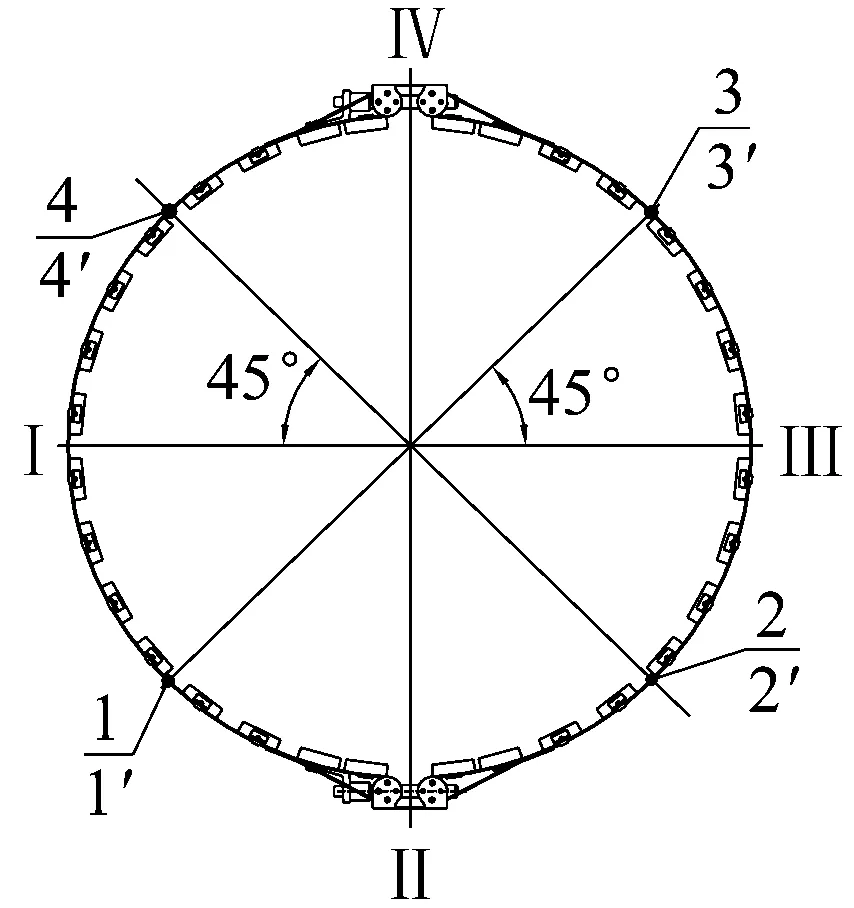
(a)

将下对接框与试验台固连，上对接框与加载工装进行连接。本次试验包带预紧力15 260 N，等效轴拉力为90 540 N。试验过程中以10%为单位进行逐级加载，在每一级加载完成后测量对接面相对位移。本试验开展3次，取3次试验结果的平均值作为最终值。

通过试验，得到不同轴向载荷下对接面的相对位移，如表5所示。

表5 对接面相对位移

对不同轴向载荷以及对接面相对位移平均值进行拟合，形成实测相对位移与轴拉载荷关系曲线，如图17所示。得到实测包带连接刚度为0.942 4×106N/mm。

图17 实测相对位移与轴拉载荷曲线

2.3 试验结果分析

将计算结果与试验结果进行汇总，如表6所示。

表6 937包带装置轴拉刚度计算结果汇总表

由表6可得：解析计算结果与轴拉试验结果偏差为3.1%，表明本文采用的解析计算方法的正确性，可以用于工程载荷范围内包带连接刚度计算。

3 分析与讨论

3.1 轴拉载荷作用下预紧力变化分析

2.1节算例中，包带预紧力为15 260 N，根据式(4)，由于包带装置承受轴拉载荷后，对接框与夹块产生径向收缩，包带预紧力减小值为428.5 N，下降幅度为2.8%。

在不考虑该部分包带预紧力减小值情况下，进行包带连接刚度计算，计算值为0.966 4×106N/mm，计算偏差为0.52%。

计算结果表明，由于包带装置承受轴拉载荷而引起的包带预紧力减小对包带连接刚度影响不大。

3.2 夹块变形对包带连接刚度影响分析

解析计算方法中，除了考虑对接框变形带来的星箭分离面间隙，还增加了夹块变形产生的影响。

对算例结果进行分析，由夹块变形引起的星箭分离面间隙占全部星箭分离面间隙比例为8.3%，对接框变形比例为91.7%，如表7所示。

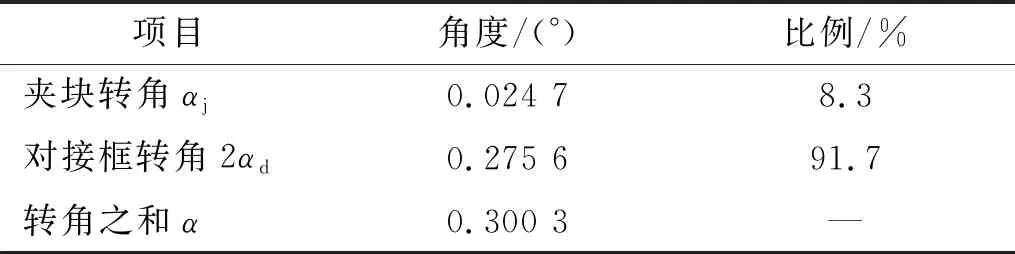
表7 夹块、对接框转角结果

分析表明：对接框变形是影响包带装置轴向连接刚度的最主要因素，但在计算方法中增加由于夹块变形对连接刚度的影响，可以提高计算结果的准确性。

3.3 结构参数对包带连接刚度灵敏度分析

对表1中22个计算参数对包带连接刚度影响影响进行灵敏度分析。选其中8个主要参数，并将8个设计参数的设计值分别增加10%，然后进行包带连接刚度计算，得到计算结果如表8所示。

表8 计算参数灵敏度计算结果汇总表

结果表明，对接框梁截面尺寸、对接框作用力力臂、对接处长度是影响包带连接刚度最主要的设计参数，本节分析结果与3.2节分析结果相一致。

以上3个参数均为星箭机械接口协调中对接框V型面机械接口尺寸参数。因此本计算方法对于星箭机械接口设计具有一定的参考意义。

3.4 增加预紧力对提高包带连接刚度分析

航天工程中，会定性的采用增加包带预紧力的方法来提高卫星连接刚度，但没有定量指标依据做参考，过大增加包带预紧力会降低包带装置强度裕度，并带来较大的包带分离冲击问题。

本节将定量开展包带预紧力对包带连接刚度影响分析，基于2.1节算例，以11个计算工况为例，通过逐渐增加包带预紧力至设计要求值1.5倍以上，分析包带连接刚度变化趋势。

计算结果如表9以及图18、图19所示。

表9 不同预紧力下包带连接刚度

图18 预紧力与包带连接刚度关系曲线

由图18曲线可得，随着包带预紧力增加，包带连接刚度增加，与实际情况相一致；由图19曲线可得，包带连接刚度增加幅度与预紧力增加幅度具有明显非线性特性，具体分析如下：

图19 预紧力变化与包带连接刚度变化对比曲线

(1) 包带预紧力增加在10%内，包带连接刚度同比例增加，表明在该范围内，增加预紧力可以相应提高包带连接刚度，具有明显效果。

(2) 包带预紧力增加在10%～30%内，包带连接刚度增加10%～20%左右，包带连接刚度有一定的提高；

(3) 包带预紧力增加30%后，再增加包带预紧力，包带连接刚度基本不变，表明此时增加预紧力不能提高包带连接刚度。

4 结 论

本文提出了一种包带连接刚度计算方法，在考虑对接框变形基础上，增加了包带装置夹块变形的影响，算例结果表明对接框变形是影响包带连接刚度的最主要因素，但考虑夹块变形影响可以提高计算准确度。

通过引入边界条件修正系数对该方法进行修正，以937包带装置为例，给出了边界条件修正系数曲线。通过开展试验，对该计算方法进行验证，计算得到结果与试验结果进行对比，计算偏差为3.1%，验证了方法的正确性。

进一步对工程中通过提高包带预紧力来提高卫星连接刚度的做法进行定量分析，算例结果表明：包带预紧力增加在10%以内，包带连接刚度同等比例增加；包带预紧力增加在10%～30%内，包带连接刚度只增加10%～20%左右；包带预紧力增加超过30%后，再增加预紧力则不能提高包带连接刚度。

另外，研究发现：由于包带装置承受轴拉载荷而引起的包带预紧力变化对包带连接刚度影响不大。