国内外规范梯度作用下铁路高墩温度效应研究

李 庞

（中铁六局呼和浩特铁路建设有限公司，内蒙古 呼和浩特 010050）

0 引言

截止 2020 年，全国铁路营业里程达到 13.9 万 km，其中，西部地区占比 40.3 %。而我国西部地区地域辽阔，地貌复杂，铁路线路往往会跨越高山、沟谷等地形，高墩大跨桥梁因其跨越能力强，在西部地区得到了广泛的应用。我国西部地区跨越的经度、纬度较大，海拔高度差显著，导致该地区气候复杂多变，温度极值较大，尤其西北地区，年温差多在 50 ℃ 以上，而高墩大跨桥梁的桥墩往往采用空心截面形式，空心墩内部具有气密性，且墩身材料导热性能差，当环境温度变化时，墩壁会产生沿厚度方向的非线性温差，从而产生温度应力［1］。故研究铁路空心高墩的横向温度梯度效应具有十分重要的意义。

在空心高墩的温度效应研究方面，顾皓玮等［2］根据实测数据和传热理论模拟了热力学参数和边界条件，提出了一种柱板式空心高墩温度梯度分布模式；戴公连等［3］采用热－力耦合的三维有限元模型研究了铁路高墩在极值温度下的变形；林国涛等对高墩的温度效应进行了数值分析；刘亚敏［5］研究分析了空心高墩的温度应力；陈贤俊等模拟了日照作用下的空心高墩温度并进行了温度效应分析。现有研究中对于空心高墩沿壁厚方向的温度梯度模式研究较少，且各国规范中大多只给出了梁体的竖向温度梯度。

基于上述现状，本文选取西北地区某铁路空心高墩作为研究对象，建立实体有限元模型，将各国规范中梁体的竖向温度梯度加载至桥墩壁厚方向，对比分析各国规范温度梯度作用下桥墩的温度效应。

1 工程背景及有限元模型

以西北地区某铁路矩形空心高墩作为研究对象，墩高 109 m，材料为 C 35，底部实心段高 2.5 m，顶部实心段高 1.5 m。

采用 MIDAS FEA 建立桥墩及 0 号块实体有限元模型，借助放样、布尔运算等功能建立实体并考虑内、外壁四周的圆形倒角，采用映射功能划分网格，共 50 112 个六面体单元，52 618 个节点。将杆系模型中 0 号块位置处的内力加载至实体模型中 0 号块两侧模拟成桥阶段的边界。有限元模型如图 1 所示。

图1 有限元模型（单位：m）

2 各国规范中温度梯度

2.1 中国铁路规范

根据 TB10092－2017《铁路桥涵混凝土结构设计规范》［7］，沿梁高方向的温度梯度按图 2 进行计算。

图2 中国铁路规范温度梯度

其梯度按指数函数变化，α为沿竖向温差曲线指数，正温度梯度时取 5，负温度梯度时按 10 考虑。

2.2 英国规范

英国 BS5400 规范中关于箱梁的竖向温度梯度考虑了桥面铺装层的影响，按折线变化，且正、负温度梯度的变化规律不同［8］，如图 3 所示。

图3 英国 BS 5400 规范温度梯度

在空心墩温度梯度效应计算时，由于空心墩内部封闭，不存在日照升温现象，墩身温度沿壁厚自外向内逐渐减小，将箱梁温度梯度加载至桥墩时，可忽略梁体底部的温度变化。正温度梯度下取 T1 为 15.4 ℃，T2 取4.5 ℃；负温度梯度下取 T1 为 -13.7 ℃，T2 取 -1 ℃。

2.3 美国规范

美国 AASHTO 规范中，将国土分为四部分，每一部分对应的温差不同，但箱梁的正、负温度梯度变化趋势相同，且其分别对有、无沥青覆盖层做了温差的修正［9］，如图 4 所示。

图4 美国 AASHTO 规范温度梯度（单位：mm）

将箱梁温度梯度加载至桥墩时，可忽略梁体底部的温度变化。正温度梯度下取 T1 为 30 ℃，T2 取 7.8 ℃；负温度梯度下取 T1 为 -15 ℃，T 2 取 -3.9 ℃。

2.4 德国规范

德国 DIN 101 将结构构件的温度梯度分解为温度常量、线性温差和非线性温度分布 3 个部分［10］，如图 5 所示。在桥梁结构中计算温差效应时，可忽略非线性温度分布。

图5 德国 DIN 101 规范温度梯度

在空心墩温度梯度效应计算时，其温度梯度模式按规范中的混凝土板梁取值，正温度梯度下取最大温差为 22.5 ℃，负温度梯度下取最大温差为 -12 ℃。

2.5 新西兰规范

新西兰桥梁设计规范中，在距梁顶的 1.2 m 范围内，其温差按五次抛物线变化［11］，如图 6 所示。

图6 新西兰桥梁设计规范温度梯度（单位：mm）

将箱梁温度梯度加载至桥墩时，可忽略梁体底部的温度变化。正温度梯度下最大温差为 32 ℃，负温度梯度下最大温差为 -16 ℃。

3 温度梯度效应计算结果

在正温度梯度时，仅考虑单向日照作用，即横桥向日照和顺桥向日照，日照面与非日照面墩外壁温度相差 10 ℃。顺桥向日照时墩截面面积较大，在结果分析时仅给出顺桥向日照作用下的正温度梯度响应。

3.1 正温度梯度

正温度梯度下，各规范温度梯度作用下桥墩内、外壁面位移规律基本一致，在此仅给出受阳光直射的外壁面沿墩高的位移曲线，如图 7 所示。

图7 正温度梯度作用下桥墩位移

由图 7 可知：①英国 BS5400 规范、美国AASHTO 规范、德国 DIN101 温度梯度作用下，空心墩外壁位移基本一致，墩顶位移达到 21.4 mm；②新西兰桥梁设计规范和中国铁路桥梁规范温度梯度作用下，墩身位移变化较平缓，墩顶位移分别为 8.7 mm 和 5 mm；③所有规范温度梯度作用下，空心高墩底部均出现了不同程度的反向位移，英国 BS5400 规范温度梯度作用下的反向位移达到了 1.1 mm，这是由于在有限元模拟时墩底截面所有节点均固结，在升温作用下混凝土发生热膨胀产生的位移无法向相邻界面传递，导致墩底局部位置隆起。

正温度梯度作用下向阳面桥墩外壁 von Mises 应力沿墩高分布曲线如图 8 所示。

由图 8 可知：①各国规范温度梯度作用下，接近墩底墩高 1.5 m 处 von Mises 应力较大，最大可达 17.56 MPa，这是由于墩底完全固结导致的应力集中现象。②墩高自10～105 m，各规范作用下 von Mises 应力基本保持不变，其数值为“新西兰规范＞中国规范＞美国规范≈德国规范＞英国规范”。为进一步探究各国规范温度梯度作用下空心高墩的应力状态，取 4 个特征截面（墩高 3、29、68、107.5 m，墩高由低至高依次编号为1-1～4-4）。各特征截面向阳侧 von Mises 应力由外表面至内壁变化如图 9 所示。

图8 正温度梯度作用下 von Mises 应力

由图 9 可知：①各特征截面 von Mises 应力自外壁面至内壁面逐渐减小，至距外壁面 0.5 m 后趋于稳定；②墩高越高，各国规范温度梯度作用下的 von Mises 应力趋于稳定后的值越接近，4-4 截面内壁面 von Mises 应力最大相差 0.71 MPa；③由图 9（a）可知，墩底附近截面的内侧 von Mises应力，其数值为“英国规范＞德国规范＞美国规范＞新西兰规范＞中国规范”。

3.2 负温度梯度

正、负温度梯度作用下，von Mises应力沿墩高分布规律基本一致，在此仅给出负温度梯度作用下各特征截面沿壁厚方向的应力曲线，如图 10 所示。

由图 10 可知：①各截面 von Mises 应力自外壁面至内壁面逐渐减小，1-1～3-3 截面在距外壁面 0.5 m 后趋于稳定，4-4 截面在距外壁面 0.5 m 后仍有一个较为缓和的减小趋势；②墩高越高，各国规范温度梯度作用下的 von Mises 应力在靠近内壁位置的值越接近；③由图 9（a）可知，墩底附近截面的内侧 von Mises 应力，其数值为“德国规范＞英国规范＞美国规范＞新西兰规范＞中国规范”；④由图 9（b）、（c）、（d）可以看出，各截面 von Mises 应力自外壁面至内壁面减小后，在距外壁面 0.3～0.5 m 范围内有一个明显的上升段，上升段最大差值 0.3 MPa。

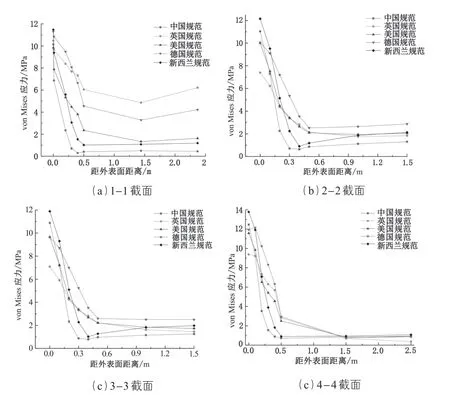
图9 正温度梯度作用下特征截面 von Mises 应力

图10 负温度梯度作用下特征截面 von Mises 应力

4 结论

1）各国规范正温度梯度作用下，墩身位移沿墩高逐渐增大，英国、美国、德国规范温度梯度作用下的位移曲线基本一致，且墩顶位移较大，新西兰规范次之，中国规范温度梯度作用下的位移曲线增长最为平缓，墩顶位移也最小。

2）各国规范正、负温度梯度作用下，von Mises 应力沿墩高变化趋势相同，其数值为“新西兰规范＞中国规范＞美国规范≈德国规范＞英国规范”，von Mises 应力沿壁厚均由外向内逐渐减小，达到一定距离后趋于稳定，且随着截面高度的增加，达到稳定后各国规范温度梯度作用下的应力值趋于一致。

3）墩底局部区域内，各国规范温度梯度作用下的von Mises 应力值相差较大，正温度梯度作用下英国规范最大，负温度梯度作用下德国规范最大，正、负温度梯度作用下中国规范的应力均最小。Q