无穷级数在斐波那契数列相关性质证明中的应用
2021-10-18 11:35:04孙卫卫
黑河学院学报 2021年9期
孙卫卫 王 丹
(青岛城市学院,山东 青岛 266106)
1 斐波那契数列及其相关性质
斐波那契数列[1]是数论中常见的数列之一,该数列又被称为黄金分割[2]数列。斐波那契数列由数学家莱昂纳多·斐波那契(Leonardoda Fibonacci)以兔子繁殖为例引入,故又称为“兔子数列”。该数列具体为:0、1、1、2、3、5、8、13、21、34、……,可以由以下递推公式所得到
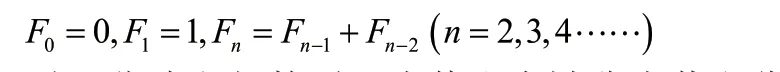
对于斐波那契数列,为什么会被称为黄金分割数列呢?其实不难发现斐波那契数列具有以下性质:
性质一 当n越大,Fn越接近,其中为黄金分割率[2],
例如,当n=8时,F8=21,而,
当n=14时,F14=377,而;
例如,当n=8时,F8=21,F9=34,而
当n=14时,F14=377,F15=610,而。
就因为以上性质,所以,斐波那契数列被称为黄金分割数列,下面运用无穷级数的相关知识给出这两个性质的证明。
2 运用无穷级数对斐波那契数列的性质进行证明
2.1 性质一的证明
证明:先构造如下无穷级数[3]
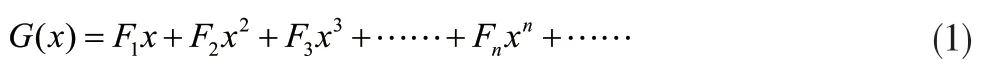
在等式(1)两边乘以x与x2得到如下两个等式
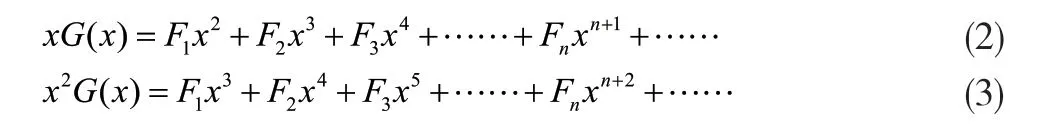
用(1)-(2)-(3)得到
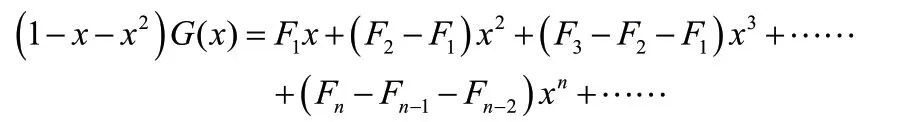
运用斐波那契数列的定义可知F1=1,F2-F1=0,Fn-Fn-1-Fn-2=0(n=3,4,5……),代入上式得到
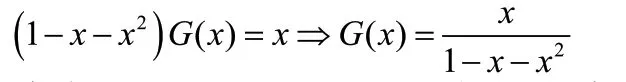
事实上,G(x)也可以展开成x的无穷级数,运用高等数学的相关知识将G(x)分解[4]为如下等式
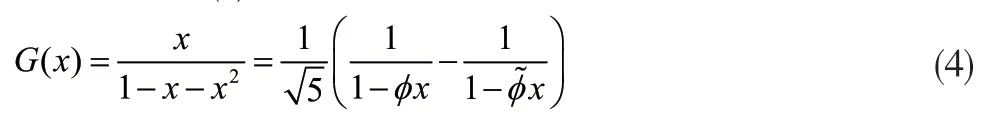
由无穷级数中幂级数展开[3]的相关知识可得
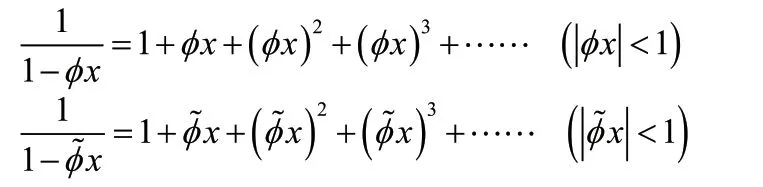
将上式代入(4)式可得
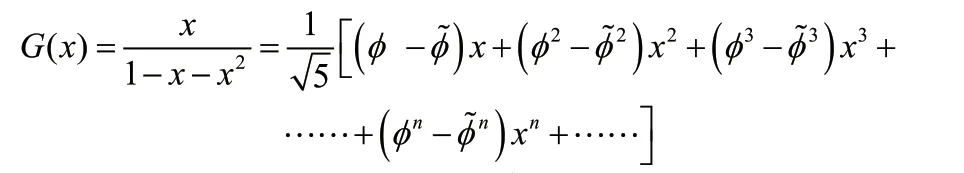
2.2 性质二的证明
证明:根据性质一:当n充分大时,Fn就越接近于因此可得:当n充分大时,就越接近于性质二得证。
猜你喜欢
数学年刊A辑(中文版)(2018年1期)2019-01-08 01:58:22
新高考·高一数学(2017年4期)2017-07-14 01:08:12
数学小灵通·3-4年级(2017年4期)2017-05-04 04:08:30
新高考·高一数学(2016年4期)2016-12-02 03:52:40
山西大同大学学报(自然科学版)(2016年4期)2016-11-27 02:20:55
初中生世界(2016年18期)2016-06-06 08:01:44
学生天地(2016年16期)2016-05-17 05:46:08
初中生世界·八年级(2016年5期)2016-05-14 09:51:15
山西大同大学学报(自然科学版)(2016年6期)2016-01-30 08:29:13
新高考·高二数学(2015年4期)2015-08-20 18:40:15

