基于进化计算的符号网络社区检测
谭玉玲
(罗定职业技术学院 信息工程系,广东 罗定 527200)
在现实生活,许多事物可以被抽象地表示成一些带属性节点,并且事物相互的各种关系被抽象为节点相互的连边,这样可以把想要研究的某些事物和他们之间的联系看作以网络的形式存在。相关人员称由这样的节点和边构成的图为社会网络[1]。例如:包含学者、论文、会议等多种节点和关系的学术网络也被认为是一种广义的社会网络。
社区结构为社交网络均具备的属性,即一些个体具备类似甚至一样的特点,它们相互关系颇为密切。简而言之,社区内的边密度很高,众多社区构成复杂网络[2]。任意提供网络并识别其中隐藏的社区结构的流程即为社区检测,社区结构能够更准确地知晓这个网络的特征与构造。相同社区内部的行动者之间的相似性很强,如它们有共同的兴趣、有共同的目标、参与共同的活动或者组织等。因此,社区检测是社会网络研究的重要内容之一,具有重要的理论和实际价值。
根据不同的社区定义,研究人员发掘出许多的社区检测策略[3]。经典社区检测策略包括图分割,分区聚类,层次聚类和模块化等[4]。图分割法须要事先定义社区总数,且多次二分选代的方式难以得到最优的结果[5]。分区聚类法则是把网络中所有的点对应到高维坐标域中,将距离近的点划分到一起,最后形成预定数目的社区。最常用的分区聚类法K-means法,以及模糊K中心聚类方法[5]。层次聚类法的思路则是源自社会学家。它认为社会网络中节点的聚集是分层次的,大簇中包含着小簇,包括凝聚和分裂层次聚类法。它不需要像图分割法预知社区数目和规模。分裂层次聚类是自上而下的,即从整个网络出发不断移除边得到分割的社区。最具影响力的分裂层次聚类算法是由Newman与Girvan开发的GN算法[6]。其根本思路是认为边的中心性越高,越有可能是连接不同社区的边。所以该算法首先估计所有边的中心性,迭代地将中心性高的边移除。除了依据中心性移除边外,文献[7]提出还可以按照闭环(闭合且不相交的路径)数目移除边;文献[8]提出不只是移除边,移除节点也可以。凝聚层次聚类与其相反,是自下而上从小群组出发经过拼凑得到大社区。文献[9]改善了凝聚层次聚类容易出现不平衡合并的问题。
在符号网络中,各个社区外正向连线稀疏同时负向连线稠密,相同社区的情况反之。基于模块度的研究方面,文献[9]扩充了Potts,使其适用于符号网络社区划分。文献[10]提出在传统模块度计算方式的基础上改进出了引入负向关系的模块度计算方式;文献[11]将失败值和模块度两者的理论有机融合,开发了多目标的符号网络社区检测策略,其最大限度地减少了失败值,并且让模块度趋向最大;文献[12]以模块度理论为基础加以改进,给出模块密度的定义。
在依据聚类的研究方面,文献[13]首先其改造成聚类问题,并说明了两个主要的聚类方向:首先,减少社区内部负向与社区之间的正向聚集,然后是社区内正向与社区之间的负向聚类。文献[14]提出一种改进方法,社区内的负向联系最小,社区之间的正向联系最大,并提出了所对应的目标函数;文献[15]使用模拟退火算法来优化目标函数值,但没有考虑边的密度。该类方法使用时,必须提前知道划分结果的数量,才能得到理想的结果,具有很大缺点。为此,文献[16]提出了FEC算法,具备优秀的时间性和识别精度,但具有不确定性;继而文献[17]将其优化,使其在稳定性等性能取得了重大进展。此外,还有基于谱聚类的策略,适用于符号网络的均衡归一方法[18]。
如上所述,当前对符号网络社区检测算法的方向是优化经典社区检测目标函数;另一种是将符号网络划分为两个完全正负的子网。前者须要提前设定社区的规模,算法的稳定性低,时间和空间复杂度高。后者比较灵活,能够把当前的传统社区检测策略运用于符号网络社区检测。基于此,本文结合图论的理论知识,提出一种改进的进化算法用于符号网络社区检测,设计了基于标签传播的种群初始化、改进的双点交叉算子、带局部搜索的突变算子等,通过基准网络和随机网络进行实验效果验证,结果表明,本文提出的算法具有较高的社区检测率。
1 符号网络中的社区检测
符号网络代表网络用户之间的正负向关系,其中正向关系可以表现成友谊与热爱,负向关系可以表现成敌意与厌恶。如在人际交往中有友好与对立关系,生物界中一些生物激素之间有促进与抑制的关系。符号网络是一类既有正向关系又有负向关系的独特的社会网络,也具有社区结构特点。拥有共同特点的节点可以于符号网络中被发现,由于基本所有网络节点都根据各自的概率连线,连线最稠密的节点是良好集群,它们构成一个社区。在符号网络中去关系划分与一些拥有相同特征的节点识别,有助的信息扩散和链路预测。
1.1 符号网络定义
符号网络模型可以抽象为图形SG=(V,EP,EN),其由一组顶点V,一组正边集EP和一组负边集EN组成。节点的数量由N=V表示,正边的数量由M+=EP表示,负边的数量由M-=EN表示。图1显示了一个基本的符号网络,其中,实线是正向关系,虚线是负向关系,其来源于美国法院九名大法官投票的抽象:若某法官投票赞成其他法官的方案,那么两人存在正向关系,用实线连接;反之用虚线连接。
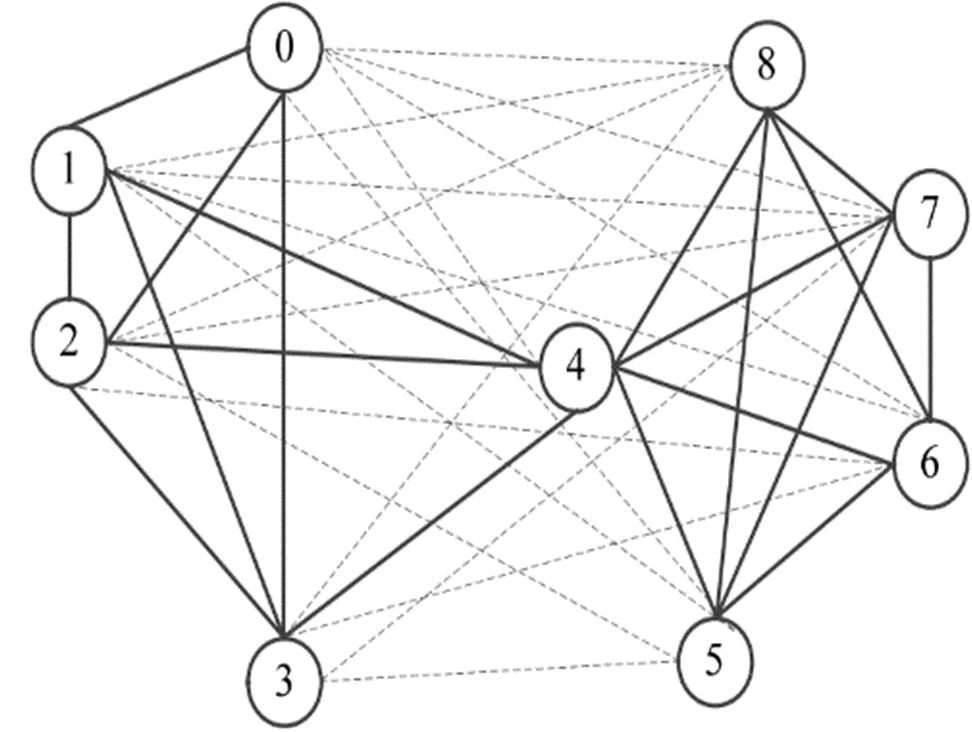
图1 符号网络示意图
1.2 符号网络的社区结构
根据符号的正负进行子矩阵的划分,该问题可以被视为多目标优化问题[18]。其中一个目标是最大限度在不同社区之间放置全部负向连接,另外一个目标就是最大限度地将全部正向连接放入同一社区。在图2社区划分中,社区内有23个正向联系,社区之间有4个负向联系。现实中,不同的划分结果具备不同的实际意义。
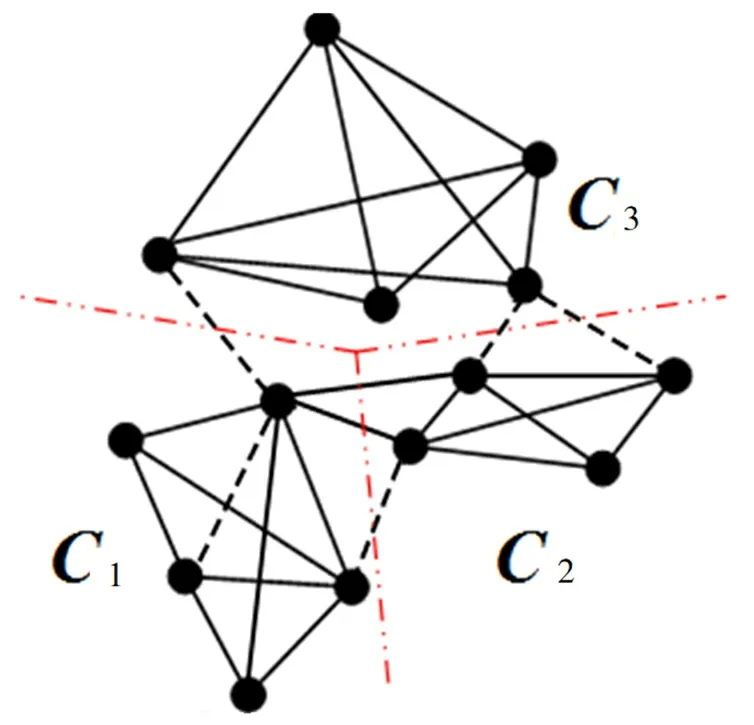
图2 符号网络的社区结构
1.3 社区检测的目标函数
从数学观点来看,符号网络的每个节点连接情况可以由加权邻接矩阵Aij表示,矩阵中元素aij等于1代表节点Vi和节点Vj是正向连接,aij=-1代表节点Vi和节点Vj是负向连接,aij=0代表节点Vi和节点Vj无任何连接。已有的研究采用有符号属性的邻接矩阵划分为两个不相关的矩阵的算法,其中以元素的符号作为分割边界[19]。因此,改进的模块度函数适用于节点之间具有负向边的网络中的社区检测问题。将全正矩阵和全负矩阵划开,如式(1)和(2)所示。
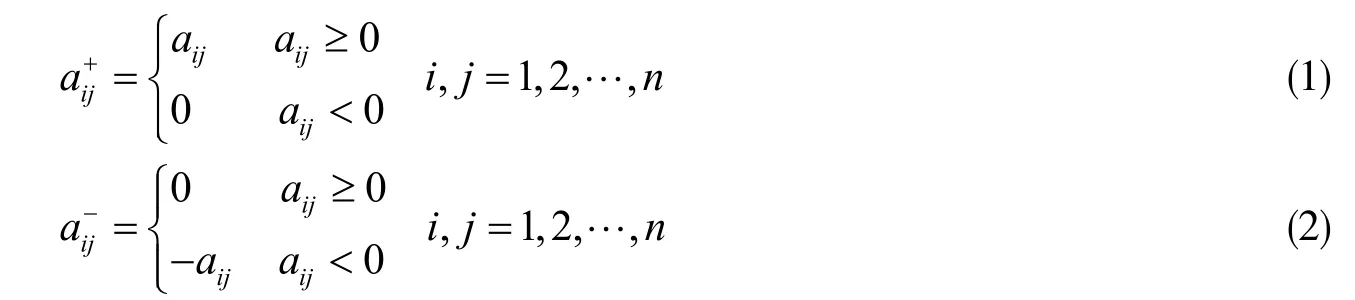
依据权值正负号进行分离,获得全正邻接矩阵A+和全负邻接矩阵A-。
正关系与负关系模块强度用式(3), (4)定义:
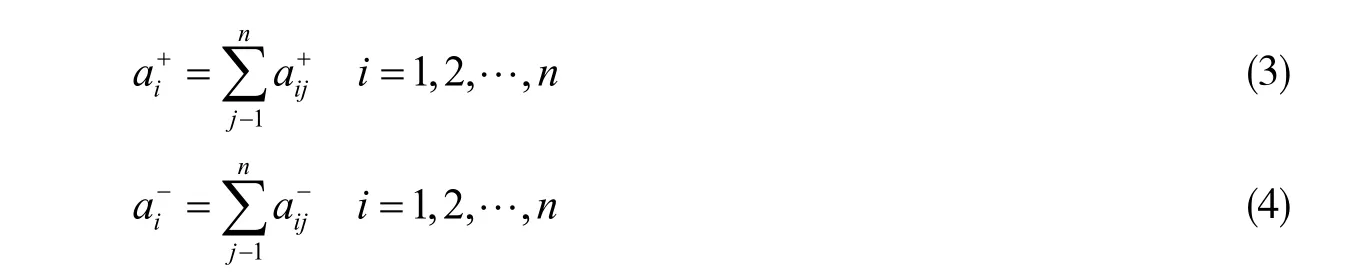
到此,得到正向和负向模块度的两个定义式:
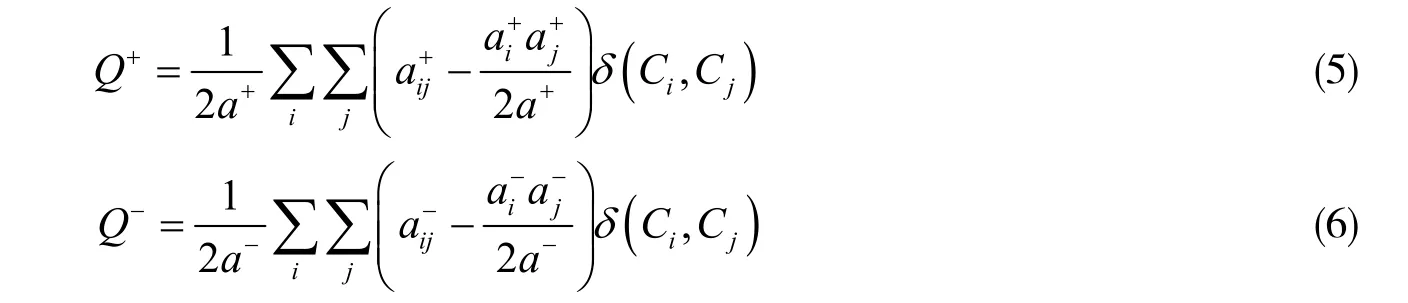

即若节点Vi与节点Vj来自相同社区时,罚函数的值得1;否则得0;罚函数可以把有约束的问题化为无约束问题求解。
因为应当优化Q+与Q-并一起达到最值,得到式(8):
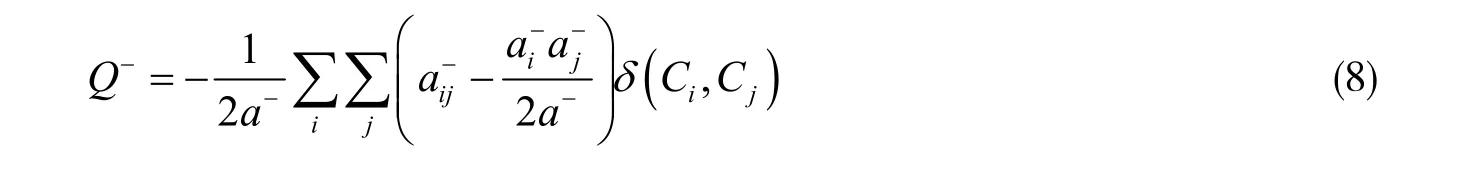
1.4 符号网络的评价指标
通常使用归一化互信息NMI(Normalized Mutual Information)和模块度Q(Modularity Qsign)用于评估符号网络社区检测的性能[20]。本文用到的评价指标为NMI和Q。
NMI一般用来检查社区检测中对检测结果准确性的指标,其数值表达了得到的社区与现实中社区的相似程度,NMI值是0~1,若NMI取值为0,说明检测结果一点也不等同与现实情况,若NMI取1,反之,其定义公式如式(9)。
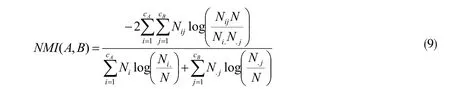
式中,cA是真实存在于网络中的社区数目;cB是检测获得的总社区数;N是矩阵中一行元素的数目;Nij是真实i号的节点与检测到j号社区的节点一致的数目;Ni.与N.j分别对应矩阵里i和j元素之和。
此外,模块度数值可用于评估社区检测结果的优劣程度。值越大,说明网络社区情况越接近真实社区,反之同理。
2 基于进化计算的符号网络社区检测实现
2.1 算法步骤
本文提出的算法具体步骤如下:
(1)总进化次数gen;置初始进化次数t= 1,以IGLP标签传播算法进行种群的初始化操作,获得最初代的种群P0,进而获得t代双亲Pt,Pt=P0;Greatest初始为空,随后选出Pt中最优个体加入其中。
(2)对Pt进行随机联赛选择。
(3)对选择后得到的种群进行变异操作;依据动态交叉概率采用均匀交叉算子或者两点交叉算子;
(4)依据动态交叉概率来判断是进行对应的交叉操作还是LMA突变操作。随后得到子代Qt。
(5)对子代Qt进行适应度由高到低排序,排序第一的个体即为本次进化后最优个体。
(6)若t等于gen(设定的迭代次数),输出最终结果,进化结束;否则,输出当前NMI值,执行(7)。
(7)Pt+1=Qt,t=t+1,返回(2)。
2.2 关键技术说明
2.2.1 初始化算子:IGLP标签传播算法进行初始化
传统算法通常使用随机分配的初始化方法来填充初始化,然而此策略对该问题效果不好,随机数不能反映在符号网络中某些连接密集的点集群[21]。所以,我们在随机赋值后使用了一种标签传播的种群初始化IGLP(Individual Generation via Label Propagation)[22]。在IGLP中,每一个节点所属社区号设置为其相邻接点多数所属的社区号。在这个过程中,具有密集联系的节点均设置为相同的社区号,从而形成了社区。给出某个符号网络,其中有n个节点,m条边,C1,C2, …,Cp,表示下标号节点的所属社区,Cx(d)是第d代第x个社区。
IGLP初始化算子描述如下:
(1)将所有节点的社区标签初始化为随机不同的社区,并将每个节点Vx所属社区Cx(0)设置为1到n之间不同的数字,数字代表对应的社区。
(2)d= 1。
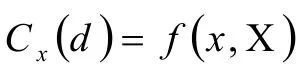
(4)若所有节点已经变化为拥有相邻节点数量最多的标签号,那么初始化算子终止;不然,d=d+1,执行操作(3)。
2.2.2 交叉算子:改进型两点交叉算子
两点交叉思路为在父母染色体上选出2个位置作为穿插点,父母两个穿插点之间的基因片段进行交换产生两个孩子。
本文在原有两点交叉的基础上进行改进,让一对父母杂交N次产生2N个孩子,在2N个孩子中选择适应度最强的两个孩子加入子代种群,这样既可以扩大种群多样性,又能加快进化速度。
详细操作过程是:
(1)选择父母种群中2个不相似的个体作为父母。
(2)在父母的染色体上中随机地选出2个穿插点。
(3)将父母两2穿插点之间的基因片段互换,产生2个孩子。
(4)返回(2)重复到(4)过程N次,产生2N个孩子。
(5)筛选2N个孩子里适应度排名中前2名的孩子添加进子代种群。
(6)判断子代种群是否已满;是,则结束交叉算子;否则,继续产生随机数判断接下来是通过交叉还是突变产生孩子。
图3显示进行一次两点交叉操作的过程图。
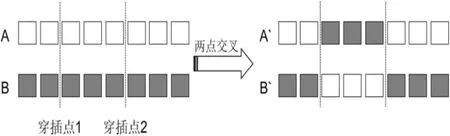
图3 两点交叉运算过程图
2.2.3 突变算子:具有局部搜索的LMA突变算子
具体来说,本文使用的该算子属于突变算子中非均匀突变算子。它允许个体在解空间内移动,但是,对于某个关键部分的搜索却不方便。为了改善这种状况,需要进行随机地干扰初始基因。将干扰得到的基因拿来替换突变后的基因,再用相等的概率对每个基因开始突变操作。
这次,使用了突变搜索算子LMA(Mutation Operator with a Local search),它用于针对社区检测问题的非常有效的突变算子。LMA的主要思想是基于Q函数的定义提出来的:

式中,f函数从所有节点的方向来评估社区检测的水平。
由于用到的模块度函数在原来基础上得到了改善,所以f函数需要进行相应改善,让它可用来解决所求问题:
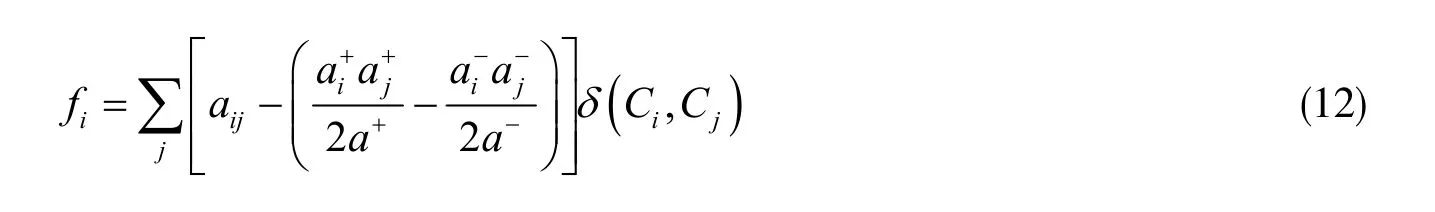
根据f函数的定义,可以在将f函数最大化并推动Q函数值点的最大化。
LMA突变算子详细操作过程如下,其中,R代表一个个体。
(1)设节点标号tb= 1。
(2)改变个体中tb号基因。设定随机数rand2与式(10)动态突变概率进行比较,若rand2<动态突变概率,那么进行(3),不然进行(6)。
(3)获取节点Vtb的相邻节点r(tb),获取r(tb)归属的社区号L,将f函数的最大值fmax置成-∞。
(4)L中的每个社区号s,若节点Vtb归属此社区,求出此时s号社区的fs,接下来对比fs与对应社区号s的fmax,若fs大于fmax,那么fmax=fs,标记fs对应社区号Imax=s。
(5)若L中的社区号全部操作结束,则节点Vtb的社区号替换为Imax,并进行(6);否则,返回(4)继续。
(6)tb=tb+1。
(7)将节点标号tb与全部节点数目n进行对比,若tb≤n,那么进行(2),不然算子终止。
3 实验结果与分析
本文测试实验采用两个基准符号网络、一个真实符号网络与多个随机生成符号对算法性能进行实验,依照NMI来评估获得的社区划分与现实中社区划分的一致程度,还有求出社区检测的准确率。测试实验中的参数设置如下:种群大小popsize设置为500,进化代数gen=50,,动态交叉概率pc=0.3+0.55/gre_num,gre_num为Greatest中历史最优解成员数。实验于Intel(R) Core(TM) i7-4510U CPU@2.00 GHz 2.60 GHz Microsoft Windows 10系统上展开,编程环境是MATLAB R2018a。
3.1 测试用的网络介绍
3.1.1 两个基准符号网络
由图4(a)呈现的基准符号网络中,实线表示正连接,虚线表示负连接,随机设定每个节点的序号。该符号网络将会被检测存在三个社区,具体检测结果为(20, 21, 10, 11, 12, 1, 2, 3, 19, 28), (8, 9, 26, 27, 17, 18),(25, 15, 22, 13, 24, 6, 23, 14, 7, 16, 5, 4)。不过,此符号网络还存在一个两社区划分结果同样可接受,(8, 19,26, 27, 17, 18, 20, 21, 10, 11, 12, 1, 2, 3, 9, 28)与(25, 15, 22, 13, 24, 6, 23, 14, 7, 16, 5, 4)。图4(b)中所示的基准符号网络和图4(a)的三个社区划分均相同。
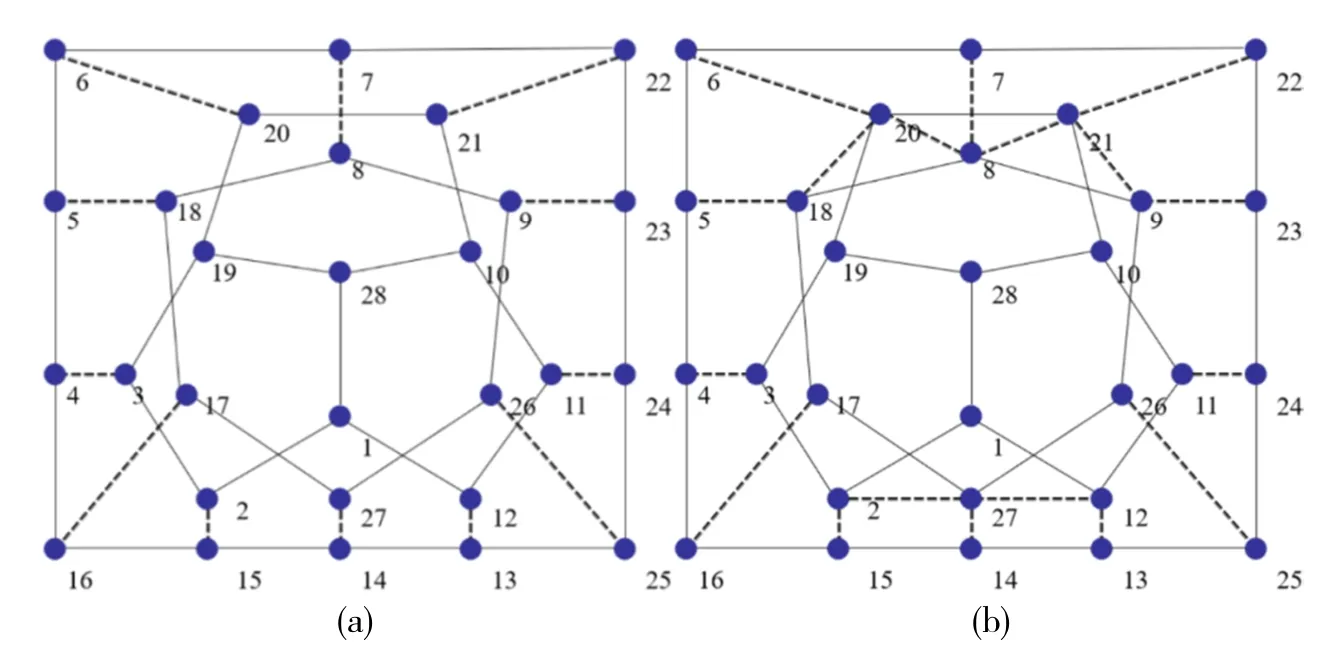
图4 基准网络拓扑图
3.1.2 真实网络Gahuku部落网络
此符号网络表示16个Gahuku-Gama部落互相的友善与对立状态,它们坐落于相对固定的区域。符号网络中的正负向边表达了它们之间的友善与敌对状态。图5呈现Gahuku部落的连接网络。

图5 Gahuku部落的连接网络
3.1.3 随机符号网络
为更准确的检验改善后的算法性能,根据文献[8]构造了含有参数的随机符号网络SG(C,N[n1,n2,…,nC],PN,P-,P+)的生成函数,其中,C代表社区的数目;N[n1,n2,…,nC]代表每个社区的节点个数;PN代表社区之间负向连接与社区内正向连接总数之比;P-代表社区内部负向连接与社区内部正向连接总数之比;P+代表社区之间正向连接与社区之间负向连接总数之比。SG(C,N[n1,n2,…,nC],PN,P-,P+)产生的具体步骤:①根据设定参数,将产生C个社区,且均在以起始节点数是5的完全连通图为基础持续的增添新点,新增添的点将和之前存在节点中5个任意节点进行正向连线,由此构造出类似无标度的网络;②按概率PN持续的往各个社区外部增添负连接;③按概率P-与概率P+持续往社区里增添负连接和社区外增添正连接。本实验对SG(3,N[30,30,40],PN,P-,P+)进行了测试。
3.2 实验结果
3.2.1 基准测试网络上的实验结果
从表1中可知,3个测试符号网络均可以达到NMI = 1,说明改善后得到的符号网络社区检测结果完全符合现实情况,由此证明了本算法是有效的。
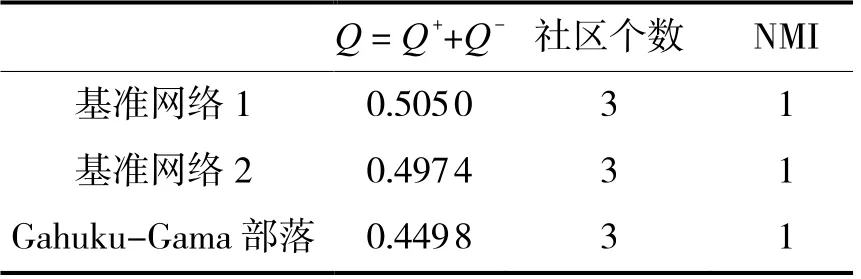
表1 本文算法对3个测试符号网络的测试数据
对于2个基准网络,基准网络1和2,运行获得的检测结果如图6所示,将会精准获得3个社区的划分,图中黑白灰色的圆形表示各个社区节点。结果为:社区1(1, 19,11, 3, 28, 12, 2, 20, 21, 10),社区2(18, 27, 17, 9, 8, 26)和社区3(24, 25, 14, 13, 5, 7, 16, 22, 6, 23, 15, 4),这个划分对应得到的NMI值是1。
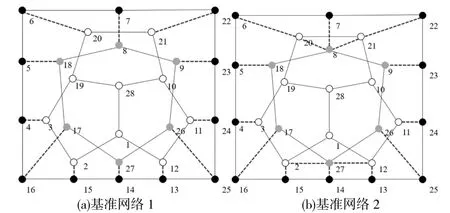
图6 本文算法检测到的两个基准网络的社区图
3.2.2 真实网络上的结果
真实符号网络改善后得到的网络社区检测结果如图7所示,图中黑白灰色的圆形表示各个社区的节点。获得的社区结构与原有社区检测情况相同。
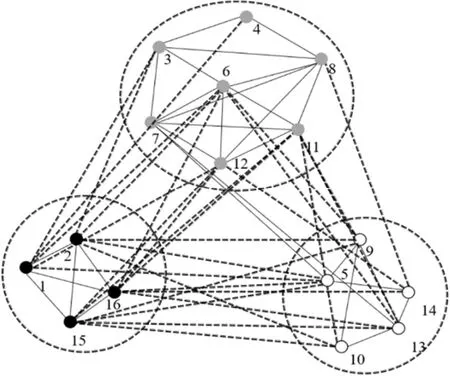
图7 Gahuku-Gama部落的社区划分结果
3.2.3 随机网络的实验结果
为更准确的检验改善后的结果性能,使用随机产生的符号网络来测试,以测试改善和引入的策略是否有效。通过优化由多目标通过权重系数变换法得到的单目标函数Q(Q=Q++Q-)来发现随机符号网络里的社区划分,对比算法来自文献[12]。
(1)参数PN的影响。对随机符号网络SG(3,N[30,30,40],PN, 0, 0)进行测试,PN的取值范围为0.2~1.0,间隔为0.2。实验结果如表2所示,由表2能够明确获知,改进前后均能达到NMI = 1,说明改进前后得到的社区检测结果等同于现实情况,并且获知PN的持续提升,即符号网络中社区外部的负向连接数目持续提升,改进前后的Q均有下降,但均没有影响到最后的检测结果。
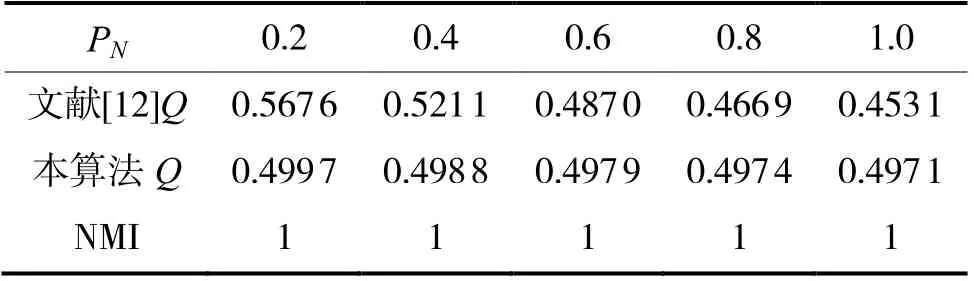
表2 实验对比结果
(2)参数P+的影响。对随机符号网络SG(3,N[30,30,40], 0.2, 0,P+)进行测试,P+的取值范围为0.2~1.0,间隔为0.2。实验结果如表3所示,由表3能够明确获知,当P+= 0.2时,NMI = 1,说明改进前后得到的社区检测结果等同于现实情况。并且P+的持续提升,即社区内的正向边数目持续提升,改进前的NMI持续减小,说明P+的变化,对改善前的算法的Q干扰逐渐增加,而改善后的Q虽说也有逐渐下降趋势,但Q下降的较为缓慢,还不足对它找到最优划分的过程产生重大影响。
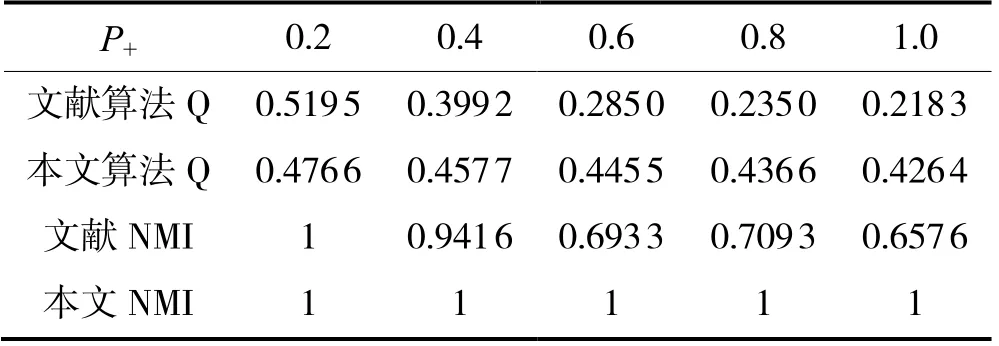
表3 实验对比结果
(3)参数P+和P-的影响。对随机符号网络SG(3, N[30,30,40], 0.2,P-,P+)进行测试,于符号网络SG(3,N[30,30,40], 0.2, 0,P+)社区内以概率P-持续连接负向关系,此次试验,P+的值域为0.1~0.3,P-的值域为0.1~0.5,间隔均为0.1。实验结果如表4所示,由表4能够明确获知,若P+,P-持续升高,改善前后的Q值均呈现出持续下降,但改善后NMI值不会出现改善前NMI值会持续降低。当P+与P-相对不高时,改善前获得的社区划分较为相似于现实情况,所以其NMI值偏高;相比改进后得到Q值的下降没有之前那么剧烈,而且仍然可以找到最优划分,说明各增添的策略和改进后的算子增强了算法整体的稳定性。
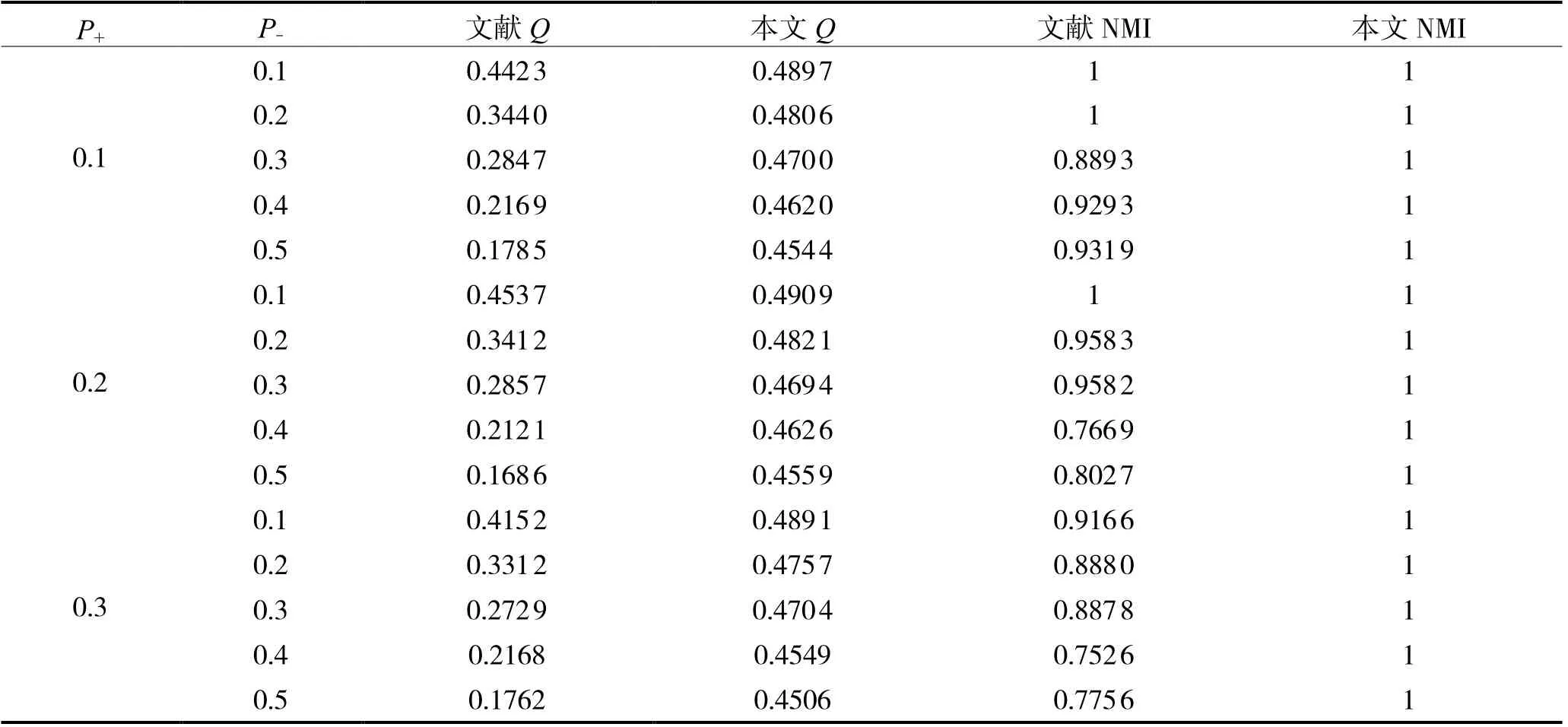
表4 实验对比结果
4 结论
在符号网络中找出这些社区结构有助于人们更加准确地获知网络整体结构、精准地推断出网络中各节点之间的联系和某些节点的共同特性。本文设计了一种基于进化计算的复杂网络社区检测算法,实验结果验证了其有效性。测试实验所测试用的符号网络节点数不多,而在现实情况,更多还是数百甚至上千万个点构成的大型符号网络,届时所用算法的时间空间复杂度是必须要优化升级的。

