基于运动学的机器人脚轮数学模型构建与仿真

周烨

（常州刘国钧高等职业技术学校，江苏 常州 213000）

1 概述

数学及数学工具如MATLAB 现已渗透到各个工程领域并开展了广泛深入的应用，正是这些应用的广泛和深入推广，推动了工程领域的高速发展。在工程领域，全向移动机器人具有平面内三个自由度（即具有全向移动性），适合在狭小的工作空间内移动[1]。经查阅文献，国内对主动脚轮研究甚少，仅在文献[2]中进行了研究，其研究方向侧重于控制算法研究[2]。同时，文献[3]表明主动脚轮是全向移动机器人的理想行走机构。因此，本文对机器人脚轮展开研究，利用脚轮基本的几何和运动关系，构建并推导了脚轮速度的数学关系表达式及运动学数学模型，同时进一步采用数学仿真工具MATLAB 对其进行仿真计算，获得了该脚轮的运动学解，验证了本文所构建的数学模型的正确性，为机器人脚轮及相近领域提供一定的分析参考。

2 移动机器人的运动学分析

2.1 移动机器人的结构简述

机器人主动脚轮具有驱动能力，主动脚轮具有驱动电机和转向电机两个电机同时驱动。其结构有驱动电机、齿轮、皮带等。

2.2 机器人脚轮滑动的数学关系表达

2.3 脚轮运动学模型建立

根据两脚轮的几何关系，同时对角度以时间进行求导，得出两轮子作用到移动机器人几何中心的速度为：

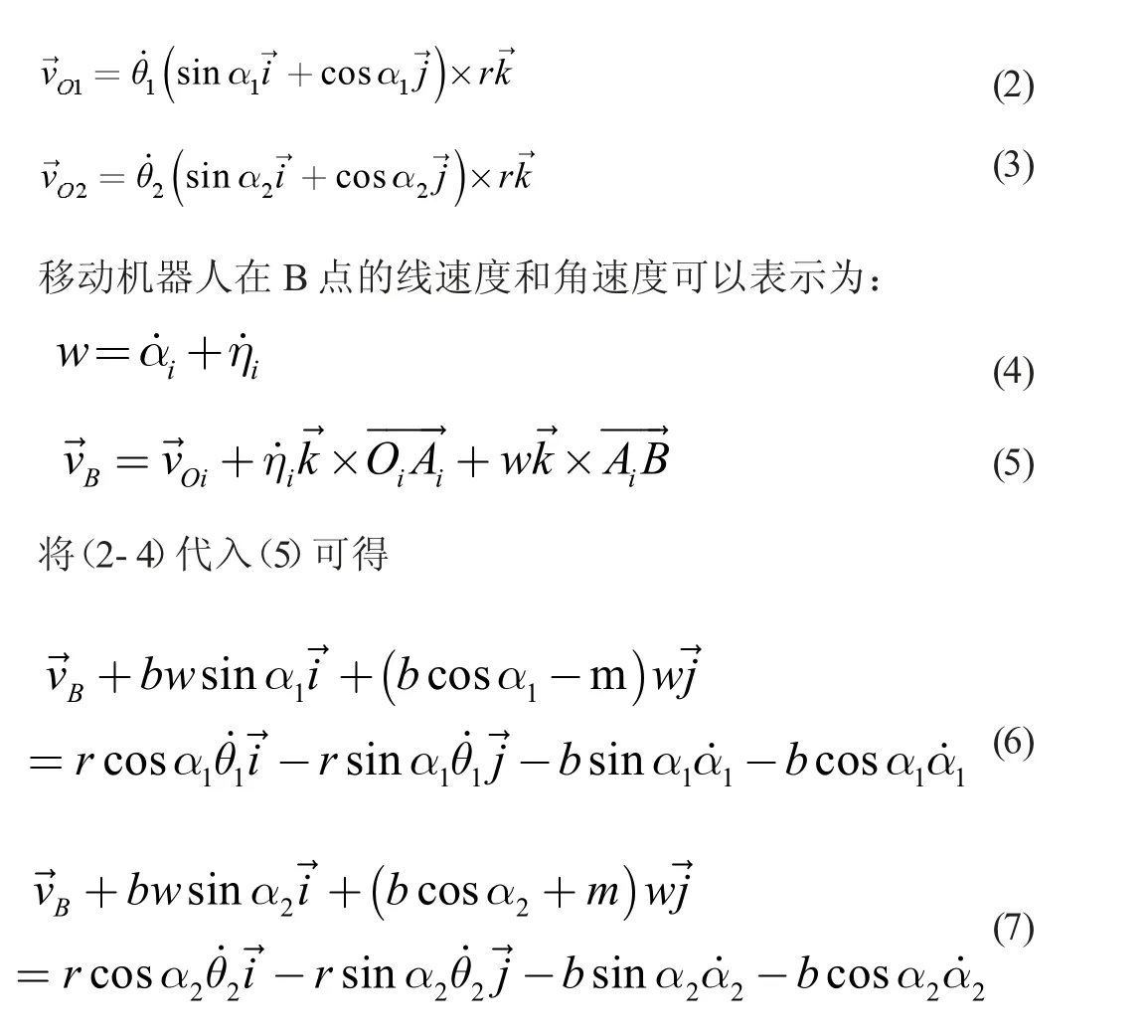
整理成矩阵形式脚轮1 的运动学模型为：

3 仿真求解与轨迹规划

3.1 软件仿真求解结果

采用数学工具MATLAB 软件对上述模型进行求解，将模型的尺寸参数、电机转速参数作为输入条件，其中结构参数为：m=692.82mm，r=b=50mm。在软件中获取机器人进行原地转向1s后，得到机器人的各运动关节数据如图2 所示。

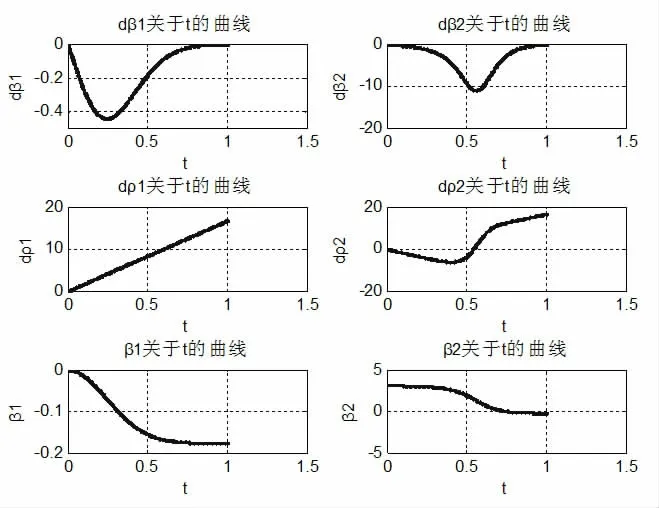
图2 脚轮软件求解结果曲线

3.2 移动机器人脚轮轨迹规划

轨迹规划是移动机器人进行运动控制的关键步骤，是分析计算的目的和意义所在。轨迹规划发方法很多，目前普遍的是多项式法。由于采用五次多项式进行插值能保证位置、速度、加速度以及加价速度的曲线平滑，因此本文采用五次多项式法进行轨迹规划。在XY 平面用五次样条曲线对移动机器人进行轨迹规划后得到的位置（P），速度（V），加速度（a）曲线值如图3 所示。

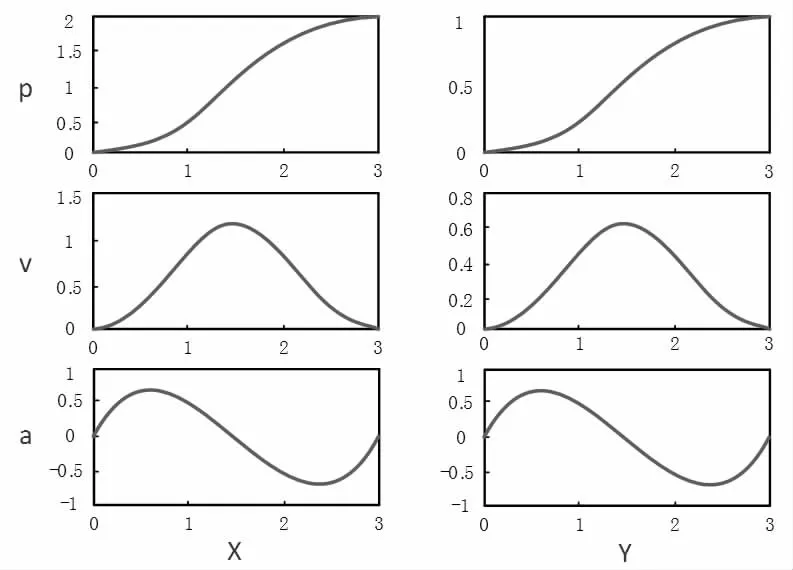
图3 机器人的位置、速度、加速度曲线图

从仿真结果来看：对于移动机器人进行速度规划，令移动机器人的运动轨迹为一个矩形；移动机器人以0.25m/s2的加速度加速2s 后，以0.5m/s 的速度匀速行驶4s，最终以0.25m/s2的加速度减速到静止；移动机器人以-0.25m/s2的加速度加速2s 后，以0.5m/s 的速度实现倒行，最终以0.25m/s2的加速度减速到停止；移动机器人以0.25m/s2的加速度加速2s 后，实现以0.5m/s的速度匀速侧向移动4s，最终以0.25m/s2的加速度减速到静止。移动机器人的运动仿真与预期规划好的运动轨迹完全吻合，文中所建立的移动机器人的运动学模型合理。

4 结论

采用数学及其数学工具，针对一种机器人脚轮展开分析，利用脚轮基本的几何和运动关系构建并推导了脚轮速度的数学关系表达式及运动学数学模型，进一步对其仿真求解验证了模型的正确性；并在此基础上进一步采用五次多项式进行了轨迹规划，获得了较好的控制目标，能够为机器人脚轮的设计计算提供一定参考和借鉴。