本构模型对GH4169缺口件蠕变变形响应计算结果的影响
胡贤明, 嵇大伟, 庄书颖, 胡绪腾
(南京航空航天大学 能源与动力学院,南京 210016)
在持续载荷作用下,高温构件经过一定的时间会发生不可恢复的蠕变变形,经过足够长的时间后会发生断裂失效,在恒定载荷下直至失效所经历的时间称为构件的持久寿命(或称应力断裂寿命)。对于航空发动机的高温构件而言,在设计时需控制其应力水平,使其持久寿命满足要求[1]。此外,还需对结构的蠕变变形进行限制,防止变形过大导致转静子碰摩和影响发动机结构装拆[1-2]。
目前,对金属材料的高温蠕变变形以及持久性能方面内容已进行了大量研究,发展出了不同的预测方法[3-10]。叶文明等[3]和马晓健[4]采用θ参数法蠕变本构模型,通过对TC11钛合金在500 ℃下的蠕变/持久实验进行分析,建立了基于大变形蠕变分析的持久寿命预测方法,较准确地预测缺口试件的高温蠕变响应和持久寿命,预测结果与实验结果的误差在 ± 40%以内,该方法的预测精度优于一些国外文献提出的基于关键点断裂应变[5]、缺口净截面平均有效应力[6-7]以及骨点应力[8-10]的小变形有限元分析的寿命预测方法。王延荣等[11-13]分析了不同蠕变模型的差别,发现一般的蠕变模型只能描述蠕变前两个阶段(初始阶段和稳定阶段)的变形。构件在其使用寿命内几乎都处于蠕变前两个阶段,但同时也需要能够描述第三阶段(加速阶段)蠕变变形的模型,以便判断构件是否处于比较危险的蠕变加速阶段;因此提出了一种归一化参数的三阶段蠕变模型,并对高温材料涡轮盘和定向结晶材料涡轮叶片结构进行了蠕变变形及应力松弛效应计算分析,分析结果较为合理。总体来看,在复杂应力状态下,准确预测高温构件的蠕变变形和持久寿命仍是一个较为困难的问题。
由于实际构件在蠕变失效时已累积较大变形,因此在进行有限元分析时不能忽略因变形导致的结构尺寸和形状的改变。GH4169合金具有良好的综合性能,目前被广泛用于航空发动机高温部件中[14-15]。GH4169合金长时间工作最高温度为650 ℃,开展该温度下蠕变实验和失效规律研究具有较为重要的意义。本工作基于大变形有限元方法,采用弹塑性耦合蠕变分析对GH4169光滑和缺口试件的高温蠕变变形响应和持久寿命进行有限元计算,分析蠕变本构模型对光滑和缺口试件蠕变变形响应和持久寿命计算结果的影响。
1 材料与实验方案
实验材料为直接时效GH4169合金。
设计如图1所示的光滑平板高温拉伸试件和3种双边缺口平板高温拉伸试件,缺口半径R分别为1 mm、5 mm和20 mm,应力集中系数分别为2.8、1.5和1.1,拉伸实验温度为650 ℃。
光滑和缺口蠕变试件设计方案如图2所示,蠕变实验方案见表1,施加的载荷根据平板试件最小截面上所承受的名义应力确定,实验温度650 ℃。
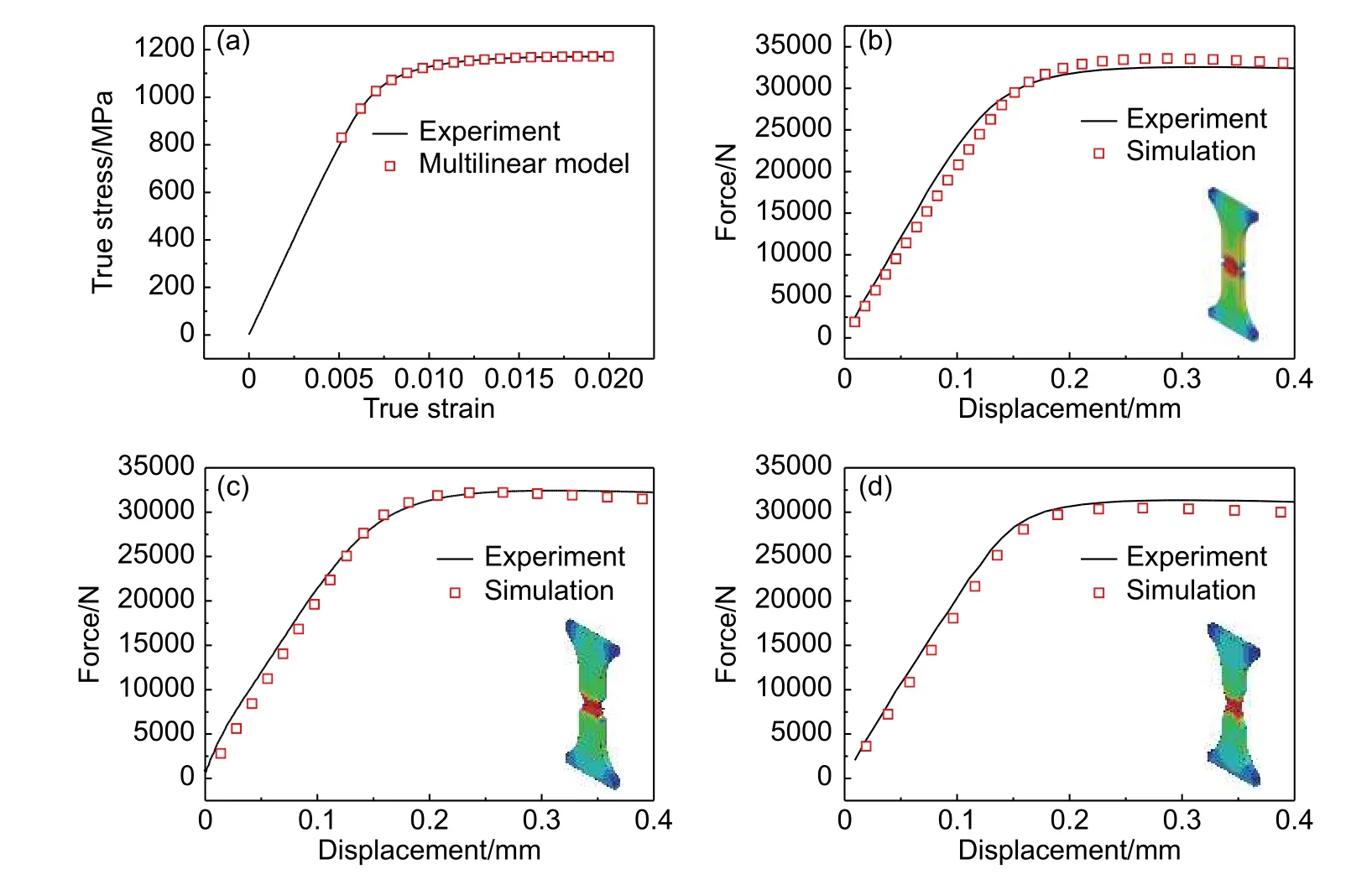
图 3 GH4169合金拉伸试件 (a)光滑平板;(b)R1双边缺口平板;(c)R5双边缺口平板;(d)R20双边缺口平板Fig. 3 Tensile specimens of GH4169 alloy (a)smooth plate;(b)R1 double notched plate;(c)R5 double notched plate;(d)R20 double notched plate
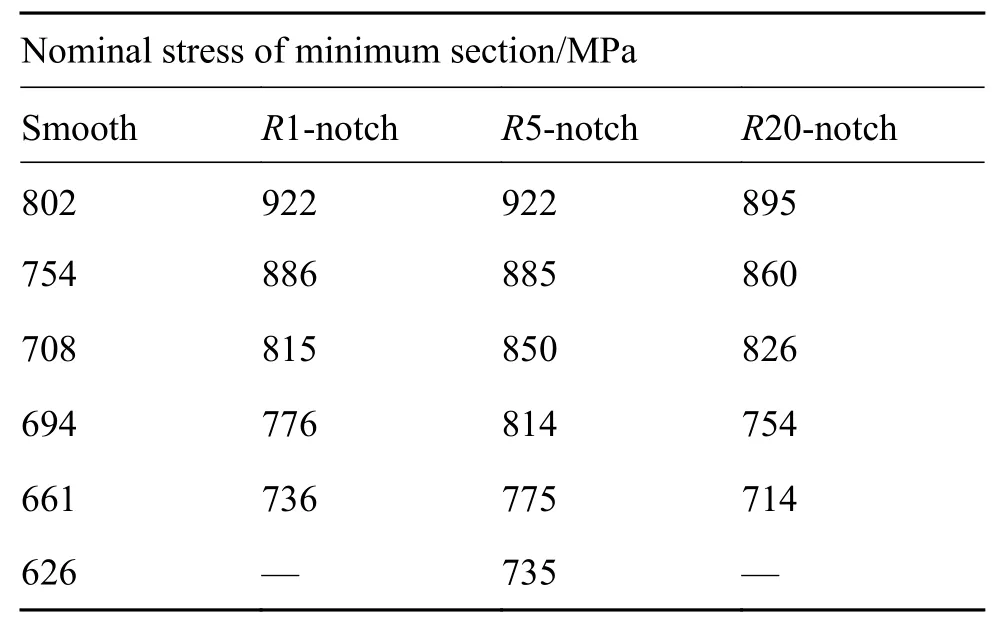
表 1 GH4169合金平板试件高温蠕变实验方案Table 1 High temperature creep test scheme of GH4169 alloy plate specimen
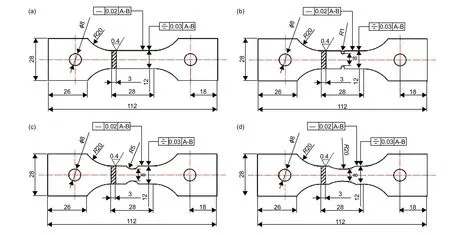
图 1 GH4169合金平板拉伸试件 (a)光滑平板;(b)R1双边缺口平板;(c)R5双边缺口平板;(d)R20双边缺口平板Fig. 1 Tensile specimens of GH4169 alloy (a)smooth plate;(b)R1 double notched plate;(c)R5 double notched plate;(d)R20 double notched plate
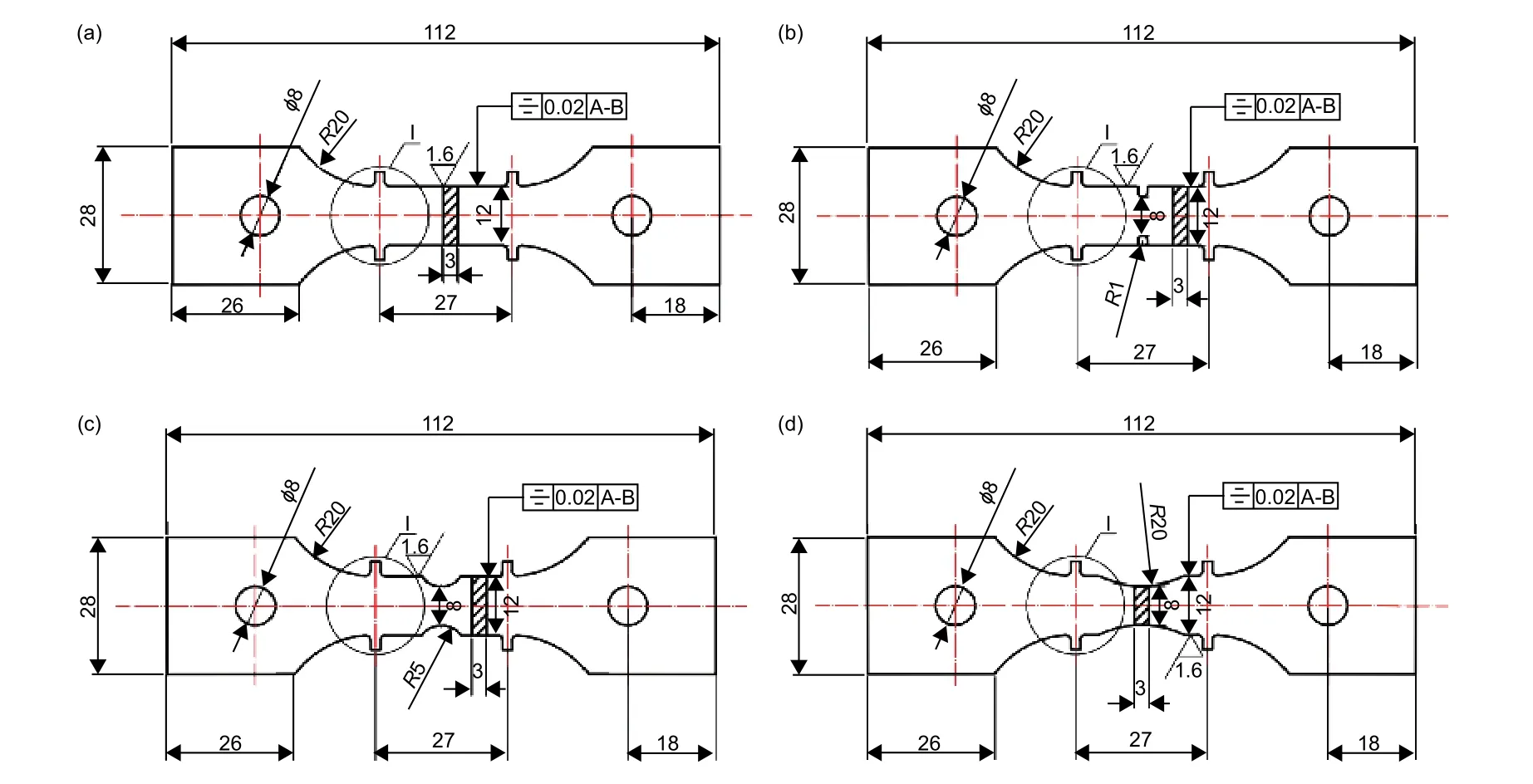
图 2 GH4169合金平板蠕变试件 (a)光滑平板;(b)R1双边缺口平板;(c)R5双边缺口平板;(d)R20双边缺口平板Fig. 2 Creep specimens of GH4169 alloy (a)smooth plate;(b)R1 double notched plate;(c)R5 double notched plate;(d)R20 double notched plate
2 GH4169合金弹塑性和蠕变本构模型
材料的弹塑性和蠕变本构模型均采用真应力、真应变数据来建立。弹性变形采用广义Hooke定律来描述。塑性变形采用多线性各向同性硬化模型来描述。短时弹塑性变形的真应力、真应变与工程应力、工程应变之间的转换关系如下:

式中:σ为真应力;ε为真应变;σe为 工程应力;εe为工程应变。
蠕变变形阶段的真应力、真应变与工程应力和工程应变之间的转换关系如下:
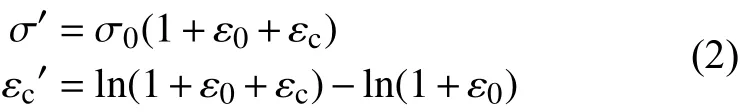
式中:σ′为 真应力;εc′为 真蠕变应变;ε0为初始加载弹塑性应变;εc为 工程蠕变应变。
本工作采取三种能描述蠕变三阶段变形曲线的本构模型来建模,一种是Wilshire等[16-17]提出的θ参数模型,单轴应力下其公式为:
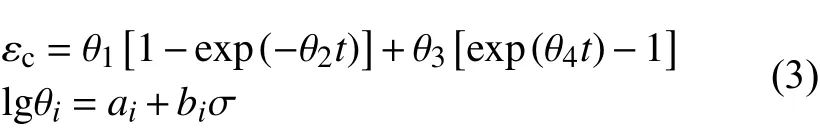
式中:εc为 工程蠕变应变;t为 时间;ai、bi(i= 1、2、3、4)为待定参数。第二种是Ye等[18]提出的修正蠕变本构模型,单轴应力下该模型的表达式为:
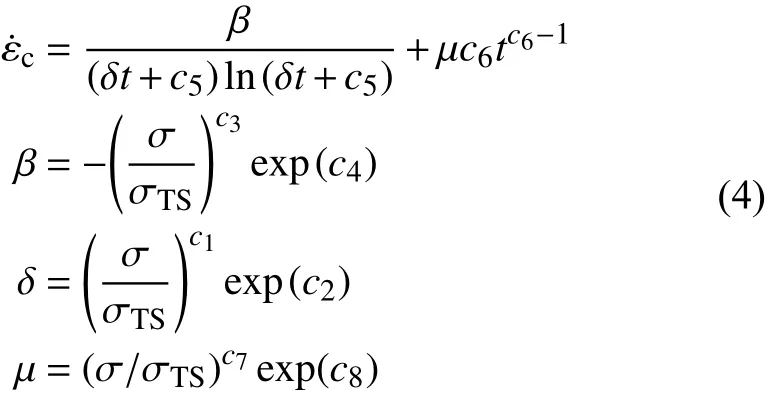
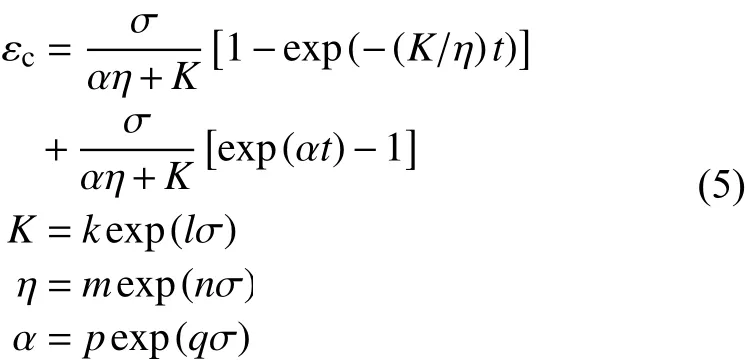
式中:k、l、m、n、p、q为待定参数。
3 基于大变形有限元分析的弹塑性和蠕变响应计算
3.1 基于大变形有限元分析的弹塑性响应计算
由实验得到的GH4169合金平板件650 ℃拉伸数据如图3黑色实线所示。根据式(1),对材料光滑拉伸数据进行真应力-真应变转换,由于本构模型的拟合只能采用最大应力之前的数据,因此图3 (a)中只给出了试件从加载到最大应力之间的真应力-真应变曲线,由弹性段可拟合得到材料的弹性模量为161.2 GPa,泊松比为0.3,并基于塑性段获取多线性各向同性硬化塑性本构模型参数来对试件的弹塑性变形响应进行有限元计算。
根据试件的形状在有限元软件中进行三维建模计算,三种缺口试件的弹塑性响应大变形有限元计算结果如图3(b)~(d)所示,由图可知,实验和有限元计算得到的载荷-位移曲线十分贴合,缺口试件的弹塑性变形均得到较好的预测。根据有限元计算的最大载荷可以得到缺口试件的极限强度,即名义抗拉强度,三种缺口试件计算得到的极限强度分别为:1399 MPa(R1缺口平板)、1342 MPa(R5缺口平板)以及1270 MPa(R20缺口平板),与实验值之间的误差分别为:+3.0%、+0.65%以及-2.8%,相对误差均在 ± 3%以内。总之,基于大变形有限元分析方法,三种缺口平板试件的弹塑性变形和极限强度都得到较好的预测。
3.2 基于大变形有限元分析的蠕变响应计算
由实验得到GH4169合金光滑试件650 ℃下的蠕变数据,根据式(2)对工程应力和工程蠕变应变进行转换,转换成真实应力和真实蠕变应变,并采用θ参数法、修正蠕变模型以及Batsoulas模型对转换后的数据进行拟合,拟合结果如图4所示,得到的本构模型的参数见表2~表4。将这三种蠕变本构模型分别和商用有限元软件进行编译链接,形成可执行的用户子程序,在软件中进行调用即可使用这三种模型完成所需的蠕变响应计算。

表 2 θ参数法模型拟合参数值Table 2 Fitting parameter values of θ-projection model

表 3 修正蠕变模型拟合参数值Table 3 Fitting parameter values of modified creep model
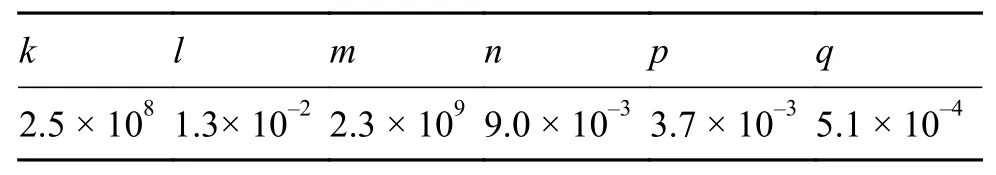
表 4 Batsoulas模型拟合参数值Table 4 Fitting parameter values of Batsoulas model
图5 给出了GH4169合金光滑平板和3种缺口平板高温蠕变试件的有限元模型。由于试件为带厚度的板件,需建立三维单元模型,因此可采用Solid 186单元进行分网建模。根据实验条件,在所建立模型底端的面上施加固支约束,在另一端面的上方建立一个刚性节点与端面上的节点进行耦合,并在刚性节点上施加对应于实验的载荷,目的是为了将平板一端的力集中于一点,使有限元计算过程更加接近真实实验过程。
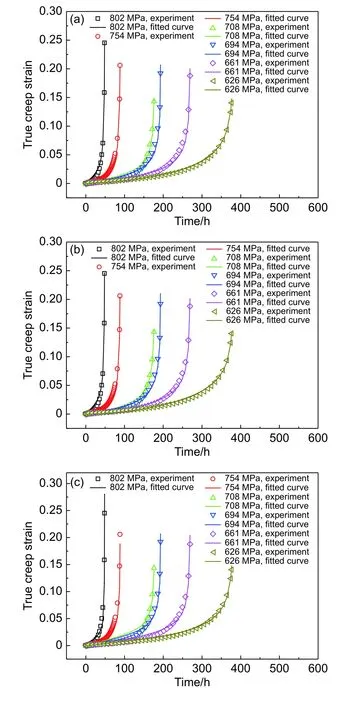
图 4 GH4169合金光滑试件蠕变数据拟合结果 (a)θ参数法;(b)修正蠕变模型;(c)Batsoulas模型Fig. 4 Creep data fitting results of GH4169 alloy smooth specimen (a)θ-projection model;(b)modified creep model;(c)Batsoulas model
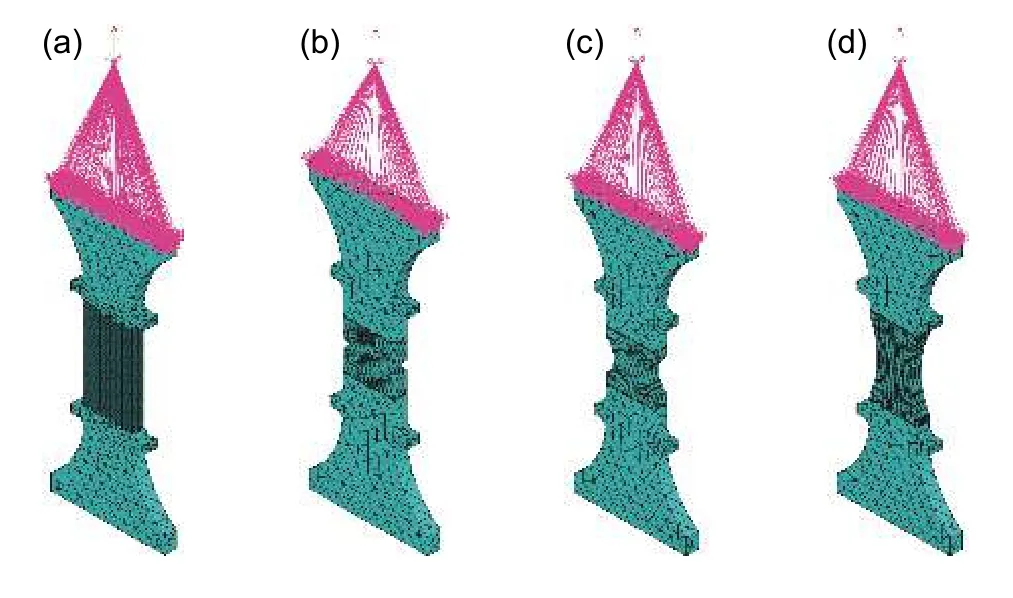
图 5 GH4169合金平板蠕变试件有限元模型 (a)光滑平板;(b)R1缺口平板;c)R5缺口平板;(d)R20缺口平板Fig. 5 Plate tensile specimens of GH4169 alloy (a)smooth plate;(b)R1 double notched plate;(c)R5 double notched plate;(d)R20 double notched plate
基于大变形有限元分析的弹塑性耦合蠕变计算步骤为:(1)计算弹塑性加载过程,设置加载结束时间为10-8h,并打开大变形计算选项;(2)计算后继恒定载荷下的蠕变过程,打开率相关的选项,分段设置时间增量步,以10倍时间间隔为基础,可避免蠕变计算不收敛的问题,终止分析时间的最大值为该应力条件下的蠕变寿命,分析子步可根据计算模型的几何尺寸进行调整,其取值在100~500 h左右。
由上述建立的有限元模型,在完成弹塑性加载和蠕变保载计算过程后,通过后处理所建模型上下凸台对应节点位置的变形位移数据,减去初始弹塑性变形位移值后,即可得到所需的蠕变变形-时间曲线数据。GH4169合金光滑平板试件高温蠕变有限元计算结果如图6所示,给出了光滑试件在三种不同蠕变本构模型大变形有限元计算下的蠕变响应计算结果。从图6可以看出,采用θ参数法模型计算出的光滑试件蠕变断裂变形值和蠕变断裂时间与实验值最为接近,但蠕变各阶段的变形曲线与实验曲线存在一定差距,蠕变前两个阶段的变形计算值偏大;修正蠕变模型计算出的光滑试件蠕变断裂变形值和蠕变断裂时间与实验值相差最大,但其描述蠕变前两个阶段的曲线效果最好;而对于Batsoulas模型而言,其对于光滑试件的描述效果介于前两种模型之间,且也能较好描述前两个阶段的蠕变变形。
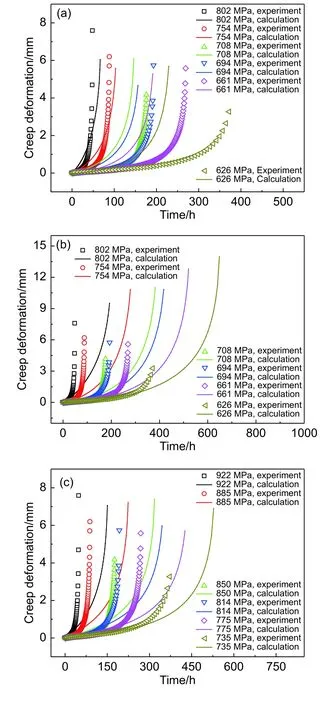
图 6 光滑平板大变形蠕变响应计算结果 (a)θ参数法;(b)修正蠕变模型;(c)Batsoulas模型Fig. 6 Calculation results of large deformation creep response of smooth specimen (a)θ-projection model;(b)modified creep model;(c)Batsoulas model
图7 ~图9给出了缺口试件在三种不同蠕变本构模型大变形有限元计算下的蠕变响应计算结果。从图7~图9可以看出,在大变形计算下,θ参数法模型计算出的缺口试件蠕变持久寿命与实验值最为接近,而蠕变断裂变形值与实验结果相差较大,且差值随着缺口半径变小而增大,蠕变前两个阶段的变形计算值与实验值相比普遍偏大;同样,修正蠕变模型计算出的缺口试件蠕变断裂变形值和蠕变断裂寿命与实验值相差最大,但其描述蠕变前两个阶段的曲线效果仍是最好;而对于Batsoulas模型而言,其对于缺口试件的变形描述效果介于前两种模型之间,且也能较好描述前两个阶段的蠕变变形。
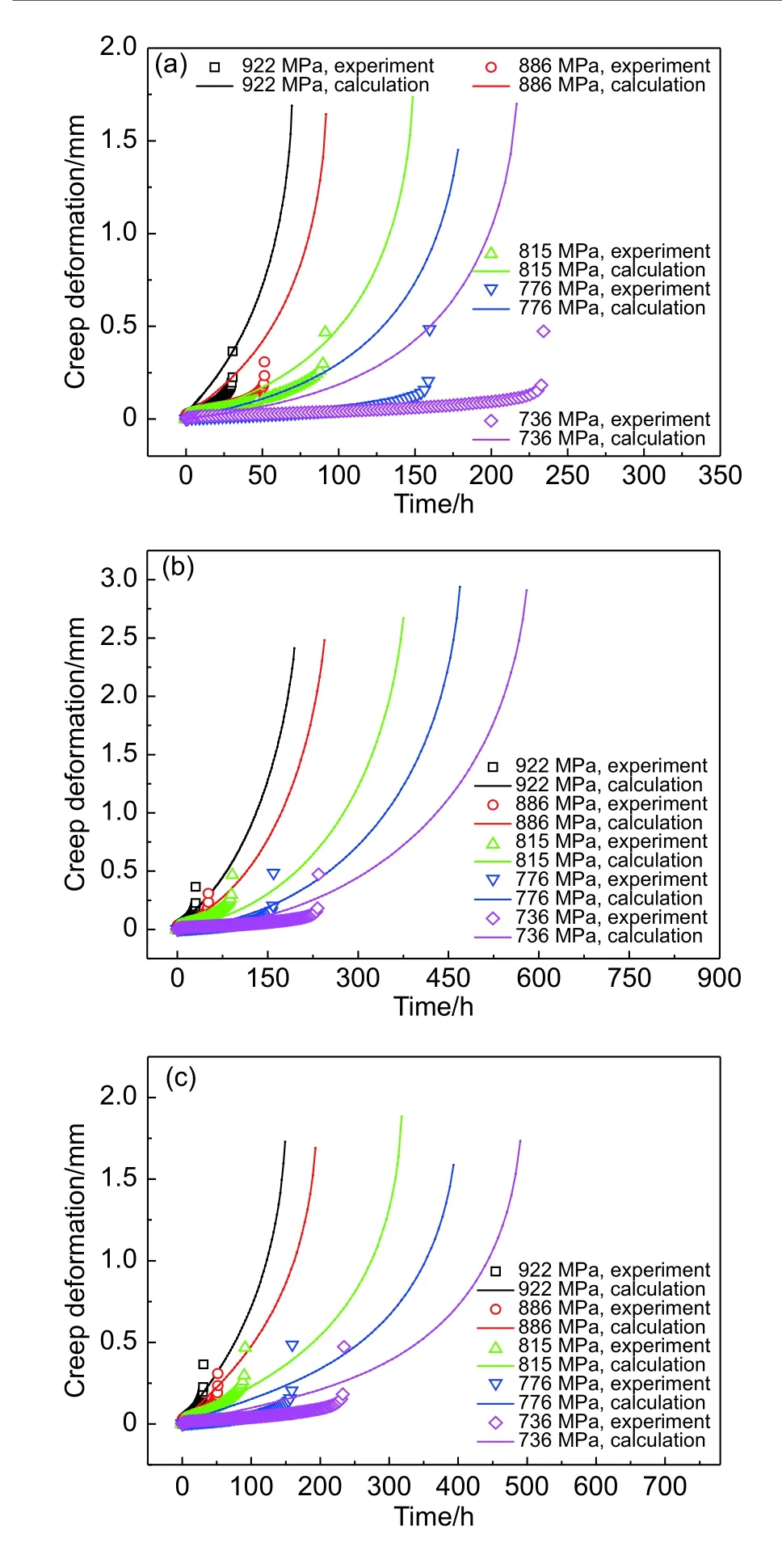
图 7 R1缺口平板大变形蠕变响应预测结果 (a)θ参数法;(b)修正蠕变模型;(c)Batsoulas模型Fig. 7 Prediction results of large deformation creep response of R1 notched specimen (a)θ-projection model;(b)modified creep model;(c)Batsoulas model
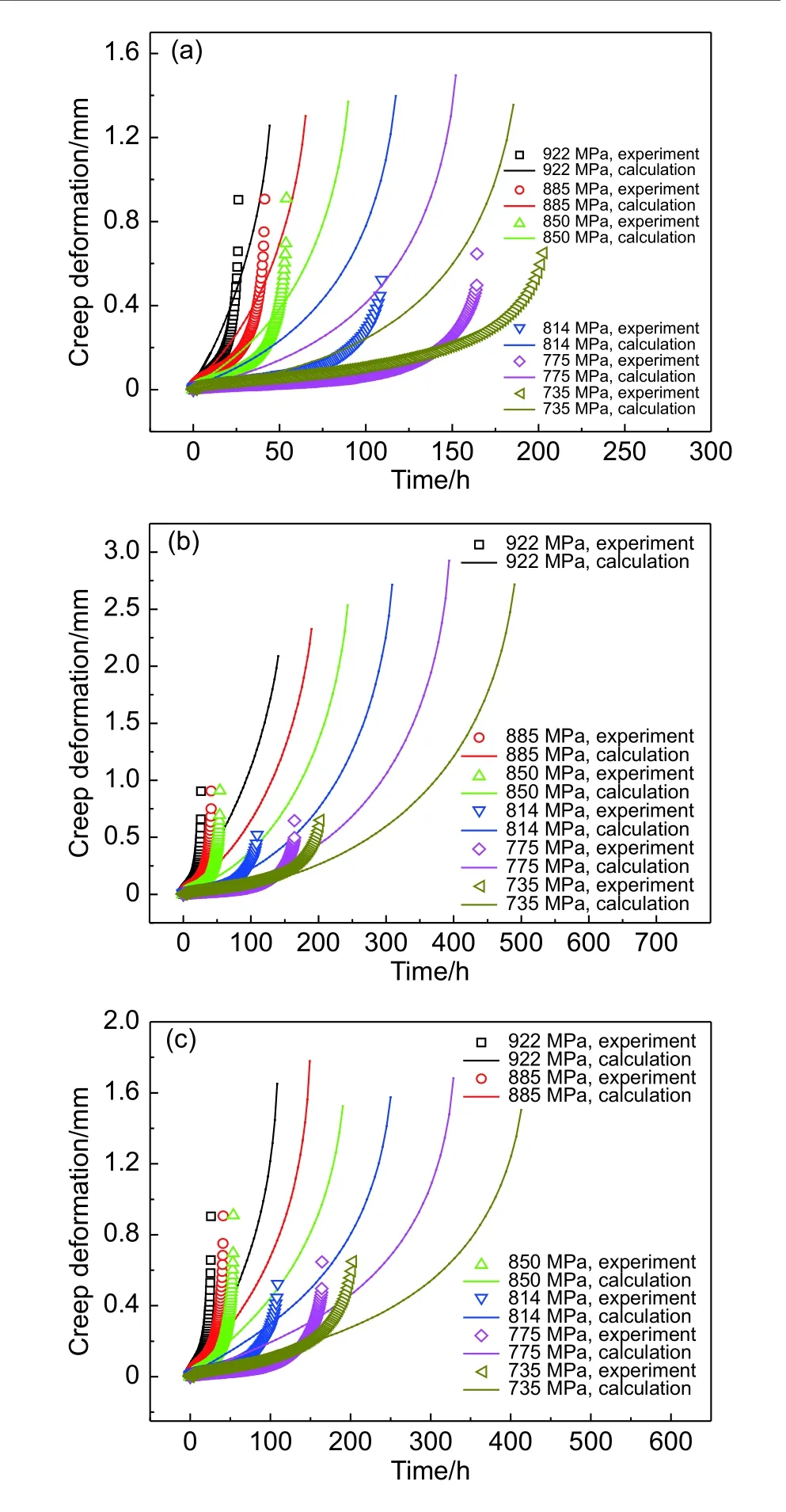
图 8 R5缺口平板大变形蠕变响应预测结果 (a)θ参数法;(b)修正蠕变模型;(c)Batsoulas模型Fig. 8 Prediction results of large deformation creep response of R5 notched specimen (a)θ-projection model;(b)modified creep model;(c)Batsoulas model
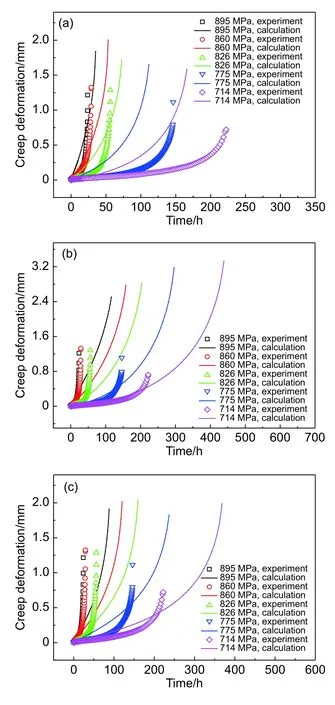
图 9 R20缺口平板大变形蠕变响应预测结果 (a)θ参数法;(b)修正蠕变模型;(c)Batsoulas模型Fig. 9 Prediction results of large deformation creep response of R20 notched specimen (a)θ-projection model;(b)modified creep model;(c)Batsoulas model
总体来看,三种蠕变模型对于缺口平板试件在大变形有限元分析下的蠕变响应预测效果不一,θ参数法对于缺口持久寿命的预测较为准确,而蠕变变形预测效果较差;修正蠕变模型对于缺口持久寿命的预测较差,而蠕变前两个阶段的变形预测效果较好;而Batsoulas模型在大变形有限元分析下的蠕变响应预测效果介于前两种模型之间。同时,三种模型预测的蠕变断裂变形值与实验值相比均偏大,且差值随着缺口半径变小而增大。
3.3 基于大变形有限元分析的蠕变/持久寿命预测分析
上文已采用大变形有限元分析方法计算了光滑和缺口试件在高温下的整体变形响应曲线,随计算时间的增加,试件变形量将逐渐增大,其内部危险部位变形逐渐累积,当整体变形响应因其局部蠕变变形累积到第三阶段时急剧增大,有限元计算过程将无法收敛而停止,此时可认为试件发生持久断裂破坏[3]。因此,上文计算获得的蠕变断裂时间即为基于大变形有限元方法预测的蠕变/持久寿命。
为了更加直观地对比三种蠕变本构模型对试件蠕变/持久寿命的预测效果,采用寿命分散带图形进行描述,如图10所示。对于θ参数法模型而言,采用基于大变形有限元分析的蠕变/持久寿命预测方法可以较准确地预测光滑试件的蠕变寿命及三种缺口试件的持久寿命,预测误差基本在 ±2倍分散带以内,个别数据点在+2.5倍以内;修正蠕变模型对于蠕变/持久寿命预测效果较差,预测误差基本在+7倍分散带以内,寿命预测偏大;Batsoulas模型蠕变/持久寿命预测结果同样偏大,预测误差基本在+5倍分散带以内。该结论进一步说明,在使用大变形有限元方法预测高温构件蠕变响应时,采用θ参数法模型可较为准确地预测构件的持久寿命,而采用Batsoulas模型和修正蠕变模型可较为准确地预测蠕变前两个阶段的变形。
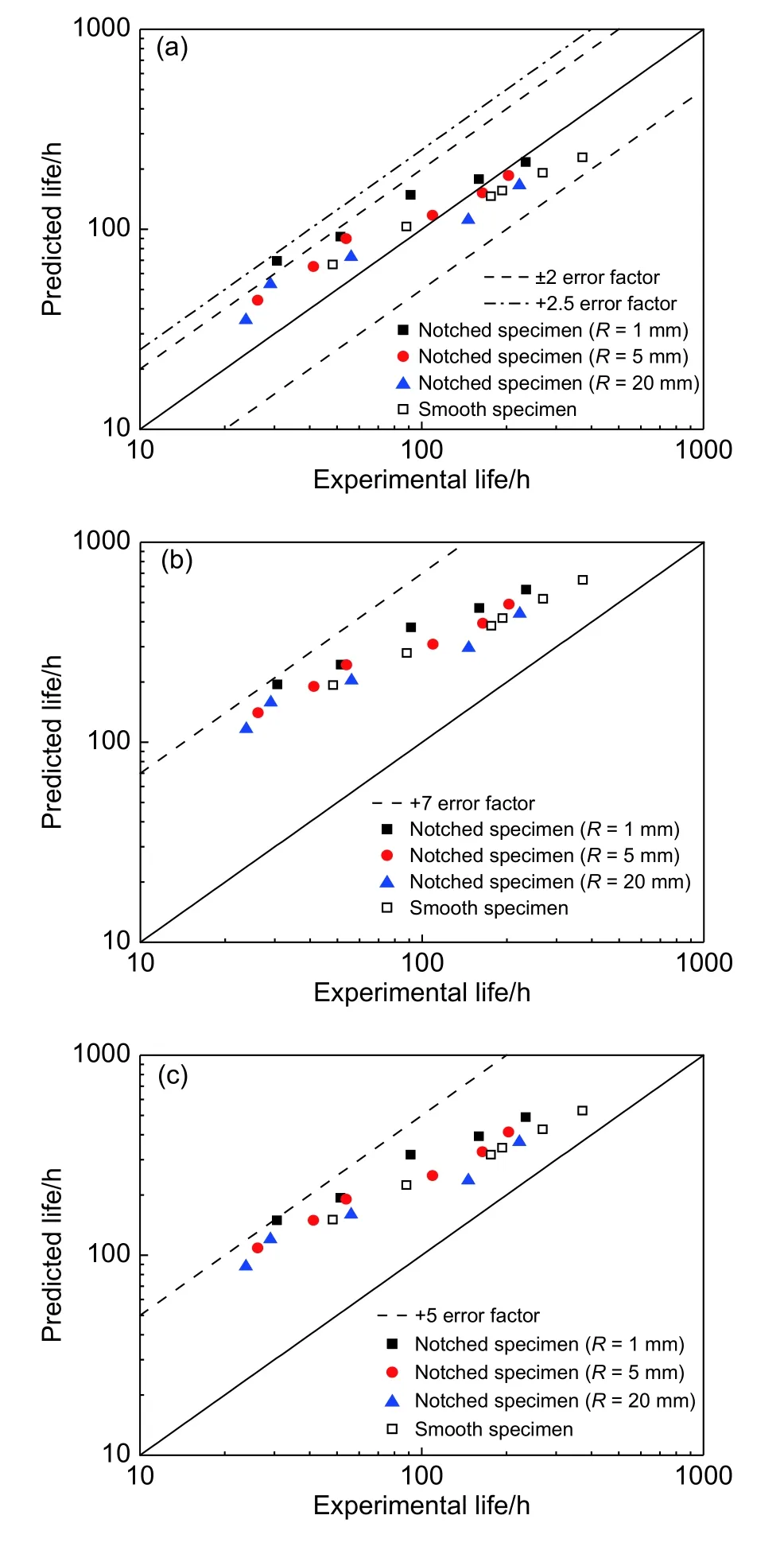
图 10 大变形蠕变/持久寿命预测结果 (a)θ参数法;(b)修正蠕变模型;(c)Batsoulas模型Fig. 10 Prediction results of large deformation creep rupture life (a)θ-projection model;(b)modified creep model;(c)Batsoulas model
4 结论
(1)基于大变形有限元分析的方法能较好地预测弹塑性变形响应,三种缺口平板试件的弹塑性变形和极限强度都得到良好的预测,极限强度预测误差均在 ± 3%以内。
(2)三种蠕变本构模型对于缺口平板试件在大变形有限元分析下的蠕变响应预测效果不一,θ参数法对于缺口持久寿命的预测较为准确,而蠕变变形预测效果较差;修正蠕变模型对于缺口持久寿命的预测较差,而蠕变前两个阶段的变形预测效果较好;而Batsoulas模型在大变形有限元分析下的蠕变响应预测效果介于前两种模型之间。
(3)基于大变形有限元分析的蠕变/持久寿命预测方法,θ参数法模型可以较为准确地预测光滑试件的蠕变寿命及三种缺口试件的持久寿命,预测误差基本在 ± 2倍分散带以内,个别数据点在+2.5倍以内;修正蠕变模型对于蠕变/持久寿命预测效果较差,预测误差基本在+7倍分散带以内,寿命预测偏大;Batsoulas模型蠕变/持久寿命预测结果同样偏大,预测误差基本在+5倍分散带以内。

