基于应力修正的2195铝锂合金本构模型及热加工性能
赵一帆, 吴文科, 何国爱,3*, 王 强
(1.中南大学 轻合金研究院,长沙 410083;2.中南大学 高性能复杂制造国家重点实验室,长沙 410083;3.湖南中创空天新材料股份有限公司,湖南 岳阳 414000)
锂(Li)是世界上最轻的金属元素。将锂元素加入铝合金中,可在降低铝合金密度的同时,保持其较高的强度、耐热性以及延展性。铝锂合金相比于常规铝合金,其性能优良,具有极高的比强度和比模量[1];相比于复合材料,在抗冲击、塑性、修复性等方面优势不可替代。2195铝锂合金作为第三代铝锂合金,其超高的强度,优良的可锻性,可焊接性和低温性能[2],使其在Weldalite系列中应用范围最广,在航天航空领域具有很大的应用潜力[3]。
在近些年的研究中,各国学者针对不同合金体系,提出了不同的本构模型,常用的有宏观唯象学、微观物理基型以及基于人工神经网络本构模型[4-5]。各类模型都有着不同适用性和优缺点,其中,宏观唯象本构模型包括Johnson-Cook模型、Arrhenius模型等。已有研究表明,Arrhenius模型能较准确地预测金属热变形过程中变形温度、应变速率和真应力之间关系,应用较为广泛[6-7],所以2195铝锂合金流动应力、变形温度及应变速率之间的关系可以通过Arrhenius方程进行描述。采用热模拟实验方法研究不同金属材料的热变形行为、本构方程及热加工图的建立已有较多报道。张伟红等分析了NiTi合金热压缩实验结果,并对实验中因摩擦和温升效应引起的误差进行了修正,从而为NiTi合金高温塑性成型过程的数值模拟提供了精度较高的材料模型[8]。刘大博等采用修正后真应力真应变曲线建立了热加工图,优化出2D70铝合金合适的变形工艺范围[9]。然而,传统的热加工图仅考虑了变形的稳定性及可行性,并未评估变形的难易程度。近年来,有学者[10]将合金变形激活能与传统的热加工图相结合,提出了激活能加工(activating energy processing,AEP)图,可同时评估合金的变形稳定性及形变的难易程度,能更全面地反映合金的变形行为及热加工性能。
本工作采用热模拟实验方法,对2195铝锂合金在变形温度为400~490 ℃、应变速率为0.01~10 s-1条件下的热变形行为进行系统的研究,修正摩擦和温升效应带来的应力偏离,基于Arrhenius模型建立高预测精度的2195铝锂合金本构方程。基于修正的应力应变数据,将传统的热加工图与激活能进行耦合,建立材料的激活能加工图(AEP)。
1 实验材料
实验所用材料为美国铝业公司生产的2195铝锂合金,其实际化学成分如表1所示。
热轧后的2195铝锂合金进行双级均匀化热处理,工艺参数为440 ℃/16 h+490 ℃/20 h。然后,对热处理后的材料进行线切割,得到φ8 mm × 12 mm的试样并对表面进行磨光处理。利用Gleeble-1500D热模拟试验机将试样以5 ℃/s的加热速度分别加热到400 ℃、430 ℃、460 ℃、490 ℃,保温2 min后分别在应变速率为0.01 s-1、0.1 s-1、1 s-1、10 s-1下进行等温热压缩,变形量为60%,变形结束后迅速水淬冷却以保留变形后的组织,热压缩过程如图1所示。应变速率、温度、位移等变形条件是由电脑自动控制,并采集生成对应条件下的真应力-真应变曲线。

表 1 2195铝锂合金的成分(质量分数/%)Table 1 Chemical composition of 2195 aluminum alloy(mass fraction/%)
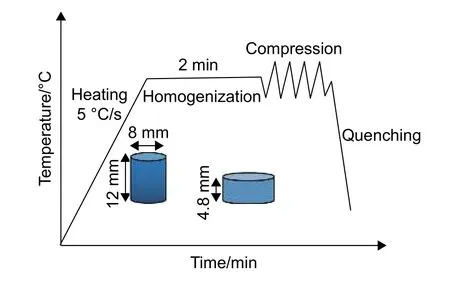
图 1 2195铝锂合金的热压缩过程Fig. 1 Hot compression test process of 2195 aluminum alloy
2 热压缩过程应力应变数据修正
在热压缩过程中,端面接触摩擦力的存在限制了金属的径向流动,导致压缩后的试样普遍存在鼓肚现象,改变了试样中的单向应力状态,使得压缩过程中试样的应力偏大,从而使所测真应力-真应变值与实际值产生较大的误差,因此需要进行修正。
根据实验测得的温度-时间曲线,绘制不同应变速率和温度条件下2195铝锂合金热压缩过程中温度变化的最大值分布,如图2所示。从图2可以看出,随着应变速率的增加,温升越来越明显,当应变速率为10 s-1时,不同温度下对应的温度变化的最大值相比其他应变速率下对应的最大值有明显的提升,试样实测温度普遍比预设温度高15 ℃以上。当应变速率小于1 s-1时,热变形过程中温度变化的最高值为4.82 ℃,在预设温度值中占比仅为1.2%,属于正常实验误差,因此只针对应变速率为10 s-1的真应力-真应变曲线进行温升效应的修正。
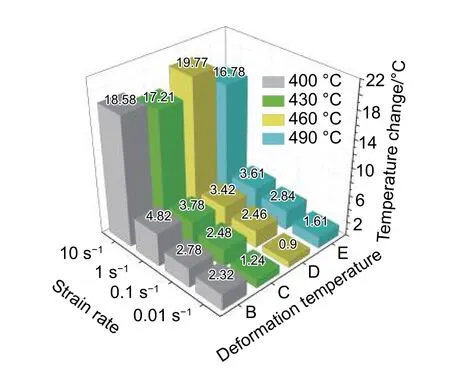
图 2 不同应变速率和温度条件下2195铝锂合金热压缩过程中温度变化的最大值Fig. 2 Maximum temperature changes of 2195 aluminum-lithium alloy during hot compression under different strain rates and temperatures
2.1 热压缩过程中摩擦力影响的修正
对2195铝锂合金压缩过程中因摩擦力存在而带来的应力偏离进行修正,修正后的真应力为:
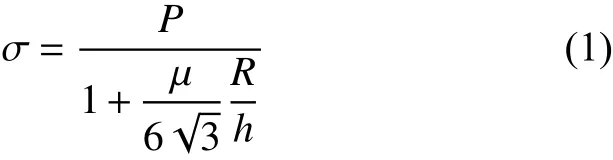
式中:P和σ分别为修正前后的真应力;R为试样的瞬时半径,由确定;R0为试样的初始半径;h0为试样的初始高度;h为试样的瞬时高度;μ为摩擦因子,其值可由式(2)和式(3)确定[11]:式中:
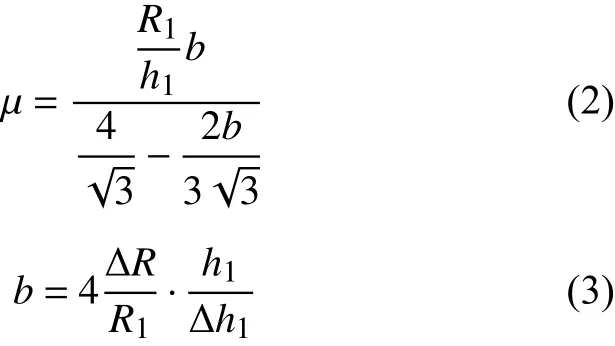
式中:R1为变形后试样的平均半径;h1为试样变形后的高度,Δh1=h0-h1;ΔR=RM-RT,RM为试样压缩后的最大半径,RT为压缩后压头与试样接触的底面半径,RT可由式(4)得到:
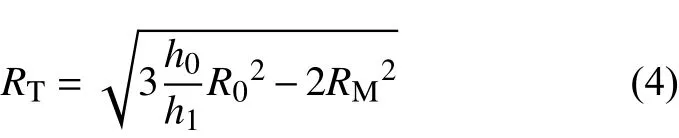
由式(1)~(4)可计算出修正后的流动应力。经过摩擦修正后的结果如图3所示。
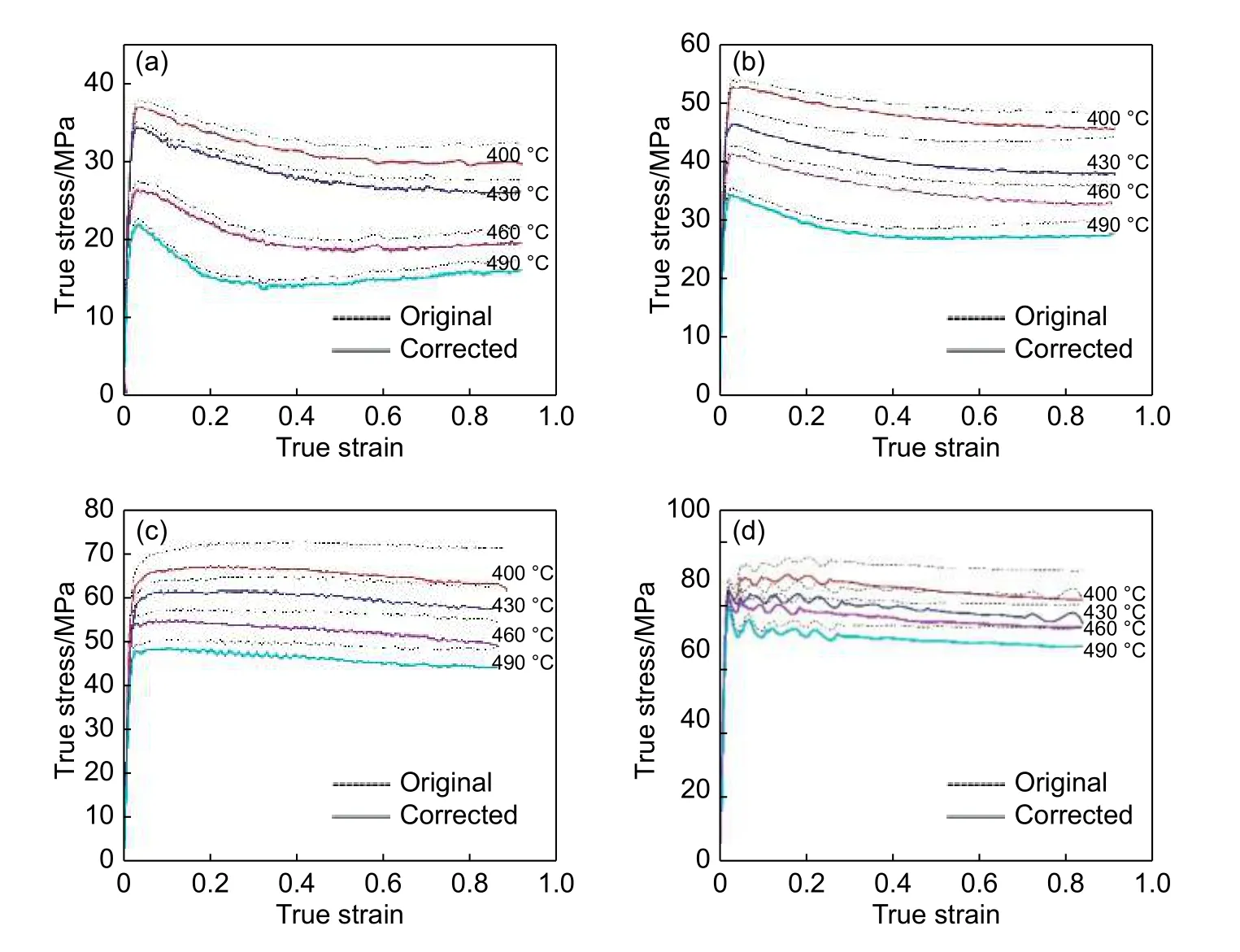
图 3 不同应变速率下2195铝锂合金摩擦修正前后的真应力-真应变曲线Fig. 3 True stress-true strain curves of 2195 Al-Li alloy before and after modification at different strain rates(a)0.01 s-1;(b)0.1 s-1;(c)1 s-1;(d)10 s-1
2.2 热压缩过程中温升效应的修正
温度的改变对流动应力的影响不可忽略,因此需在摩擦修正的基础上对应力进行温度修正。吴文祥等的研究结果表明,温度改变对流动应力产生的影响可表示为[12]:
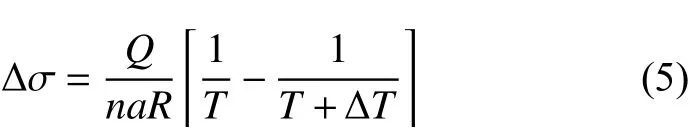
式中:Q为热变形激活能;R为摩尔气体常数,R=8.314 J·mol-1·K-1;T为绝对温度;n为应力指数;α为材料常数。
Baragar[13]研究表明,绝热温升效应带来的温度升高(ΔT)可由式(6)求出:

式中:c为比热容:ρ为密度;Δε为应变增量;β为产生热量所占总变形能量的比例,为85%~90%,其余能量则转变为其他形式(例如用于微观结构变化等)。应力增量值为:
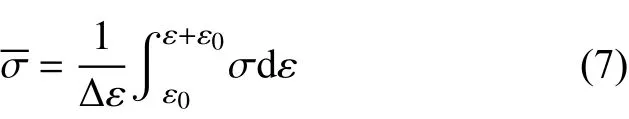
采用插值法[14]并结合式(5)~(7),对经过摩擦修正的应变速率为10 s-1的数据进行温度修正,修正后的结果如图4所示。
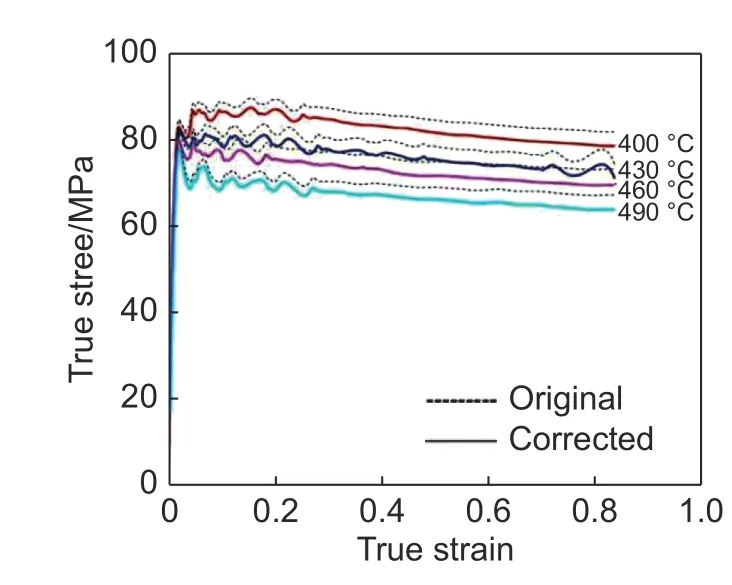
图 4 经摩擦修正又经温度修正后应变速率为10 s-1的真应力-真应变曲线Fig. 4 True stress-true strain curves with a strain rate of 10 s-1 after being corrected by friction and temperature
3 2195铝锂合金本构关系及热加工性能
3.1 流动应力
图3 和图4是2195铝锂合金在经过摩擦和温度修正后不同变形条件下的真应力-真应变曲线。由图3可知,在低应变速率下(0.1 s-1以下)其真应力在初始阶段随变形程度增加而迅速增大,达到峰值后逐渐下降。其原因是在变形初期,随着变形量的增加,位错密度急剧增加,加工硬化强于动态软化,从而导致应力值的快速增大,但随着变形程度的增加,位错产生了交滑移和攀移,使得动态软化强于或等于加工硬化,使得应力减小或保持稳定。在高应变速率下,例如在1 s-1时,应力上升到峰值,然后达到稳态值,表明合金在此条件下其应力达到动态平衡[15-17]。
另外,通过对比图3不同应变速率下的真应力-真应变曲线,在同样的应变速率下,流动应力随变形温度的增大而减小;在特定的变形温度下,流动应力和应变速率呈正相关,说明2195铝锂合金具有正的应变速率的特性。
3.2 2195铝锂合金的本构关系及预测模型
材料流动应力、变形温度及应变速率之间的关系可以通过Arrhenius方程来进行描述[18-19]
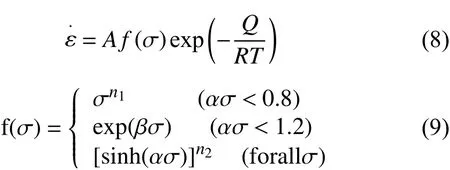
式中:T代表绝对温度,K;代表应变速率,s-1;R是气体常数,值为8.3145 J·mol-1·K-1;Q是塑形变形过程中的热变形激活能,J·mol-1;A、α、β、n1、n2代表材料常量,其中α=β/n1。
针对高温塑性变形条件的形变,其变形行为可以用包含Z-H参数表述,数学表达式如式(10)[20]:
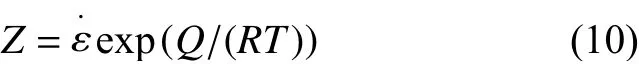
结合式(10)可得全应力水平的流动应力与变形参数之间的关系:
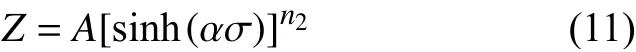
对式(11)进行求解,可以得到材料的本构方程为:
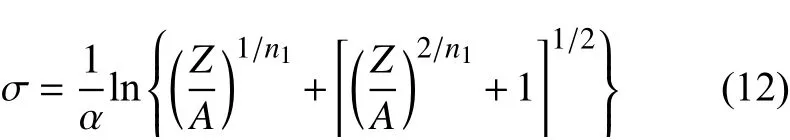
由式(8)和(9)可推导出:

由式(13)~(15)可知,n1和β分别是ln-lnσ和 ln-σ曲线的斜率;n2是lnε·-ln[sinh(ασ)]的斜率,利用origin软件进行线性回归并绘制出应变速率和流动应力关系曲线图,如图5所示。在计算n1时,对于图5(a),选取峰值应力小的数据点,计算其斜率的平均值n1= 5.89817;对于图5(b),取峰值应力大的数据点,得其斜率的平均值β=0.135075,由β和n1值可得α=β/n1= 0.0229。对于图5(c),取所有曲线的斜率求其平均值易得最终应力指数值n2= 4.696。

图5 应变速率与流动应力关系曲线Fig. 5 Relationship curves of strain rate and flow stress(a)l n -lnσ ;(b)l n -σ;(c)l n -ln[sinh(ασ)]; (d)ln[sinh(ασ)]-1/T图 5 应变速率与流动应力关系曲线Fig. 5 Relationship curves of strain rate and flow stress (a)l n -lnσ ;(b)l n -σ; (c)l n -ln[sinh(ασ)]; (d)ln[sinh(ασ)]-1/T

图5 应变速率与流动应力关系曲线Fig. 5 Relationship curves of strain rate and flow stress(a)l n -lnσ ;(b)l n -σ;(c)l n -ln[sinh(ασ)]; (d)ln[sinh(ασ)]-1/T图 5 应变速率与流动应力关系曲线Fig. 5 Relationship curves of strain rate and flow stress (a)l n -lnσ ;(b)l n -σ; (c)l n -ln[sinh(ασ)]; (d)ln[sinh(ασ)]-1/T
对于所有应力状态,先假定变形激活能Q与温度T无关,Q可以由式(16)得:
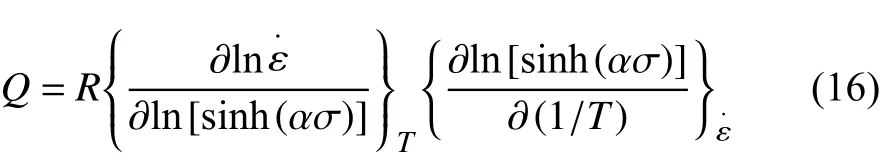
此外,不同应变速率和变形温度的效果可以由Hollomon和Zener提出的Z参数来表述,其表达式如式(17)所示:
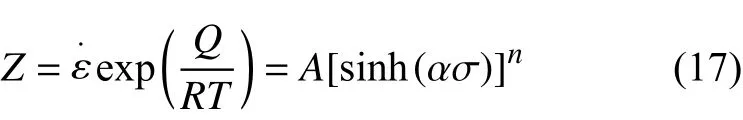
对式(17)两边求自然对数可得:
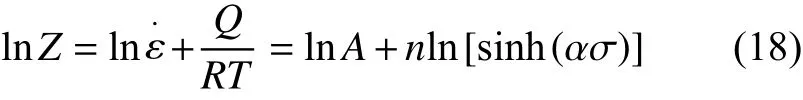
图6 为lnZ-ln[sinhασ]的关系图。通过图6可以得到式中 l nZ-ln[sinh(ασ)]直线关系的截距lnA=15.676,直线斜率n= 4.62845,因此A= 6.427 × 106。
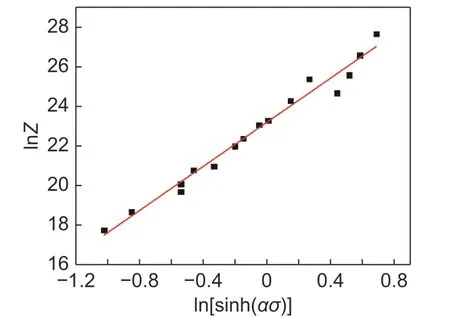
图 6 lnZ-ln[sinhασ]的关系Fig. 6 Relationship curve of lnZ-ln[sinhασ]
综上可得2195铝锂合金高温流动应力本构方程如下:
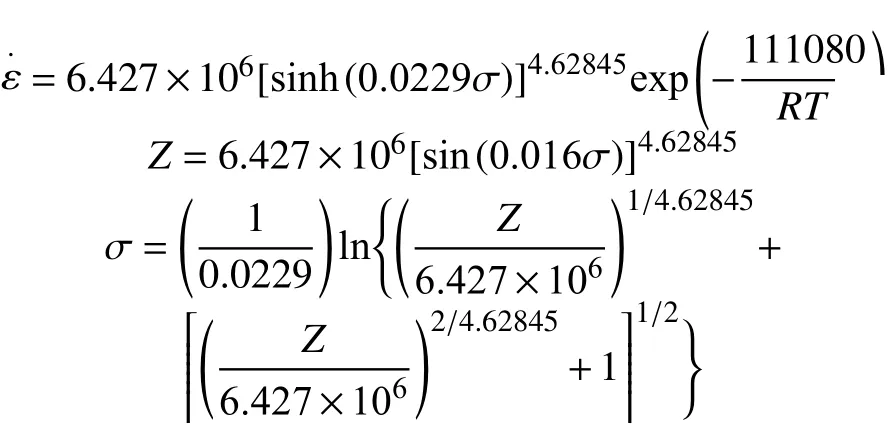
3.3 建立应变补偿模型
基于修正后的实验数据,仿照上述求解本构方程的方法,在应变范围0.1~0.8内每隔0.1选取一个值,求得不同应变下的材料参数(lnA、Q、α、n),如表2所示。

表 2 2195铝锂合金在不同应变下的ln A、Q、α、n的值Table 2 ln A,Q,α,n values of 2195 aluminum-lithium alloy under different strains
然后对2195铝锂合金的各个参数进行5次多项式的拟合,在多项式拟合后,各个参数与应变量之间的函数式如式(19)~(22):

拟合曲线如图7所示。为了检验应变补偿本构模型的预测精度,首先,取修正后的流动应力实验值和预测应力值进行比较,其最终结果如图8所示。由图8可以看出,在变形过程中,模型的预测值和实验数据拟合较好,为了更为直观地评估模型的拟合程度,引入了标准统计参数即相关系数(R)和平均绝对误差(AARE)来对预测精度进行进一步的评估:
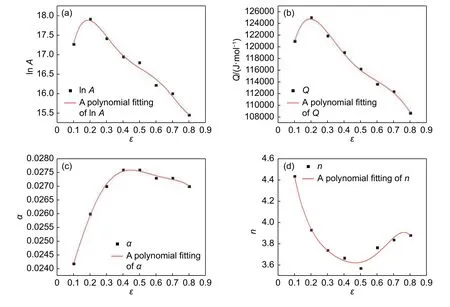
图 7 应变ε与各参数的关系曲线(a)ln A;(b)Q;(c)α;(d)nFig. 7 Relationship curves between strain ε and parameters(a)ln A;(b)Q;(c)α;(d)n
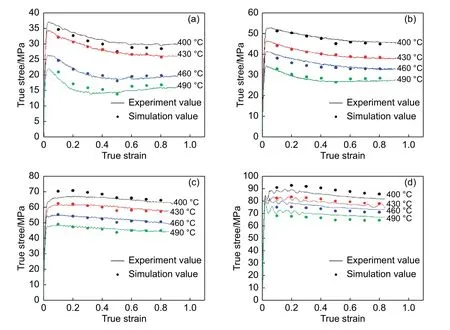
图 8 不同应变速率下修正后的流动应力实验值与预测值对比Fig. 8 Comparison of modified flow stress test value and predicted value at different strain rates(a)0.01 s-1;(b)0.1 s-1;(c)1 s-1;(d)10 s-1
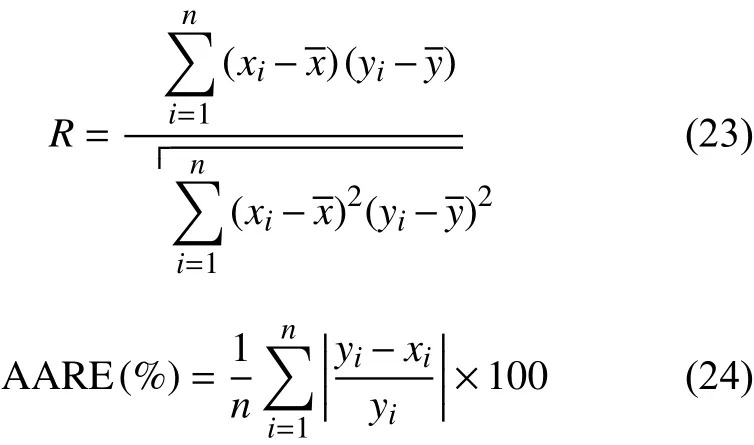
式中:yi为实验测得的真应力值;xi为考虑应变补偿后计算所得的预测值;n是研究的流动应力数据点的个数。
图9 是所有应变条件下的实验数值与预测数值的对比图,结果表明:实验值和预测值的相关系数R为0.99584,平均绝对误差(AARE)仅为3.698%,充分说明该本构模型能够准确预测2195铝锂合金在不同变形参数下的流动应力值。
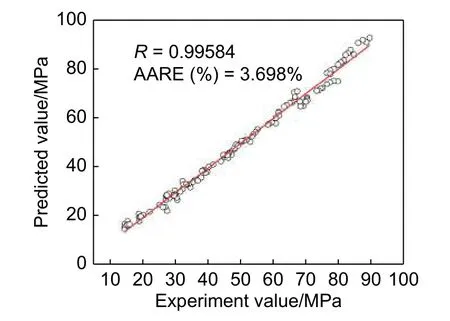
图 9 实验数值与预测数值对比Fig. 9 Comparison of experimental and predicted values
3.4 热加工性能
热加工图可评价材料加工性能优劣进而优化材料的加工工艺参数。根据加工图,可以获得该材料的失稳区域和热加工区域[2],加工过程中单位体积内材料所吸收的能量P可以分为耗散量(G)和耗散协量(J)两个互补函数:

材料的强度随塑性应变率的增加而增加,可得[21]:

变形过程中的应变速率敏感指数m和功率耗散效率η可分别表示为[21]:
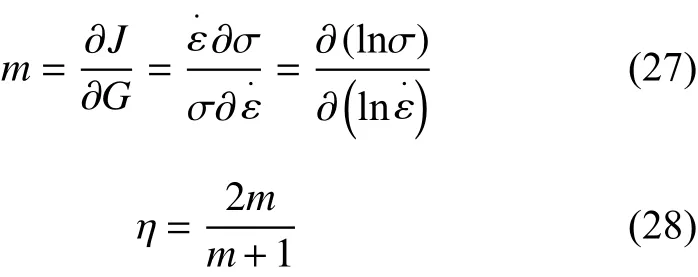
式中:η代表材料塑性变形过程中微观组织结构演化所耗散的能量与线性耗散能量的比值。
η的增加意味着微观组织演化所消耗功率的增加,以耗散系数为函数,可以通过温度和应变速率绘制出能够显示在不同区域内不同组织变化机制的耗散图。其中适合加工的区域通常具有较高的耗散系数η,但功率耗散系数η越高并不能代表材料的加工性能就越好,因为材料还存在有加工失稳区,材料在此区间内变形会产生失稳的现象。据此Prasad等[21]根据Ziegler提出的最大熵产生率原理,建立了基于不可逆热力学极值原理的连续不稳定判据:
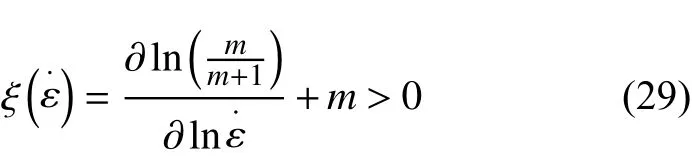
当稳定判据小于0时,则系统进入流变失稳区,以流变失稳准则为函数,将功率耗散图和流变失稳图以等高线的形式进行叠加,就可以得到流变失稳图(CHP)。虽然常规流变失稳图(CHP)考虑了变形的稳定性,但没有考虑变形的困难,即是否容易发生变形。因此,CHP映射难以高效、准确地获得最优的加工参数。基于式(16),本工作计算出不同应变条件下的激活能值Q,通过将CHP映射与激活能值耦合,建立了激活能加工(AEP)图[22-23]。
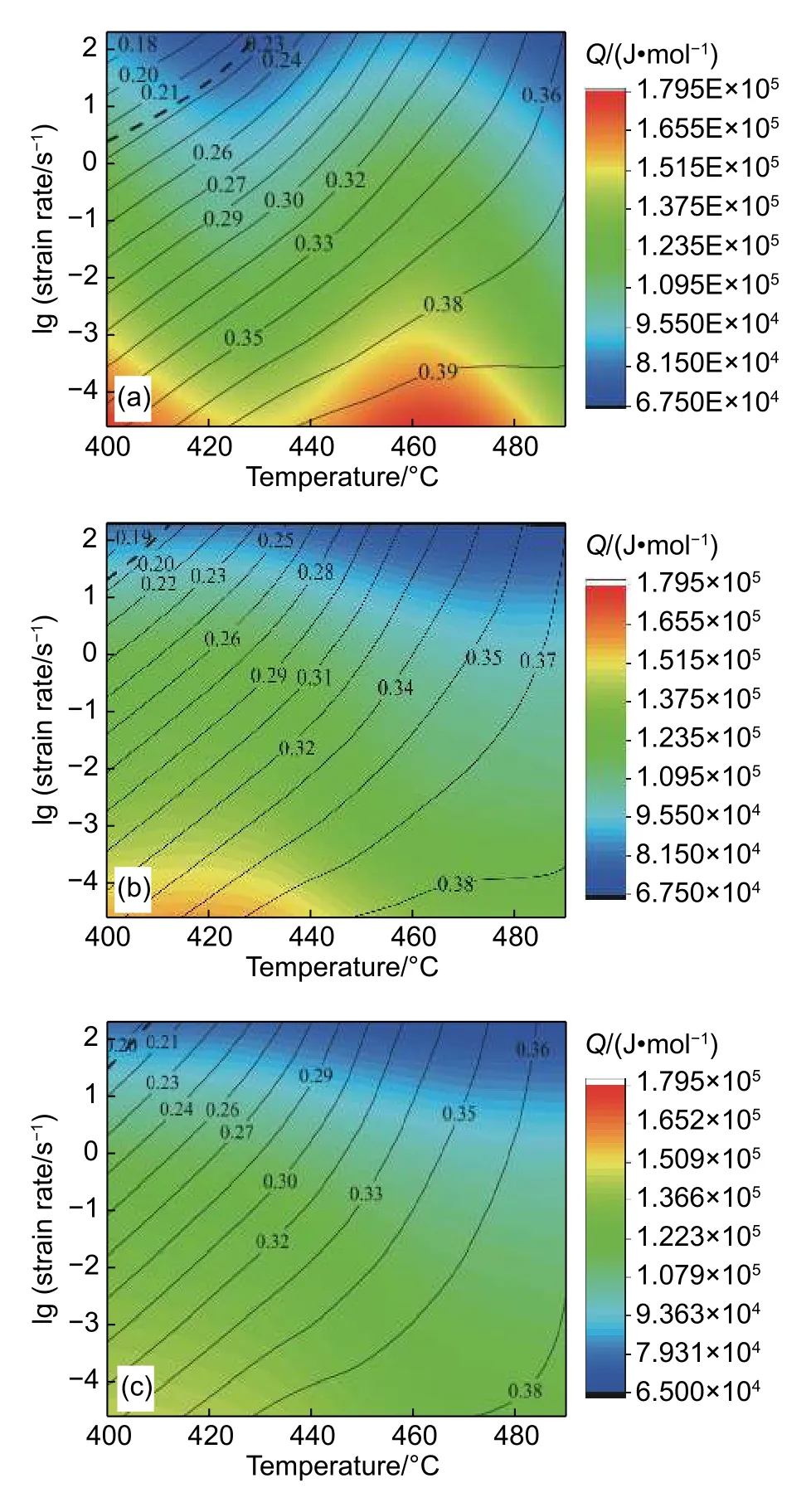
图 10 不同应变下的AEP图Fig. 10 AEP diagrams under different strains (a)0.4;(b)0.6;(c)0.8
图10 为2195铝锂合金在不同应变条件下的AEP图。图10中等高线上的数据表示功率耗散效率η,不同颜色对应不同的激活能Q,具体的数值见右边的颜色标尺栏,其大致可分为红绿蓝三个区域,红色区域的激活能较高,属于难变形区域;蓝色区域的激活能比较低,属于易变形区域;绿色的区域激活能为前两者之间,属于稳定流变区域。对于金属材料来讲,较高的Q值(红色区域的激活能)表示合金在该区间发生变形时需要消耗更多能量,不利于材料加工,所以选择加工区间时候应该尽量避免,如变形温度为400~430 ℃,应变速率为0.05 s-1以下和变形温度为430~485 ℃,应变速率为0.1 s-1以下的区域。而最适合加工(蓝色)的区域主要集中 在400~450 ℃/ 1~10 s-1以 及450~490 ℃/3~10 s-1范围内。但从图10可以看出,400~450 ℃/1~10 s-1是黑色虚线包围的区域,是流动不稳定的区域(即η≤ 0),所以不能作为合金的适合加工的区域。考虑到适宜加工的区间还应该具有η值高和轮廓线稀疏这两个特征,综合考虑各个应变下的AEP图,适宜选择的加工工艺为应变速率0.4 s-1以下、温度为475~490 ℃的区域。
4 结论
(1)对2195铝锂合金圆柱体试样进行了变形温度为400~490 ℃、应变速率为0.01~10 s-1条件下的等温热压缩实验,并对实验获得的真应力应变曲线进行摩擦力和温升效应的修正。修正后2195铝锂合金的变形激活能Q= 111080 J/mol,流变本构方程为:
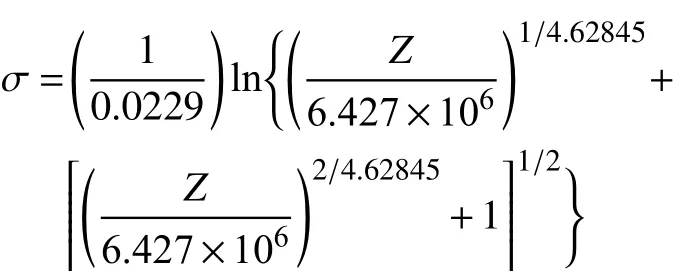
(2)通过验证和计算,Arrhenius模型的相关系数R= 0.99584,平均绝对误差(AARE)=3.698%。修正后的本构关系,可很好地预测2195铝锂合金的变形应力。
(3)综合考虑各个应变下的激活能加工(AEP)图,2195铝锂合金适宜选择的加工工艺为应变速率0.4 s-1以下、温度为475~490 ℃的区域。

