面向倾斜摄影测量数据的out-of-core调度机制

曾红梅，刘子桓

（四川大学计算机学院，成都610065）

0 引言

随着城市信息化应用水平不断提升，智慧城市建设应运而生[1]。以OpenSceneGraph（OSG）三维渲染引擎为代表的场景可视化系统，为实时显示大规模城市场景提供了巨大支持[2]。然而，近几年CPU和GPU发展迅速，内存和硬盘的发展较为缓慢，数据访问速度成为大规模场景可视化的主要瓶颈[3]。并且，大规模场景的LOD模型数据量通常十分庞大[4]，不能常驻内存和显存，可视化系统需要利用out-of-core技术完成场景LOD模型内外存调度工作。因此，研究大规模场景LOD模型out-of-core调度机制，对推动智慧城市建设具有重要意义。

目前，主要通过基于几何的建模和基于图像的建模两种方式获取场景模型[5]。随着无人机的飞速发展，通常利用无人机倾斜摄影的方法，高效地采集到真实度高的场景数据，然后通过几何校正、影像匹配和空中三角测量技术处理测量得到的数据，最终基于图像建模大规模场景[6]。其中倾斜摄影测量技术[7]是近年的一种新兴测量技术，从垂直、倾斜等不同角度采集影像，以获得地面物体更为完整准确的信息[8]。

同时对于大规模场景内外存调度问题，主要通过改变场景数据内外存组织形式和改进场景数据调度机制两种方式解决。Da Silva等[9]将大型点云数据组织成动态八叉树结构，设计了一种基于部分排序的Morton码，提高外存数据查询效率。Gong等[10]结合八叉树和R树叶子节点，提出3DORTree概念和一种基于深度遍历与广度遍历的混合遍历方法，对场景数据组成的3DORTree进行遍历。Lindstorm等[11]解决地形可视化问题时，让操作系统控制内外存数据分页工作，提出使用内存映射技术加快内外存数据调度效率。高宇等[12]利用最近最少使用策略（least recently used，LRU）释放内存，对可能用到的内存数据进行加锁处理，减少内外存数据访问次数。Xue等[13]提出一种高效的可交互CAD模型的GPU内外存调度渲染框架，将LOD模型压缩成高度紧凑的格式，最小化存储成本。Jia等[14]针对大规模地址学模型场景可视化系统，在外存中根据模型的特点构造多分辨率简化模型。Deibe等[15]开发了VILMA可视化软件用于大规模LiDAR点云数据渲染，并且提出Hierarchically Layered Tiles和Tile Grid Partitioning Tree两种数据组织方式减少内外存占用率。OSG三维渲染引擎通过DatabasePager实现场景LOD模型动态out-of-core调度机制[16]。

OSG调度机制采用逐层次方式加载LOD模型，LOD节点树在加载过程中才被建立，导致OSG无法跨层次加载LOD节点。即使预先保存LOD节点树，然后载入使用，OSG却不知道是否在一帧内能完成目标LOD节点的加载。从而，OSG为了保证系统帧率，采用了最保守的逐层次加载方法。

但是，OSG逐层次加载的方式导致如下两个问题：①加载数据量大。因为在加载到目标LOD节点之前，需要加载所有中间层次节点。②未考虑外存设备读取能力。即使外存设备读取能力强，OSG仍然在每帧中，将加载和渲染的LOD层次，向精细化方向只推进一层。从而导致限制时间内，OSG无法加载到用户期望的LOD层次，最终渲染效果达不到用户的期望。

针对上述OSG调度机制的缺陷，本文提出跨越式的LOD模型out-of-core调度机制。为了使系统可以跨层次加载LOD节点，本文预计算生成场景LOD节点树保存在外存。并且，在限制时间内不能完全加载用户期望的LOD节点时，为了找到替代效果最佳的LOD节点集合，本文利用多选择背包问题[17]方法，求解得到最优的节点集合。对比OSG，本文大量减少LOD节点数据量和数据总加载量，并且提升场景渲染效果。

1 算法实现

当不能完全加载用户期望的节点时，为了找到替代效果最优的节点集合，本文利用多选择背包问题（multiple-choice knapsack problem，MCKP）[17]方法求取最优解。由于每组物品数量巨大，导致求解多选择背包问题时间复杂度极高。因此，本文提出物品模板的概念，通过物品模板实时生成少量物品，降低求解时间复杂度。

1.1 求解最优节点集合

将如何找到替代效果最优的节点集合的问题抽象为多选择背包问题，再利用动态规划算法求解多选择背包问题[18]。

首先明确合法调度节点集合和期望节点集合的概念，当合法调度节点集合L包含某个节点Nnode时，则此节点的所有兄弟节点Nbrother∈L，所有子孙节点Nchild∉L。将场景被化分为n个块（Tile），根据当前视点信息进行可见性计算和LOD计算后，由各个Tile中符合计算结果的LOD节点组合成的集合Hi，所组成的集合H={H1,H2,H3,…,Hn}成为期望节点集合。

已知外存设备读取速度，在限制加载时间内，将每帧节点调度中允许的LOD节点最大加载量Wtotal视为背包重量。将每个Tile视为一组物品集合，假设第i个Tile的LOD节点树有mi个LOD节点，有ki种合法调度节点集合，将每种合法调度节点集合视为一个物品，物品重量Wki为集合中所有节点加载量之和，物品收益Vki为结合种所有节点三角形面片数量之和。在每帧LOD节点调度中，当期望节点集合加载量WH>Wtotal，导致无法完全加载期望节点集合时。如公式（1），从每个可见Tile的ki种合法调度节点集合Li中选择一种即从每组中选择一个物品，使得加载所有已选择物品产生的总收益Vactual最大。如公式（2）保证所有被选择物品的总加载量Wactual≤Wtotal。如公式（3）表示最多只从每个可见Tile中选择一种合法调度节点集合即物品，如公式（4）表示物品是否被选择。

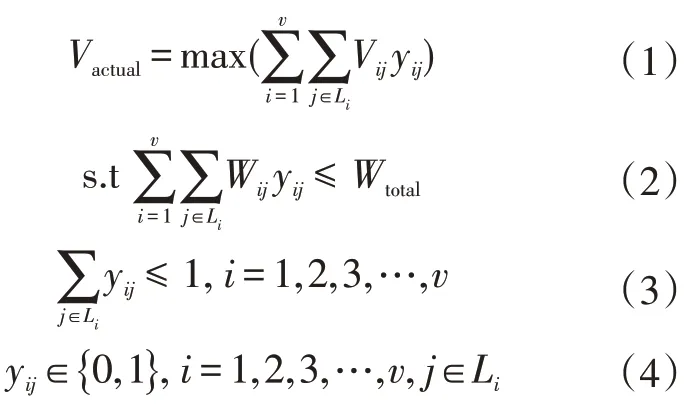
其中v表示当前可见Tile数量。Vij表示第i个可见Tile的第j种合法调度节点集合收益，同理Wij表示其加载量。yij=0表示这种合法调度节点集合不被选择，yij=1表示被选择。

如图1，使用一个例子说明本文利用多选择背包问题求解的思想。假设场景中经过可见性计算后，只有Tile1和Tile2，并且期望节点集合分别为A={6 ,7,8,5}，B={6,7,4}。在一帧节点调度中，最大加载量Wtotal=15，期望节点集合加载量WH=32。因此，需要从每个可见Tile的所有合法调度节点集合中最多选择一种加载，使得节点加载总量Wactual≤Wtotal的前提下，加载总收益Vactual最大。Tile1和Tile2分别有6种、4种合法调度节点集合，在24种组合中，Tile1选择C={6,7,4,5}，Tile2选择D={1}加载后产生最大收益为15。最终，此次节点调度应该选择集合C和D进行加载显示。

图1加载LOD节点过程

但是，多选择背包问题被证明是NPC问题[19]，求解时间复杂度与每组物品数量呈指数级相关。根据公式（5）计算根节点的组合代表一个Tile中的合法调度节点集合数量即物品数量。如表1所示，在四川大学场景中，计算得到部分Tile的合法调度节点集合数量。每个Tile的合法调度节点集合数量巨大，导致求解十分困难，无法保证系统的实时性。

其中c表示节点的子节点数量，kj表示子节点的组合数，k表示节点的组合数。叶子节点没有子节点，则kleaf=1。

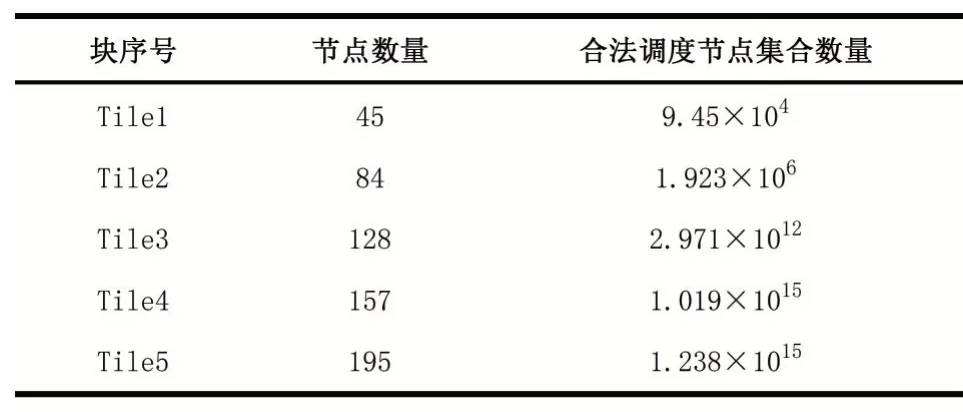
表1合法调度节点集合数量

因此，本文提出通过物品模板实时生成少量物品，降低时间复杂度。

1.2 生成物品模板集合

本文提出物品模板的概念。首先，通过离线处理方式，预计算生成少量合法调度节点集合作为物品模板集合。然后，在系统运行时，根据可见性计算与LOD计算生成期望节点集合，结合保存节点加载量、三角面数量和节点文件是否在内存等信息的节点状态表，实时地从各个物品模板中生成物品。最后，每个Tile中的物品数量大量减少，使得求解节点调度最优化问题容易。本文提出BaseN节点集合作为物品模板，其定义如下：

定义BaseN节点集合：每个Tile的LOD节点树中，以深度为N的全部节点以及深度小于N的所有叶子节点组成的集合，称之为BaseN节点集合。

本文使用如图2的一个例子说明BaseN节点集合。其中，基于深度4的Base4集合，由深度为4的节点{10,11,12,13,14,15,16}和小于深度的全部叶子节点{5,8}组合而成。

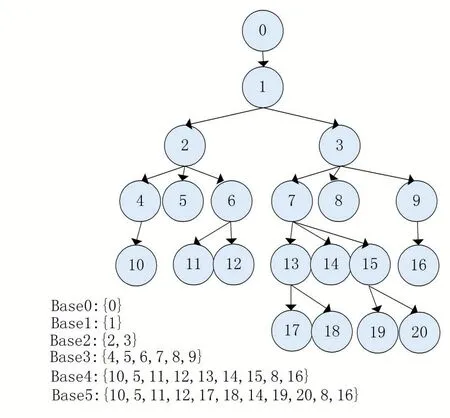
图2 Tile中BaseN节点集合

本文将BaseN节点集合为物品模板的理由如下：

（1）是合法调度节点集合。当物品模板自身不是合法调度节点集合时，必须花费时间令其转变为合法的。

（2）覆盖LOD节点树的各个层级。当物品模板未覆盖到某些层级时，将会影响最终节点调度最优化问题的求解。

（3）能快速生成物品。当面临不符合LOD计算以及剔除计算结果的节点，可以快速将节点从BaseN节点集合中删除或者替换，然后生成物品。

最后，预计算为场景中每个Tile生成BaseN节点集合保存在外存，当系统运行时，实时根据可见性计算和LOD计算生成物品。

1.3 生成物品

本文为场景中所有Tile生成BaseN节点集合时，默认所有Tile的所有节点可见。但是在系统运行时，用户的视点位置变换，将会出现部分Tile不可见和部分节点不可见的情况。因此，在每次节点调度时，需要根据视点信息，将物品模板转化为真正的物品，才能作为多选择背包问题的输入。本文算法结合期望节点集合以及节点状态表，从物品模板中生成物品，具体生成步骤如下：

（1）复制所有BaseN节点集合作为待处理的物品模板集合。

（2）进行可见性计算，删除不可见Tile的物品模板集合，以及可见Tile物品模板中的不可见节点。

（3）根据期望节点集合，得到每个Tile对应期望节点集合中的最大节点深度Ni。删除Tile中最大节点深度大于Ni的物品模板。

（4）将物品模板中，不符合LOD计算结果的节点，替换为符合LOD计算的祖先节点。并且根据节点状态表，标记物品模板中已经存在于内存中的节点，表示该节点的加载量为0。最终每个物品模板中，剩余的节点组合成物品，即每个Tile中实际可选择的合法调度节点集合。

最后，将生成的物品作为多选择背包问题的输入，求解得到替代效果最佳的节点集合，作为系统此次调度的实际节点集合。即每个可见Tile中仅有少量的物品，从每个Tile中最多选择一个物品，组成的物品集合加载量不超过限制加载量，并且使得系统渲染效果最好。

2 实验结果

2.1 实验环境

本文实验环境如表2所示。

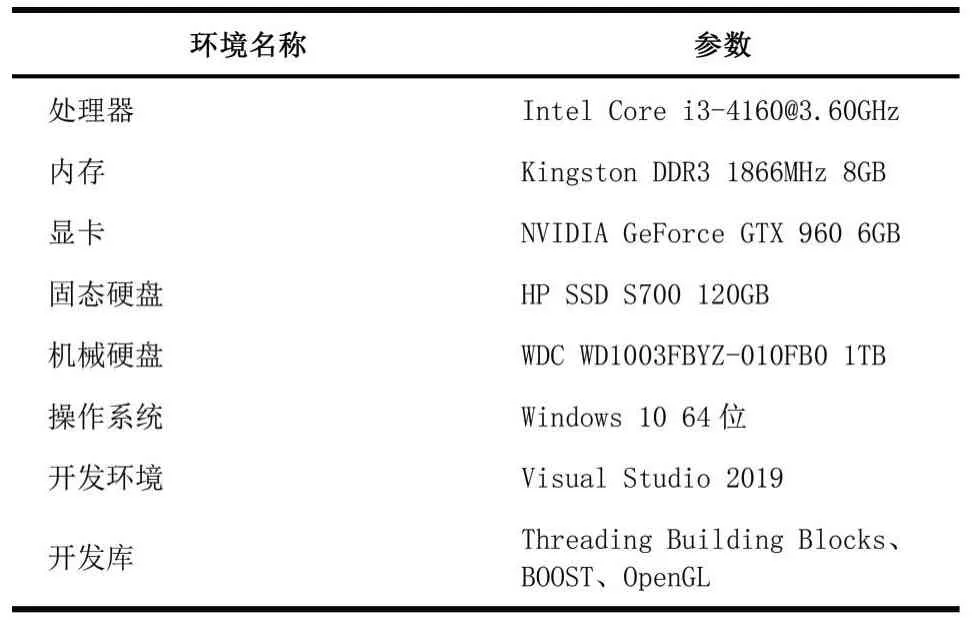
表2实验环境

通过精灵Phantom 4 RTK型无人机在成都市青羊宫和四川大学周边进行倾斜摄影采集到的两套数据，详细信息如表3所示。

表3无人机采集数据

使用Bentley System公司的ContextCapture软件[20]对采集到的数据处理，自动建模三维场景。然后，仅保留模型文件OpenSceneGraph Binary（OSGB）中关于LOD节点调度的相关信息。最终，生成本文用于场景LOD模型调度机制研究的数据格式，包含bin、bint、lodtree这3种格式文件。二进制几何数据文件（.bin）保存LOD节点的几何数据，二进制纹理数据文件（.bint）保存LOD节点的纹理数据，LOD节点树文件（.lodtree）保存多个LOD节点的信息以及节点间的关系。调度文件相关信息如表4所示。

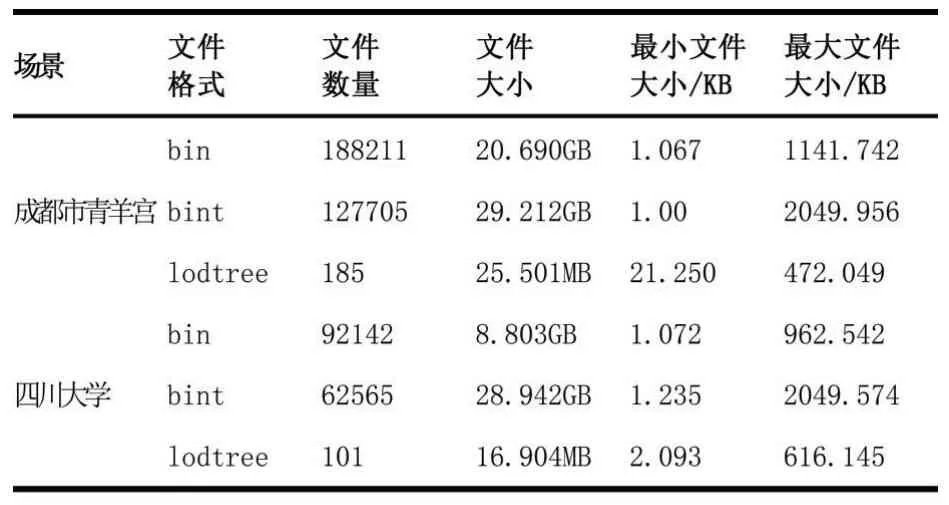
表4调度文件相关信息

2.2 数据加载量对比实验

本实验对比本文算法和OSG逐层次调度机制的LOD节点数量与数据总加载量，证明本文算法在每次调度时，能够大量减少需要加载的LOD节点数量和数据总加载量。

实验中记录了在同一场景的同一视点位置处，调度相同的期望LOD节点集合时，OSG逐层次调度机制和本文算法加载的LOD节点数量与节点数据总加载量。分别在成都市青羊宫和四川大学场景下进行实验，实验结果如表5和表6所示。

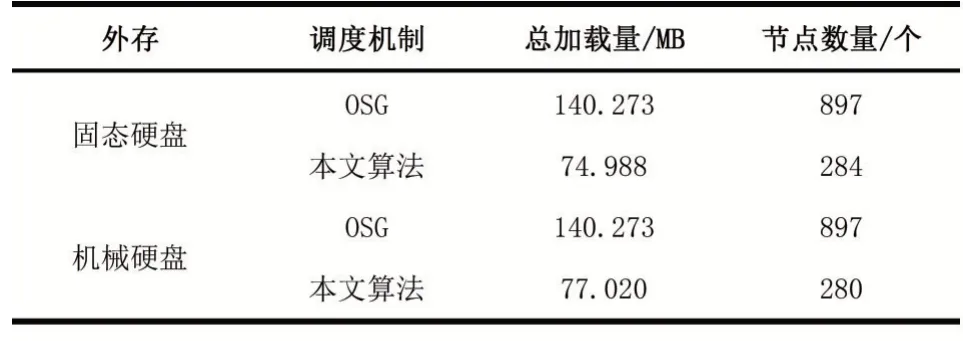
表5成都市青羊宫场景加载信息记录

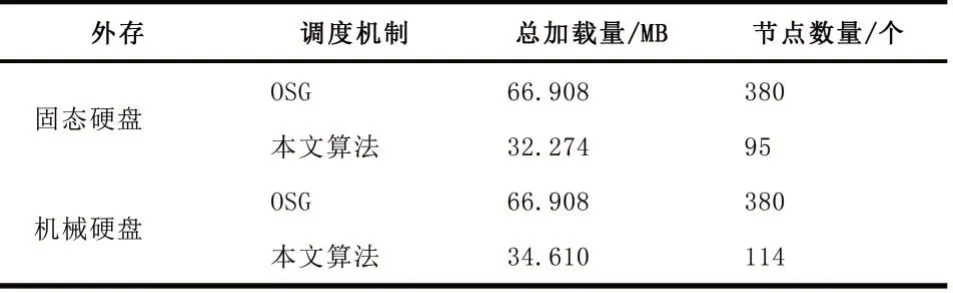
表6四川大学场景加载信息记录

由表5和表6实验结果可以看出，在相同场景和外存设备的条件下，本文算法的数据总加载量为OSG的50%左右，加载的LOD节点数量为OSG的30%左右。例如在成都市青羊宫场景，固态硬盘的条件下，OSG需要加载897个节点才能显示用户期望的效果，数据总加载量为140.273 MB，然而，本文算法只需要加载284个LOD节点，数据总加载量为仅为74.988 MB。

同时，OSG对于具有不同读取能力的外存设备，调度的总节点数量不变。但是本文算法在不同的外存读取能力下，调度的总节点数量不同。例如四川大学场景中，OSG在固态硬盘和机械硬盘上调度的节点数量都是380个，本文算法在固态硬盘上调度的节点数量为95个，在机械硬盘上调度的节点数量为114个，因为本文是在外存设备读取范围能力内，求解多选择背包问题得到的替代节点集合，所以不同的外存设备下，求解结果不同，最终总共需要加载的LOD节点数量也不同。

OSG为了保证系统帧率，将数据加载压力分摊到了多个渲染循环中，逐层次的加载节点。从而必须加载所有中间层次节点，导致加载的LOD节点数量更多。相比之下，本文算法不需要加载中间层次节点，当加载能力足够时，则直接加载期望的LOD节点，当加载能力不足时，在限制时间内，求解多选择背包问题，完成节点加载工作。

2.3 渲染效果对比实验

本实验在四川大学场景的同一视点位置下，对比本文算法与OSG逐层次调度机制加载显示LOD节点的渲染效果。

本文算法使用加载的LOD节点集合拥有的三角形面片数量衡量渲染效果，在不同的限制时间条件下进行实验，实验结果如表7所示。

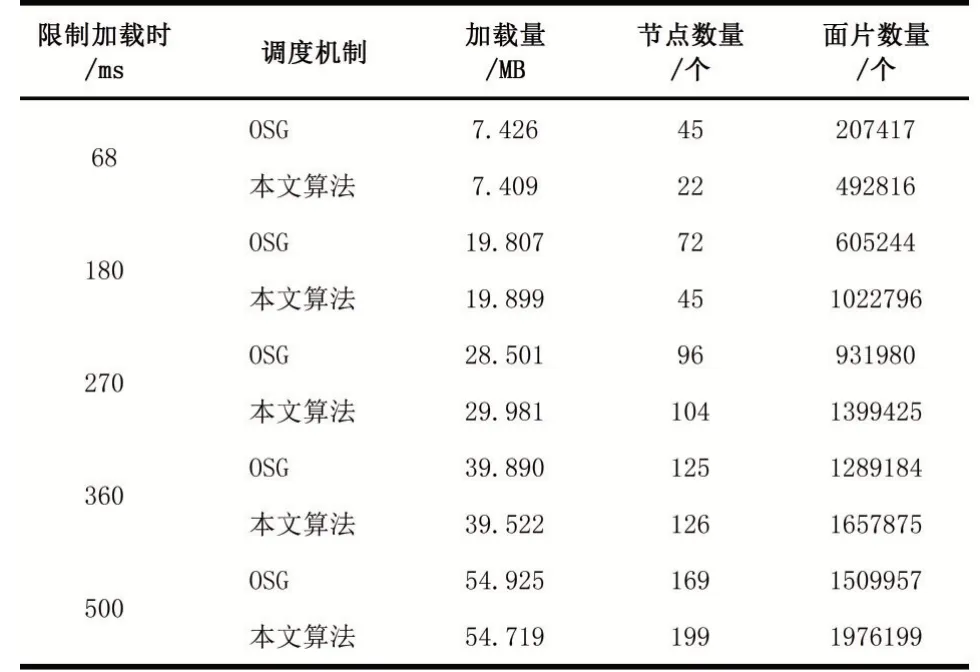
表7节点加载效果表

由表7可知，在不同限制时间条件下，本文算法最终渲染的LOD节点集合拥有的三角形面片数量是OSG的140%左右。在限制加载时间为500 ms时，图3为OSG的渲染效果，图4为本文算法渲染效果，图5为用户期望的节点渲染效果。对比图3和图4可以从看出本文算法的渲染效果比OSG更加清晰。分别对比图3与图5、图4与图5，可以看出本文算法效果更加接近用户期望显示的效果。

图3 OSG渲染效果

图4本文算法渲染效果

图5期望渲染效果

实验结果表明，OSG渲染效果不如本文算法。分别求取本文渲染效果图4与期望渲染效果图5和OSG渲染效果图4与期望渲染效果图5的结构相似性SSIM、峰值信噪比PSNR和均方误差MSE，结果如表8所示，可知本文方法的渲染效果更好，结构相似度更高，均方误差更小，峰值信噪比更高。由于不能完全加载到用户期望的LOD节点，OSG最终加载显示某个中间层次的LOD节点集合。而本文算法求解多选择背包问题，最终加载显示的渲染效果最优的中间层次LOD节点集合。

表8渲染效果比较

3 结语

本文使用多选择背包问题求解出替代效果最优的LOD节点集合进行加载显示，并且提出物品模板与物品的概念降低求解时间复杂度，最终实现了面向倾斜摄影测量数据的跨越式LOD模型out-of-core调度机制。实验结果表明，对比OSG，本文算法在每帧调度中，大量减少了需要加载的节点数据总加载量和节点数量，并且渲染效果比OSG更精细。本文算法对于大规模城市场景的可视化具有一定的价值和参考。不足的是本文假设读取不同数量、不同大小的文件耗时相同，视外存设备读取速度为常数，导致对调度最优化问题的求解有一定影响，后续考虑利用回归森林方法预测出外存设备的读取速度。并且，本文求解调度最优化问题时，为了降低求解时间复杂度，进而求取次优解作为最终结果。因此，找到降低时间复杂度的，且渲染效果比本文算法更好的方法是本文未来继续的研究方向。