基于梯度下降法直接拟合光谱吸收信号的气体浓度测量方法研究
邵国栋, 李峥辉, 郭松杰, 邹丽昌, 邓 瑶, 卢志民, 2, 3, 姚顺春, 2, 3*
1. 华南理工大学电力学院, 广东 广州 510640 2. 广东省能源高效清洁利用重点实验室, 广东 广州 510640 3. 广东省能源高效低污染转化与工程技术研究中心, 广东 广州 510640
引 言
可调谐二极管激光吸收光谱(tunable diode laser absorption spectroscopy, TDLAS)技术由于选择性强、 灵敏度高、 精确度高、 非侵入式测量等优点, 被广泛应用于大气环境监测、 燃烧流场诊断、 工业过程控制、 人体呼吸探测等领域[1]。 可调谐二极管激光器有两种最广泛使用的吸收光谱技术: 直接吸收光谱技术和波长调制光谱技术。

已有的基线拟合研究主要集中在对基线进行修正和对误差进行校准两个方面。 在此基础上, 提出了一种新的浓度反演方法: 基于梯度下降法直接拟合光谱吸收信号, 即直接拟合法, 对透射激光强度进行拟合以提取光谱和浓度信息, 并通过测量不同浓度的CO2, 验证该方法的可行性和准确性。
1 理论分析
1.1 Beer-Lambert定律
根据Beer-Lambert定律, 一束激光穿过气体, 其透射信号与入射信号的关系可表示为[7]
It=I0e-PSLxφ(ν)
(1)
式中,It为透射激光强度,I0为入射激光强度;P[atm]为被测气体的总压强;S[cm-2·atm-1]为吸收谱线的线强, 可以通过分子光谱数据库HITRAN确定[9];L[cm]为光程长度;x是目标气体的浓度, 用体积分数表示;φ(ν)为线型函数, 表示被测气体吸收谱线的形状, 本文以洛伦兹线型拟合吸收谱线。

(2)
(3)
式中,A是积分吸光度, 通常用式(3)计算目标气体浓度, 即积分面积法, 也称为吸光度曲线拟合法。
1.2 梯度下降法的基本原理
梯度下降法是一种经典的数值优化算法, 用来递归性地逼近最小偏差, 常作为机器学习领域训练算法的核心内容被应用于人工神经网络与逻辑斯谛回归。 它的主要思想是: 首先对系数向量初始化, 然后逐步迭代更新系数向量值, 进行目标函数的极小化, 直到收敛。 由于负梯度方向是使函数值下降最快的方向, 所以在迭代的每一步以负梯度方向更新系数向量值, 从而达到减少函数值的目的[9]。
假设函数f(x)在xk附近连续可微, 且gk=▽f(xk)≠0, 对于求解f(x)极小值问题, 梯度下降法计算步骤如下[10]:
步骤1 给出x0∈R, 0≤ε≤1,k: =0;
步骤2 令dk=-gk; 如果‖gk‖≤ε, 则停止;
步骤3 由一维搜索步长因子α, 使得
步骤4 计算xk+1=xk+αdk;
步骤5k∶=k+1, 转步骤2。
1.3 梯度下降法直接拟合光谱吸收信号过程

(4)
式(4)中,It=I0e-PSLxφ(ν), 通常可以写为关于时间的低阶多项式, 可将其写为三次多项式[11], 如式(5)所示
I0=C0t3+C1t2+C2t+C3
(5)
众所周知, 激光器的发射频率受材料、 电流和温度影响[12]。 对于分布反馈式激光器, 在温度不变时, 可以认为线性变化的电流在一定扫描范围内引起波长的线性变化[13]。 采用高精度锯齿波可以实现波长的精确扫描, 波长随时间的变化关系可以表示为式(6)
ν(t)=C4t+C5
(6)

(7)
损失函数L(θ)中, 向量θ包括了八个未知参量, 即C0,C1,C2,C3,C4,C5,C6和气体浓度x。 在应用梯度下降法前, 需对八个参量分别求偏导。 最后, 根据2.2节所述的梯度下降法, 每次迭代更新参数
(8)
其中θj是未知参量, 每一次迭代对八个参量同时分别更新。
梯度下降法直接拟合光谱吸收信号过程的流程图如图1所示。
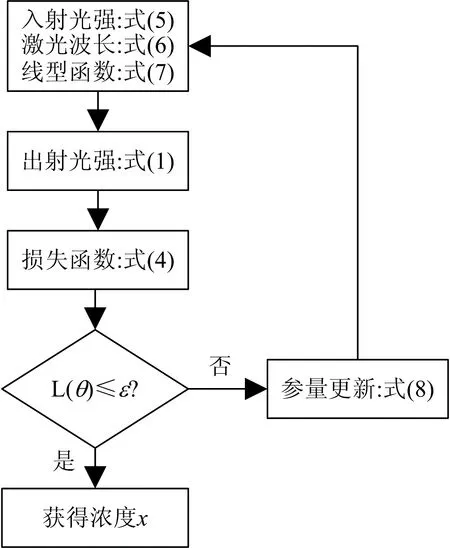
图1 拟合流程图
拟合过程在以下三个前提下进行: (1)激光器的发射信号可以用三阶式来描述; (2)气体对激光的吸收线型用洛伦兹线型描述; (3)在高精度锯齿波扫描下, 出射激光频率与电流呈线性关系。 当以上三个条件改变时, 需要对拟合的迭代公式做出相应调整。
2 实验部分
为验证基于梯度下降法直接拟合光谱吸收信号的气体浓度测量方法的准确性, 本文采用TDLAS实验系统进行CO2浓度测量[4], 如图2所示。 用流量控制仪(D08-2F, 七星华创)调节N2和CO2气体流量以配置不同浓度的CO2气体, 两种气体用混合器充分混合后通入气体池。 选用中心波长为1 580 nm的分布反馈式激光器(Distributed-feedback, Nanoplus)作为光源, 由激光控制器(PCI-1DA, Port City Instruments)控制激光器的电流和温度, 出射激光经过光纤准直器(F220FC-1550, Thorlabs)进入光程长度为2 000 cm的赫里奥特池, 经多次反射后由光电探测器(SM05PD5A, Thorlabs)将光信号转变为电信号, 再经过前置放大器放大后返回激光控制器, 采集的信号由PC上控制器软件读取, 采集频率为10 kHz。

图2 实验系统图
通过查阅HITRAN光谱参数数据库可知, 在波长1 580 nm附近有两条CO2的强吸收线, 均在10-23量级, 其光谱参数如表1所示。 可见Line2的吸收线强比Line1的吸收线强更强, 故拟合时选择Line2。 在温度25 ℃, 压力101.325 kPa的环境条件下, 用CO2和N2配置CO2浓度为10%, 12%, 14%, 16%, 18%和20%的六种混合气体, 将混合气分别通入气体池, 测量CO2对激光的吸收。

表1 CO2在1 580 nm附近两条吸收谱线的光谱参数(296 K)
3 结果与讨论
根据2.2节所述的梯度下降法基本原理, 给定的初始值越接近真实值, 迭代的速度越快, 迭代也越不容易发散, 因此初始值的赋值至关重要, 有必要对初始值如何赋值做出说明。
对入射激光强度中的四个参数C0,C1,C2,C3赋值, 方法为: 在采集的数据中选取四个未吸收区域采样点, 如图3所示。 选取的分别是第一个(No.1)、 第十个(No.10)、 倒数第十个(No.-10)、 最后一个采样点(No.-1)的数据, 将其代入式(5)计算。 根据四个未知数和四个公式, 可以得到一组C0,C1,C2,C3, 将这四个值作为C0,C1,C2,C3的初始值。
ν(t)中的C4和C5通常在实验前对激光器的性能测试实验中得到近似值作为迭代初始值, 但在本实验中没有使用标准具, 因此通过吸收光谱的两个吸收峰来确定波长与采样点之间的关系, 从而获得C4和C5的值。
对洛伦兹线型下的碰撞展宽, 有: 2C6=Δνc=P∑xA2γB-A, 式中,P为总压强,xA为组分A的体积分数,γB-A为组分A和B之间的展宽系数。 对于常温常压下的气体, 2γ≈0.1 cm-1·atm-1[14], 在未知Δνc的情况下, 可以取为0.1 cm-1, 故C6的初始值可以赋值为0.05。

图3 入射激光强度参数初值计算选点
确定目标气体浓度x的初始值, 有两种方式, 一种是利用对被测量气体的经验给出一个接近的初始值; 另一种方式是对于被测气体完全未知的情况下, 可以直接将其赋值为50%。 因为本研究的工况是模拟电厂烟道中CO2浓度, 在此应用场景下CO2浓度在10%~20%之间, 所以可以将迭代初始浓度设置为15%。
此外, 在迭代之前还需要确定步长因子, 采用CO2浓度10%的数据计算, 比较了五种步长因子迭代50次的拟合方差, 如图4所示。 其中, 步长因子为0.1时收敛速度最快, 因此选择0.1作为步长因子。 同时, 从图4上还可以看出, 迭代开始阶段, 拟合方差迅速降低, 说明所用方法收敛速度很快。

图4 五种步长因子的收敛速度
确定步长因子后, 对实验数据进行迭代计算。 采集了25 ℃下六种CO2浓度的吸收光谱信号, 为了提高吸收区域的拟合效果, 删除了低吸收区域四分之三的采样点之后再进行初始值赋值, 最后通过对数据的迭代获得气体的浓度信息。
迭代30步后, 得到如图5所示的拟合效果图, 其中图5(a)—(f)分别是浓度为10%, 12%, 14%, 16%, 18%和20%的拟合结果。 采集的数据点、 拟合开始位置、 迭代之后的数据曲线在图中标示, 蓝色实线为采样数据点, 绿色实线为拟合初始位置, 红色虚线为拟合得到的数据点。 其中, 拟合的数据点和采集的数据点基本重合, 残差在-0.035~0.015之间, 可以直观地看出应用梯度下降法可以很好地对光谱吸收信号进行拟合。

图5 不同浓度下拟合结果
由上述拟合结果得到直接拟合法更详细的数据, 如表2所示。 可以看到, 拟合计算浓度的相对误差在0.9%~4.4%之间, 同时六种浓度下拟合的方差均在1×10-4以下, 此时迭代时间在4 s以内。 以标准差的三倍来计算检测限, 检测限为0.39%。 利用积分面积法得到的CO2气体浓度值和相对误差也在表2中列出, 与直接拟合法进行对比, 积分面积法的平均相对误差为5.74%, 直接拟合法的平均相对误差为2.63%, 在本实验条件下直接拟合法的结果优于积分面积法。

表2 直接拟合法与积分面积法分析结果
对以上直接拟合法分析性能优于积分面积法的原因进行分析, 绘制出了在常规基线拟合法下得到的不同浓度的吸光度, 如图6所示。 可以看到, 积分面积法在做基线拟合时会出现吸光度小于0的情况, 这是积分面积法误差的主要来源。

图6 常规基线拟合得到的不同浓度下的吸光度
4 结 论
将基线、 气体浓度、 吸收线型等作为未知量, 通过建立光谱吸收信号的数学模型, 结合梯度下降法, 分别对10%, 12%, 14%, 16%, 18%和20%浓度的CO2吸收后的激光透射信号进行了拟合。 结果显示: 采用直接拟合法计算的浓度最小相对误差仅为0.90%, 平均相对误差为2.63%, 同时六种浓度下的拟合方差均小于1×10-4。 而积分面积法浓度反演的最小相对误差为4.10%, 平均相对误差为5.74%, 本工作所提出的基于梯度下降法直接拟合光谱吸收信号的气体浓度测量方法优于积分面积法, 进一步表明了该方法在气体浓度测量时的可行性与准确性。

