改进团队进步算法的近红外光谱波长筛选

高美凤， 陶焕明

江南大学轻工过程先进控制教育部重点实验室， 物联网工程学院， 江苏 无锡 214122

引 言

近红外光谱分析技术凭借其快速、 无损以及低成本的特点， 已经广泛运用在食品分析、 生物医学、 农业等领域。 但由于近红外光谱不同的波长点对被测物质不同化学基团的吸收强度不同， 被测物质浓度并不与光谱全谱波长信息相关， 往往采集到的全光谱数据存在大量的冗余信息以及噪声信息， 与之直接相关的有效信息仅仅存在于全谱信息中的一部分。 如何快速有效地提取出有用光谱信息是近红外光谱技术研究的重点之一。

目前， 国内外研究学者提出大量基于不同原理策略的波长筛选方法， 主要有： 以全谱PLS模型的某些参数作为变量选择的依据， 如无信息变量消除法(UVE)对回归系数设定阈值限制来选择有效变量[1]； 以光谱区间为筛选对象的方法， 如区间偏最小二乘(iPLS)[2]、 移动窗口偏最小二乘(MWPLS)[3]、 向前和向后间隔偏最小二乘(FB-iPLS)[4]、 区间随机蛙跳(iRF)[5]等； 以连续投影策略进行变量排序筛选出最优变量子集， 如连续投影算法(SPA)[6]； 以模型集群分析策略的方法， 如变量空间迭代收缩(VISSA)[7]、 变量组合集群分析(VCPA)[8]； 以智能算法为核心进行波长组合优化， 如遗传算法(genetic algorithm， GA)[9-11]、 免疫遗传算法(IGA)[12]、 粒子群算法(PSO)[13]、 蚁群算法(ACO)[14]、 二进制蜻蜓算法(BDA)[15]等。 团队进步算法(team progress algorithm， TPA)[16-17]是一种典型的智能组合优化算法， 它是通过树立榜样引导团队进步的方向， 利用合理的分工合作提高工作效率。

近红外光谱波长变量多， 需要在多达几百甚至上千的波长点中， 选择最有效的波长点， 使得所建模型的预测精度最高， 因此将波长筛选问题转化为波长点之间的组合优化问题， 通过智能组合优化算法寻找光谱中的最佳波长。 在团队进步算法的基础上， 提出一种应用于近红外光谱波长筛选的智能组合优化算法： 改进团队进步算法(improved team progress algorithm， iTPA)。 首先将波长变量均分为若干波段， 对波段按照与其相应的理化值进行PLS建模， 将得到的评价值函数按大小降序排列， 波段分组中增设一个垃圾回收组。 按评价值从高到低依次分为精英组、 普通组和垃圾回收组， 建立精英组和垃圾回收组两个学习样板， 结合学习和探索的过程， 通过不断的迭代更新， 选取评价值最高的波段作为筛选波段。 该算法在计算迭代过程中， 每个波段的波长点在不断进行更新， 各小组在搜索过程中出现明显的分工， 使算法具备良好的全局搜索能力。

1 算法原理及实现

1.1 TPA算法实现原理

1.1.1 数学模型

TPA是一种双群体搜索算法[16]， 模仿团队两个小组(精英组和普通组)的学习和探索过程， 并设计合理的成员更新规则， 逐步提升其评价值以达到全局最优。 实验表明， 该算法能够在较少的计算量前提之下快速寻找全局最优。

算法模型多变量无约束最大化问题可表示为

(1)

式(1)中， 向量x代表一个成员， 即为包含多个波长的波段；xi表示该成员的第i个能力因素， 即该波段中的第i个波长点；ai和bi分别表示xi的上下边界值； 而函数f(x)代表该成员x的评价值。 通过更新成员以逐步提升或降低评价值来寻求最优成员。

1.1.2 分组规则

将整条光谱波段均分为P个波段同时确定其评价值， 评价值为该波段与测得的含量理化值进行PLS建模得到的校正集均方差(RMSEC)和相关系数(r)为变量的函数值， 本工作设定的评价值为

(2)

每一个波段就相当于向量x。 将P个波段按评价值从大到小排列分成N+M个波段(N和M均为整数)，N个评价值较高的波段组成精英组{xe1,xe2, …,xen}，M个评价值较低的波段组成普通组{xp1,xp2, …,xpm}。 通过团队进步过程更新组内成员。

1.1.3 行为定义

需要产生一条新生波段xr， 新生波段可从任意一组产生， 其波长点从当前组随机波段同一波长点中继承。 若新生波段出身自精英组， 且该新生波段的第i个波长点如果是在精英组第n个波段中产生， 那么该波长点需继承精英组第n个波段中第i个波长点； 若新生波段出身自普通组， 且该新生波段的第i个波长点如果是在普通组第m个波段中产生， 那么该波长点需继承普通组第m个波段中第i个波长点。 继承下来的新生波段通过设定概率选择一次学习或者探索行为以更新自身的波长点， 才能成为候选波段xc。

新生成员xr如果选择进行学习行为， 则需要向参照目标方向调节。 参照方向产生于精英组和普通组， 分别称为精英组样板ee和普通组样板ep， 且样板值取所在组波段波长的平均值。 若新生波段产生于普通组， 则其需向精英组样板调节； 若新生波段产生于精英组， 则向普通组样板的反方向调节， 如式(3)所示。

(3)

式(3)中，γ为区间[0, 1]内随机数。 若xc某个波长点范围越界， 则改用其边界值。

新生成员如果进行探索行为， 则其各波长点xri(i=1, 2, …,n)将做随机改变。 并且探索强度逐步减小。 两组新生波段xr经过探索行为生成xc的表达式如式(4)和式(5)所示。

xc=[xc1,xc2, …,xcn]T

(4)

(5)

式(5)中，γi是区间(0, 1)的随机数，mi为0和1二值随机整数。 收缩系数te, p为

(6)

式(6)中，K为算法最大迭代次数，k表示当前累计的迭代次数。 收缩指数αe, p表示当新生波段继承自精英组时选取αe， 当新生波段继承自普通组时选取αp。

1.1.4 更新规则

若候选波段xc的评价值高于精英组末位xewst的评价值， 则xc进入精英组， 同时精英组再次进行评价值排序， 精英组末位xewst不进入普通组直接淘汰。 这是因为TPA设置了学习行为， 加强了算法的定向搜索和局部搜索能力， 遭到淘汰的精英组末位xewst如果进入普通组的话容易导致算法陷入局部最优。 若候选波段xc的评价值劣于xewst但优于普通组末位xpwst， 还需检查xc是否由探索行为得到， 若是， 则xc进入普通组， 淘汰xpwst。 若不是， 直接丢弃xc。 这是因为学习行为产生高评价值候选波段的可能性比较大， 且趋同性强， 容易导致普通组波段同化， 降低全局寻优能力。

1.2 改进TPA算法

在TPA算法中， 继承于精英组的新生波段xr在选择学习行为时， 需要向普通组样板ep的反方向调节。 但在迭代过程中， 精英组和普通组的成员在不断进行更新优化， 从而在迭代后期， 普通组的样板值ep也随着精英组样板值增大， 在选择学习行为时， 并不能为继承于精英组的新生波段xr提供一个良好的调节方向， 容易陷入局部最优。 因此对TPA算法进行如下改进：

1.2.1 改进分组规则

在对P个成员进行分组时， 由原来的N+M模式改为N+M+L模式， 评价值依次降序排列。N为评价值高的波段组成的精英组{xe1,xe2, …,xen}，M为评价值适中的波段组成的普通组{xp1,xp2, …,xpm}， 新增添的L组为评价值最低的波段组成的垃圾回收组{xg1,xg2, …,xgl}。 再通过团队进步过程更新成员。

1.2.2 学习行为重定义

新增添的L组不参与继承、 学习以及探索行为。 新生波段进行学习行为时， 仍需要向参照目标方向调节， 参照方向更改为分别产生于精英组和垃圾回收组， 称为精英组样板ee和垃圾回收组样板eg， 样板值依旧取所在组波段波长的平均值。 即若新生波段产生于普通组， 则其需向精英组样板调节； 若新生波段产生于精英组， 就向垃圾回收组样板的反方向调节， 如式(7)所示。

(7)

式(7)中，γ为区间[0, 1]内随机数。 若xc某个波长点范围越界， 则改用其边界值。

1.2.3 更新规则的修改

在进行波段更新的时候需要将低评价值的波段回收进L组， 使L组的波段评价值极低。 新的波段更新规则在精英组和普通组不做修改， 当候选波段xc的评价值低于垃圾回收组首位(垃圾回收组中评价值最高)xgbst的评价值， 则xc进入垃圾回收组， 同时垃圾回收组中的xgbst波段遭到淘汰， 促使垃圾回收组评价值一直保持低的状态， 为继承于精英组的新生波段进行学习行为时提供一个正确的更新方向， 有效地避免算法陷入局部最优。

1.3 iTPA算法实现步骤

Step1： 初始化基本参数。 包含总波段成员个数， 精英组、 普通组以及垃圾回收组的波段个数， 新生波段选择学习或探索行为的概率， 精英组和普通组的收缩系数， 迭代次数。

Step2： 分组。 将各波段按照与其相应的理化值PLS建模得到的评价值函数大小降序排列， 评价值函数如式(2)所示， 依次放入精英组、 普通组和垃圾回收组， 使得精英组中评价值最高， 普通组次之， 垃圾回收组最低。

Step3： 产生新生波段。 新生波段随机选择从精英组或普通组中产生， 其波长点从当前组随机波段同一波长点中继承。

Step4： 新生波段选择学习或探索行为生成候选波段。 生成一个随机数， 若随机数满足选择学习行为的概率， 则需进行学习行为。 在进行学习行为之前， 需判断该新生波段是从精英组还是普通组产生， 以便选择不同的学习行为， 如式(7)所示。 若随机数满足选择探索行为的概率， 则需进行探索行为。 在进行探索之前， 仍需判断该新生波段是从精英组还是普通组产生， 从而为探索行为选择不同的收缩系数， 如式(5)和式(6)所示。 若行为过程中某个波长点范围越界， 则改用其边界值。

Step5： 波段更新。 候选波段的评价值需要跟三个小组中的波段评价值进行对比更新。 更新规则参阅本文1.1.4和1.2.3。

Step6： 循环Step3—Step5进行迭代更新。 迭代结束， 选出精英组中评价值最高的波段为最终筛选波段。

2 实验部分

2.1 数据准备

2.1.1 数据来源

为考察新提出的变量筛选算法对建模预测的效果， 将其应用在一组标准玉米近红外光谱数据集。 该光谱数据集引用自eigenvector网站上开源的玉米样本光谱数据集， 网址https://eigenvector.com/resources/data-sets/。 该数据集为80个玉米样品用mp5spec仪器扫描得到的光谱数据， 并用化学方法测定了其淀粉和蛋白质含量。 以间隔为2 nm在波长范围为1 100～2 498 nm上收集(700个波长点)。

2.1.2 剔除异常数据及样本划分

考虑到仪器测量光谱数据时因误差而得到异常光谱， 会影响模型性能， 故先用马氏距离剔除光谱中异常数据。 图1为各个数据样本点到数据中心点的马氏距离分布图。 马氏距离最远的两个样本(75和77号样本)作为异常点剔除， 图2为剔除异常样本之后的原始光谱图。

图1 样本马氏距离分布图

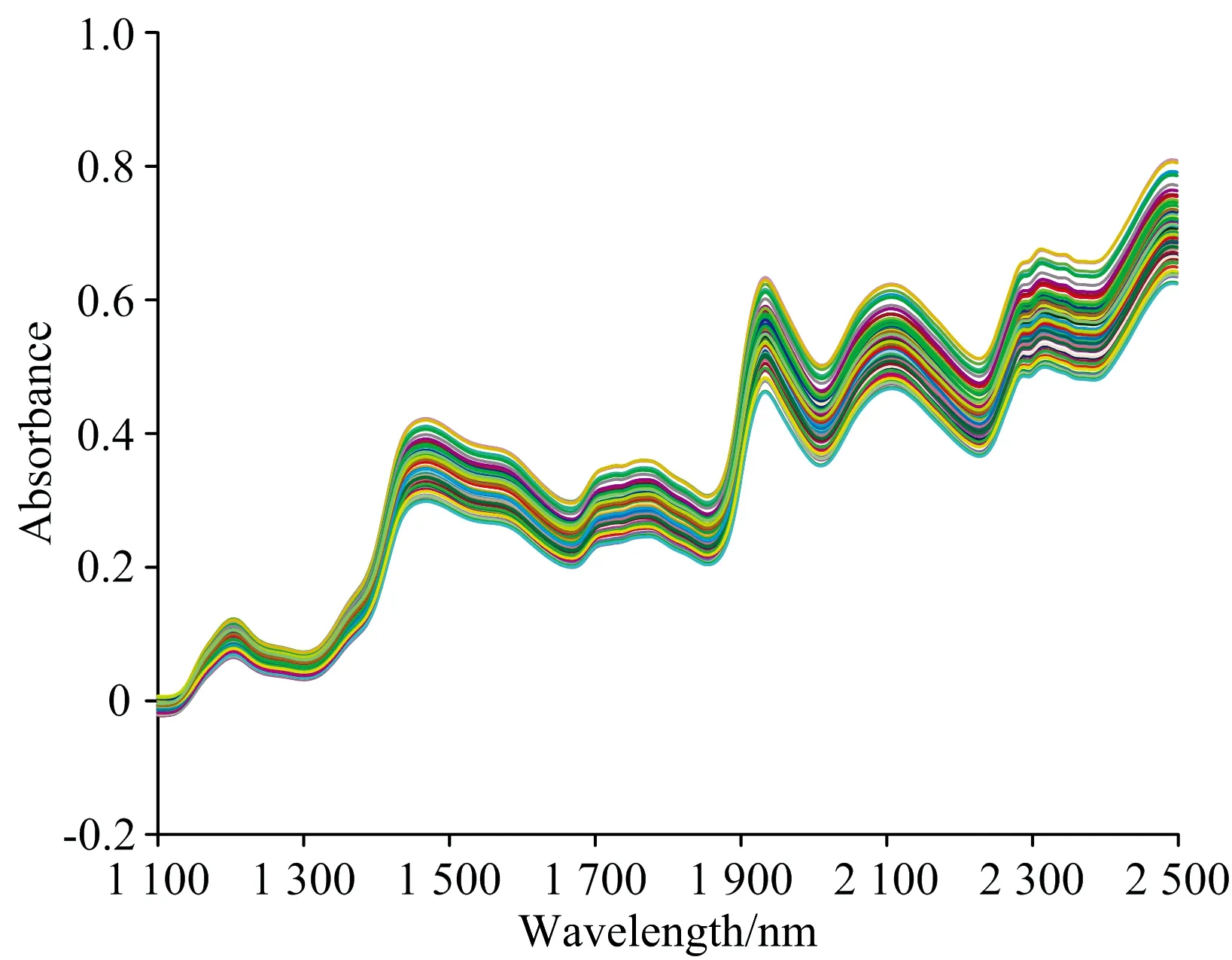
图2 剔除异常样本的光谱图

采用Kennard-Stone(KS)方法[18]将剩余的78个样本点分成校正集和预测集。 划分结果为校正集样本50个， 预测集样本为28个。 校正集和预测集淀粉和蛋白质含量值统计如表1。 由表1可知， 校正集样本与预测集样本的平均值和标准差相差不大， 通过KS方法划分数据集保证了校正集样本均匀分布。

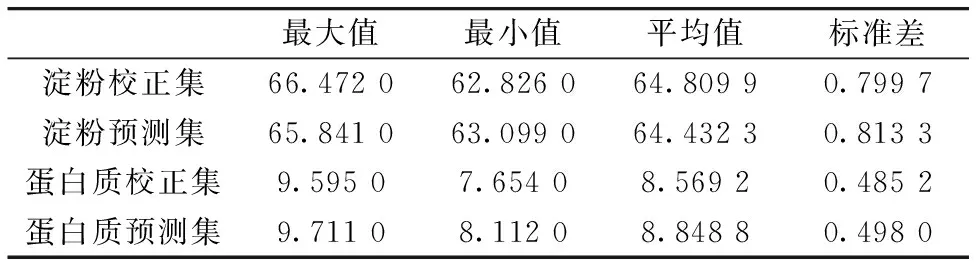
表1 校正集和预测集中淀粉和蛋白质含量值g/100 g统计

2.2 方法

实验使用的是一台戴尔计算机， 处理器是Intel(R) Core i5-9400， CPU主频为2.90 GHz， 操作系统为Windows10，所有计算均在MATLAB 2016a中进行。 为了验证iTPA算法的有效性和优越性， 分别用全谱波长、 GA、 TPA以及主成分分析(principal component analysis， PCA)算法对玉米的淀粉和蛋白质含量的建模效果进行了对比。 进行GA算法时， 由于原始光谱波长点数众多， 如对波长点进行优选组合， 运算效率将会非常低， 因此将原光谱均分若干个子区间， 用GA算法进化迭代获取最大适应度值所对应的优选子区间组合。 根据基因选出的波段建立PLS模型， 计算出模型的相关系数(r)和校正集预测均方根误差(RMSEC)， 适应度函数F跟iTPA算法评价值函数f(x)保持一致为

(8)

将原光谱在1 100～2 498 nm范围之间共700个波长点数划分35个等距区间， 即遗传编码长度为35， 每一个基因包含20个波长点数。 设定群体个数为50个， 交叉概率为0.85， 变异概率为0.1， 最大迭代数为200代。 在种群进化过程中寻找最大迭代次数内进化过程中最优适应度个体。

同样的， 采用TPA算法时将原光谱等分35个波段区间， 每个波段内含20个波长点数， 即每个成员对应20个能力因素。 按照算法经验， 精英组由15个波段组成， 普通组由20个波段组成， 该分组模式算法性能最优。 设定选择学习概率为0.35， 循环尝试不同的收缩指数， 当精英组收缩指数为20时， 算法预测效果最优， 普通组收缩指数设定为精英组的0.5倍。 迭代次数为1 000。 迭代完毕之后， 取精英组评价值最高的成员为优选成员， 优选成员中包含的能力因素就是所要筛选的波长点。 如出现重复波长点则去除即可。 因此， 采用TPA算法筛选出来的波长点数最多不超过20个。

对于iTPA算法， 同样分为35个成员， 按照算法经验， 其中精英组10个成员， 普通组10个成员， 垃圾回收组15个成员， 该分组模式算法效果最优， 其余设定条件与原TPA算法保持一致。 由于GA算法、 TPA算法、 iTPA算法都具有的随机性， 因此将以上三种算法分别运行50次求平均。

3 结果与讨论

3.1 算法性能分析

改进算法iTPA优化了TPA算法的更新方向， 促使算法很大程度上避免陷入局部最优。 图3为用TPA和iTPA筛选之后的变量分别与淀粉和蛋白质含量测试50次进行建模分析的预测均方根误差值。

由图3可知， iTPA算法由于避免了陷入局部最优， 使得整体预测效果得到了明显的提升。 表2和表3分别为各算法测试淀粉含量和蛋白质含量的各项性能数据。

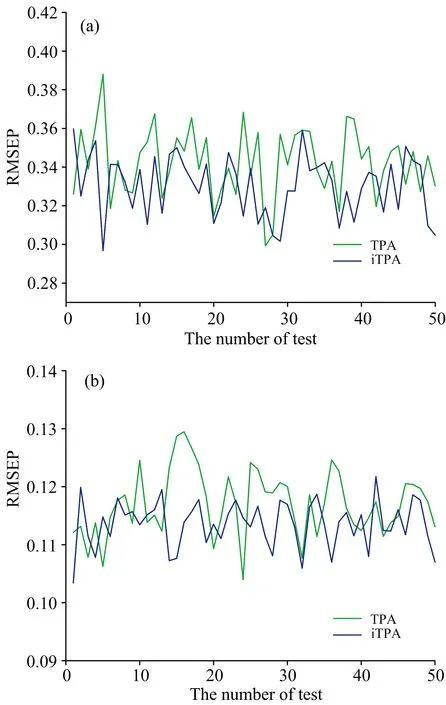
图3 TPA和iTPA算法运行50次(a)淀粉预测RMSEP值和(b)蛋白质预测RMSEP值

表2 不同变量筛选方法对玉米淀粉含量的预测结果

从表2可得， 在玉米淀粉含量的预测上， iTPA相比于全谱PLS(F-PLS)， 变量个数从700个减少到均值为17.55个(50次运算求平均)， 模型的校正均方根误差RMSEC从0.335 7降到0.260 9左右， 校正集预测精度提升22.3%。 模型的预测均方根误差RMSEP从0.391 4下降到0.334 4左右， 预测集预测精度提升14.6%。 相比原TPA算法有了提升， TPA算法的RMSEP为0.345 3。 GA算法总体预测效果是最佳， 但其筛选出来的平均波长点数高达350个和算法运算时间21.98 s， 远远大于iTPA算法的17.55个和0.676 s。 通过对原光谱进行PCA降维， 筛选出20个波长点(贡献率已达0.999 98)， 以此与筛选出近乎相同波长数的iTPA算法作比较。 经PCA算法筛选波长之后得到的RMSEP为0.792 7， 预测效果远不如iTPA算法。 因此， iTPA算法应用在淀粉含量光谱数据集中能在保持预测能力的前提下大幅度削减波长点数， 有效地减小建模的计算量， 同时算法速度更快。

表3 不同变量筛选方法对玉米蛋白质含量的预测结果

从表3可得， 对于玉米蛋白质的预测， iTPA算法预测均方根误差RMSEP为0.117 7， 预测相关系数Rp为0.970 4， 校正均方根误差RMSEC为0.101 9， 校正相关系数Rc为0.975 9， 预测效果比全谱PLS和原TPA算法都有提升， 全谱PLS的RMSEP为0.178 9， TPA算法的RMSEP为0.119 3。 GA算法总体预测效果最佳， 但其筛选出来的平均波长点数高达346个， 以及算法运算时间22.12 s， 远远大于iTPA的19.60个和0.666 s。 通过对原光谱进行PCA降维， 筛选出20个波长点(贡献率已达0.999 997)。 经PCA算法筛选波长之后得到的RMSEP为0.236 2， 预测效果远不及iTPA算法。 因此， iTPA算法应用在蛋白质含量光谱数据集中， 同样能在保持预测能力的前提下大幅度削减波长点数， 有效地减小建模的计算量， 同时算法速度更快。

3.2 化学特性分析

图4表示iTPA算法分别在玉米淀粉和蛋白质数据集上运行50次后变量被选取的频率。

由图4(a)可知， 淀粉近红外光谱被iTPA算法筛选后的信息变量区域主要分布在1 540～1 546， 1 576～1 588， 1 724～1 730和1 766～1 772 nm等区域， 而这些区域与淀粉中O—H的伸缩振动一级倍频以及C—H的伸缩振动一级倍频的频率一致， 这与本次研究中淀粉的化学性质相一致。

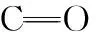
图4 iTPA算法运行50次后(a)淀粉光谱变量被选取的频率和(b)蛋白质光谱变量被选取的频率

因此iTPA算法能够有效地消除光谱信息中的一些干扰波长点， 达到筛选出有效波长点目的。

4 结 论

提出了一种近红外光谱波长变量选择算法， 即改进的团队进步算法(iTPA)， 对玉米淀粉和蛋白质的近红外谱波长进行选择， 建立了更加稳健的PLS模型， 模型的预测均方根误差RMSEP分别为0.334 4和0.117 7， 获得了满意的预测精度。 结果表明： iTPA与其他波长选择算法相比性能均有一定优化， 特别是筛选出的有效波长数目最少， 达到20个以下， 从而降低了模型的复杂度； 快速的寻优能力也有利于近红外光谱检测在工业现场的实时应用。