单向碳纤维复合材料板阻尼性能研究
吴鑫锐,颛孙晓岩,姚 荐,郭大虎,周 涛,董 斌,王时玉
(1.上海复合材料科技有限公司,上海201112;2.西北工业大学,陕西 西安710129)
引 言
本文通过实验模态分析技术和有限元模拟技术研究了碳纤维T700S增强阻尼改性环氧树脂复合材料单向板,不同纤维角度对单向板模态阻尼损耗因子及固有频率的影响。
1 阻尼损耗因子的计算
通过ANSYS有限元软件的模态分析不仅可以得到结构的固有频率和固有振型,还可以得到结构每个单元的应变能和每个单元六个方向的应力、应变。本文利用有限元模拟结果并采用应变能法计算结构各阶模态的阻尼损耗因子[1~3],具体计算过程如下所示:
在一个振动周期内,系统总耗散能与系统总应变能的比值称为系统的比阻尼容量,即:

式中:
△U—系统总耗散能;
U—系统总应变能。
系统阻尼损耗因子与比阻尼容量的关系是:

单元i的应变能为:
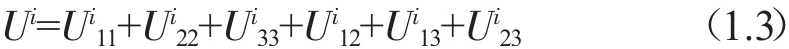
式中:Ujk为单元i各方向应变能。
系统的总的应变能为:

式中:n为系统总的单元数。
单元i的耗散能为:
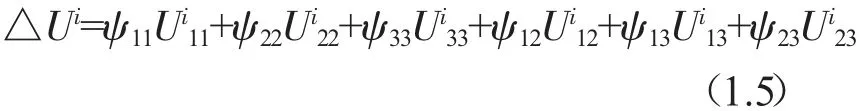
其中ψjk对应于应力σjk方向的比阻尼容量。
系统的总耗散能为:

对于层单元来说,单元i的应变能计算应该具体到每一铺层上,如下式所示:

式中:N—单元总层数;
Uip,j—单元i第ρ层各应力方向对应的应变能,具体表达式如下所示:

此时单元i耗散能表示为:
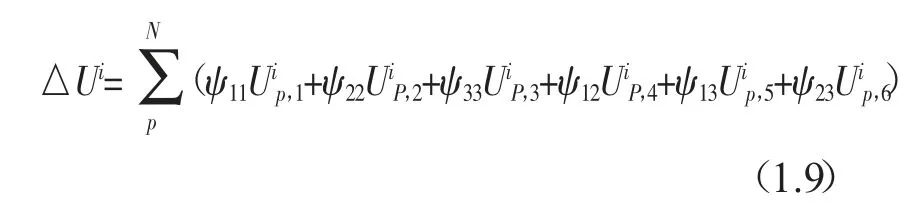
再通过式(1.4)、(1.9)可求出系统的比阻尼容量和阻尼损耗因子。
2 碳纤维复合材料各方向比阻尼容量的确定
由于T700S碳纤维复合材料是正交各向异性的,这就决定其阻尼性能也具有正交各向异性,以ψ11、ψ22、ψ33、ψ12、ψ13、ψ23表示复合材料六个方向的比阻尼容量,一般情况下认为ψ22=ψ33、ψ12=ψ13=ψ23,这样只需确定ψ11、ψ22和ψ12这三个量,便可得到材料六个方向的比阻尼容量。碳纤维复合材料单向0°、45°和90°复合材料的阻尼损耗因子随温度的变化已经测定,在温度为30℃,频率为1Hz的条件下,三种单向复合材料的阻尼损耗因子如表1所示。

表1 单向复合材料阻尼损耗因子(30℃,1Hz)Table 1 The damping loss factor of unidirectional composites(30℃,1Hz)
并根据阻尼损耗因子与比阻尼容量的关系,即ψ=2πη,可以得出三种单向复合材料在温度为30℃,频率为1Hz条件下的比阻尼容量,如表2所示。

表2 单向复合材料比阻尼容量(30℃,1Hz)Table 2 The specific damping capacity of unidirectional composites(30℃,1Hz)
其中ψ0即为沿纤维方向的应力σ1对应的比阻尼容量ψ11,而ψ90即为垂直于纤维方向的应力σ2对应的比阻尼容量ψ22,由于平面剪切应力τ12对应的比阻尼容量ψ12,进行实验测定比较麻烦,可根据文献[4~5]中R.D.Adams和M.R.Maheri以经典层合板理论为基础,推导出层合板比阻尼容量的计算公式,求出比阻尼容量ψ12。这样就得到了碳纤维复合材料六个方向的比阻尼容量,如表3所示。

表3 T700S碳纤维复合材料6个方向比阻尼容量(30℃,1Hz)Table3 The specific damping capacity of t700s carbon fiber composite in six directions(30℃,1Hz)
3 单向碳纤维阻尼复合材料板振动测试实验
制备T700S碳纤维复合材料的单向0°、45°和90°复合材料板,并利用实验模态分析中的锤击法测试每种板的前3阶纵向弯曲模态的固有频率,实验过程参考标准GB/T18258-2000。
3.1 试件参数与设备
制备0°、45°和90°单向复合材料振动测试试件,每种试件共铺设12层预浸料,单层预浸料的厚度为0.18mm,试件的尺寸如图1所示。

图1 振动测试试件的尺寸示意图Fig.1 The dimension diagram of vibration test specimen
采用模态分析设备为DEWETRON动态信号分析仪。
3.2 实验结果与分析
由于试件宽度很小,无法在横向方向上布置测试点,故通过振动实验只能得到单向0°、45°和90°复合材料板的前三阶纵向弯曲模态的固有频率,测试结果如表4所示。
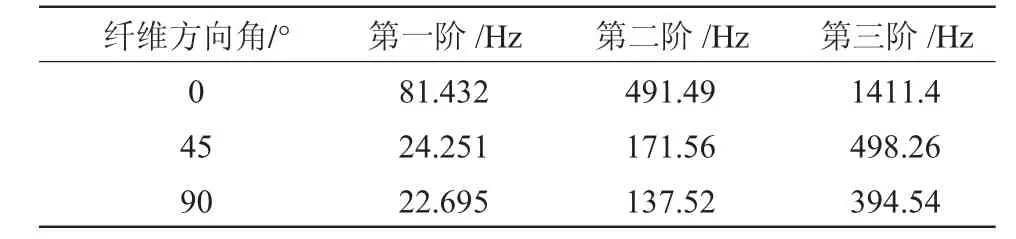
表4 各阶固有频率实验值Table 4 The experimental values of natural frequencies
从表4中可以得到同一阶模态中,随着纤维方向角度的增加,固有频率随之降低,并且降低的幅度会逐渐减小,这是由于随着纤维角度的增加,结构的整体刚度会随之下降,所以固有频率会逐渐降低。
4 有限元模拟分析
用ANSYS有限元软件模拟分析单向0°、45°和90°复合材料板的固有频率,将得到的模拟值与实验值进行比对,并以此模型分析纤维方向角对单向板前四阶模态阻尼损耗因子和固有频率的影响。
4.1 有限元模拟分析过程
ANSYS有限元模拟分析过程分为建立几何模型、设定参数、建立有限元模型、设定边界条件与求解和查看结果这五个步骤[6]。T700S碳纤维复合材料的参数如表5所示。

表5 T700S碳纤维复合材料参数Table 5 The parameters of t700s carbon fiber composites
4.2 模拟结果与实验结果的对比分析
在普通后处理器POST1中得到了单向0°、45°和90°复合材料的前三阶纵向弯曲的固有频率,并与实验结果进行了对比,如表6所示。
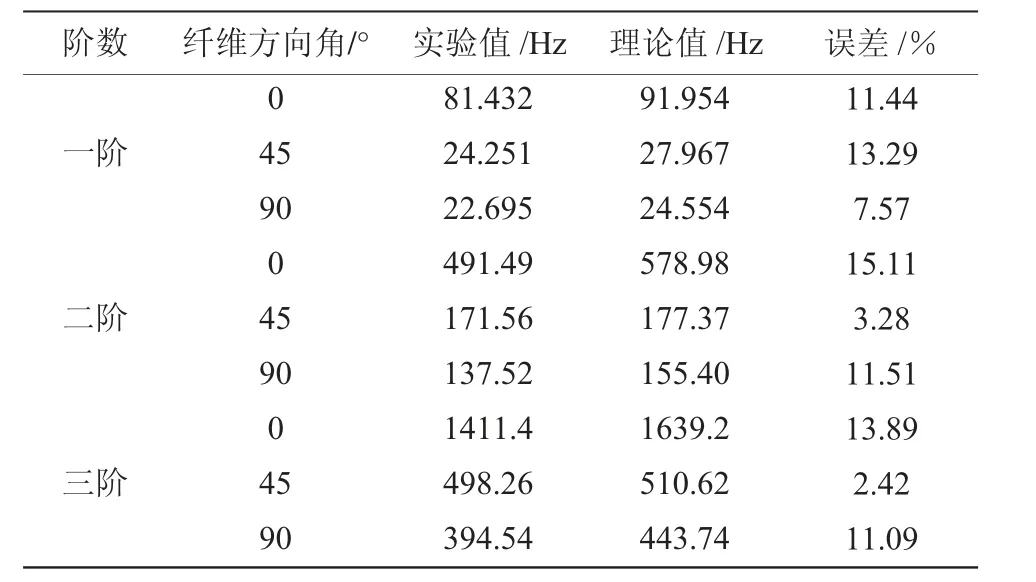
表6 前三阶纵向弯曲固有频率的实验值与有限元模拟值Table 6 The experimental and finite element simulation results of the first three longitudinal bending natural frequencies
从表6中可以看出,前三阶纵向弯曲固有频率的有限元模拟值与实验值吻合得很好,这证明建立的有限元模型可以很好地反应结构的固有属性,可用此模型继续讨论纤维方向角对材料固有频率和模态阻尼损耗因子的影响。
有限元模拟值与实验值存在一定的偏差,有以下几方面的原因:
(1)由于试验件的质量很轻,会受到加速度传感器附加质量的影响,因为整体质量变大,固有频率会变低,从表中可以看到实验值均低于模拟值,所以附加质量对固有频率的影响很大;
(2)在实验中虽然将试件一端固定住,但和理想悬臂梁的边界条件还是有差异的,这也会造成一定的误差;
(3)仪器设备造成的误差;
(4)其他因素的影响,如周围环境的温度、噪音、湿度、辐射、电磁场等。
4.3 纤维方向角对复合材料板阻尼性能的影响
利用上述的有限元模型模拟分析了不同纤维角度的单向复合材料板前四阶固有频率,分析结果如表7所示。

表7 不同纤维方向角的单向板前四阶固有频率Table 7 The first four natural frequencies of unidirectional plates with different fiber orientation angles
由表7可以绘制固有频率随纤维方向角变化的曲线图,如图2所示,从图中可以看出,第一阶、第二阶、第三阶固有频率随纤维角度的增加而逐渐降低,这是由于随着纤维角度的增加,试样整体刚度在逐渐下降,所以固有频率也逐渐下降。在15~30°区间下降速度较快,之后变化较为平缓,当角度达到75~90°时,固有频率已基本保持不变。第四阶固有频率在0~15°区间是增加的趋势,之后随纤维角度的增加而逐渐下降,变化的趋势逐渐平缓,这是由于0°单向板第四阶模态为扭转变形,而15°单向复合材料第四阶模态为纵向弯曲变形,如图4的(d)和(e)所示,弯曲刚度比扭转变形刚度大,所以固有频率有所上升,而15~90°单向复合材料的刚度逐渐降低,固有频率也随之降低。
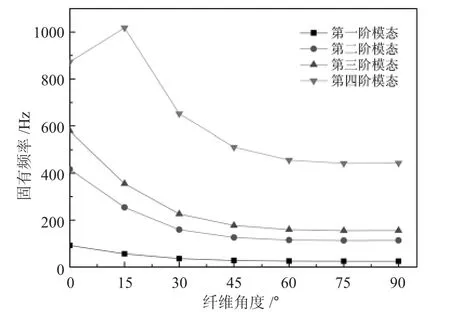
图2 固有频率随纤维方向角的变化Fig.2 The change of natural frequency with fiber direction angle
在后处理结果中还得到了每个单元的应变能、每个单元六个方向应力和每个单元六个方向应变。通过ANSYS参数化设计语言(ANSYS Parametric Design Language,缩写为APDL)编程,首先提取出每个单元的应变能并求和,再提取出每个单元每层中六个方向的应力和应变,计算出每个单元六个方向的应变能,将其累加得到整体每个方向的总应变能,最后应用应变能法计算出不同纤维角度单向复合材料板的前四阶模态阻尼损耗因子。
通过编程计算得到了不同纤维方向角单向板的前四阶模态阻尼损耗因子,结果如表8所示。
由表8可以绘制模态阻尼损耗因子随纤维方向角变化的曲线图,如图3所示,从图中可以看出前三阶模态阻尼损耗因子随纤维角度的变化趋势基本相同,纤维角度0~15°阻尼损耗因子增加,从15~45°阻尼损耗因子增加的速度逐渐变小,在纤维角度45°时达到最大值,随着纤维角度的增加阻尼损耗因子缓慢的降低。而第四阶模态阻尼损耗因子在0°时达到最大值,之后从15~90°的变化趋势与第一阶、第二阶、第三阶模态阻尼损耗因子基本相同。

表8 模态阻尼损耗因子随纤维方向角的变化Table 8 The variation of modal damping loss factor with fiber direction angle

图3 模态阻尼损耗因子随纤维方向角的变化Fig.3 The variation of modal damping loss factor with fiber direction angle
本文通过分析结构阻尼耗散机理来解释单向碳纤维增强复合材料板模态阻尼损耗因子随纤维方向角的变化曲线,由于复合材料层合板结构受力时,可以产生扭转或弯曲变形,不同的变形结构的阻尼损耗因子是不同的,也就是说模态损耗因子的值主要取决于各阶模态,通过分析已得到0~90°单向复合材料前四阶的固有振型,其中0~90°前三阶的固有振型是一致的,如图4的(a)、(b)、(c)所示,第一阶为纵向弯曲模态,第二阶为横向弯曲模态,第三阶为纵向弯曲模态,单向0°复合材料的第四阶振型为扭转模态,如图4的(d)所示,单向15~90°复合材料的第四阶振型为纵向弯曲模态,如图4的(e)所示。

图4 不同纤维角度单向复合材料板的前四阶模态Fig.4 The first four modes of unidirectional composite plates with different fiber angles

由应变能法可知,结构损耗因子取决于材料六个应力方向应变能占总应变能的比例以及相应方向的比阻尼容量。定义结构总应变能为U,总耗散能为△U,各应力方向对应的应变能为U11、U22、U33、U12、U13、U23,各应力方向对应的耗散能为△U11、△U22、△U33、△U12、△U13、△U23,为了比较各个应力分量对阻尼贡献量的大小,定义:

通过有限元模拟得到了不同纤维方向角层合板在不同模态下各个应力分量对阻尼的贡献情况,如图5所示。
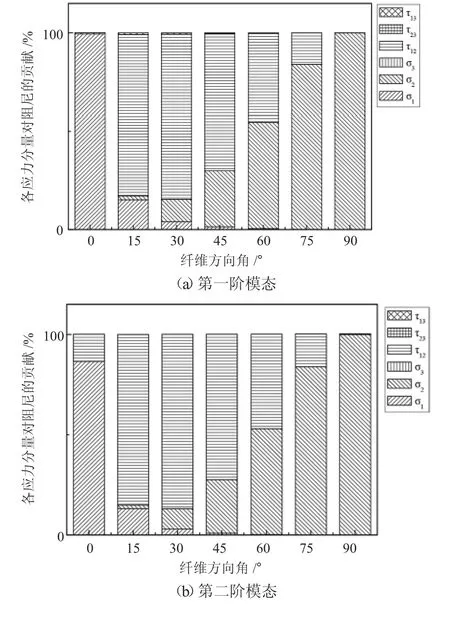
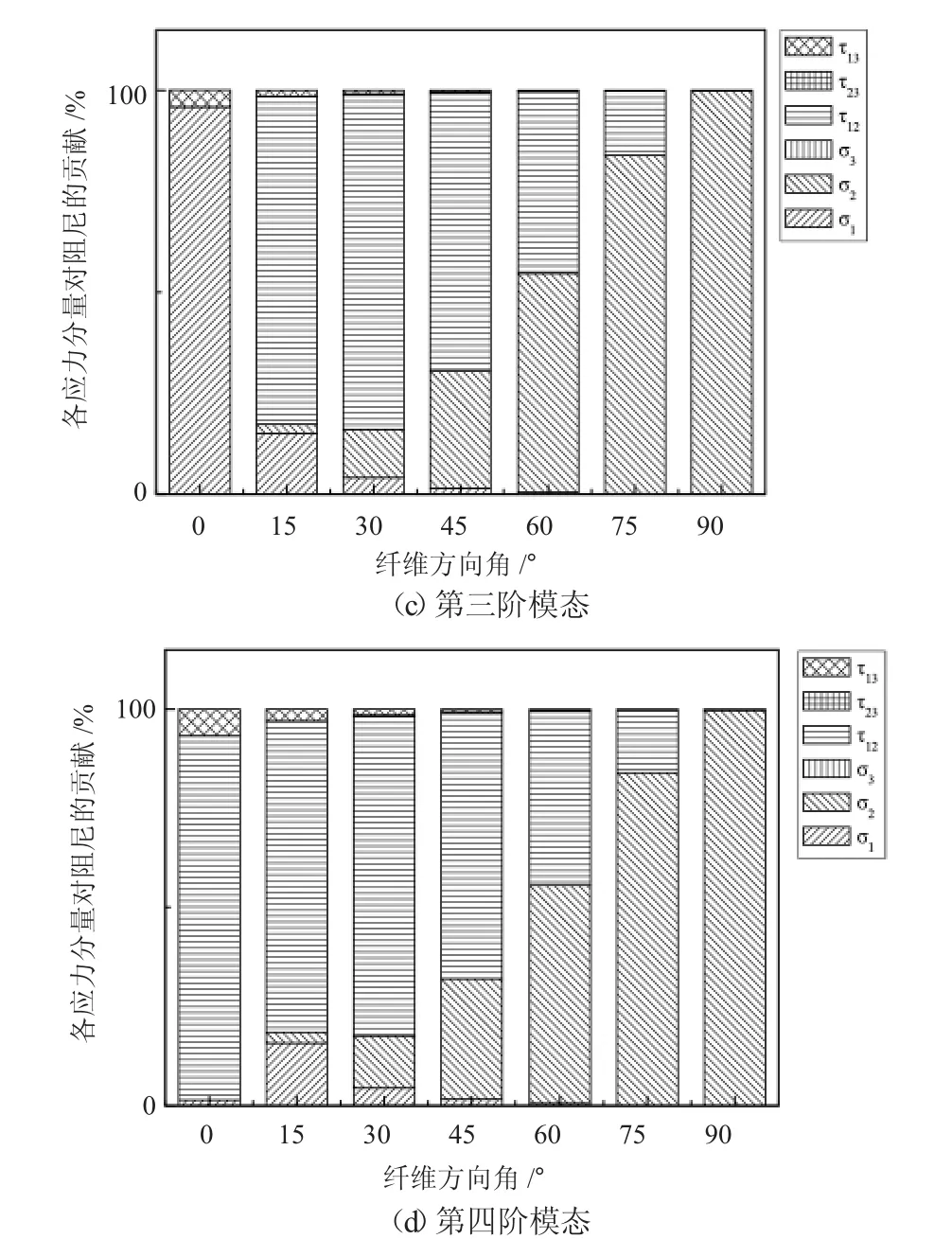
图5 不同模态下各个应力分量对阻尼的贡献Fig.5 The contribution of each stress component to damping in different modes
从图中可以看出在不同模态下各个应力分量对阻尼的贡献主要来自于沿纤维方向的应力σ1、垂直于纤维方向的应力σ2和面内剪切应力τ12。前三阶模态均属于弯曲模态,在纤维方向角为0°时对阻尼的贡献主要来自于沿纤维方向的应力σ1,因为σ1方向的比阻尼容量较低,故整体结构的阻尼损耗因子较低。当纤维方向角为15°时,对阻尼起主要作用的是面内剪切应力τ12,由于面内剪切应力对应的比阻尼容量高,所以整体结构的阻尼损耗因子快速提高。纤维方向角从15~45°,面内剪切应力τ12对阻尼的作用是先增加再下降,在纤维方向角为30°时达到最大,而垂直于纤维方向的应力σ2的作用在不断提高,在两者共同的作用下,在纤维方向角为45°时,整体结构的阻尼损耗因子达到最大,并且应力σ2对应的比阻尼容量比应力τ12对应的比阻尼容量小,所以纤维方向角从15~45°,整体阻尼损耗因子的增长速度在逐渐变缓。纤维方向角从45~90°时应力σ2的作用还在不断提高,而应力τ12的作用一直在减小,当纤维方向角为90°时,主要作用均来自于应力σ2,应力τ12贡献量已变得很小,并且应力σ2对应的比阻尼容量比应力τ12对应的比阻尼容量小,所以从纤维方向角从45~90°,整体的阻尼损耗因子在缓慢地降低。
当纤维方向角为0°时,第四阶模态为扭转模态,此时对阻尼的贡献主要来自于面内剪切应力τ12,又由于应力τ12对应的比阻尼容量高,所以整体的阻尼损耗因子达到最大,之后纤维方向角从15~90°第四阶模态变为弯曲模态,整体阻尼损耗因子随纤维方向角的变化与前三阶模态相似,机理也与前面分析的一样。
通过以上的分析,可以得出面内剪切应力对整体结构的阻尼性能影响是最大的。
5 总结
本文以T700S碳纤维复合材料预浸料制备0°、45°和90°三种纤维方向角的单向复合材料板,应用锤击法测试了这三种板前三阶纵向弯曲的固有频率,同时应用ANSYS有限元软件对这三种板进行了模态分析,发现实验值与计算值吻合良好,证明了有限元模型的合理性,应用此有限元模型分析了单向复合材料板前四阶固有频率随纤维方向角的变化情况,得到结论是对于某一阶模态,随着纤维角度的增加,固有频率会随之下降,并且下降的速度会逐渐变缓,这主要是由于随着纤维角度的增加,整体结构的刚度会逐渐降低,导致固有频率的下降;应用应变能法并通过APDL语言编程计算出前四阶模态阻尼损耗因子随纤维角度的变化,并用结构阻尼耗散机理解释了模态阻尼损耗因子的变化曲线,得到的结论是结构整体的阻尼性能主要来自于沿纤维方向的应力σ1、垂直于纤维方向的应力σ2和面内剪切应力τ12的贡献,其中面内剪切应力τ12对整体结构阻尼性能的影响是最大的。

