数方格的策略研究
郑丽君



中图分类号:A 文献标识码:A 文章编号:(2021)-34-494
学生在学习《平行四边形的面积》之前,三年级下册已经学了《面积与面积单位》、《长方形与正方形的面积》。如果说长方形面积公式是所有面积公式的老祖宗,那么平行四边形面积计算公式则起了承上启下的作用。因为这是转化的开始,是学生在“转化”意识驱动下剪拼方法的初次尝试。
若想顺利完成初次转化,一定要牢牢抓住方格的作用。也许有教师会认为数方格是三年级的水平,太简单了,五年级还要数方格吗?不排除有教师会弃之不用。与之相反,我认为,数方格不仅不简单,而且蕴含着大大的道理。
因为面积教学要从数方格开始,借方格理解面积概念,借方格完成转化。
一、方格的重要地位
1、面积单位与方格的关系
人教版三年级下册,在带领学生探索面积单位的过程中,深刻体会到用正方形作为面积单位的合理性,既密铺又利于计算数量的多少。之后教学的1平方厘米、1平方分米、1平方米的大小都用正方形去刻画。所以,在面积教学中,方格和面积单位是紧密结合在一起的。
2、用面积单位度量长方形面积
人教版三年级下册,在探究长方形和正方形面积时,用一个个小方格去摆满长方形,再数出一共有几个小方格,让学生深刻地感受到长方形的面积是用一个个小方格去度量的,如同量长度是用尺子度量一样。所以,作为面积单位的方格,是面积教学中的一把“二维尺子”,可见它的作用不可小觑。
3、借方格唤旧知
人教版五年级上册,在平行四边形面积教学中,再次使用了方格。查阅各版本教材,在平行四边形面积教学中,无不把数方格安排在前面打头阵。数方格在这里起到了两个重要作用,一是对单位面积和面积测量的回忆,这种回忆能为平行四边形的面积计算提供丰富的感性材料,从而使学生获得面积计算的意义支撑;二是对长方形面积公式推导过程的回顾,从直接度量到间接度量,从一维到二维的想象。
二、“不满一格的都按半格计算”合理吗?
数方格对于学生来说不是第一次遇到,但此次数方格与学习长方形面积时数方格不同,这次出现了不完整格。在困难面前,学生要解决的问题是怎样才好数?教材提示,“不满一格的都按半格计算”。这样编写的目的也许是为了帮助学生解决新问题,提供策略指导。但是“不满一格的都按半格计算”这样的规定合理吗?
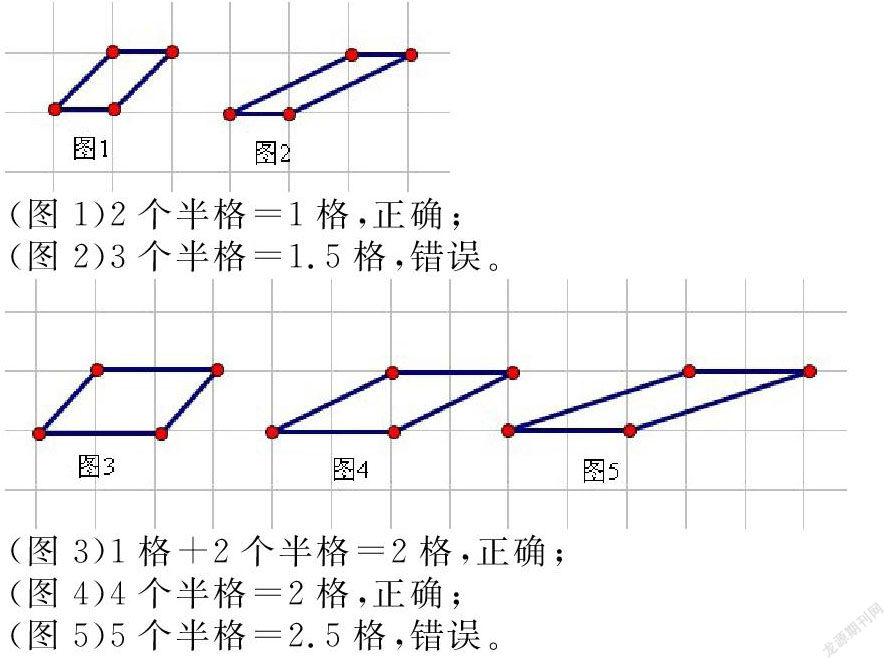
如果都按“不满一格的都按半格计算”的规定去数平行四边形面积会有怎样的结果出现呢?
通过以上面积相同形状不同的平行四边形的对比,我们会发现“不满一格的都按半格计算”这句话是有局限性的。这个规定只有满足以下三个条件才能成立:
1、线段围成的图形。
2、线段的端点都在方格线的交点上。
3、从方格线的交叉点连线段,只要不出现“三分格”即可。(三分格:一个格被线段切割成三部分称为三分格。)
那些不符合的图形都是因为出现了“三分格”。
查阅了不同版本的教材,除了我们使用的人教版外,苏教版教材在编写时也作了这样的规定。但其目的是不一样的。不规则的曲线图,不满格之间是不能直接拼组的。所以,苏教版作这样的规定,既是为学生提供了解决问题的策略,又包含了估算意识的培养。而其他版本都没有这样的规定。
三、数方格再处理
人教版数学五年级上册“平行四边形的面积计算”,教材中呈现让学生通过数方格得出平行四边形的面积,在数的过程中,学生就遇到了难题:有不满半格的或大于半格的怎么办?教材指出“不满一格按半格算”,大多学生不明白为什么不满半格能按半格算。如果不提示,又可以怎么做呢?
教师可以改为提问:谁能用最快的方法数出平行四边形的面积?这就逼着学生先数满格的,再数不满格的,而不满格的那么多,怎么办?这里要留给学生充足的时间,让学生经历困难,通过观察发现,左边的不满格刚好与右边相应的不满格拼成一格,学生通过凑零为整初步感知移拼的转化方法。依据学生思维层次和空间观念的不同,拼的方法和次数各不一样,有的需要拼四次、三次完成,有的两次可以拼成,甚至还可以一次拼成的......
接着,再次引导学生观察整个左边的不满格都可以与右边的不满格拼成满格,拼成后的图形是不规则的,算起来还是不太方便,学生在教师的启发下,进一步发现可以把整个左边的方格移到右边,就可以拼成一个长方形,这样的数方格就是最便捷的方法,学生进一步体验转化的重要意义,同时得出平行四边形的面积=底×高。
这样的铺路引导,学生的探索就有了明确的方法,在不断渗透和体验中,学生对平行四边形转化为长方形的方法有了真正的理解和应用。这一环节既有一定的挑战性,又能充分调动学生已有的知识经验,初显方格魔力。
四、观点与启示
“数方格”这一内容的教学不仅是求面积的一种策略,更重要的是加深了學生对“面积”概念的理解。
而“不满一格按半格计算”的规定,既存在定义上的局限性又约束了学生的探究之路。所以,本人拙见,这个规定应该删去。放手让学生去探究,他们的体会才会更加深刻,数学烙印才会真正烙在他们自己的心里。
——记导演陈蔚

