交通流速度时空二维预测方法

苗成生，刘海鸥

（1.广州汽车集团股份有限公司 汽车工程研究院，广东 广州511434；2.北京理工大学，北京100081）

交通流对车辆导航、自动驾驶车辆的路径和速度规划、交通系统的管控等都有重要作用。准确的交通流预测不仅有助于提高车辆的性能（用于改善规划方法和控制策略等），还可以用于改善车辆、交通控制管理（动态信号灯系统、交通管理系统、公共交通系统和商用车辆操作等），以合理调控交通，提高交通运行效率。

交通信息的预测方法可分为基于模型的预测方法和基于数据的预测方法［1］。基于模型的预测方法是根据交通流模型描述交通的动态变化规律，借助交通模型或仿真软件实现对未来交通的预测［2］。该类方法的重点是搭建准确的交通模型，可分为宏观模型［3］、中观模型［4］、微观模型［5］以及元胞自动机模型［6］等。此外，还有学者通过大量数据库及现有交通数据进行匹配，从数据库中找到适合当前交通特性的数据来预测未来情况［7］。基于模型的预测方法需要具有大量交通数据和先验知识，在使用时也需要进行复杂的数据处理、参数标定以及模型计算，实时应用的难度比较大。与之相比，基于数据的预测方法更快，更容易实现，使用当前和过去的交通数据来直接预测未来的交通状况，不需要使用复杂的交通模型。该类方法根据模型参数可划分为参数化方法和无参方法。参数化方法包含自回归积分移动平均模型（auto-regressive inte⁃grated moving average,ARIMA）及其衍生算法［8-10］、卡尔曼滤波法［11］等。ARIMA方法被普遍应用于时间序列的预测，被视为基本模型，有多个演变模型，如KARIMA（kohonen ARIMA）［8］、SARIMA（season⁃al ARIMA）［9］、VARIMA（vector ARIMA）［10］、STARI⁃MA（space-time ARIMA）［10］等。无参方法包括KNN（k-nearest neighbors）算 法［12］、贝 叶 斯 网 络（bayesian network）［13］、支持向量回归（support vec⁃tor regression,SVR）［14］、神经网络（NN）［15］等。

对交通流预测而言，任何时间和地点的交通状况都与过去在同一地点以及邻近地区的观测结果相关联。交通动态变化过程本质上是一种非线性的时间和空间相关联的变化现象，在自由流动或拥挤的情况下，其动态特性是不同的。对交通流的前期预测方法主要是单维预测模型，如ARIMA、KARIMA、SARIMA、Kalman滤波等，通过目标位置的历史数据和当前数据构成的时间序列建立模型并进行预测，这些方法没有考虑空间特性，是很有局限性的。为此，一些研究人员采用时空模型，如VARIMA、STARIMA、NN等［11,15］，但模型的假设是数据的时空相关性可以通过固定参数来描述。Vlahogianni指出［1］，将基于动态交通网络的交通预测还很不成熟，特别是空间变化特性的研究尚浅。

文中从时间和空间2个维度分析了交通流速度的时空相关特性，提出了交通流速度的时空二维预测模型，基于历史和当前数据，提出了基于递推最小二乘法的动态模型参数识别方法；并将其与所提的车辆宏观运动规划［16］相结合，提出了基于交通流速度预测的车辆宏观运动规划方法。

1 交通流速度时空特性分析

图1为PeMS系统真实交通流速度数据，该系统通过道路的检测设备可提供实时和历史交通数据。分析图1中速度的变化趋势，可得到宏观交通流速度具有以下特性：周期性、地域性、流动性、反馈效应及随机性［17-18］。当前交通流速度受周围交通流速度、历史交通流速度以及随机因素的影响，即交通流速度具有时空相关性。时间维度的相关性，可由自相关函数表征；空间维度的相关性，可由互相关函数表征［18］。

图1 实际道路（US101S）交通流速度

1.1 时间相关性分析

1）检验序列是否为平稳信号 从图1可看出同一位置点的速度序列具有明显的周期性，通过ADF（augmented dickey-fuller）检验，为非平稳信号。选用残差（原始数据与平均值的差值）处理方法对数据进行处理，得到平稳的随机信号。

2）自相关函数和偏相关函数 自相关系数为

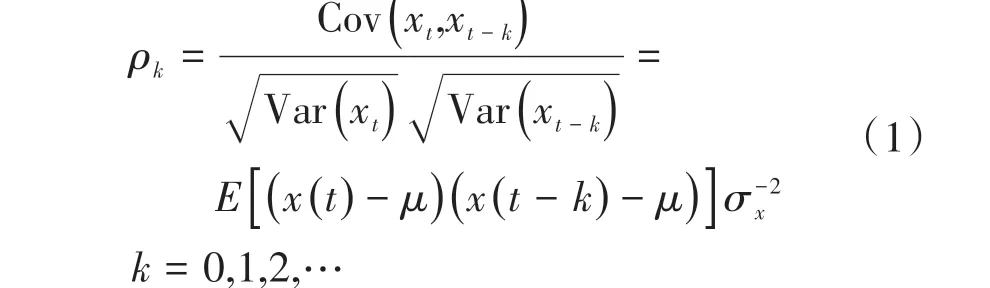
式中：Cov(xt,xt-k)为序列x(t)的滞后时间k的自协方差；Var(xt)为序列x(t)的方差。当k为0时，ρ取1，以k为变量的自相关系数数列ρk称为自相关函数［19］。为进一步分析，计算其偏相关函数：

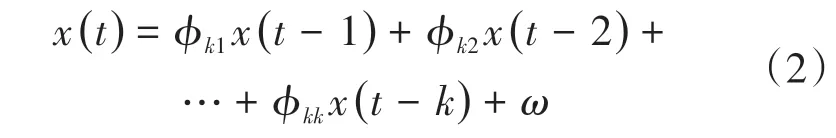
式中：φkj为k阶自回归式中第j个回归系数；ω为随机误差。若把φkk看作滞后阶数k的函数，则φkk为偏相关函数。通过自相关函数（图2a）和偏相关函数（图2b）分析，残差序列具有很强的自相关性，特别是前2个时刻的历史数据。

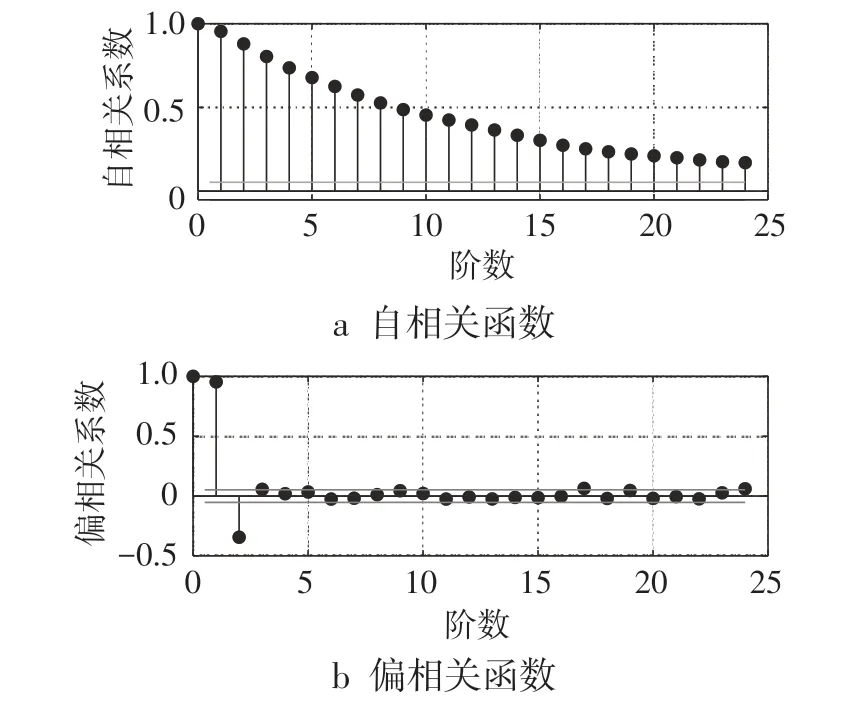
图2 残差序列自相关函数和偏相关函数计算结果

1.2 空间相关性分析

随机信号x(t)和y(t)之间的相关系数为

图3为不同观测点交通流速度的互相关函数，由于互相关函数是偶函数，因此图3只给出了观测点Ⅰ对Ⅱ和观测点Ⅲ对Ⅱ的函数，观测点Ⅱ对Ⅰ和Ⅱ对Ⅲ的函数关于0轴对称。结果显示，当前观测点的速度与邻近观测点的速度也具有较强相关性，特别是当前时刻及其前后2组数据。

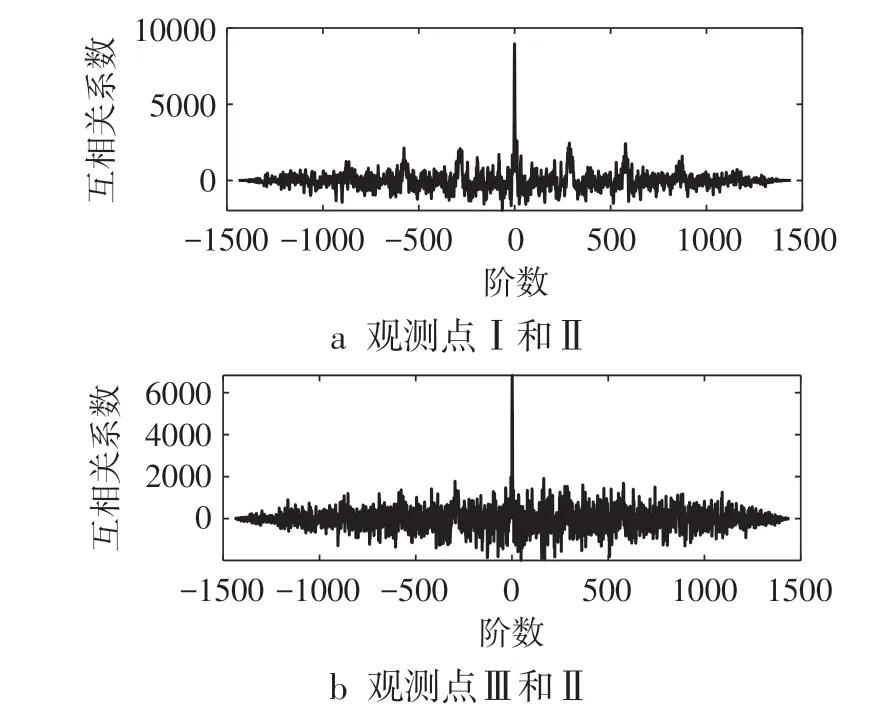
图3 不同观测点交通流速度的互相关函数

2 基于时空相关的交通流速度预测

经上述时空相关性分析，当前观测点交通流速度与历史数据、周围观测点数据相关，利用该特性，可通过当前及周围观测点的当前和历史交通数据对未来的交通流速度进行预测。根据交通流速度的周期性和时空相关性等特性，提出曲线拟合加权预测模型和递推时空二维自回归预测模型相结合的交通流速度时空二维预测方法，交通流速度时空二维预测模型可简化为

式中：s为观测点位置变量；t为时间变量；Y为目标预测值；D为周期性预测结果，由曲线拟合加权预测模型获得，可视为由历史数据得到的基础预测模型；r为残差预测结果，由时空二维自回归预测模型获得，残差序列为原始数据与周期性数据的差值。

实际交通环境中，受地形等因素影响，交通流速度观测设备并没有等距安装。为建立通用性模型，需对实际数据根据位置和时间坐标进行等距化插值处理，插值方法可采用线性插值。

2.1 周期性预测模型

周期性预测模型D(s,t)也称为平均模型：

式中：α为权重系数；T为循环周期，由于工作日的差别，该周期为可变周期，周一到周五为1d，周六和周日为7d；N为历史数据包含的周期数。根据nT（n=1，2，3，…）之前的数据，预测当前的交通流速度。α表示历史数据与当天数据的相似程度，由皮尔森拟合优度衡量［20］，皮尔森拟合优度为

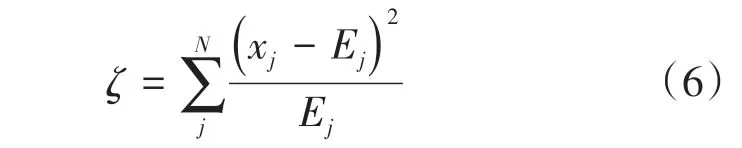
式中：Ej为期望值，即各历史周期内的拟合曲线。由ζ得到权重系数：

文中提出曲线拟合加权预测模型对交通流的周期性进行预测，即先用函数对全天数据进行拟合，得到光滑稳定的曲线，然后利用加权法得到预测模型，既能准确的得到周期性模型，又可以保留原有数列的相关性。交通流速度拟合曲线可由一组基函数f（t）线性组合得到，可以表示为

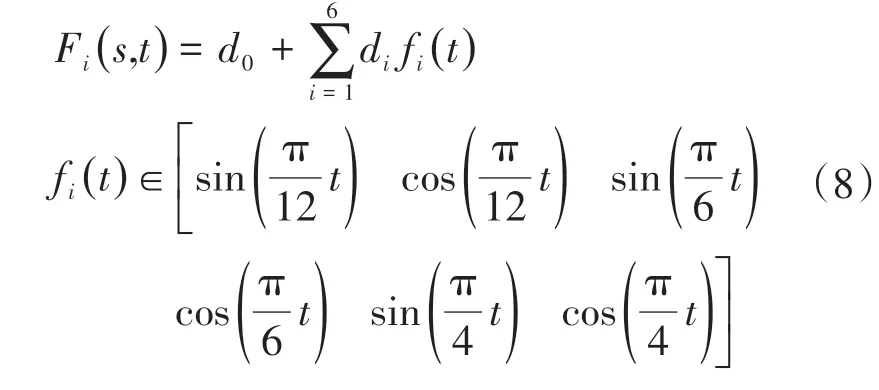
式中：d0,…,d6为待定系数，可由最小二乘法求得。

2.2 递推时空二维自回归预测模型

根据原始数据和拟合值之差得到残差数列，残差数列通过ADF检验，结果为平稳数列。交通流速度残差序列的时空二维自回归预测模型为

式中：m为预测时间步长；Δt为采样时间；Kt为时间相关阶数；Ks为空间相关阶数；Ks为后方交通流相关阶数；K+s为前方交通流相关阶数；αi为后方交通流权重系数；α+i为前方交通流权重系数；a、b为模型参数；e为模型误差定义。

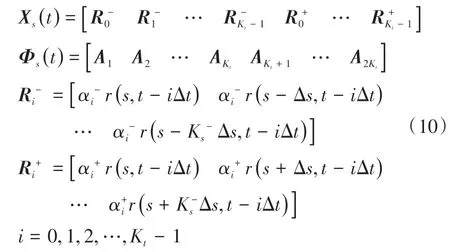
式中：A为对应的待定系数向量。残差预测模型可以简化为

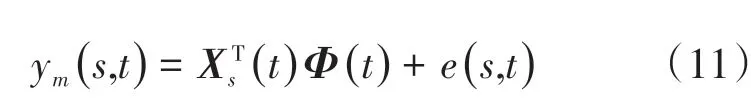
模型参数Φ的估计采用基于递推最小二乘法的自适应参数识别方法。Φ的估计问题可描述为在所研究时间范围内，估计值和实际值的平方差最小。其代价函数J(s)可表示为

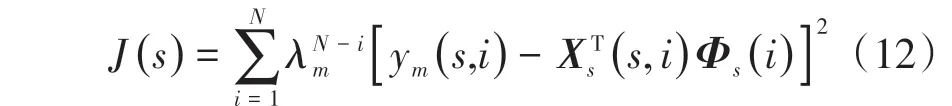
式中：λm为预测模型的遗忘因子，随预测步长的不同，选择不同的遗忘因子。要使式（12）取最小值，应满足J对Φ的偏导数等于0，即

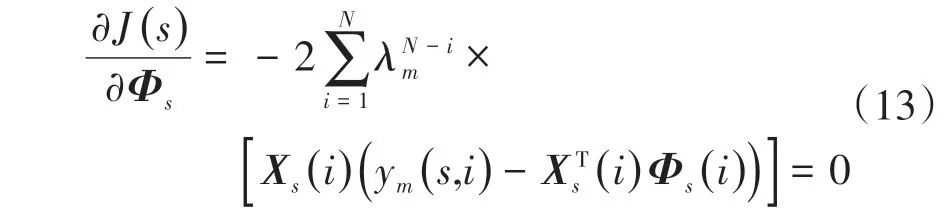
由式（3）可得：

因此第k步的最小二乘参数估计(k)可表示为

则可得到递推最小二乘法参数识别方法［21］：

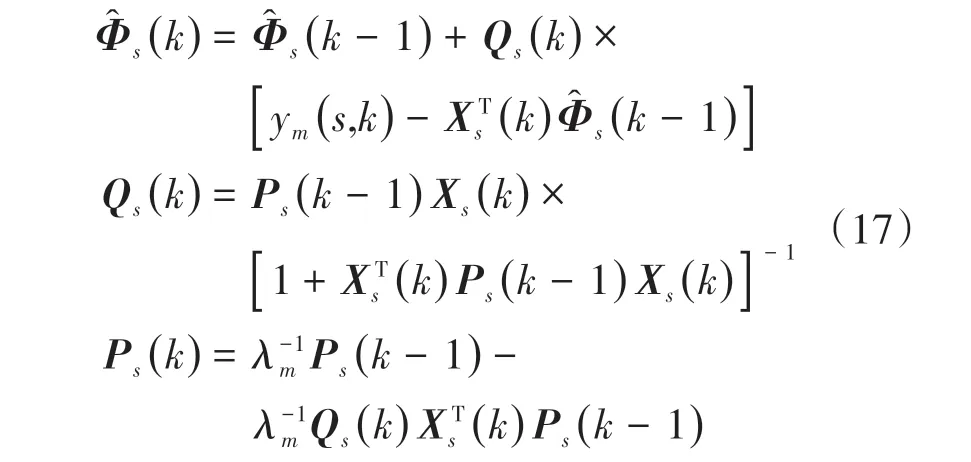
将递推时空二维自回归预测模型的残差预测与曲线拟合加权预测模型结合，得到最终的预测结果。

2.3 静态模型参数的选择

除动态模型参数外，预测误差还受采样时间、时间阶数、空间阶数、权重系数、遗忘因子等影响。

1）采样时间 由PeMS系统得到的数据对应5min采样周期，随着智能交通技术的快速发展，未来智能交通系统的数据采样时间会比现在的采样时间短。为此，考虑对原始采样数据进行插值处理，缩短采样时间。常用的插值方法有线性、临近点、三次样条、多项式插值等，其中，邻近点插值结果为阶跃式，不满足连续变化的要求。其他插值方法的对比结果如图4所示。结果表明，样条插值方法对应的误差最小。插值的结果介于2组原数据之间，该处理方式并不能与实际的动态数据一致，同时也会影响数据的时间、空间相关性，插值的步长应权衡预测误差和真实规律的反应。选择不同的时间步长，结果如图5所示。预测误差基本呈现随着时间步长减小而减小的趋势。当时间步长小于25s后预测误差会随步长减小突然增大，说明插值后的数据影响了交通流动态变化规律，综合考虑选取30s作为时间步长。

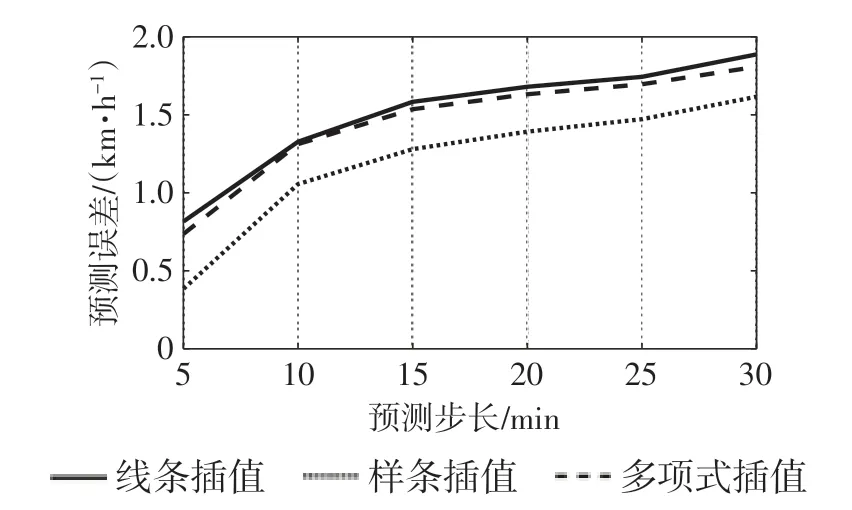
图4 不同差值方法对预测误差的影响

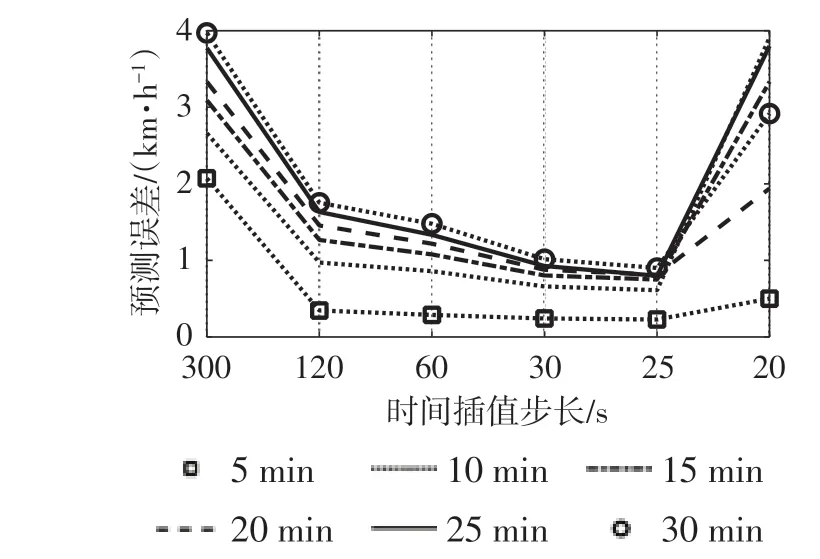
图5 时间差值步长对预测误差的影响

2）正反向交通流数据权重系数 由图1可看出，平均速度以80km·h⁻¹为界限分布在2个区域：

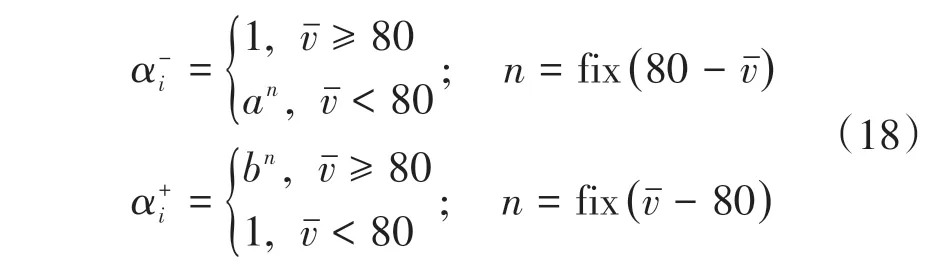
3）时间相关阶数遗忘因子、空间相关参数 分别设置不同的值，对比各参数对预测误差的影响。设置不同的时间相关参数［12345678］，预测误差如图6a所示。当时间相关系数大于4后，预测精度随系数的增大略有减小，但随着系数增多，计算量会增大，因此选择时间相关阶数为4。设置不同的遗忘因子［10.999 0.9950.99 0.980.97 0.96 0.95］，对比结果如图6b所示，最佳遗忘因子为0.98。设定不同的空间相关参数，后向参数设定2、4、…、16，前向参数为1、2、…、10，结果如图6c～d所示。从结果可以得到，最佳空间相关参数分别为10（后）和8（前）。

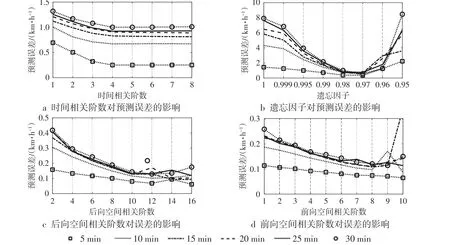
图6 时间相关阶数、遗忘因子、空间相关参数对预测误差的影响

3 基于交通流速度预测的VMMP

车辆宏观运动规划（vehicle macroscopic mo⁃tion planning，VMMP）方法［16］，即根据给定的起点、终点和期望行驶时间，优化得到当前车辆和交通状况下的经济型路线和行驶车速。但优化时使用的是当前时刻的交通数据，而实际交通环境中，交通流速度是个动态变量，不会一直维持当前的状态。而基于当前交通数据的优化结果与车辆实际行驶环境可能出现不完全匹配现象。文中将交通流速度预测与VMMP优化方法相结合，提出基于交通流速度预测的车辆经济型路径和速度协同优化方法，如图7所示。

与文献［16］中优化结构类似，文中优化方法也包含内外2层遗传迭代过程。不同之处在于交通流速度的改变，在速度种群初始化之前增加周期性速度预测。并将其运用到S5和S6中。由于时空二维预测模型计算量较大，此处只利用周期性预测模型进行初步预测，以提高计算效率。同时在路径下次迭代之前，增加预选和Jr二次评估过程，如图7中S8～S11所示。首先，根据Jr（图7中S7）的初始值，初选Jr较小的个体。然后，利用时空二维速度预测模型对所选个体路径的速度进行预测Vpre，将预测结果与优化的速度进行对比，如果优化速度超出预测速度，则将超出的速度替换为预测值，计算新速度向量对应的Jr，并取代原来的Jr作为路径的评价函数值，其他说明可参考文献［16］。图7中，S12的终止条件为

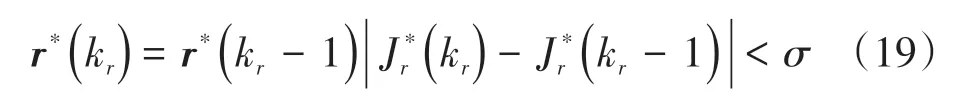
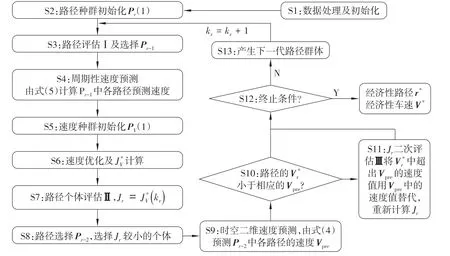
图7 基于交通流速度预测的VMMP方法

4 实验及仿真结果分析

4.1 周期性预测模型结果分析

有些相关研究中，周期性预测模型常采用平均值法，如前1～4d的数据平均，预测当前的平均速度。该方法稳定性较差，当其中某天情况与其他差别较大时，对预测结果会产生较大的影响，且对残差数列的相关性产生影响。图8为速度拟合曲线和周期性预测结果。

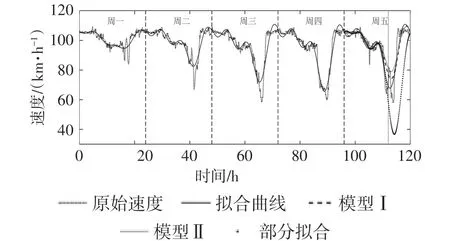
图8 速度拟合曲线和周期性预测结果

模型Ⅰ为所提曲线拟合加权预测模型，模型Ⅱ为常用的平均模型，均由周一至周四的拟合曲线得到；拟合曲线为全天数据计算得到的；部分拟合曲线是96～112h（周五）的数据拟合得到的。其中，周一至周四的权重系数由式（6）～（7）计算得到［0.11,0.19 ,0.30 ,0.40 ］。由图8中曲线也可直观看出周三和周四的曲线与周五的相似度更高，与计算的权重系数相吻合。对比实际拟合曲线、模型Ⅰ和Ⅱ的曲线，可以得出所提出的曲线拟合加权预测模型更接近实际拟合曲线。在实际应用中，假设当前时刻为112h，112～120h数据未知，则由部分数据得到的拟合曲线与实际值偏差较大。相比之下，文中所提的曲线拟合加权预测模型更准确。

4.2 时空相关性的交通流速度预测模型结果分析

图9为部分预测结果及误差曲线，单步预测的步长为5min，多步预测的步长为30min。预测结果与实际值能较好地吻合，单步预测误差能控制在5km·h⁻¹内，多步预测误差可保证绝大部分时刻在5km·h⁻¹内。单步和多步预测误差绝对值的平均值分别0.58 km·h⁻¹和1.00 km·h⁻¹。由此可得，预测误差会随着预测步长的增加而增大。

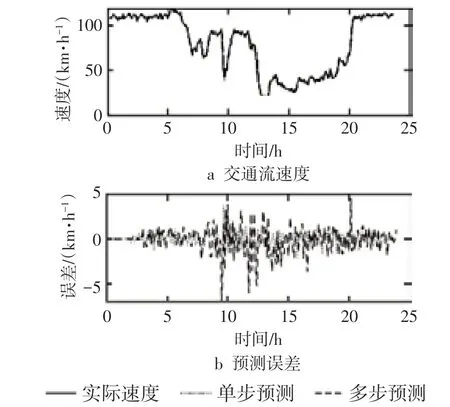
图9 交通流速度预测结果

4.3 基于PeMS系统真实交通流数据的仿真分析

文中选取了PeMS系统不同路段（约15条路包含2个方向）、不同时间（1年内）的真实数据。图10为圣地亚哥的部分路段结果，图10a为真实地图信息（谷歌地图获得），图10b为简化后的SUMO仿真地图。O为给定的起点，D为给定的终点。由于PeMS系统只提供了高速公路的数据信息，SUMO模型中只保留了高速公路和部分主要干道的信息。

图10 圣地亚哥交通仿真模型

由于工作时间的影响，路段L处呈现规律性的交通阻塞现象。研究固定路线下的预测速度对油耗的影响，即给定OD（图10）和路径RI。无交通阻塞情况下，该路径的最短行驶时间为16min。从实际交通数据中选取1段较特殊的数据，即车辆行驶至位置O时，道路顺畅，无交通阻塞现象，但3min后在路段L处会出现交通拥堵现象。给定期望行驶时间为24min，仿真结果如表1所示。其中，TE为期望行驶时间，TS为仿真时间，ΔF为各组油耗相比于未优化车速（表1中的G-Ⅰ）下的增（减）量，G-Ⅰ、G-Ⅱ和G-Ⅲ分别表示最快路径（未优化）结果、当前交通流速度下的优化结果和预测交通流速度下的优化结果。表1中结果显示：1）G-Ⅰ组对应的行驶时间最短，G-Ⅱ和G-Ⅲ组对应时间较长，但都小于期望行驶时间；2）G-Ⅰ组对应的油耗最高，G-Ⅱ和G-Ⅲ均能降低油耗，G-Ⅲ的效果更加明显。因此在满足期望时间条件下，基于交通流速度预测的速度优化可进一步改善车辆燃油经济性。

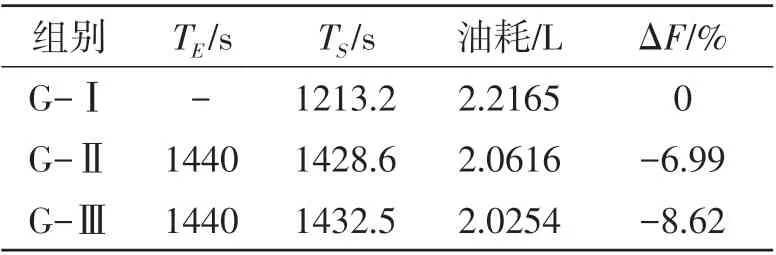
表1 路线RI不同行驶速度下的车辆行驶油耗

为进一步研究交通流速度预测对车辆宏观运动规划的影响，将路径也作为优化变量。当前交通流速度（行驶至O位置）下，最快行驶路径依然是RI，但经济型行驶路线有所改变，具体结果如表2所示。G-Ⅰ和G-Ⅱ分别表示最快路径（未优化）结果和基于当期交通流速度的优化结果；G-Ⅲ和G-Ⅳ分别表示1.5 TE和1.75TE期望行驶时间下的基于交通流速度预测的优化结果。表2中结果显示：1）基于当期交通流速度和预测交通流速度下的经济型路径不同，如G-Ⅱ和G-Ⅲ组结果所示；2）G-Ⅱ、G-Ⅲ和G-Ⅳ的行驶时间均能满足期望时间约束；3）与G-Ⅱ优化结果相比G-Ⅲ和G-Ⅳ能更大程度地改善车辆燃油经济性。因此，考虑交通流速度预测的车辆宏观运动规划与当前交通流速度下的规划相比，可进一步改善车辆的燃油经济性。

表2 车辆行驶油耗对比

5 结论

文中研究了交通流速度的周期性和时空相关性，提出了二维交通流速度预测模型，由曲线拟合加权预测模型和时空二维自回归预测模型组成。经实际交通数据验证，文中预测方法能准确预测未来交通流速度，可实现不同步长的预测。仿真结果表明，基于速度预测的车辆运动规划模型可预测未来交通的变化，进一步提高了车辆燃油经济性。文中预测模型不仅可以用于宏观运动规划，提高车辆燃油经济性，还可以用于交通管理系统以及车辆动力传动系统的实时控制。